Способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения

Способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано для определения и коррекции радиальной дисторсии оптических подсистем видеокамер и систем технического зрения, использующих в качестве приемников изображения матричные приемники изображения.

Известен способ калибровки видеокамеры, входящей в систему технического зрения [R.Y. Tsai. "A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses", IEEE Trans. Rob. Autom, RA-3(4), pp.323-344, 1987; George S.K. Fung, Nelson H.C. Yung, Grantham K.H. Pang, "Camera calibration from road lane markings", The university of Hong Kong department of electrical and electronic engineering. Opt. Eng, 42(10), pp.2967-2977, 2003 (стр.2968, 2 колонка, первый абзац)], позволяющий по изображению эталонного калибровочного объекта на ряду с другими параметрами определять радиальную дисторсию линз оптической подсистемы. Недостатком способа является использование при калибровке калибровочного объекта, состоящего из калибровочных точек - вершин 16 черных квадратов, расположенных на светлом фоне, исключающее проведение калибровки в случае невозможности размещения калибровочного объекта на рабочей сцене и исключающее проведение адаптивной калибровки (т.е. когда необходимость проведения калибровки вызвана какими-либо изменениями в системе технического зрения (СТЗ)), например, с целью "приблизить" наблюдаемый объект необходимо изменить фокусное расстояние оптической подсистемы (при оснащении СТЗ трансфокатором - устройством, изменяющим фокусное расстояние оптической подсистемы и, как следствие, изменяющим угол просмотра ("увеличение")).

Наиболее близким является способ калибровки лазерной системы технического зрения [Vark Reeves, Andrew J. Moore, Duncan P. Hand, Julian D.C. Jones. "Dynamic shape measurement system for laser materials processing", Opt. Eng. 42(10), pp.2923-2929, 2003 (стр.2925, последний абзац)], согласно которому наряду с другими параметрами калибровки определяется радиальная дисторсия и заключающийся в расположении калибровочной плоскости в n+1 параллельных позициях, проецировании на калибровочную плоскость интерференционной картины и последующем определении параметров калибровки. Недостатком способа является использование лазера для проецирования и многократное расположение калибровочных плоскостей в параллельных позициях, исключающее применение способа в случаях, когда приведенное выше расположение калибровочной плоскости невозможно или затруднено, например, в системах слежения за дорожным движением.

Технической задачей изобретения является калибровка радиальной дисторсии оптической подсистемы системы технического зрения без использования специально созданного калибровочного объекта, калибровочный объект выбирается из объектов рабочей сцены.

Техническая задача решается тем, что в известный способ калибровки активной системы технического зрения, включающий ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле

где k₁, k₂,... - коэффициенты радиальной дисторсии, r_a=(х_a ²+y_a ²)^1/2 - радиальное расстояние, (Δх_ra, Δy_ra) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии радиальной дисторсии, согласно изобретению выделяют контура и бинаризируют изображение, выбирают калибровочный объект из объектов рабочей сцены на основе математического аппарата нечеткой логики, определяют координаты центральной точки калибровочного объекта как среднее арифметическое координат всех точек объекта, позиционируют видеокамеру СТЗ в n разных направлениях наблюдения при постоянно находящемся в кадре калибровочном объекте, определяют координаты центральной точки калибровочного объекта на изображении для n разных направлений наблюдения и определяют коэффициенты радиальной дисторсии.

Изобретение может быть использовано для калибровки радиальной дисторсии систем технического зрения, широко применяемых для контроля различных автоматизированных процессов промышленности, автоматизированного слежения за дорожным движением, а также для калибровки радиальной дисторсии при производстве фото- и видеокамер с матричными приемниками изображения и соответствует критерию "промышленная применимость".

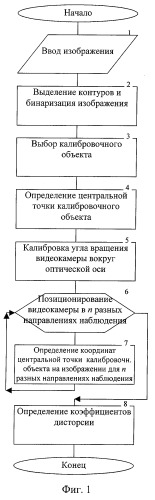
Сущность изобретения поясняется чертежами, где на фиг.1 - блок-схема алгоритма калибровки радиальной дисторсии, фиг.2 изображает процесс определения угла вращения камеры вокруг оптической оси, фиг.3 поясняет идентификацию калибровочного объекта до и после смещения направления наблюдения видеокамеры, на фиг.4 показана декартова система координат, используемая при определении координат точки на изображении, а также пояснение к способу определения радиальной дисторсии.

Предлагаемый способ позволяет калибровать радиальную дисторсию оптической подсистемы СТЗ путем определения коэффициентов k₁, k₂,... выражения (1). Согласно [Vark Reeves, Andrew J. Moore, Duncan P. Hand, Julian D.C. Jones. "Dynamic shape measurement system for laser materials processing", Opt. Eng. 42(10), pp.2923-2929, 2003 (стр.2926, текст между 4 и 5 формулами)], для практического применения достаточно определять только коэффициент k₁, однако разработанный способ позволяет, при необходимости, определять и последующие коэффициенты ряда k₂,....

Блок-схема алгоритма процесса калибровки представлена на фиг.1.

В блоке 1 (фиг.1) производится ввод изображения в ЭВМ. Ввод может быть произведен с помощью серийно выпускаемых устройств ввода видеосигнала в ПЭВМ, например с помощью видеокарты фирмы Nvidia типа "GeForce" с видеовходом, или другими устройствами, входящими в комплект видеокамеры или фотоаппарата, например по шине USB. Под изображением будем понимать матрицу значений яркостей пикселов оцифрованного изображения

где х, y - координаты пиксела изображения по горизонтали и вертикали, соответственно, x∈[-X/2; X/2], y∈[-Y/2; Y/2], X, Y - размерность изображения по горизонтали и вертикали, соответственно

В блоке 2 (фиг.1) производится выделение контуров объектов на изображении стандартным оператором, например оператором Лапласа [Методы компьютерной обработки изображений /Под. Ред. В.А. Сойфера. - М.: Физматлит, 2001] и бинаризация. Согласно оператору Лапласа вычисляются вторые производные функции яркости Ι_˜(х,y) по горизонтальному и вертикальному направлениям изображения

В случае дискретной функции яркости Ι(х, y) вторые производные аппроксимируются вторыми разностями и оператор определения контура в точке с координатами (х, у) записывается [Методы компьютерной обработки изображений /Под. Ред. В.А. Сойфера. - М.: Физматлит, 2001]

где G(x,y)=|Ι(x+1,y)+Ι(x-1,y)+Ι(x,y+1)+Ι(х,у-1)-4·Ι(х,у)|,

Β - контурное изображение, определяемое множеством значений яркостей в точках с координатами (х,у),

L_p - пороговое значение изменения яркости, по которому определяется принадлежность точки изображения фону или контуру.

Порог L_p рассчитывается по формуле

где G_min - параметр, определяющий минимальное изменение яркости и задаваемый для всего изображения:

После выделения контуров осуществляется переход к выбору калибровочного объекта. В блоке 3 (фиг.1) производится выбор калибровочного объекта из объектов рабочей сцены на основе математического аппарата нечеткой логики [Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях: Монография. Тюмень: Издательство Тюменского государственного университета, 2000].

Введем лингвистическую переменную (ЛП) "калибровочный объект" для выбора калибровочного объекта из множества объектов на изображении. Калибровочный объект должен удовлетворять следующим условиям:

- иметь оптимальную площадь и размер, определяемый размером описанного вокруг объекта прямоугольника;

- находиться на оптимальном расстоянии от края кадра изображения;

- не изменяться в течение определенного промежутка времени (позволяет отделить изменяющиеся во времени объекты от

статичных).

Функция принадлежности ЛП "калибровочный объект" μ_кк равна

где μ_s - функция принадлежности терму "оптимальная площадь",

μ_w - функция принадлежности терму "оптимальное окно",

μ_kf - функция принадлежности терму "оптимальное положение в кадре",

μ_t - функция принадлежности терму "неподвижный объект".

Функция принадлежности μ_s терма "оптимальная площадь", зависящая от площади контура S, равна

где N_kl - количество точек объекта.

Функция принадлежности μ_w терма "оптимальное окно" определяется размерами по горизонтали и вертикали описанного вокруг объекта прямоугольника

W_x, W_y - размеры описанного прямоугольника по горизонтали и вертикали, соответственно, параметры a, b подобраны экспериментально.

Функция принадлежности μ_kf терма "оптимальное положение в кадре" позволяет выбрать контура, расположенные близко к краю кадра, и равна

(х, у) - координаты центра описанного прямоугольника, параметры а, b подобраны экспериментально.

Функция принадлежности μ_t терма "неподвижный объект" позволяет отделить статичные объекты от динамических

ΔК - количество несовпадающих точек объекта через определенный промежуток времени, выбранный в результате экспериментальных исследований равным 1 с.

В блоке 4 (фиг.1) производится определение центральной точки (ЦТ) калибровочного объекта. В качестве ЦТ выбирается точка кадра, являющаяся центром тяжести [Дегтярев С.В., Садыков С.С., Тевс С.С., Ширабакина Т.А. Методы цифровой обработки изображений: Учебное пособие. Ч.1/Курск. Гос. Техн. Ун-т. Курск, 2001] изображения калибровочного объекта и определяемая средними координатами всех точек калибровочного объекта по горизонтали и вертикали.

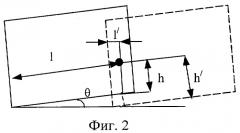
В блоке 5 (фиг.1) угол вращения видеокамеры вокруг оптической оси калибруется путем смещения направления наблюдения видеокамеры в горизонтальной плоскости и последующего определения угла (фиг.2) по двумерным координатам на плоскости изображения ЦТ до и после смещения направления наблюдения видеокамеры.

Определение угла θ основано на том, что высота h ЦТ в кадре, измеренного от нижней границы кадра, не будет совпадать с высотой h', измеренной при смещении направления наблюдения видеокамеры в ту или иную сторону по горизонтали (фиг.2, высоты h и h' не равны), в случае, если угол ≠0.

При этом угол вычисляется по формуле

где l, l' - расстояния от левого края кадра до ЦТ, выраженные в пикселях,

h, h' - высоты от нижнего края кадра до ЦТ, выраженные в пикселях.

В блоке 6 (фиг.1) производится последовательное ориентирование видеокамеры в n направлениях наблюдения, так чтобы калибровочный объект всегда находился в кадре. При этом для идентификации калибровочного объекта после смещения введена ЛП "идентичность смещенного объекта"

где μ_ид - функция принадлежности терма "идентичность объекта",

μ_n - функция принадлежности терма "ожидаемое положение", характеризующая полученное положение калибровочного объекта после смещения и ожидаемое положение калибровочного объекта.

Для описания объекта Κ_l строится множество векторов ν_ij с i-й точки Т_i(x_i,y_i) объекта на j-ю точку Т_j(x_j,y_i) этого же объекта

где d_ij - расстояние между точками T_i, и T_j,

α_ij - направление с i-й точки объекта на j-ю точку.

Расстояние d_ij определяется как

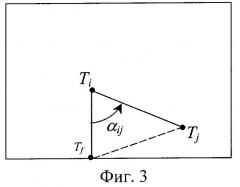
Углом с i-й точки объекта на j-ю точку считается угол между вертикальной осью кадра и направлением на j-ю точку (фиг.3). По теореме косинусов из треугольника ΔT_fT_iT_j

Функция принадлежности терма "идентичность объекта" μ_ид определяется как идентичность расстояний d_ij между i-й j-й точками и идентичность углов α_ij-

где

- разность расстояний между точками до смещения и после смещения в пикселах,

- разность величин углов между точками до смещения и после смещения в радианах.

Функция принадлежности μ_n терма "ожидаемое положение" характеризуется разностью ожидаемого и фактического положения калибровочного объекта

где - предполагаемое среднее значение горизонтальных координат множества составляющих объект точек,

- фактическое среднее значение горизонтальных координат множества составляющих объект точек, рассчитываемое на основе априорной информации об угловой скорости смещения направления наблюдения и времени смещения или на основе апостериорного определения угловой скорости при смещении на 1 пиксель и последующего расчета по формуле

где V_x - скорость смещения в пикселях в секунду (которая может быть известна или определена каким-либо способом),

t - время смещения.

В блоке 7 (фиг.1) производится определение координат (х', y') ЦТ на изображении после каждого изменения направления наблюдения. В блоке 8 (фиг.1) производится определение радиальной дисторсии, путем решения системы уравнений и определения коэффициентов радиальной дисторсии.

Рассмотрим определение коэффициента радиальной дисторсии с учетом того, что для практического применения достаточно определять только коэффициент k₁. Формула (1) преобразуется к виду

Разности Δx_r, Δy_r между измеренными координатами точки по горизонтали х' и вертикали у' и их истинными координатами х по горизонтали и у по вертикали соответственно равны

Δx_r=х'-х,

Δy_r=y'-y.

После подстановки разностей Δx_r, Δy_r в (23) получаем систему

в которой три неизвестных (х, у, k₁) и два уравнения.

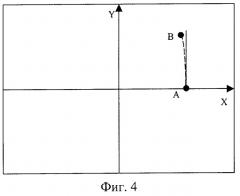
Сориентируем видеокамеру так, чтобы ЦТ занимала на изображении положение А (фиг.4), характеризующееся равенством ординаты точки нулю. Затем сместим направление наблюдения в вертикальной плоскости так, чтобы ЦТ занимала положение В, при этом истинные абсциссы точек А и В равны. Составим систему уравнений, используя определенные по изображению координаты точек А(х_А,у_А) и B(x_В,у_В) и выражения (23), (24)

Система (25) состоит из 4 уравнений, 4 неизвестных (х_А, x_В, у_В, k₁) и, с учетом принадлежности абсцисс и ординат точек лежащей внутри фотоприемной матрицы области х∈[-Х/2; Х/2], y∈[-Y/2; Y/2], имеет единственное решение. Система может быть решена одним из известных численных методов на ЭВМ.

При недостаточной для какой-либо задачи точности определения радиальной дисторсии по коэффициенту k₁ точность может быть повышена путем определения дополнительных коэффициентов k₂...k_2+m. Для этого после получения координат точки В продолжается смещение видеокамеры в вертикальном направлении вверх или вниз для получения координат m дополнительных точек. При этом в систему (25) дополнительно вводятся по два аналогичных второму и третьему уравнениям системы (25) уравнения на каждую дополнительную точку и два новых неизвестных (k_i и y_i). Первое уравнение системы (25) изменяется в соответствии с выражением (1).

Точность определения коэффициента k₁ может быть повышена путем определения коэффициентов k_1p no p парам точек А и В (т.е. ЦТ единственная, а видеокамера смещается так, чтобы образовалось несколько пар А и В) и последующего усреднения коэффициентов k_1p. Аналогично может быть повышена точность определения дополнительных коэффициентов k₂...k_2+m.

При определении радиальной дисторсии наряду со смещением направления наблюдения видеокамеры в вертикальной плоскости может использоваться смещение в горизонтальной плоскости.

Изобретение позволяет определять радиальную дисторсию оптических подсистем видеокамер, цифровых фотокамер и систем технического зрения, использующих в качестве приемников изображения матричные приемники изображения без использования специального калибровочного объекта в автоматическом режиме, благодаря чему калибровка радиальной дисторсии может производится адаптивно - по мере необходимости, вызванной какими-либо причинами, например изменениями в системе технического зрения, оснащенной трансфокатором, - с целью "приблизить" наблюдаемый объект необходимо изменить фокусное расстояние оптической подсистемы.

Способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения, включающий ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле

где k₁, k₂,... - коэффициенты радиальной дисторсии, радиальное расстояние, (Δх_ra, Δy_ra) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии дисторсии, отличающийся тем, что дополнительно выделяют контуры и бинаризируют изображение, выбирают калибровочный объект из объектов рабочей сцены на основе математического аппарата нечеткой логики, определяют центральную точку калибровочного объекта как среднее арифметическое всех точек объекта, позиционируют видеокамеру СТЗ в n разных направлениях наблюдения при постоянно находящемся в кадре калибровочном объекте, определяют координаты центральной точки калибровочного объекта на изображении для n разных направлений наблюдения и определяют коэффициенты радиальной дисторсии.