Способ преобразования кода системы остаточных классов в напряжение

Способ преобразования кода системы остаточных классов в напряжение

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматики и вычислительной техники и может быть использовано при проектировании устройств преобразования цифрового кода числа А в системе остаточных классов (СОК) в напряжение в блоках сопряжения разнотипных элементов вычислительных и информационно-измерительных систем.

Известен способ (аналог) преобразования кода СОК в напряжение [1, с.239-240], заключающийся в преобразовании кода числа в СОК в позиционную систему счисления (ПСС) и последующем формировании из полученного позиционного кода напряжения путем суммирования токов, прямо пропорциональных весам разрядов позиционного кода, на общем сопротивлении нагрузки [2, с.208-211].

Недостаток способа - низкое быстродействие, обусловленное необходимостью дополнительного преобразования кода СОК в ПСС.

Известен также способ (аналог), базирующийся на алгоритме преобразования позиционного кода числа А из его кода (α₁, α₂, ..., α_N) в СОК в соответствии с китайской теоремой об остатках [1, с.31; 3, с.35-39, с.77-78]:

где [•] - целая часть числа; m_i - совокупность взаимно простых целых положительных чисел; μ_i - вес ортогонального базиса, получаемый из решения сравнения (μ_iM_i)modm_i≡1; r_A - ранг числа А, представляющий собой целое неотрицательное число, показывающее, во сколько раз диапазон СОК - М был превзойден при переходе от представления числа в СОК к его позиционному представлению.

Данный способ преобразования кода СОК в напряжение заключается [4, с.23-24] в вычислении по модулям m_i произведений разрядов α_i кода числа А в СОК на веса ортогональных базисов μ_i этих разрядов - β_i=(α_iμ_i)modm_i, где m_i - основания СОК; i=1, 2, ... N, суммировании на общем сопротивлении нагрузки токов, прямо пропорциональных значениям дроби β_i/m_i, и вычитании из напряжения, полученного в результате прохождения суммы этих токов через сопротивление нагрузки, напряжения, прямо пропорционального рангу числа - r_A.

Недостаток аналога - низкое быстродействие, так как при преобразовании кода СОК в напряжение необходимо рассчитывать ранг числа - r_A. Известные алгоритмы получения ранга числа [3, с.78-82; 4, с.23-24] требуют дополнительных затрат оборудования и выполняется только за N шагов, где N - число оснований в СОК.

Наиболее близким по технической сущности (прототипом к предлагаемому изобретению) является способ [5], включающий вычисление по модулям m_i произведений разрядов α_i кода числа А в СОК на веса ортогональных базисов μ_i этих разрядов - β_i=(α_iμ_i)modm_i, где m_i - основания СОК; i=1, 2, ... N, формирование опорного гармонического колебания u₀(t)=Ucos(ω·t), где U и ω - соответственно амплитуда и частота гармонического колебания; t - время, получение из опорного колебания u₀(t) двух гармонических колебаний u₁(t) и u₂(t) соответственно путем N сдвигов фазы на , где i=1, 2, ... N, и сдвига фазы на π/2 и определение интеграла произведения этих колебаний: , где Т_u - интервал интегрирования, причем значение u_u при U²T=M/π, Т_u>(2...3)T и 0≤A≪M, где Т - период гармонического колебания, равно величине числа А.

Недостаток прототипа заключается в том, что требуемая точность преобразования достигается только при значительном (в десятки раз) превышении диапазона разрядной сетки СОК - относительно возможного диапазона изменения преобразуемого числа А. В связи с этим в арифметические устройства, функционирующие в СОК, для расширения диапазона разрядной сетки необходимо вводить дополнительные основания m_i, что, в свою очередь, приводит к увеличению аппаратурных затрат вычислительных устройств.

Целью заявляемого способа является увеличение диапазона изменения преобразуемой величины А, в пределах которого достигается приемлемая точность преобразования.

Технический результат выражается в повышении точности преобразования кода СОК в напряжение.

Поставленная цель достигается тем, что в известном способе, включающем вычисление по модулям m_i произведений разрядов α_i кода числа А в СОК на веса ортогональных базисов μ_i этих разрядов - β_i=(α_iμ_i)modm_i, где m_i - основания СОК; i=1, 2, ... N, формирование опорного гармонического колебания u₀(t)=Ucos(ω·t), где U и ω - соответственно амплитуда и частота гармонического колебания; t - время, согласно изобретению из опорного колебания u₀(t) формируют гармоническое колебание u₀₁(t) путем L сдвигов фазы на угол , и гармоническое колебание u₀₂(t) путем сдвига фазы на угол π/2 и (N-L) сдвигов фазы на угол , где j=1, 2, ... L; L - целая часть результата деления числа N на 2; k=(L+1), (L+2), ... N, гармоническое колебание u₀₁(t) подвергают детектированию в балансном фазовом детекторе, а в качестве опорного сигнала фазового детектора используют гармоническое колебание u₀₂(t), амплитуду которого устанавливают в два раза меньше, чем амплитуду гармонического колебания u₀₁(t), причем выходное напряжение балансного фазового детектора при - М/4<А<М/4, где - диапазон разрядной сетки СОК, с погрешностью, не превышающей 10%, прямо пропорционально величине числа A.

Сущность изобретения основывается на использовании свойства периодичности гармонической функции и утверждении китайской теоремы об остатках.

Известно, что

где р=1, 2, 3, ...

Пусть формируются два гармонических колебания u₁(t)=U₁cos(ωt) и u₂(t)=U₂sin(ωt) с амплитудой U и частотой ω.

Если начальную фазу гармонического колебания u₁(t) сдвинуть L раз на величину , где L - целая часть результата деления числа N на 2; j=1, 2, ... L, а начальную фазу второго гармонического колебания u₂(t) сдвинуть (N-L) раз на величину , где k=(L+1), (L+2), ... N, то после этих сдвигов данные гармонические колебания будут описываться соответствующими выражениями:

Так как

а в свою очередь

то на основании (3) и (5) получим

Аналогично, с учетом выражения (4) получаем формулу

второе слагаемое в которой преобразуется к виду

Соответственно, на основании (4) и (7) получаем

He трудно показать, что в соответствии с китайской теоремой об остатках разность фаз гармонических колебаний (6) и (8) будет прямо пропорциональна величине числа А, код в СОК которого равен (α₁, α₂, ..., α_N):

Для получения напряжения, прямо пропорционального величине сдвига фаз (9), может быть применен балансный фазовый детектор [6, с.142, рис.7.29]. Пусть в таком фазовом детекторе на его сигнальный вход поступает гармоническое колебание (6):

сформированное из колебания u₀(t) путем L сдвигов фазы на угол , j=1, 2, ... L, а в качестве опорного сигнала используется гармоническое колебание (8):

сформированное из колебания u₀(t) путем сдвига фазы на π/2 и (N-L) сдвигов фазы на угол , k=(L+1), (L+2), ... N.

С учетом (9), (10) и (11) выходное напряжение в балансном фазовом детекторе образуется как разность огибающих результирующих колебаний на диодах Д₁ и Д₂ амплитудных детекторов в составе данного фазового детектора [6, с.142-143, рис.7.29]:

где К_PhD - коэффициент передачи фазового детектора.

При U₂=U₁/2 получаем:

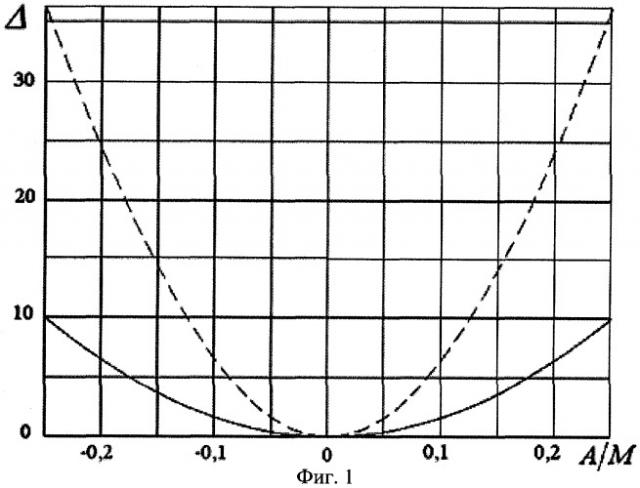
Зависимость выходного напряжения балансного фазового детектора (12) при таком соотношении амплитуд сигнального и опорного колебания оказывается близкой к линейной зависимости на интервале - М/4<А<М/4 с погрешностью, не превышающей 10%. В качестве иллюстрации этого на фиг.1 приведен в виде непрерывной линии график относительного отклонения выходного напряжения (12) от линейной зависимости - Δ, выраженный в процентах, который построен по следующей формуле:

Здесь же штриховой линией представлен график относительного отклонения выходного напряжения прототипа [5] - от линейной зависимости, выраженный в процентах, который построен по следующей формуле:

Из приведенных графиков видно, что по сравнению с прототипом предлагаемый способ обеспечивает большую точность преобразования кода системы остаточных классов в напряжение в более широком диапазоне изменения преобразуемой величины А.

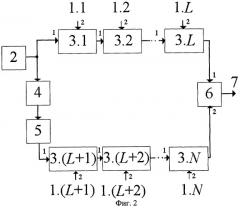
На фиг.2 приведена структурная схема устройства, реализующего предлагаемый способ преобразования кода СОК в напряжение, где 1.1-1.N - информационные входы устройства, 2 - генератор гармонического колебания, 3.1-3.N - управляемые фазовращатели, 4 - фазовращатель на угол , 5 - аттенюатор, 6 - балансный фазовый детектор, 7 - выход устройства.

Информационные входы 1.1-1.N соединены с вторыми входами соответствующих управляемых фазовращателей 3.1-3.N, при этом выход генератора гармонического колебания 2 соединен непосредственно с первым входом управляемого фазовращателя 3.1 и через фазовращатель на угол 4 и аттенюатор 5 - с первым входом управляемого фазовращателя 3.(L+1), причем выход управляемого фазовращателя 3.j соединен с первым входом управляемого фазовращателя 3.(j+1), где j=1, 2, ... L-1, а выход управляемого фазовращателя 3.р соединен с первым входом управляемого фазовращателя 3.(р+1), где p=L+1,L+2,...N-1, при этом выход управляемого фазовращателя 3.L подключен к первому входу балансного фазового детектора 6, второй вход которого соединен с выходом управляемого фазовращателя 3.N, причем выход балансного фазового детектора 6 является выходом 7 устройства.

Рассмотрим работу устройства.

На N информационных входов 1.1-1.N устройства поступают коды α_i соответствующих разрядов числа А в СОК, где i=1,2,...N. В соответствии с этими кодами в управляемых фазовращателях 3.1-3.L устанавливаются сдвиги фазы на угол , где β_j=(α_jμ_j)modm_j;j=1, 2, ... L; L - целая часть результата деления числа N на 2, а в управляемых фазовращателях 3.(L+1)-3.N устанавливаются сдвиги фазы на угол , где β_p=(α_pμ_p)modm_p; p=(L+1), (L+2), ... N.

После прохождения гармонического колебания u₀(t)=Ucos(ω·t) с выхода генератора 2 через управляемые фазовращатели 3.1-3.L на выходе управляемого фазовращателя 3.L устанавливается суммарный набег фаз

В фазовращателе 4 косинусоидальное колебание u₀(t) генератора 2 преобразуется в синусоидальное, а в аттенюаторе 5 его амплитуда становится в два раза меньше, чем на выходе генератора 2. После прохождения этого колебания через управляемые фазовращатели 3.(L+1)-3.N на выходе управляемого фазовращателя 3.N устанавливается суммарный набег фаз

Сформированное с таким сдвигом фазы гармоническое колебание с выхода управляемого фазовращателя 3.N поступает на второй вход балансного фазового детектора 6 в качестве опорного сигнала. При этом на первый вход фазового детектора 6 в качестве сигнального напряжения подается гармоническое колебание с выхода управляемого фазовращателя 3.L. В результате детектирования этого колебания в фазовом детекторе 6 на выходе 7 устройства образуется напряжение, прямо пропорциональное

которое на интервале - М/4<А<М/4 является близким к линейной зависимости: .

Пример. Пусть ; N=5; m₁=11; m₂=7; m₃=5, m₄=3; m₅=2; A=199.

Вычисляем исходные данные: ; L=2; α₁=Amodm₁=1; α₂=3; α₃=4; α₄=1; α₅=1 (A=(1, 3, 4, 1, 1)); μ₁=1; μ₂=1; μ₃=3; μ₄=2; μ₅=1.

В соответствии с полученными в данном примере значениями разрядов α₁, α₂, α₃, α₄ и α₅ в управляемых фазовращателях 3.1-3.5 устанавливаются следующие сдвиги фазы: ; ; ; и .

После прохождения гармонического колебания с выхода генератора 2 через соответствующие фазовращатели на выходе управляемого фазовращателя 3.2 установится набег фазы, равный

а на выходе управляемого фазовращателя 3.5 установится набег фазы, равный

С учетом полученных значений Ф₁ и Ф₂ разность фаз будет равна следующей величине:

В результате детектирования косинусоидального гармонического колебания с фазовым набегом Ф₁ в балансном фазовом детекторе, в котором в качестве опорного сигнала применяется синусоидальное колебание с в два раза меньшей амплитудой и фазовым набегом Ф₂, в соответствии с выражением (12) и приведенными выше исходными данными, получаем выходное напряжение устройства:

Данный результат с точностью в 1,5% совпадает с величиной числа A=199.

Для сравнения, в прототипе [5] для этих же исходных данных получается следующий результат: u_PR(А)=189,424, что на 4,8% отличается от A=199.

Поскольку, как и в прототипе, в заявляемом способе процедура преобразования кода СОК в напряжение базируется на операциях сдвига фазы и определении суммарного набега фазы, то быстродействие преобразования в данном случае будет не хуже быстродействия прототипа.

Источники информации

1. Чернявский А.Ф. и др. Высокоскоростные методы и системы цифровой обработки информации. - Мн.: Белгосуниверситет, 1996. - 376 с.

2. Гитис Э.И., Пискулов Е.А. Аналого-цифровые преобразователи. - М.: Энергоиздат, 1981. - 360 с.

3. Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968. - 440 с.

4. Абрамсон И.Т., Авров О.М., Лапкин Л.Я. Кодирование электрических величин в системе остаточных классов. // Автометрия, №2 (62), 1975, с.23-29.

5. Патент РФ №2220501, МПК Н 03 М 7/18, БИ №36, 2003.

6. Радиоприемные устройства: Учеб. пособие для радиотехнич. спец. вузов / Ю.Т.Давыдов, Ю.С.Данилич, А.П.Жуковский и др.; Под ред. А.П.Жуковского. - М.: Высш. шк., 1989. - 342 с.

Способ преобразования кода системы остаточных классов (СОК) в напряжение, включающий вычисление по модулям m_i произведений разрядов α_i кода числа А в СОК на веса ортогональных базисов μ_i этих разрядов - β_i=(α_iμ_i)modm_i, где m_i - основания СОК; i=1, 2, ... N, формирование опорного гармонического колебания u₀(t)=Ucos(ω·t), где U и ω - соответственно амплитуда и частота гармонического колебания; t - время, отличающийся тем, что из опорного колебания u₀(t) формируют гармоническое колебание u₀₁(t) путем L сдвигов фазы на угол

и гармоническое колебание u₀₂(t) путем сдвига фазы на угол π/2 и (N-L) сдвигов фазы на угол

где j=1, 2, ... L;

L - целая часть результата деления числа N на 2;

k=(L+1), (L+2), ... N,

гармоническое колебание u₀₁(t) подвергают детектированию в балансном фазовом детекторе, а в качестве опорного сигнала фазового детектора используют гармоническое колебание u₀₂(t), амплитуду которого устанавливают в два раза меньше амплитуды гармонического колебания U₀₁(t), причем выходное напряжение балансного фазового детектора при - М/4<А<М/4, где - диапазон разрядной сетки СОК, с погрешностью, не превышающей 10%, прямо пропорционально величине числа А.