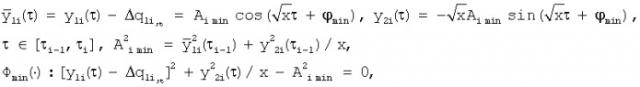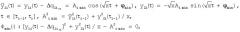Устройство для подавления вибраций упругого элемента переменной жесткости

Устройство для подавления вибраций упругого элемента переменной жесткости

Иллюстрации

Показать все

Реферат

Изобретение относится к демпфированию колебаний упругих элементов конструкции объектов в условиях внешнего нагружения, может быть преимущественно использовано при проектировании и создании перспективных систем управления объектами ограниченной жесткости и является усовершенствованием изобретения по авторскому свидетельству №1596306 [1] (прототип).

Целью изобретения является повышение быстродействия устройства.

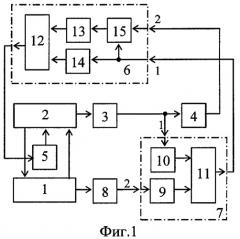
Функциональная схема устройства [1] представлена на фиг 1. Устройство содержит объект 1 управления (подвижное основание), присоединенный к нему упругий элемент 2, датчик 3 отклонения, дифференцирующий блок 4, регулятор 5 жесткости, блок 6 формирования управления жесткостью, блок 7 формирования функции переключения, акселерометр 8.

Блок 6 формирования управления жесткостью состоит из схемы 12 сравнения знаков, двух релейных элементов 13 и 14, сумматора 15.

Блок 7 формирования функции переключения включает два делителя 9 и 10, сумматор 11.

Это устройство реализует закон управления жесткостью упругого элемента в виде:

где q, - фазовые координата и скорость упругого элемента; ω_max, ω_min - максимальная и минимальная частоты колебаний упругого элемента из диапазона возможных изменении; - стационарное положение упругого элемента при максимальной жесткости; ; - ускорение подвижного (вращающегося) основания; J - момент инерции подвижного основания; В - коэффициент взаимовлияния основания и упругого элемента; m - масса упругого элемента; - уравнение линии переключения жесткости; θ - угол логики.

Типовая фазовая траектория упругого элемента, реализующаяся при использовании устройства [1] в условиях действия постоянного нагружения, показана на фиг.2. Здесь где

Характерным является спиралевидность траектории, скручивающейся к стационарному положению (, 0). Этот факт "наследован" от логики [2], построенной для гашения свободных колебаний упругого элемента. При недостаточно широком диапазоне регулирования частоты упругого элемента скручивание спирали - фазовой траектории оказывается медленным, и процесс перевода упругой системы в стационарное состояние (, 0) может существенно затянуться. Вместе с тем, для нагруженного упругого элемента существует возможность его приведения в требуемое стационарное положение по апериодической "попадающей" траектории. При этом время гашения вибраций сокращается.

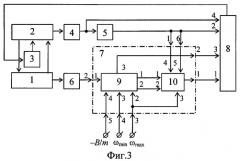
На фиг.3 представлена функциональная схема предлагаемого устройства, на фиг.4 - структурная схема блока расчета внешнего нагружения и стационарных положений, на фиг.5 - то же, блока расчета линии переключения, на фиг.6 - то же, блока формирования управления.

Устройство для подавления вибраций упругого элемента переменной жесткости (фиг.3) содержит: подвижное основание 1, присоединенный к нему упругий элемент 2, регулятор 3 жесткости, датчик 4 отклонений, дифференцирующий блок 5, акселерометр 6, блок 7 формирования функции переключения, блок 8 формирования управления жесткостью.

Блок 7 формирования функции переключения состоит из блока 9 расчета внешнего нагружения и стационарных положений, блока 10 расчета линии переключения.

Блок 9 расчета внешнего нагружения и стационарных положений (фиг.4) содержит: блок 11 умножения, первый и второй делители 12 и 13, первый и второй квадраторы 14 и 15, сумматор 16.

Блок 10 расчета линии переключения (фиг.5) содержит: первый и второй сумматоры 17 и 18, блок умножения 19, делитель 20, первый и второй квадраторы 21 и 22.

Блок 8 формирователя управления жесткостью (фиг.6) содержит: источник 23 постоянного напряжения, первый-четвертый релейные элементы 24-27, первую-третью схемы сравнения знаков 28-30, элемент И 31, элемент ИЛИ 32.

В основу изобретения положено следующее.

Динамика слабодемфированного упругого элемента на подвижном основании может быть представлена в виде [3, 4]

где - фактор внешнего нагружения упругого элемента, связанный с силами инерции, обусловленными движением основания; - ускорение основания; В - коэффициент взаимовлияния основания и упругого элемента; q₁, q₂ - обобщенные координата и скорость колебаний упругого элемента соответственно, m, ω - масса и собственная частота колебаний упругого элемента; - управляющий параметр; ω_max, ω_min - максимальное и минимальное значения собственной частоты колебаний упругого элемента из диапазона возможных изменений.

Заметим, что динамика нагруженного упругого элемента переменной жесткости (1) качественно в значительной мере отличается от динамики свободного осциллятора, задача оптимального по быстродействию гашения колебаний которого поставлена и решена в работах [5-8]. Отличие это проявляется, прежде всего, в том, что стационарная точка (положение устойчивого равновесия) нагруженного упругого элемента не совпадает с началом координат его фазовой плоскости, а определяется действующим нагруженном f(t). Иными словами, недеформированное состояние нагруженного упругого элемента является неустойчивым.

В силу независимости нагружения f(t) от управления V невозможно только лишь целенаправленным изменением жесткости устранить вынужденное движение упругого элемента, но можно и, с технической точки зрения необходимо, управлять его вибрациями относительно траектории вынужденного движения. В этой связи представляется целесообразным осуществлять перевод упругого элемента в стационарное состояние, отвечающее конечному моменту Т интервала управления. Вместе с тем, в общем случае любое изменение внешнего нагружения при t>Т неизбежно приводит к смещению стационарной точки на фазовой плоскости и возникновению колебаний вокруг нее, что само по себе диктует необходимость решения новой задачи управления. Таким образом, всякая вариация внешнего нагружения при отсутствии колебаний продуцирует задачу подавления вибраций упругого элемента. С другой стороны, принадлежность функций f(t) внешнего нагружения к весьма широкому классу, как правило, не позволяет на начальном этапе управления точно аппроксимировать значение f(T) на достаточно продолжительный интервал, что препятствует получению полезного на практике решения в аналитическом виде.

В то же время при высокой эффективности подавления вибраций длительность T интервала управления, вообще говоря, сокращается. В пределе она может стать весьма малой, и тогда задача гашения колебаний может быть сведена к задаче наискорейшего приведения упругого элемента в его текущее стационарное состояние, отвечающее действующему в настоящий момент нагружению. Такой подход является продуктивным, особенно в случаях, когда нет никакой априорной информации о характере нагружения f(t).

Аналогично [5, 8], с использованием формализма принципа максимума получим структуру оптимального управления жесткостью нагруженного упругого элемента (1) в виде:

где

и

- уравнения линий переключения управления на фазовой плоскости упругого элемента (1), причем линия (4) в явном виде не задана.

Отметим, что на самих линиях переключения (3) и (4) управление (2) может быть доопределено из условий его непрерывности справа (слева). При этом оптимальное управление становится кусочно-постоянной функцией и на каждом интервале постоянства может принимать значения либо V=V_max, либо V=V_min

Задача синтеза управления, собственно, и состоит в построении линии (4), применение которой в логике (2) обеспечивает эффективное решение задачи гашения колебаний упругого элемента относительно траектории вынужденного движения.

Трудности, связанные со сложным характером внешнего нагружения, можно обойти за счет использования дельта-метода [9, С.279], согласно которому реальная функция f(t) на последовательности интервалов времени Δ_i=[t_i-1, t_i), аппроксимируется постоянными значениями, например, с_i=f(t_i-1). В общем случае близость кусочно-постоянной аппроксимации к функции f(t) тем лучше, чем короче интервал Δ_i.

При таком подходе на каждом интервале времени t∈Δ_i=[t_i-1, t_i) система уравнений (1) аппроксимируется системой вида:

с начальными условиями

В силу кусочно-постоянного характера управления V стационарным состоянием системы (5) на интервале Δ_i является точка с координатами . Существенно, что стационарные точки нагруженной упругой системы (5) при максимальной и минимальной жесткостях не совпадают. Следствием этого, как будет видно в дальнейшем, является возможность осуществления апериодических режимов приведения упругого элемента в стационарные состояния за счет переключения его жесткости.

Энергия деформаций, запасенная в упругом элементе (5) на интервале Δ_i, под воздействием нагружения с_i составит

и будет минимальна при максимальной жесткости упругой системы. Поэтому с технической точки зрения целесообразно осуществлять перевод упругого элемента (5) в стационарное состояние

а режим максимальной жесткости принять в качестве номинального.

В номинальном режиме полная энергия колебаний упругого элемента (5) относительно стационарного состояния (7) на интервале Δ_i, определяется из соотношения

В соответствии с развиваемым подходом сформулируем задачу параметрически активного подавления вибраций следующим образом.

Требуется на интервале Δ_i согласно структуре оптимального управления (2) выбрать такое значение параметра V=V₀∈{V_min, V_max}, при котором обеспечивается перевод объекта (5) из начального состояния (6) в конечное удовлетворяющее условию

Заметим, что в общем случае динамичного изменения внешнего нагружения q_1i(t_i)≠q₁, _i+1(t_i)=q₁(t_i), q_2i(t_i)≠q₂, _i+1(t_i)=q₂(t_i), E_i(t_i)≠E_i+1(t_i)=E(t_i), поэтому в конце (начале) каждого интервала аппроксимации возможны скачки параметров, обусловленные отклонением математической модели (5) процесса от реальной динамики упругого элемента (1). С учетом (8) в координатном базисе

соотношение (9) эквивалентно требованию минимизации расстояния до точки {0,0}.

Если в координатном базисе (10) дополнительно ввести масштабирование времени, полагая

то с использованием (10), (11) уравнения (5) преобразуются к виду:

при V=V_max

при V=V_min

где x=V_min/V_max∈(0,1) - параметр глубины управления;

Соответственно начальные условия (6) трансформируются следующим образом:

Анализ фазовых траекторий упругой системы. Уравнения (12) описывают свободные колебания одиночного осциллятора с единичной угловой скоростью относительно начала координат и имеют решения

где A_imax, ϕ_max - постоянные начальные амплитуда и фаза колебания соответственно. Последнее соотношение является уравнением фазовой траектории упругого элемента в координатах (10) при максимальной жесткости и определяет дугу окружности с центром в начале координат и радиусом А_imax.

Уравнения (13) путем замены переменной приводятся к системе уравнений

которая, аналогично (12), в координатном базисе (10) описывает свободные колебания одиночного осциллятора, однако, с угловой скоростью относительно центра с координатами

и имеет решение

где A_imin, ϕ_min - постоянные начальные амплитуда и фаза колебания соответственно. Из последнего соотношения следует, что фазовая траектория упругого элемента при минимальной жесткости в координатах (10) есть соответствующая дуга эллипса, полученного путем сжатия окружности с центром в точке (16) и радиусом A_imin относительно оси ординат с коэффициентом .

Движение по всем траекториям относительно их центров осуществляется по часовой стрелке.

На фиг.7 показаны траектории упругого элемента на интервале Δ_i, при максимальной (дуга АВ) и минимальной (дуга АС) жесткостях при тождественных начальных условиях. Без ограничения общности здесь принято, что с_i>0.

Вектор фазовой скорости - касательный к фазовой траектории в начальный момент времени τ_i-1. Согласно (12) и (13) при максимальной жесткости

а при минимальной жесткости

Синтез управления жесткостью. Поскольку критерием выбора значения управляющего параметра V на интервале управления [τ_i-1, τ_i) является минимизация расстояния до начала координат в момент времени τ_i, и при достаточно малой длительности Δτ=τ_i-τ_i-1 интервала управления приращение вектора координат , то основу синтеза управления может составить сравнительный анализ соответствующих компонент векторов и в каждой точке фазовой плоскости (у₁,у₂).

Согласно соотношениям (17) и (18), первые компоненты векторов и тождественны, поэтому достаточно сравнивать лишь их вторые компоненты.

Так, например, в ситуации, представленной на фиг.7,

Следовательно, движение из точки А с максимальной жесткостью приводит к уменьшению компоненты y₂ (дуга АВ) а движение с минимальной жесткостью - напротив, к ее увеличению (дуга АС). Поэтому движение с максимальной жесткостью в данном случае предпочтительней. Ясно, что полученный результат справедлив для любой точки фазовой плоскости, лежащей в области ограниченной прямыми, на которых компоненты векторов и обращаются в нуль (см. (17), (18)).

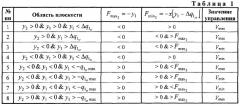
Аналогичным образом проводится анализ компонент и в других областях фазовой плоскости, обобщенные результаты которого приведены в табл.1. При этом в рассмотрение введена еще одна граница - прямая , - которая определена из условия . Учтен также знак внешнего нагружения: с_i>0.

Заметим, что на границах рассмотренных областей фазовой плоскости значение управления V может быть выбрано из условия его непрерывности справа (слева).

На фиг.8 изображена фазовая траектория ABCDEFGG₁ упругого элемента при условии, что С_i=С=const>0, в случае реализации логики управления жесткостью, согласно табл.1. В компактном виде эта логика с точностью до множества нулевой меры (значений управления на линиях переключения) может быть представлена, например, следующим образом:

Из фиг.8 можно сделать вывод о том, что фазовая траектория ABCDFGG₁ упругого элемента "скручивается" к началу координат. Однако с учетом инерционности исполнительного органа последующее переключение управления в точке Н₂ согласно логике (19) на минимальную жесткость обеспечивает движение упругого элемента по эллиптической траектории в точку К₂, где осуществляется переход на максимальную жесткость и начинается движение по дуге окружности K₂L₂, затем снова движение по дуге эллипса L₂М₂, дуге окружности M₂N₂ и т.д. Таким образом, движение упругого элемента после точки G₁ переходит в скользящий режим с частыми переключениями управления в окрестности оси O₁y₁, что нежелательно по следующим причинам:

1) существенно снижается эффект от управления;

2) значительно возрастает нагрузка на исполнительные органы системы управления жесткостью;

3) возможно возбуждение высокочастотных колебаний распределенного упругого элемента.

Однако можно избежать скользящего режима, если "подправить" логику (19) за счет использования "попадающей" траектории (дуга D₁O₁, фиг.8), приходящей точно в начало координат и имеющей аналитическое выражение (при с_i>0):

где . Яркой иллюстрацией здесь служит, например, траектория A₁B₁C₁D₁O₁ (фиг.8).

Применительно к ранее рассматриваемой траектории после точки G₁ движение должно продолжаться с максимальной жесткостью по дуге окружности G₁H₁ до пересечения с линией (20). Переключение в точке Hi на минимальную жесткость обеспечит апериодическое приведение упругого элемента по дуге H₁O₁ в начало координат. Существенно, что согласно построенной логике управления жесткостью, в точке O₁ обеспечивается техническая устойчивость положения упругого элемента (см. фиг.8).

Таким образом, объединяя логику (19) и соотношение (20), представим синтезированную логику управления для случая с_i>0 в виде:

Вариант, когда С_i=С=const<0 может быть получен из логики (21) путем ее центрального симметричного отображения относительно начала координат.

В аналитической форме эта логика может быть представлена следующим образом:

Объединяя (21) и (22) с учетом (7), (10), (13) и (20), получим общий вид логики управления в координатном базисе (q₁, q₂):

где .

Отметим, что при f=0 логика (23) тождественна логике (1) при .

Предлагаемое устройство функционирует следующим образом. После воздействия внешнего нагружения, обусловленного движением основания 1, упругий элемент 2 начинает колебаться с максимальной частотой, поскольку в состоянии покоя жесткость упругого элемента 2 максимальна (из условия снижения амплитуды колебаний, возникающих от действия внешнего нагружения). Датчик 4 отклонения начинает выдавать текущее значение обобщенной координаты q₂ отклонения упругого элемента 2, которое поступает на вход дифференцирующего блока 5, первый вход блока 7 формирования функции переключения и четвертый вход блока 8 формирования управления жесткостью (фиг.3). Текущее значение обобщенной скорости q₂ упругого элемента 2 выдается с выхода дифференцирующего блока 5 на второй вход блока 8 формирования управления жесткостью и на шестой вход блока 7 формирования функции переключения.

Информация об ускорении подвижного основания 1 снимается акселерометром 6 и поступает на второй вход блока 7 формирования функции переключения, а затем - на первый вход блока 9 расчета внешнего нагружения и стационарных положений (фиг.3, 4). В блоке 11 умножения формируется текущее значение внешнего нагружения , которое поступает на первый и второй делители 12 и 13, а также на третий вход блока 8 формирования управления. В первом делителе 12 рассчитывается , во втором делителе 13 - , а в сумматоре 16 вычисляется (фиг.4). Величины и с первого и второго выходов блока 9 расчета внешнего нагружения и стационарных положений поступают на первый и второй входы блока 10 расчета линии переключения (фиг.3, 5), где в первом сумматоре 17 формируется в первом квадраторе поступающее на первый вход второго сумматора 18; в блоке 19 умножения рассчитывается которое поступает на второй вход второго сумматора 18; в делителе 20 формируется пройдя через второй квадратор 22, этот сигнал поступает на третий вход второго сумматора 18. В результате на выходе блока 10 расчета линии переключения согласно (23), формируется сигнал Г, который поступает на первый вход блока 8 формирования управления.

В блоке 8 формирования управления (фиг.6) входные сигналы, пройдя через первый-четвертый релейные элементы 24-27, преобразуются в sgn Г, sgn q₂, sgn f, sgn q₁ соответственно. В первой схеме 28 сравнения знаков осуществляется проверка условия sgn Г=-1, причем постоянный сигнал - 1 поступает на второй вход этой схемы с источника 23 постоянного напряжения. Во второй схеме 29 сравнения знаков проверяется условие sgn q₂=sgn q₁, а в третьей схеме 30 сравнения знаков - условие sgn q₂=-sgn f. Логические элементы И 31 и ИЛИ 32 реализуют логику управления (23), выдавая на выходе блока 8 формирования управления сигнал, равный логической единице, если необходимо установить V=V_max и логическому нулю, если V=V_min.

В остальном функционирование предлагаемого устройства аналогично известному.

Положительный эффект - сокращение длительности переходных процессов в предлагаемом устройстве достигается за счет осуществления перевода упругого элемента в стационарное состояние, отвечающее минимальному коэффициенту динамичности, по "попадающей" траектории.

Таким образом, отличительные признаки предлагаемого устройства способствуют достижению поставленной цели.

Источники информации

1. А.С. СССР №1596306, G 05 В 13/00, 1989 (прототип).

2. А.С. СССР №1129585, G 05 В 11/01, 1983.

3.Шиманский А.Ю. Динамический расчет судовых конструкций. - Л.: Судпромгиз, 1963. - 444 с.

4. Ликинз П. Уравнение в квазикоординатах для космических аппаратов нежесткой конструкции // Ракетная техника и космонавтика. 1975. Т.13, №4. С.137-140.

5. Шалымов С.В. Гашение колебаний упругой системы за счет оптимального управления жесткостью. Часть 1. Постановка задачи, структура управления, инвариант оптимального процесса гашения колебаний // Изв. вузов. Приборостроение. 1998. Т.41, №6. С.36-40.

6. Шалымов С.В. Гашение колебаний упругой системы за счет оптимального управления жесткостью. Часть 2. Уравнения линий переключения управления // Изв. вузов. Приборостроение. 1999. Т.42, №3-4. С.46-50.

7. Шалымов С.В. Гашение колебаний упругой системы за счет оптимального управления жесткостью. Часть 3. Построение оптимальных линий переключения жесткости // Изв. вузов. Приборостроение. 1999. Т.42, №7. С.39-47.

8. Шалымов С.В. Оптимальное гашение колебаний простых упругих систем с управляемой жесткостью - СПб.: МО РФ, 2001. - 101 с.

9. Вибрации в технике. Справочник в шести томах. Т.6. Защита от вибрации и ударов / Под ред. К.В.Фролова. - М.: Машиностроение, 1995. - 456 с.

1. Устройство для подавления вибраций упругого элемента переменной жесткости, содержащее подвижное основание с присоединенным к нему упругим элементом, к выходу упругого элемента подключен датчик отклонений упругого элемента, а ко входу - регулятор жесткости упругого элемента, выход датчика отклонений упругого элемента соединен с входом дифференцирующего блока и первым входом блока формирования функции переключения, выход подвижного основания подключен ко входу акселерометра, выход которого связан со вторым входом блока формирования функции переключения, первый выход которого соединен с первым входом блока формирования управления, выход дифференцирующего блока подключен ко второму входу блока формирования управления, выход которого связан со входом регулятора жесткости упругого элемента, отличающееся тем, что оно дополнительно снабжено первым, вторым и третьим источниками постоянного напряжения, выходы которых подключены соответственно к третьему, четвертому и пятому входам блока формирования функции переключения, шестой вход которого соединен с выходом дифференцирующего блока, а второй выход - с третьим входом блока формирования управления, четвертый вход блока формирования управления связан с выходом датчика отклонений упругого элемента.

2. Устройство по п.1, отличающееся тем, что блок формирования функции переключения содержит блок расчета внешнего нагружения и стационарных положений и блок расчета линии переключения, причем второй, третий, четвертый и пятый входы блока формирования функции переключения соединены соответственно с первым, вторым, третьим и четвертым входами блока расчета внешнего нагружения и стационарных положений, первый, второй и третий выходы которого подключены соответственно к первому, второму входам блока расчета линии переключения и ко второму выходу блока формирования функции переключения, третий, четвертый и пятый входы блока расчета линии переключения связаны соответственно с третьим, первым и шестым входами блока формирования функции переключения, первый выход которого соединен с выходом блока расчета линии переключения.

3. Устройство по п.1, отличающееся тем, что блок формирования управления содержит источник постоянного напряжения, первый - четвертый релейные элементы, первую, вторую и третью схемы сравнения знаков, логический элемент И, логический элемент ИЛИ, причем первый вход блока формирования управления через первый релейный элемент соединен с первым входом первой схемы сравнения знаков, второй вход которой подключен к выходу источника постоянного напряжения, а выход - к первому входу элемента И, второй вход блока формирования управления через второй релейный элемент соединен с первыми входами второй и третьей схем сравнения знаков, третий вход блока формирования управления через третий релейный элемент подключен ко второму инверсному входу третьей схемы сравнения знаков, выход которой соединен со вторым входом элемента И, четвертый вход блока формирования управления через четвертый релейный элемент связан со вторым входом второй схемы сравнения знаков, выход которой соединен с первым входом элемента ИЛИ, второй вход элемента ИЛИ подключен к выходу элемента И, а выход - к выходу блока формирования управления.

4. Устройство по п.2, отличающееся тем, что блок расчета внешнего нагружения и стационарных положений содержит блок умножения, первый и второй квадраторы, первый и второй делители, сумматор, причем первый вход блока расчета внешнего нагружения и стационарных положений через последовательно соединенные блок умножения, первый делитель и сумматор подключен ко второму выходу блока расчета внешнего нагружения и стационарных положений, выход блока умножения связан с третьим выходом, а через второй делитель - с первым выходом блока расчета внешнего нагружения и стационарных положений, второй и третий входы блока расчета внешнего нагружения и стационарных положений через первый и второй квадраторы соединены со вторыми входами второго и первого делителей соответственно, четвертый вход блока расчета внешнего нагружения и стационарных положений подключен ко второму входу блока умножения, выход второго делителя связан со вторым входом сумматора.

5. Устройство по п.2, отличающееся тем, что блок расчета линии переключения содержит первый и второй сумматоры, блок умножения, делитель, первый и второй квадраторы, причем первый вход блока расчета линии переключения через последовательно соединенные первый сумматор, первый квадратор и второй сумматор связан с выходом блока расчета линии переключения, второй вход блока расчета линии переключения через блок умножения подключен ко второму входу второго сумматора, третий вход блока расчета линии переключения через последовательно соединенные делитель, второй квадратор связан с третьим входом второго сумматора, четвертый и пятый входы блока расчета линии переключения подключены ко вторым входам первого сумматора и делителя соответственно, второй вход блока умножения соединен с выходом первого сумматора.