Способ подтверждения подлинности дискретного сообщения

Способ подтверждения подлинности дискретного сообщения

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области способов и устройств криптографического преобразования данных.

В совокупности признаков заявляемого способа используются следующие термины:

ключ (или ключ защиты) представляет собой комбинацию битов, известную только законному пользователю;

шифрование есть процесс криптографического преобразования блоков данных с использованием ключа, переводящий данные в криптограмму, представляющую собой псевдослучайную последовательность знаков, из которой получение информации без знания ключа практически невыполнимо;

дешифрование есть процесс, обратный процедуре шифрования; дешифрование обеспечивает восстановление информации по криптограмме при знании ключа;

двоичный вектор числа - это сигнал в виде последовательности нулевых и единичных битов, соответствующей представлению числа в двоичной системе исчисления.

Известны способы подтверждения подлинности дискретного сообщения с использованием функций подтверждения подлинности, с использованием механизмов симметричного шифрования, с использованием шифрования с открытым ключом (см., например, [1] стр.136-147).

В известных способах подтверждение подлинности дискретного сообщения реализуется путем включения дополнительной избыточной информации. Эта информация является частью формата сообщения.

Однако известные способы-аналоги подтверждения подлинности дискретного сообщения требуют поддержания специальным сервером ключей.

Наиболее близким по своей технической сущности к заявляемому способу подтверждения подлинности дискретного сообщения является способ с использованием механизмов симметричного шифрования, описанный в [1] на стр.139-147.

Способ-прототип включает в себя формирование на передающей стороне ключа К между пользователями сети длиною n бит, шифрование с использованием ключа К дискретного сообщения, формирование двоичного вектора D, соответствующего дате и времени передачи дискретного сообщения, формирование двоичного вектора секретного параметра β, формирование двоичного вектора идентификации I длиною k бит путем шифрования двоичного вектора секретного параметра β с использованием ключа К, добавление к дискретному сообщению двоичного вектора D, соответствующему дате и времени передачи дискретного сообщения, и двоичного вектора идентификации I, а на приемной стороне осуществляют формирование двоичного вектора ключа К между пользователями сети, определяют двоичный вектор секретного параметра β путем дешифрования двоичного вектора идентификации I и при его совпадении с установленным секретным параметром осуществляют дешифрование дискретного сообщения с использованием ключа К.

Однако способ-прототип имеет недостаток. Поскольку для шифрования и дешифрования ключ К между пользователями сети используется многократно при передаче различный дискретных сообщений, то это позволяет злоумышленнику реализовать задержку дискретных сообщений, их удаление, подмену или повтор (см. [1], стр.144). При этом не обеспечивается защита от таких действий, поскольку само дискретное сообщение не изменяется. Для того, чтобы быть уверенным, что принимаемое дискретное сообщение не является копией ранее полученного, используют механизм перезапроса, что снижает быстродействие процесса подтверждения подлинности дискретного сообщения (см. [1], стр.144), или используют механизм нумерации сообщений. Однако в этом случае в вычислительной сети с большим числом пользователей отдельный пользователь не в состоянии отслеживать информацию о всех взаимодействиях в сети (см. [1], стр.143)

Изобретение направлено на обеспечение отбраковки ложных сообщений и повышение быстродействия процесса подтверждения подлинности дискретного сообщения.

Это достигается тем, что в известном способе подтверждения подлинности дискретного сообщения, заключающемся в том, что на передающей стороне формируют ключ К между пользователями сети длиною n бит, осуществляют шифрование дискретного сообщения, формируют двоичный вектор D, соответствующий дате и времени передачи дискретного сообщения, формируют двоичный вектор секретного параметра β, формируют двоичный вектор идентификации I длиною k бит путем преобразования двоичного вектора секретного параметра β, добавляют к дискретному сообщению двоичный вектор D, соответствующий дате и времени передачи дискретного сообщения, и двоичный вектор идентификации I, а на приемной стороне осуществляют формирование двоичного вектора ключа К между пользователями сети, выделяют двоичный вектор секретного параметра β и осуществляют дешифрование дискретного сообщения, согласно изобретению на передающей стороне пользователи сети дополнительно формируют случайный двоичный вектор ξ длиною n бит, дополнительно формируют двоичный вектор ключа защиты α путем сложения по модулю два битов случайного двоичного вектора ξ с битами двоичного вектора ключа К и передают его вместе с дискретным сообщением, формируют двоичный вектор секретного параметра β путем сжатия случайного двоичного вектора ξ до n/2 бит и используют его для шифрования дискретного сообщения, формируют двоичный вектор идентификации I путем преобразования в кольце класса вычетов по модулю p двоичного вектора D, соответствующего дате и времени передачи дискретного сообщения, и двоичного вектора секретного параметра β D·β≡I(mod p), где p=2^k, а на приемной стороне осуществляют выделение случайного двоичного вектора ξ путем сложения по модулю два битов двоичного вектора ключа К с битами двоичного вектора ключа защиты α, формируют двоичный вектор секретного параметра β путем сжатия случайного двоичного вектора ξ до n/2 бит, формируют двоичный вектор идентификации I путем преобразования в кольце класса вычетов по модулю p двоичного вектора D, соответствующего дате и времени передачи дискретного сообщения, и двоичного вектора секретного параметра β D·β≡I(mod p), где p=2^k, сравнивают полученный двоичный вектор идентификации I с переданным и при их совпадении осуществляют дешифрование дискретного сообщения с использованием двоичного вектора секретного параметра β.

Перечисленная совокупность существенных признаков исключает возможность определения секретного параметра β, а также ключей К между пользователями сети, так как для их определения требуется знание случайного двоичного вектора ξ, который изменяется для каждого передаваемого дискретного сообщения случайным образом. Это не позволяет злоумышленнику сформировать двоичный вектор идентификации I, соответствующий заданному времени передачи дискретного сообщения, и реализовать задержку дискретных сообщений, их удаление, подмену или повтор. При этом исключается применение механизма перезапроса для повторной передачи дискретного сообщения, что повышает быстродействие процесса подтверждения подлинности дискретного сообщения.

Возможность технической реализации заявленного способа поясняется следующим образом.

Случайный двоичный вектор ξ длиною n бит сформируют, например, путем использования генератора случайных чисел в комбинации с показаниями таймера (см. [1], стр.66).

Двоичный вектор секретного параметра β формируют путем сжатия случайного двоичного вектора ξ до n/2 бит. Для этого случайный двоичный вектор ξ разбивают на два блока одинаковой длины n/2 бит и формируют из двух блоков двоичный вектор путем сложения их битов по модулю два (см. [1], стр.101).

Ключ К пользователи сети определяют путем вычислений, использующих свой секретный ключ и открытый ключ пользователя, вступающего в связь, и выполняемых в соответствии с протоколом 7, представленным в [1] на стр.71, или алгоритмом, представленным в [2] на стр.61 и [4] на стр.139.

Двоичный вектор идентификации I формируют путем перемножения числа, соответствующего двоичному вектору, дате и времени передачи дискретного сообщения D, на число, соответствующее двоичному вектору секретного параметра β, и приведения полученного результата по модулю p=2^k, то есть определения остатка от деления полученного результата на число p=2^k. При этом знание чисел I и D не позволяет определить число β за приемлемое время, так как из-за отсутствия обратных элементов по отношению к числу D для четных чисел в кольце класса вычетов по модулю p=2^k задача нахождения числа β может быть решена методом тотального перебора и сводится к нахождению целого числа x, удовлетворяющего уравнению x·p+I=β·D. Поскольку числа p и I имеют порядок 2^k а число β имеет порядок 2^n/2, то порядок числа x будет иметь значение не менее 2^n/2-k. Так как длину двоичного вектора идентификации I выбирают равной 16-32 бит (см.[1], стр.137) k=16-32, то, в соответствии с Российским стандартом ГОСТ 28147-89 [4], для ключа длиною 256 бит n/2=128 потребуется 2⁹⁶=10²⁸ вычислений для определения числа x. Если вскрытие ключа будет осуществляться с помощью ЭВМ, имеющей тактовую частоту 1 ГГц (10⁹ операций в сек), то число операций, выполняемое этой ЭВМ в течение года, будет составлять 3·10¹⁵, а время вскрытия числа β не превысит 3·10¹² лет. В соответствии с стандартами США DES и AES, использующих ключи длиною 128 бит, время вскрытия числа β составит не менее 1 месяца. При этом вскрытие числа β не позволяет вскрывать случайный двоичный вектор ξ и ключ К.

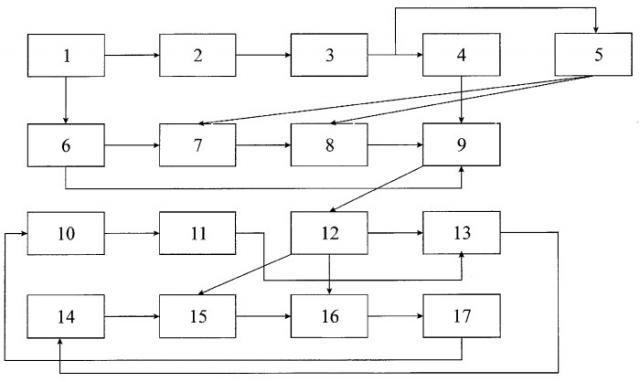
Предлагаемый способ может быть реализован с помощью ЭВМ или вычислительного устройства, представленного блок-схемой на чертеже, где

блок 1 - устройство ввода-вывода;

блок 2 - устройство формирования ключа;

блок 3 - устройство формирования случайного двоичного вектора;

блок 4 - устройство формирования ключа защиты;

блок 5 - устройство формирования секретного параметра;

блок 6 - устройство формирования даты и времени передачи дискретного сообщения;

блок 7 - устройство формирования идентификатора дискретного сообщения;

блок 8 - шифрующее устройство;

блок 9 - передающее устройство;

блок 10 - устройство ввода-вывода;

блок 11 - устройство формирования ключа;

блок 12 - приемное устройство;

блок 13 - устройство выделения случайного двоичного вектора;

блок 14 - устройство формирования секретного параметра;

блок 15 - устройство формирования идентификатора дискретного сообщения;

блок 16 - сравнивающее устройство;

блок 17 - дешифрующее устройство.

Для простоты описания работы устройства будем пользоваться малыми числами. Будем считать, что пользователи сети используют ключи длиною 32 бита (n=32), а для идентификатора дискретного сообщения используют 8 бит (k=8).

С помощью блока 1 осуществляют ввод дискретного сообщения, своего секретного ключа и открытого ключа пользователя, которому передается дискретное сообщение.

В блоке 2 формируют ключ между пользователями сети в виде двоичного вектора длиною n=32 бита, используя при этом свой секретный ключ и открытый ключ пользователя, которому передается дискретное сообщение.

К={11100000100001100010100111101000}.

В блоке 3 формируют случайный двоичный вектор

ξ={11100100101101110110011010101111}.

В блоке 4 формируют двоичный вектор ключа защиты путем сложения по модулю два битов ключа К с битами случайного двоичного вектора ξ

α={00000100001100010100111101000111}.

В блоке 5 формируют двоичный вектор секретного параметра β путем разбиения случайного двоичного вектора ξ на два блока

ξ={11100100101101110110011010101111}.

и формирования двоичного вектора длиною 16 бит путем сложения по модулю два битов двоичного вектора первого блока с битами двоичного вектора второго блока

β={1000001000011000}.

Этому двоичному вектору соответствует число β=2¹⁵+2⁹+2⁴+2³=33304 в десятичной системе исчисления.

В блоке 6 формируют двоичный вектор, соответствующий дате и времени передачи дискретного сообщения. Для этого 4 бита выделяют для передачи месяца, следующие 5 бит используют для передачи дня месяца, следующие 4 биты используют для передачи часа, а следующие 6 бит используют для передачи минут. Например, для января (первого) месяца, 7-го числа, 8 часов и 13 минут двоичный вектор D будет иметь вид

D={0001001111000001101}.

Этому двоичному вектору соответствует число D=2¹⁵+2¹²+2¹¹+2¹⁰+2⁹+2³+2²+1=40461 в десятичной системе исчисления.

В блоке 7 формируют двоичный вектор идентификации дискретного сообщения I путем умножения числа D на число β и приведения полученного результата по модулю p=2^k=256

40461·33304=133683144=200 mod(256).

Этому числу соответствует двоичный вектор

I={11001000}.

В блоке 8 осуществляют шифрование дискретного сообщения, а в блоке 9 присоединяют к зашифрованному дискретному сообщению двоичный вектор, соответствующий дате и времени передачи дискретного сообщения D, двоичный вектор ключа защиты α, двоичный вектор идентификации дискретного сообщения I и передают их по линии связи.

С помощью блока 10 осуществляют ввод дискретного сообщения, своего секретного ключа и открытого ключа отправителя дискретного сообщения.

В блоке 11 формируют ключ между пользователями сети в виде двоичного вектора длиною n=32 бита, используя при этом свой секретный ключ и открытый ключ отправителя дискретного сообщения.

К={11100000100001100010100111101000}.

В блоке 12 осуществляют прием переданных данных.

В блоке 13 выделяют случайный двоичный вектор ξ. Для этого складывают по модулю два биты сформированного на приемной стороне двоичного вектора ключа К с битами принятого двоичного вектора ключа защиты α

α={00000100001100010100111101000111}.

ξ={11100100101101110110011010101111}.

В блоке 14 формируют двоичный вектор секретного параметра β. Для этого разбивают случайный двоичный вектор ξ на два блока

ξ={11100100101101110110011010101111}.

и формируют двоичный вектор длиною 16 бит путем сложения по модулю два битов двоичного вектора первого блока с битами двоичного вектора второго блока

β={1000001000011000}.

Этому двоичному вектору соответствует число β=2¹⁵+2⁹+2⁴+2³=33304 в десятичной системе исчисления.

В блоке 15 формируют двоичный вектор идентификации дискретного сообщения I путем умножения принятого числа D на сформированное на приемной стороне число β и приведения полученного результата по модулю p=256

40461·33304=133683144200 mod(256).

Этому числу соответствует двоичный вектор

I={11001000}.

В блоке 16 сравнивают сформированный на приемной стороне двоичный вектор идентификации дискретного сообщения I с переданным и при их совпадении осуществляют декодирование дискретного сообщения. При этом двоичный вектор идентификации дискретного сообщения I изменяется случайным образом для каждого передаваемого дискретного сообщения и для каждого двоичного вектора, соответствующего дате и времени передачи дискретного сообщения. При приеме дискретного сообщения от того же пользователя сети с двоичным вектором, соответствующим дате и времени передачи предыдущего дискретного сообщения, и двоичным вектором идентификации предыдущего дискретного сообщения его классифицируют как ложное дискретное сообщение и его отбраковывают.

Реализация предлагаемого способа не вызывает затруднений, так как все блоки и узлы, входящие в устройство, реализующее способ, общеизвестны и широко описаны в технической литературе.

Источники информации

1. С.Мафтик. Механизмы защиты в сетях ЭВМ, М., 1993 г.

2. В.И.Нечаев. Элементы криптографии. Основы теории защиты информации, М., Высшая школа, 1999 г.

3. В.И.Тупота. Адаптивные средства защиты информации в вычислительных сетях. - М.: Радио и связь, 2002, - 176 с.

4. Российский стандарт шифрования стандарт СССР ГОСТ 28147-89 системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования.

Способ подтверждения подлинности дискретного сообщения, заключающийся в том, что формируют ключ К между пользователями сети длиною n бит, осуществляют шифрование дискретного сообщения, формируют двоичный вектор D, соответствующий дате и времени передачи дискретного сообщения, формируют двоичный вектор секретного параметра β, формируют двоичный вектор идентификации I длиною k бит путем преобразования двоичного вектора секретного параметра β, добавляют к дискретному сообщению двоичный вектор D, соответствующий дате и времени передачи дискретного сообщения, и двоичный вектор идентификации I, а на приемной стороне осуществляют формирование двоичного вектора ключа К между пользователями сети, определяют двоичный вектор секретного параметра β и при его совпадении с установленным секретным параметром осуществляют дешифрование дискретного сообщения, отличающийся тем, что, пользователи сети на передающей стороне формируют случайный двоичный вектор ξ длиною n бит, формируют двоичный вектор ключа защиты α путем сложения по модулю два битов случайного двоичного вектора ξ с битами двоичного вектора ключа К и передают его вместе с дискретным сообщением, формируют двоичный вектор секретного параметра Р путем сжатия случайного двоичного вектора ξ до n/2 бит и используют его для шифрования дискретного сообщения, формируют двоичный вектор идентификации I путем преобразования в кольце класса вычетов по модулю p двоичного вектора D, соответствующего дате и времени передачи дискретного сообщения, и двоичного вектора секретного параметра β D·β≡I(mod p), где p=2^k, а на приемной стороне осуществляют выделение случайного двоичного вектора ξ путем сложения по модулю два битов двоичного вектора ключа К с битами двоичного вектора ключа защиты α, формируют двоичный вектор секретного параметра β путем сжатия случайного двоичного вектора ξ до n/2 бит, формируют двоичный вектор идентификации I путем преобразования в кольце класса вычетов по модулю p двоичного вектора D, соответствующего дате и времени передачи дискретного сообщения, и двоичного вектора секретного параметра β D·β≡I(mod p), где р=2^k, сравнивают полученный двоичный вектор идентификации I с переданным и при их совпадении осуществляют дешифрование дискретного сообщения с использованием двоичного вектора секретного параметра β.