Способ определения геодезических координат объекта

Способ определения геодезических координат объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к геодезии, в частности к способам определения геодезических координат объекта. Объектами могут служить участки земной поверхности, строения, воздушные и космические летательные аппараты (ЛА), морские и речные суда и т.п. Изобретение может быть использовано в системах воздушной, морской и космической навигации, для целеуказания, а также при наземной послеполетной обработке зарегистрированных данных средств бортовых измерений летательного аппарата для анализа погрешностей определения геодезических координат объекта с известными геодезическими координатами бортовыми средствами, в частности радиолокатором, лазерным дальномером.

Для определения геодезических координат объекта на носителе (в качестве которого может быть использован летательный аппарат, корабль, наземная стационарная или подвижная установка) размещают навигационный комплекс и устройство измерения относительного положения объекта (т.е. положения объекта относительно этого устройства). При этом геодезические координаты навигационного комплекса (долгота L_A, широта B_A и высота Н_A) либо определены заранее путем выполнения его геодезической привязки (наземные стационарные радиосистемы ближней или дальней навигации), либо измеряются на борту подвижного носителя с помощью, например, глобальной навигационной спутниковой системы (ГНСС) [ГОСТ Р 51794-2001. Государственный стандарт Российской Федерации. Аппаратура радионавигационная глобальной навигационной спутниковой системы и глобальной системы позиционирования. Системы координат. Методы преобразований координат определяемых точек. - М.: Госстандарт России, с.1...2]. В дальнейшем рассмотрим, как общий, случай размещения навигационного комплекса и устройства измерения положения объекта на борту подвижного носителя.

Определение геодезических координат: широты В, долготы L и высоты Н объекта по измеренным геодезическим координатам: широте B_A, долготе L_A и высоте H_A навигационного комплекса и измеренному вектору относительной дальности до объекта, называется прямой пространственной геодезической задачей и представлено, например, в [Морозов В.П. Курс сфероидической геодезии. - М.: Недра, 1979, с.196-197].

Определим используемую ниже терминологию. Вектор положения какого-либо объекта в референцной геодезической системе координат (СК), связанной с общеземным эллипсоидом (ОЗЭ), задают геодезическими координатами: широтой В, долготой L и высотой Н [ГОСТ Р 51794-2001, с.1...2]. Размер и форму ОЗЭ задают двумя параметрами: большой полуосью а и эксцентриситетом е [там же, с.1, 3]. Геоцентрической широтой Ф объекта называют угол между экваториальной плоскостью ОЗЭ и прямой, соединяющей центр ОЗЭ с объектом [Морозов В.П. Курс сфероидической геодезии. - М.: Недра, 1979, с.189].

Под угловой ориентацией подвижного носителя навигационного комплекса (например, ЛА) относительно земли понимают значения углов Эйлера, в частности тангажа ϑ, крена γ и рыскания ψ [ГОСТ 20058-80. Государственный стандарт Союза ССР. Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. - М.: Государственный комитет СССР по стандартам, 1981. с.9], либо матрицу направляющих косинусов [там же, с.43] между осями OX, OY, OZ связанной СК и осями OX_g, OY_g, OZ_g, нормальной СК [там же, с.4]. Начало О нормальной СК OX_g Y_g Z_g совпадает с началом связанной СК подвижного носителя, ось OY_g направлена по нормали к поверхности ОЗЭ, ось ОХ_g направлена в сторону оси вращения ОЗЭ. Угол курса ψ_к отличается от угла рыскания ψ противоположным направлением положительного отсчета. Как видим, нормальная СК, принятая в динамике ЛА в атмосфере, совпадает с топоцентрической декартовой прямоугольной СК О₀ξςη, принятой в сфероидической геодезии. Вектор относительной дальности до объекта в топоцентрической СК задают полярными координатами - наклонной относительной дальностью D, геодезическим азимутом A₀ и зенитным расстоянием Z₀ [Морозов В.П. Курс сфероидической геодезии. - М.: Недра, 1979, с.189...190].

Введем локальную декартову геоцентрическую прямоугольную СК O_гX_гY_гZ_г, связанную с положением подвижного носителя навигационного комплекса. Начало О_г ее поместим в центре ОЗЭ. Плоскость О_гХ_гY_г расположим в меридианной плоскости, содержащей начало О нормальной СК ЛА, ось О_гX_г направим вдоль пересечения меридианной плоскости с экваториальной плоскостью ОЗЭ от точки О_г к проекции точки О на это пересечение, ось O_гY_г направим в меридианной плоскости на северный полюс ОЗЭ, ось O_гZ_г дополняет СК до правой и лежит в экваториальной плоскости ОЗЭ.

Прототипом изобретения является способ определения геодезических координат объекта, представленный в [Морозов В.П. Курс сфероидической геодезии. - М.: Недра, 1979, с.196...197], в котором измеряют геодезические координаты: долготу L_A, широту В_A и высоту H_A размещенного на носителе навигационного комплекса и с помощью размещенного на упомянутом носителе устройства определения положения объекта - вектор положения =(D A₀ Z₀) объекта относительно упомянутого устройства, по измеренным данным вычисляют в декартовой геоцентрической системе координат компоненты вектора положения навигационного комплекса и вектора положения объекта относительно упомянутого устройства и определяют в этой системе координат вектор положения объекта суммированием вычисленных упомянутых компонент векторов, по вектору положения объекта определяют геодезические координаты объекта: долготу L, широту В и высоту Н.

Компоненты вектора положения навигационного комплекса в декартовой геоцентрической СК вычисляют по формулам

где N_A - вспомогательная переменная, а компоненты вектора положения объекта относительно устройства вычисляют по формулам

где - компоненты вектора положения объекта в нормальной СК.

В известном способе для определения геодезической долготы L объекта сначала вычисляют приращение l геодезической долготы объекта

по компонентам вектора положения объекта по осям геоцентрической системы координат в экваториальной плоскости общеземного эллипсоида с учетом знаков этих компонентов, а затем саму геодезическую долготу объекта

L=L_A+l.

Геодезическую широту В объекта определяют из уравнения связи тангенса t геодезической широты с компонентами вектора положения объекта

в котором введены вспомогательные переменные и константы:

Как видно из правой части выражения (5), величина t₀ представляет значение тангенса геоцентрической широты объекта.

Для вычисления геодезической широты объекта применяют итерационную процедуру

до достижения заданной точности значения тангенса t геодезической широты В. Из (6) видно, что геодезическую широту объекта определяют многократным уточнением приближенного значения ее тангенса непосредственно из уравнения связи (3). После чего из выражения (4) определяют саму геодезическую широту объекта

Геодезическую высоту Н объекта вычисляют по формуле

Недостатком этого способа определения геодезических координат L, В, Н объекта являются неприемлемые для некоторых целей погрешности δL, δB, δH их определения. Эти погрешности вызваны следующими обстоятельствами.

Во-первых, измеряемые геодезические координаты навигационного комплекса носителя являются координатами его определенной части. Так, при использовании на носителе аппаратуры ГНСС измеряются координаты L_A, B_A и Н_A антенны этой аппаратуры. Вектор положения объекта определяет вектор положения объекта относительно размещенного на упомянутом носителе устройства определения положения объекта. Антенна аппаратуры ГНСС упомянутого навигационного комплекса и упомянутое устройство пространственно разнесены относительно друг друга, причем величина этого разноса может изменяться от нескольких метров на ЛА до десятков и сотен метров на корабле и определяет величину методической погрешности измерения вектора относительного положения объекта в известном способе.

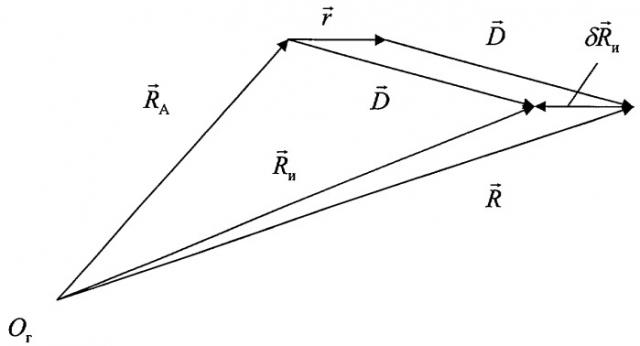
Обозначим в декартовой геоцентрической СК через вектор положения навигационного комплекса, через - вектор положения упомянутого устройства относительно упомянутого навигационного комплекса, через - вектор положения объекта относительно упомянутого устройства, тогда вектор положения объекта определяется следующей суммой (фиг.1):

В известном способе определения геодезических координат объекта вектор его положения определяют согласно выражениям (1) другой суммой

не содержащей вектора положения объекта относительно упомянутого устройства. Это приводит в известном способе к погрешности вычисления геоцентрических декартовых координат объекта, определяемой из выражений (9) и (10)

Максимальные погрешности измерения дальности современными лазерными дальномерами не превышают 1 м. Следовательно, указанные выше значения (от нескольких до десятков и сотен метров) погрешностей вычисления геоцентрических декартовых координат объекта известным способом могут оказаться недопустимо большими. Это приводит к соответствующим погрешностям δL, δВ, δН определения геодезических координат объекта. Поэтому известный способ может приводить к определению геодезических координат объекта с недопустимо большой методической погрешностью.

Во-вторых, снижение погрешности δВ вычисления геодезической широты В объекта при итерационной процедуре (6) проходит медленно и с неизвестным заранее количеством итераций (для достижения заданной точности). В вычислительных системах реального времени неопределенное количество итераций является существенным недостатком.

В-третьих, в известном способе при определении приращения l (2) геодезической долготы объекта отношение неограниченно возрастает по модулю при значении , которое может выполняться при любых значениях геодезической широты В объекта. Поэтому вычисление значений тангенсов как геодезической долготы l (2), так и геодезической широты В (7) объекта приводит к резкому возрастанию погрешностей их расчета при значениях углов, близких к .

Действительно, из выражения (7) следует, что погрешности δB измерения геодезической широты объекта приводят к следующим погрешностям вычисления значения ее тангенса

Правая часть данного выражения неограниченно возрастает при значениях геодезической широты объекта, близких к . Правая часть выражения (2) для расчета приращения l геодезической долготы объекта содержит аналогичную особенность при значении составляющей вектора положения объекта, т.е. при значениях приращения l геодезической долготы объекта, близких к .

В-четвертых, указанное резкое возрастание погрешности расчета тангенса геодезической широты В (4) при значениях углов, близких к , согласно выражению (8) приводит к неопределенному результату расчета геодезической высоты Н объекта, поскольку при этом величина R_h стремится к нулю, множитель - к бесконечности, а их произведение может дать произвольный непредсказуемый результат.

Задачей изобретения является повышение точности определения геодезических координат объекта.

Задача решается с помощью способа определения геодезических координат объекта, в котором измеряют геодезические координаты размещенного на носителе навигационного комплекса и с помощью размещенного на упомянутом носителе устройства определения положения объекта - вектор положения объекта относительно упомянутого устройства, по измеренным данным вычисляют в декартовой геоцентрической системе координат компоненты вектора положения объекта относительно упомянутого устройства и вектора положения навигационного комплекса и определяют в этой системе координат вектор положения объекта суммированием вычисленных упомянутых компонент, по вектору положения объекта определяют геодезические координаты объекта, отличающегося тем, что дополнительно измеряют вектор положения упомянутого устройства относительно упомянутого навигационного комплекса и угловую ориентацию носителя относительно земли, при упомянутом вычислении компонент в декартовой геоцентрической системе координат дополнительно вычисляют компоненты упомянутого вектора положения упомянутого устройства относительно упомянутого навигационного комплекса и дополнительно их учитывают при упомянутом суммировании.

С целью снижения погрешности определения геодезических широты и высоты объекта геодезическую широту объекта определяют уточнением как минимум один раз приближенного значения ее тангенса t путем вычитания корректирующей поправки, равной отношению значения функции

где t₀ - тангенс геоцентрической широты объекта,

е - эксцентриситет общеземного эллипсоида,

a - большая полуось общеземного эллипсоида,

R_h - модуль проекции вектора положения объекта на экваториальную плоскость общеземного эллипсоида, к производной этой функции по t при значении t, равном предшествующему приближенному его значению.

С целью снижения погрешности определения геодезических широт начальное приближенное значение тангенса t геодезической широты определяют по тангенсу t₀ геоцентрической широты объекта по формуле

С целью снижения погрешности определения геодезических широты и высоты объекта геодезическую широту В объекта определяют уточнением как минимум один раз приближенного ее значения путем вычитания корректирующей поправки, равной отношению значения функции

где Ф - геоцентрическая широта объекта,

R - модуль вектора положения объекта,

к производной этой функции по В при значении В, равном предшествующему приближенному ее значению.

С целью снижения погрешности определения геодезических широты и высоты объекта начальное приближенное значение геодезической широты В определяют по геоцентрической широте Ф объекта по формуле

С целью снижения погрешности определения геодезических широты и высоты объекта геоцентрическую широту Ф объекта определяют по величинам отношений проекции вектора положения объекта на ось вращения общеземного эллипсоида и модуля проекции этого вектора на экваториальную плоскость общеземного эллипсоида к модулю этого вектора.

С целью снижения погрешности определения геодезической высоты объекта геодезическую высоту Н объекта определяют по формуле

где - компонент вектора положения объекта в декартовой геоцентрической системе координат, параллельный оси вращения общеземного эллипсоида.

С целью снижения погрешности определения геодезической долготы объекта геодезическую долготу объекта определяют по величинам отношений тех компонентов вектора положения объекта в геоцентрической системы координат, которые соответствуют осям, лежащим в экваториальной плоскости общеземного эллипсоида, к модулю проекции данного вектора на упомянутую плоскость.

Предлагаемое изобретение позволяет определять геодезические координаты объекта с более высокой точностью.

Применение предлагаемого способа иллюстрируется чертежом, на котором в декартовой геоцентрической системе координат показаны векторы:

- положения навигационного комплекса;

- положения устройства определения положения объекта относительно упомянутого навигационного комплекса;

- положения объекта относительно устройства определения положения объекта;

- положения объекта в известном способе;

- положения объекта в предлагаемом способе;

- погрешности определения положения объекта известным способом.

Предлагаемый способ определения геодезических координат объекта заключается в следующем.

1. Измеряют геодезические координаты L_A, B_A, H_A размещенного на носителе навигационного комплекса и с помощью размещенного на упомянутом носителе устройства определения положения объекта - вектор положения объекта относительного упомянутого устройства.

2. Дополнительно измеряют вектор положения упомянутого устройства относительно упомянутого навигационного комплекса и угловую ориентацию ϑ, γ, ψ_к носителя относительно земли.

Измерение вектора положения упомянутого устройства относительно упомянутого навигационного комплекса и угловой ориентации ϑ, γ, ψ_к носителя относительно земли является существенным признаком изобретения, поскольку необходимо для исключения методической погрешности (11) определения геодезических координат объекта.

3. По измеренным данным вычисляют в декартовой геоцентрической системе координат компоненты вектора положения навигационного комплекса

где - вспомогательная переменная,

и в этой же системе координат вычисляют компоненты вектора положения объекта относительно упомянутого устройства

где , , - компоненты упомянутого вектора положения объекта в нормальной СК.

4. Дополнительно в декартовой геоцентрической системе координат вычисляют компоненты вектора положения упомянутого устройства относительно упомянутого навигационного комплекса

где

- компоненты вектора положения в нормальной системе координат.

5. Определяют в декартовой геоцентрической системе координат вектор положения объекта суммированием вычисленных упомянутых компонент векторов и , дополнительно учитывая компоненты вектора положения устройства относительно навигационного комплекса:

6. По вектору положения объекта определяют геодезические координаты объекта: долготу L, широту В и высоту Н.

С целью снижения погрешности определения геодезической широты В_i+1 объекта при определении геодезических координат объекта по вектору положения объекта геодезическую широту находят путем приближений ее значений. Предлагаются 2 варианта.

Вариант 1. Геодезическую широту В объекта определяют уточнением как минимум один раз приближенного значения ее тангенса t путем вычитания корректирующей поправки Δt, т.е.

Поправка Δt равна отношению значения функции

к скорости изменения этой функции (т.е. к производной этой функции по t), при значении t, равном предшествующему приближенному его значению t_i, т.е.

Функция F(t) представляет собой левую часть уравнения (3), связывающего тангенс t геодезической широты с декартовыми геоцентрическими координатами объекта (4)...(5).

Уточнение (12) приближенного значения тангенса t_i путем введения корректирующей поправки (14) основано на численном решении нелинейного уравнения методом Ньютона [Самарский А.А., Гулин А.В. Численные методы: Учебное пособие - М.: Наука. Гл. ред. физ.-мат. лит., 1989, с.193]. Известно [там же, с.200], что сходимость метода Ньютона существенно более быстрая, чем метод простой итерации (6), использованный в известном способе.

Начальное приближенное значение тангенса t_i геодезической широты определяют по тангенсу t₀ геоцентрической широты объекта из уравнения (3) по формуле

Данное определение начального приближенного значения тангенса геодезической широты обеспечивает более высокую точность определения геодезической широты объекта вследствие использования уравнения связи (3) геодезической широты объекта с компонентами вектора положения объекта в декартовой геоцентрической СК.

Вариант 2. Геодезическую широту В определяют уточнением как минимум один раз ее приближенного значения путем вычитания корректирующей поправки ΔВ

Поправка ΔВ пропорциональна отношению значения функции

к производной этой функции по В (скорости изменения ) при значении В, равном предшествующему приближенному ее значению, т.е.

Выражение (16) получено из уравнения связи геодезической широты с декартовыми геоцентрическими координатами объекта при условии

Операция (15) уточнения приближенного значения геодезической широты B_i путем введения корректирующей поправки ΔВ (17) также представляет собой численное решение нелинейного уравнения (18) методом Ньютона. Уравнение (18) имеет следующий вид:

где

Здесь R - модуль вектора положения объекта в декартовой геоцентрической системе координат.

Уравнение (19) получено преобразованием уравнения (3) с целью снижения погрешности определения геодезической широты В объекта (t стремится по модулю к бесконечности при стремлении В к ). Это уравнение не содержит особенностей во всем диапазоне возможных значений геодезической широты.

Использование функции (16) для уточнения приближенного значения геодезической широты B_i путем введения корректирующей поправки ΔВ (17) обеспечивает повышение точности определения геодезической широты объекта.

Начальное приближенное значение В_i геодезической широты определяют по геоцентрической широте Ф объекта из уравнения (19) по формуле

Данное определение начального приближенного значения геодезической широты обеспечивает более высокую точность определения геодезической широты объекта вследствие использования уравнения связи (19) геодезической широты объекта с компонентами вектора положения объекта в декартовой геоцентрической системе координат.

В предлагаемом способе геоцентрическую широту Ф объекта определяют согласно (20)...(22) по величинам отношений проекции вектора положения объекта на ось вращения общеземного эллипсоида (компонента ) и модуля R_h проекции этого вектора на экваториальную плоскость общеземного эллипсоида к модулю R этого вектора.

Известное более простое определение геоцентрической широты объекта Ф, например только по отношению проекции вектора положения объекта на вертикальную ось декартовой геоцентрической СК к модулю R вектора положения объекта (20)

приводит к неограниченному возрастанию погрешностей δФ ее вычисления вблизи значений . Действительно, из выражения (24) следует для погрешности геоцентрической широты

В свою очередь согласно выражению (20) справедливо

Из выражений (25) и (26) следует, что малейшие погрешности определения вектора положения объекта приводят к неограниченному возрастанию погрешности определения геоцентрической широты Ф объекта, а следовательно, согласно (23) и его геодезической широты В_i. Поэтому предлагаемое определение геоцентрической широты Ф объекта обеспечивает повышение точности определения геодезической широты объекта.

С целью снижения погрешности геодезическую высоту Н объекта определяют по формуле

где - компонент вектора положения объекта в декартовой геоцентрической системе координат по оси вращения общеземного эллипсоида [ГОСТ Р 51794-2001. Государственный стандарт Российской Федерации. Аппаратура радионавигационная глобальной навигационной спутниковой системы и глобальной системы позиционирования. Системы координат. Методы преобразований координат определяемых точек. - М.: Госстандарт России, с.3...4].

Определение геодезической высоты Н по (27) обеспечивает повышение точности определения геодезической высоты объекта при любых возможных значениях геодезической широты В в отличие от известного способа.

С целью снижения погрешности геодезическую долготу L объекта определяют величинами отношений тех компонентов вектора положения объекта в геоцентрической системы координат, которые соответствуют осям, лежащим в экваториальной плоскости общеземного эллипсоида, к модулю проекции R_h данного вектора на упомянутую плоскость. Эти

L=L_A+l.

Предлагаемый способ (28)...(30) определения приращения l геодезической долготы объекта содержит особенность типа 0/0 только при значении R_h=0 (28, 29), которое соответствует нахождению объекта над одним из полюсов ОЗЭ. Но в полюсах значение геодезической долготы изначально не определено, поэтому при значении R_h=0 для приращения геодезической долготы объекта можно положить l=0.

Определение приращения l геодезической долготы объекта по величинам отношений компонентов , R_h вектора положения объекта по осям геоцентрической системы координат в экваториальной плоскости общеземного эллипсоида к модулю R проекции данного вектора на упомянутую плоскость обеспечивает повышение точности определения геодезической широты объекта.

Предлагаемое изобретение позволяет определять геодезические координаты объекта с более высокой точностью, поскольку исключает методические погрешности определения геодезических координат объекта известным способом.

1. Способ определения геодезических координат объекта, при котором измеряют геодезические координаты размещенного на носителе навигационного комплекса и с помощью размещенного на упомянутом носителе устройства определения положения объекта - вектор положения объекта относительно упомянутого устройства, по измеренным данным вычисляют в декартовой геоцентрической системе координат компоненты вектора положения объекта относительно упомянутого устройства и вектора положения навигационного комплекса и определяют в этой системе координат вектор положения объекта суммированием вычисленных упомянутых компонент, по вектору положения объекта определяют геодезические координаты объекта, отличающийся тем, что дополнительно измеряют вектор положения упомянутого устройства относительно упомянутого навигационного комплекса и угловую ориентацию носителя относительно земли, при упомянутом вычислении компонент в декартовой геоцентрической системе координат дополнительно вычисляют компоненты упомянутого вектора положения упомянутого устройства относительно упомянутого навигационного комплекса и дополнительно их учитывают при упомянутом суммировании.

2. Способ по п.1, отличающийся тем, что геодезическую широту объекта определяют уточнением как минимум один раз приближенного значения ее тангенса t путем вычитания корректирующей поправки, равной отношению значения функции

где t₀ - тангенс геоцентрической широты объекта,

е - эксцентриситет общеземного эллипсоида,

а - большая полуось общеземного эллипсоида,

R_h - модуль проекции вектора положения объекта на экваториальную плоскость общеземного эллипсоида,

к производной этой функции по t при значении t, равном предшествующему приближенному его значению.

3. Способ по п.2, отличающийся тем, что начальное приближенное значение тангенса t геодезической широты определяют по тангенсу t_o геоцентрической широты объекта по формуле

4. Способ по п.1, отличающийся тем, что геодезическую широту В объекта определяют уточнением как минимум один раз ее приближенного значения путем вычитания корректирующей поправки, равной отношению значения функции

где Ф - геоцентрическая широта объекта,

R - модуль вектора положения объекта,

к производной этой функции по В при значении В, равном предшествующему приближенному ее значению.

5. Способ по п.4, отличающийся тем, что начальное приближенное значение геодезической широты В определяют по геоцентрической широте Ф объекта по формуле

6. Способ по п.5, отличающийся тем, что геоцентрическую широту Ф объекта определяют по величинам отношений проекции вектора положения объекта на ось вращения общеземного эллипсоида и модуля проекции этого вектора на экваториальную плоскость общеземного эллипсоида к модулю этого вектора.

7. Способ по любому из пп.1-6, отличающийся тем, что геодезическую высоту Н объекта определяют по формуле

где - компонент вектора положения объекта в декартовой геоцентрической системе координат, параллельный оси вращения общеземного эллипсоида.

8. Способ по любому из пп.1-6, отличающийся тем, что геодезическую долготу объекта определяют по величинам отношений тех компонентов вектора положения объекта в геоцентрической системе координат, которые соответствуют осям, лежащим в экваториальной плоскости общеземного эллипсоида, к модулю проекции данного вектора на упомянутую плоскость.

9. Способ по п.7, отличающийся тем, что геодезическую долготу объекта определяют по величинам отношений тех компонентов вектора положения объекта в геоцентрической системе координат, которые соответст