Способ интегрирующего аналого-цифрового преобразования напряжения

Способ интегрирующего аналого-цифрового преобразования напряжения

Иллюстрации

Показать все

Реферат

В настоящее время самые высокоточные АЦП напряжения строятся на принципе промежуточного компенсационного интегрирующего преобразования напряжения в сигнал одного из видов импульсной модуляции - ШИМ, ЧИМ, ФИМ, ИРМ (импульсно-разностной модуляции), КИМ (кодоимпульсной модуляции). Промежуточный сигнал суммируют в течение времени преобразования, во много раз превышающего период импульсной модуляции. Чем больше время преобразования, тем потенциально более высокая разрешающая способность может быть достигнута. Однако на этом пути есть серьезные ограничения, связанные с рядом методических и инструментальных погрешностей, из которых одной из основных является так называемая погрешность от краевых эффектов.

Наиболее высокая точность интегрирующих АЦП (ИАЦП) достигнута при использовании ИРМ. Ряд иностранных фирм, в том числе ANALOG DEVICES, BURR-BROWN, INTERSIL, TEXAS INSTRUENTS и другие, освоили массовый выпуск в интегральном исполнении ИАЦП с разрешением от 8 до 24 двоичных разрядов в интегральном исполнении [1, 2]. В зарубежной литературе такие ИАЦП принято называть ΣΔ-АЦП (в некоторых источниках ΔΣ-АЦП).

Предлагаемое изобретение направлено на устранение погрешности ИАЦП от краевых эффектов. Поэтому рассмотрим природу этой погрешности на двух примерах.

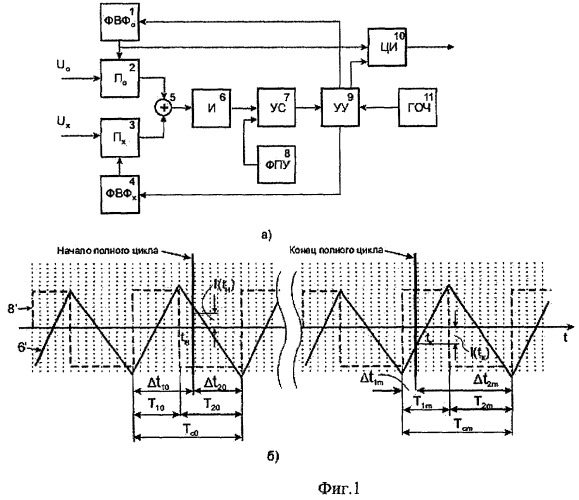
На фиг.1,а представлена обобщенная функциональная схема ИАЦП, в которой может быть реализован любой вид импульсной модуляции [3]. В состав схемы входят следующие узлы: 1 - формирователь весовой функции g_o(t), 2 - перемножитель опорного напряжения U_o на весовую функцию g_o(t), 3 - перемножитель преобразуемого напряжения U_x на весовую функцию g_x(t), 4 - формирователь весовой функции g_x(t), 5 - сумматор, 6 - интегратор, 7 - устройство сравнения, 8 - формирователь порогового уровня, 9 - устройство управления, 10 - цифровой интегратор (счетчик импульсов), 11 - генератор тактовой частоты. Процессы, происходящие в ИАЦП, поясняются временной диаграммой на фиг.1,а. Конкретный вид диаграммы зависит от вида импульсной модуляции, реализуемой в ИАЦП. В данном случае реализуется фазоимпульсная модуляция. Формирователь порогового уровня 8 изменяет полярность порогового напряжения (на диаграмме соответствующая осциллограмма обозначена как 8') всякий раз, как выходное напряжение интегратора 6 (на диаграмме оно обозначено как 6') достигает порогового уровня. Однако это происходит не сразу после срабатывания устройства сравнения 7, а в момент прихода первого после срабатывания импульса тактовой частоты. Эти моменты отмечены на диаграмме вертикальными прямыми, изображенными в виде точек. Весовая функция g_o(t) синхронно с изменением порогового уровня меняет знак своего значения (по модулю оно равно единице), в результате чего изменяется полярность опорного напряжения, поступающего на вход сумматора 5 с выхода перемножителя 2.

Уравнение преобразования может быть представлено в следующем виде:

где u_x(t) - преобразуемое напряжение; U_o - опорное (образцовое) напряжение; τ_х и τ_о - постоянные времени интегратора 6 со стороны преобразуемого и опорного напряжений соответственно; g_x(t) и g_o(t) - весовые функции; t_н и t_к - моменты начала и конца интервала интегрирования (времени преобразования); I(t_н) и I(t_к) - значения выходной величины интегратора в начале и конце времени преобразования ИАЦП.

Как показано в работе [3], весовая функция g_x(t) определяет динамические свойства ИАЦП, так как в ряде случаев (когда она четно- или нечетно-симметрична относительно интервала интегрирования) она полностью эквивалентна импульсной переходной функции, а во всех остальных случаях (g_x(t) несимметрична) динамические свойства ИАЦП определяются импульсной переходной функцией, которая связана с весовой функцией простым соотношением - она зеркально симметрична по отношению к весовой функции (в математике подобные функции называют энантиаморфными). Для простоты в рассматриваемом алгоритме весовая функция g_x(t) имеет постоянное значение, равное 1, в результате чего ИАЦП имеет амплитудно-частотную характеристику вида |Sinω(t_к-t_н)/ω(t_к-t_н)| [3], где ω - частота входного воздействия. Как известно, такая АЧХ имеет нули на частотах, кратных частоте 1/(t_к-t_н), что обеспечивает подавление помех с частотами, равными и кратными этой частоте.

Наличие в правой части уравнения (1) разности I(t_к)-I(t_н) и является источником погрешности, которую принято называть погрешностью от краевых эффектов. На выходе цифрового интегратора 10 формируется результат преобразования, выражаемый следующим соотношением, получающимся путем разрешения уравнения (1) относительно выходной величины

где ΔI=I(t_к)-I(t_н); ΔIτ_o/U_o - абсолютное значение погрешности от краевых эффектов.

Погрешность от краевых эффектов неизбежна при реализации любых известных алгоритмов интегрирующего развертывающего преобразования с промежуточным преобразованием в сигнал импульсной модуляции. Например, существуют алгоритмы преобразования напряжения в ШИМ сигнал, которые в статике обеспечивают значение ΔI=0, однако в динамике ΔI≠0.

Выше указывалось, что на сегодняшний день наивысшей точностью преобразования обладают ΣΔ-АЦП. Это достигнуто благодаря принятым в них мерам по уменьшению погрешности от краевых эффектов. Рассмотрим один из примеров ΣΔ-АЦП.

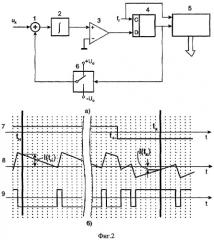
На фиг.2 представлена функциональная схема простейшей разновидности ΣΔ-АЦП [1]. Схема включает сумматор 1, интегратор 2, устройство сравнения 3 выходного напряжения интегратора 2 с нулевым уровнем, тактируемый триггер 4, цифровой фильтр 5, на выходе которого формируется результат преобразования, и переключатель 6 полярности опорного напряжения U_o. Алгоритм преобразования поясняется временной диаграммой на фиг.2,б. Всякий раз, как выходное напряжение интегратора пересекает нулевой уровень, происходит переключение полярности опорного напряжения в первый после срабатывания устройства сравнения тактируемый момент времени. Эти моменты на диаграмме показаны точечными вертикальными прямыми. Для лучшего понимания работы ИАЦП на диаграмме фиг 2,б в момент t_+- происходит смена полярности преобразуемого напряжения (осциллограмма 7). Как и в ранее рассмотренном алгоритме, имеет место не равное нулю значение разности ΔI=I(t_к)-I(t_н), что является источником погрешности от краевых эффектов. Эта погрешность уменьшается (практически почти исключается) за счет применения цифровой фильтрации на этапе получения цифрового эквивалента выходной величины ИАЦП. Наличие цифрового фильтра существенно усложняет схемную реализацию ИАЦП, хотя при современном уровне технологии интегральных микросхем этот недостаток не считается очень существенным (цифровой фильтр реализуется с использованием ПЛМ). Тем не менее, любое упрощение схемы повышает ее надежность. Поэтому независимо от уровня развития технологии более простые технические решения всегда будут предпочтительными.

Предлагаемое изобретение направлено на исключение погрешности от краевых эффектов с использованием способа, обеспечивающего упрощение алгоритма и схемной реализации ИАЦП. Это достигается за счет того, что в процессе интегрирующего аналого-цифрового преобразования напряжения, основанного на интегрировании разности входного напряжения и промежуточного сигнала, получаемого с помощью импульсной модуляции - путем переключения в тактируемый момент времени полярности опорного напряжения при пересечении интегралом указанной разности порогового уровня, и на получении цифрового эквивалента преобразуемого напряжения путем счета импульсов опорной частоты, заполняющих импульсы промежуточного сигнала, при этом основной результат преобразования получают как цифровой эквивалент промежуточного сигнала в течение части времени преобразования, которая состоит из периодов импульсной модуляции, полностью укладывающихся в интервал времени преобразования, а цифровые эквиваленты промежуточных сигналов за периоды импульсной модуляции, приходящиеся на начало и конец времени преобразования, умножают на относительное значение части периода импульсной модуляции, находящейся в пределах времени преобразования, и прибавляют полученные произведения к основному результату.

Для пояснения предлагаемого способа коррекции погрешности от краевых эффектов обратимся к временной диаграмме на фиг.1,б. Без учета 0-го и m-го периодов, которые приходятся на моменты начала t_н и конца t_к времени преобразования, результат преобразования может быть представлен как

где Δt_1...m-1 - погрешность квантования.

Формула (3) выражает результат преобразования без погрешности от краевых эффектов, он содержит лишь погрешность квантования, которая существенно меньше погрешности от краевых эффектов. Но нас интересует полный результат преобразования за весь интервал интегрирования t_к-t_н. Для этого определим результаты преобразования Т₀ и Т_m соответственно в 0-м и m-м периодах импульсной модуляции, приходящихся на начало и конец времени преобразования. Получим:

где Δt₀ и Δt_m - погрешности квантования.

Очевидно, что скорректированный результат преобразования выражается следующим соотношением:

Каждое из слагаемых правой части содержит погрешность квантования, причем во втором и третьем слагаемом эти погрешности входят с весами Δt₂₀/(Δt₁₀+Δt₂₀)<=1 и Δt_1m/(Δt_1m+Δt_2m)<=1. Максимальное значение абсолютной погрешности квантования равно одному периоду тактовой частоты. Следовательно, в самом худшем случае погрешность скорректированного результата не может превысить три кванта. Однако вероятность сочетания факторов, определяющих такое значение результирующей погрешности, весьма и весьма мала. Нужно учитывать, что не только значения, но и знаки всех трех составляющих являются случайными, что приводит к их взаимной компенсации. Результаты модельного эксперимента, проведенного с использованием пакета Simulink программного комплекса MATLAB, показали, что среднеквадратическое значение результирующей погрешности не превышает 0,498 кванта, с доверительной вероятностью 0,99 погрешность не превышает ±0,9 кванта.

Что касается реализации, то она особенно упрощается, если использовать алгоритмы, при которых обеспечивается неизменность периода импульсной модуляции (т.е. Δt_1i+Δt_2i=Const). В этом случае исключаются операции деления при вводе поправки по формуле (6).

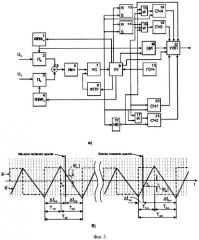
Один из возможных вариантов функциональной схемы устройства, реализующего предлагаемый способ, представлен на фиг.3,а. В состав схемы входят основные блоки, типичные для ИАЦП без ввода поправки, и дополнительные блоки, предназначенные для ввода поправки с целью исключения погрешности от краевых эффектов. К основным блокам относятся: 1 - формирователь весовой функции g_o(t), 2 - перемножитель опорного напряжения U_o на весовую функцию g_o(t), 3 - перемножитель преобразуемого напряжения U_x на весовую функцию g_x(t), 4 - формирователь весовой функции g_x(t), 5 - сумматор, 6 - интегратор, 7 - устройство сравнения, 8 - формирователь порогового уровня, 9 - устройство управления, 10 - цифровой интегратор (счетчик импульсов), 11 - генератор тактовой частоты. Дополнительными являются блоки: логическая схема НЕ 12, RS-триггеры 13 и 14, логические схемы И 15, 16, 17, счетчики импульсов 18, 19, 20, 21 и устройство ввода поправки 22. Согласно временной диаграмме фиг.3,б процесс получения промежуточного сигнала импульсной модуляции осуществляется следующим образом. Под действием разности преобразуемого напряжения и опорного напряжения с выхода формирователя 1 напряжение на выходе интегратора 6 линейно (рассматриваем случай преобразования постоянного напряжения) возрастает или убывает. Когда выходное напряжение интегратора достигает порогового уровня, то срабатывает устройство сравнения 7 и в момент первого пришедшего после этого тактового импульса по команде устройства управления происходит смена полярности порогового напряжения (на выходе блока 8) и опорного напряжения (на выходе блока 1). Цифровой эквивалент основного результата преобразования получают путем счета цифровым интегратором 10 импульсов тактовой частоты, заполняющих положительные импульсы промежуточного сигнала импульсной модуляции, в течение части времени полного цикла за вычетом интервалов Δt₂₀ и Δt_m (см. временную диаграмму фиг.3,б). Соответствующее управляющее воздействие (формирование интервала счета импульсов) осуществляет устройство управления 9. Ввод поправки производится следующим образом. На счетчик 20 непрерывно поступают импульсы с выхода генератора тактовой частоты 11. Счетчик 20 сбрасывается в нуль передним фронтом импульсов с выхода устройства сравнения 7. В результате в момент времени, соответствующий границе между полными циклами, со счетчика может быть взят отсчет цифрового эквивалента интервала Δt₁. На счетчик 21 поступают тактовые импульсы в течение информативных интервалов времени T_1i с выхода логической схемы И 17. Счетчик 21 сбрасывается в нуль задним фронтом импульсов с выхода устройства сравнения 7 (для этого между выходом устройства сравнения 7 и входом схемы И 17 включена логическая схема НЕ 12). В результате в момент времени, соответствующий границе между полными циклами, со счетчика 21 может быть взят отсчет цифрового эквивалента интервала T₁₀. RS-триггер 13 устанавливается в единичное состояние в момент времени, соответствующий границе между полными циклами с выхода устройства управления 9, и сбрасывается в нулевое состояние передним фронтом импульсов с выхода устройства сравнения 7. В результате выходной импульс RS-триггера 13 имеет длительность, равную интервалу Δt₂, а в счетчике 18 получаем цифровой эквивалент этого интервала, так как на вход счетчика тактовые импульсы поступают в течение указанного интервала через схему И 15. Наконец, RS-триггер 14 устанавливается в единичное состояние в момент времени, соответствующий границе между полными циклами с выхода устройства управления 9, и сбрасывается в нулевое состояние передним фронтом импульсов с выхода устройства сравнения 7. На входы логической схемы И 16 поступают тактовые импульсы, а также импульсы с выхода логической схемы НЕ 12. Импульсы с выхода схемы И 16 подсчитываются счетчиком 19, который сбрасывается в нуль каждым передним фронтом импульса с выхода устройства сравнения 7, задержанным на некоторое время, не превышающее периода тактовых импульсов (линия задержки на схеме не показана). В результате в счетчике 18 периодически получаем цифровой эквивалент интервала Т_2i. А нас интересует интервал Т₂₀. Поэтому цифровой код счетчика 19 передается в устройство ввода поправки 22 только один раз за полный цикл, для чего используется задний фронт импульса с выхода RS-триггера 13. Располагая цифровыми эквивалентами необходимых для ввода поправки интервалов времени, устройство ввода поправки 22 вычисляет окончательный результат преобразования в соответствии с формулой (6).

Описываемый способ исключения погрешности от краевых эффектов может быть реализован в любых разновидностях интегрирующих АЦП, в которых используются другие виды импульсной модуляции (ЧИМ, ШИМ, ИРМ, КИМ).

Литература:

1. Никамин В.А. Аналого-цифровые и цифроаналоговые преобразователи. Справочник. М.: Альтекс-А, 2003 г. - 224 с.

2. Губнер Г.Б., Гутников B.C. Применение ΔΣ модуляции в измерительных устройствах. Сб. трудов: Микропроцессорные средства измерения. Санкт-Петебург: 1998 г. - с.3-14.

3. Шахов Э.К., Михотин В.Д. Интегрирующие развертывающие преобразователи. М.: Энергоатомиздат. 1986 г. - 144 с.

Способ интегрирующего аналого-цифрового преобразования напряжения, основанный на интегрировании разности входного напряжения и промежуточного сигнала, получаемого с помощью импульсной модуляции, путем переключения в тактируемый момент времени полярности опорного и порогового напряжений при пересечении интегралом указанной разности порогового уровня, и на получении цифрового эквивалента преобразуемого напряжения путем счета импульсов опорной частоты, заполняющих импульсы промежуточного сигнала, отличающийся тем, что основной результат преобразования получают как цифровой эквивалент промежуточного сигнала в течение части времени преобразования, которая состоит из периодов импульсной модуляции, полностью укладывающихся в интервал времени преобразования, а цифровые эквиваленты промежуточных сигналов за периоды импульсной модуляции, приходящиеся на начало и конец времени преобразования, умножают на относительное значение части периода импульсной модуляции, находящейся в пределах времени преобразования, и прибавляют полученные произведения к основному результату.