Способ измерения поверхностной плотности полного заряда в плоских диэлектриках

Способ измерения поверхностной плотности полного заряда в плоских диэлектриках

Иллюстрации

Показать все

Реферат

Способ относится к электротехническим измерениям, предназначен для измерения параметров остаточного заряжения плоских диэлектриков, а именно поверхностной плотности полного (реального) заряда, поверхностных плотностей эффективных (формальных) зарядов, а также среднего положения (центра распределения) распределенного в плоском диэлектрике заряда.

Способ основан на индуцировании переменного тока в цепи вибрационного конденсатора с заряженным образцом в его зазоре. Физические основы индукционных измерений параметров остаточного заряжения диэлектрических материалов изложены в (Алейников А.Н., Алейников Н.М. Индукционные методы определения параметров остаточного заряжения диэлектрических материалов, "Материаловедение". - М.: Наука и технологии, №3, с.26-33, 2002). Наиболее распространенными индукционными способами являются компенсационные. В компенсационном способе (А.с. SU №1352411, МПК G 01 R 29/12, 1987) исследуемый плоский диэлектрик помещают в зазор вибрационного плоского конденсатора параллельно его обкладкам и, регулируя постоянное напряжение на конденсаторе, добиваются полного исчезновения тока в цепи конденсатора. Затем перемещают образец в другое положение и снова добиваются нулевого тока конденсатора, регулируя напряжение на конденсаторе. Величину поверхностной плотности заряда вычисляют по формуле

где U₁ и U₂ напряжения компенсации, при которых амплитуды токов конденсатора I₁ и I₂ обращаются в нуль, Δ_l - величина перемещения образца из первого положения во второе. Основной недостаток компенсационных измерений определяется необходимостью применения высоких электрических компенсационных напряжений, разрушающих исследуемые электретные состояния.

Наиболее близким к заявленному способу является способ частичной компенсации (А.с. SU №1471152, МПК G 01 R 29/12, 1989) (прототип). В этом способе так же, как и в компенсационном способе, перемещают образец из одного положения в другое и регулируют постоянное напряжение на конденсаторе. Но добиваются не полного исчезновения тока конденсатора, а только равенства токов для обоих положений образца в зазоре конденсатора. Величину σ_r вычисляют по формуле, аналогичной (1).

По сравнению с компенсационными способами в способе-прототипе применяются значительно меньшие напряжения на конденсаторе, не разрушающие исследуемое электретное состояние, что делает этот способ более точным. Недостатком данного способа является необходимость измерения и регулирования напряжения на конденсаторе вплоть до момента выравнивания токов для различных положений образца в зазоре конденсатора. Это делает способ малотехнологичным и ограничивает возможность автоматизации измерений при массовых или длительных измерениях.

Задача, решаемая данным изобретением, - повышение технологичности и расширение функциональных возможностей способа измерения параметров остаточного заряжения диэлектрических материалов.

Технический результат заключается в упрощении процесса измерения исключением регулирования и систематического измерения напряжения на конденсаторе.

Технический результат достигается тем, что в известном способе измерения поверхностной плотности полного заряда в плоских диэлектриках, основанном на индуцировании и измерении переменного тока в цепи вибрационного конденсатора с заряженным образцом в его зазоре, включающем помещение образца в первое положение в зазор конденсатора параллельно его обкладкам и перемещение образца в направлении нормали к его поверхности во второе положение, согласно предлагаемому изобретению измеряют токи конденсатора для обоих положений образца при нулевом напряжении на конденсаторе, а также измеряют ток конденсатора в одном из положений образца, например первом, при известном постоянном напряжении на конденсаторе, а искомую величину плотности заряда вычисляют по формуле

где ε₀=8,85·10^-14 Ф/см - электрическая постоянная, Δl - величина перемещения образца из первого положения образца во второе, U - известное постоянное напряжение, I₁₀ и I₂₀ - сила тока конденсатора для первого и второго положений образца при нулевом напряжении на конденсаторе, I_1U - сила тока конденсатора для первого положения образца при напряжении U на конденсаторе.

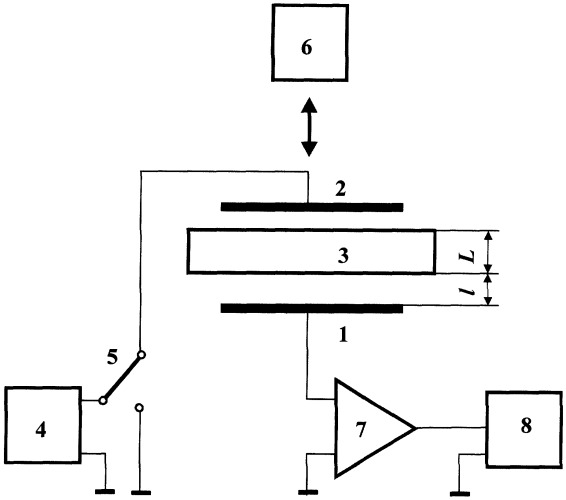
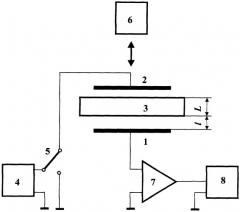
Рассмотрим суть предлагаемого изобретения. На чертеже приведена принципиальная схема, реализующая данный способ. Обкладками измерительного плоского вибрационного конденсатора являются неподвижный 1 и вибрационный 2 электроды. Между плоским образцом 3 толщиной L и электродом 1 образуется воздушный зазор, величина 1 которого может изменяться, например, при помощи микрометрического устройства (на чертеже не показано). От источника 4 при помощи переключателя 5 на обкладки 1 и 2 может подаваться нулевое или известное отличное от нуля постоянное напряжение U. Механические гармонические колебания электрода 2 возбуждаются вибратором 6. Возникающий в цепи конденсатора ток преобразуется усилителем 7 в напряжение, регистрируемое, например, осциллографом 8. Амплитуда переменного тока будет

где А - постоянная величина, зависящая от частоты и амплитуды вибрации, площади обкладок и межэлектродного расстояния вибрационного конденсатора, толщины и диэлектрической проницаемости образца, σ_r - поверхностная плотность полного (реального) заряда, σ_L - поверхностная плотность эффективного (формального) заряда.

Обозначим амплитуду тока в первом положении образца при нулевом напряжении на конденсаторе I₁₀, амплитуду тока во втором положении образца при нулевом напряжении на конденсаторе I₂₀ и амплитуду тока в первом положении образца при напряжении U на конденсаторе I_1U. Тогда в соответствии с (3) получим:

I₁₀=А(εl₁σ_r+Lσ_L), I₂₀=A(εl₂σ_r+Lσ_L), I_1U=A(εl₁σ_r+Lσ_L-ε₀εU).

Решая систему из трех последних уравнений, получим формулу (2) для вычисления σ_r. Из (2) следует, что для определения σ_r необходимо измерить амплитуды токов I₁₀ и I_1U в одном положении образца при нулевом напряжении и известном напряжении U на конденсаторе, переместить образец на величину Δl и в этом положении образца измерить ток I₂₀ при нулевом напряжении на конденсаторе.

В качестве примера сравним возможности компенсационного способа, способа частичной компенсации и заявленного способа. Пусть у плоского образца толщиной L=0,4 см и диэлектрической проницаемостью ε=4 поверхностная плотность полного заряда составляет σ_r=10^-10 Кл/см ². Величины зазоров l₁ и l₂ составляют: l₁=0,1 см, l₂=0,2 см. Для упрощения расчетов предположим, что весь заряд локализован на поверхности образца, обращенной к вибрационному электроду 2, т.е. поверхностная плотность полного (реального) заряда σ_r равна поверхностной плотности эффективного (формального) заряда σ_L.

При измерениях компенсационным способом при l=l₂ потребуется напряжение компенсации:

При измерениях способом частичной компенсации напряжение составит

При измерениях предлагаемым способом точность в определении искомой величины σ_r будет определяться не только точностью измерения токов I₁₀, I₂₀, I_1U, но и относительной величиной I_1U/I₁₀, которая в знаменателе конечной формулы (2) для вычисления σ_r сравнивается с единицей. В частности, при малых значениях напряжения, когда U→0, величина I_1U/I₁₀→1 и вычисления σ_r приводят к бесконечно большому значению. Поэтому напряжение U должно быть достаточным, чтобы величина I_1U/I₁₀ заметно отличалась от единицы. Оценим величину I_1U/I₁₀ для рассматриваемого примера при напряжении U=40 В.

Полученный результат показывает, что для определения σ_r заявленным способом используемое напряжение (40 В) может быть значительно ниже не только напряжения, требуемого при компенсационных измерениях (340 В), но и напряжения, необходимого при измерениях способом частичной компенсации (113 В). При этом относительная величина I_1U/I₁₀≈0,82 достаточно отличима от единицы и на точность измерений существенного влияния не оказывает.

Достоинством заявленного способа по сравнению со способом-прототипом является также возможность по полученным результатам измерений определить среднее положение распределенного в диэлектрике заряда

Методика определения рассмотрена в первом аналоге и [1], [2]. Кроме того, зная σ_r и можно определить и другие параметры остаточного заряжения, а именно поверхностные плотности σ_L и σ₀ приведенных к обеим поверхностям плоского образца эффективных (формальных) зарядов:

Необходимо отметить, что возможны случаи, когда при перемещении образца из положения l₁ в положение l₂ или при изменении напряжения от нулевого до известного напряжения U начальная фаза колебаний тока конденсатора изменится на противоположную. В таких случаях, как показано в первом аналоге и [2] при вычислении σ_r и величины I₂₀/I₁₀ или I_1U/I₁₀ нужно брать отрицательными.

Использованные источники информации:

1. А.с. SU №1688199, МПК G01R 29/12, 1991.

2. Патент RU №2231804, МПК G01R 29/12, 2004.

Способ измерения поверхностной плотности полного заряда в плоских диэлектриках, основанный на индуцировании и измерении переменного тока в цепи вибрационного конденсатора с заряженным образцом в его зазоре, включающий помещение образца в первое положение в зазор конденсатора параллельно его обкладкам и перемещение образца в направлении нормали к его поверхности во второе положение, отличающийся тем, что измеряют токи конденсатора для обоих положений образца при нулевом напряжении на конденсаторе, а также измеряют ток конденсатора в одном из положений образца, например первом, при известном постоянном напряжении на конденсаторе, а искомую величину плотности заряда вычисляют по формуле

где ε₀=8,85·10^-12 Ф/м - электрическая постоянная;

Δl - величина перемещения образца из первого положения образца во второе;

U - известное постоянное напряжение;

I₁₀ и I₂₀ - сила тока конденсатора для первого и второго положений образца при нулевом напряжении на конденсаторе;

I_1U - сила тока конденсатора для первого положения образца при напряжении U на конденсаторе.