Устройство для преобразования из полиномиальной системы классов вычетов в позиционный код с пересчетом ортогональных базисов
Иллюстрации
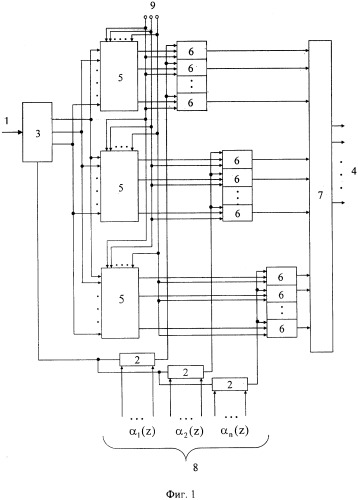
Показать всеИзобретение относится к вычислительной технике и, в частности, к модулярным спецпроцессорам (СП), функционирующим в полиномиальной системе классов вычетов (ПСКВ) и способным сохранять работоспособное состояние при возникновении ошибки за счет реконфигурации структуры. Технический результат - возможность вычисления значений ортогональных базисов при возникновении отказов вычислительных трактов по модулю pi(z) и их исключении из процесса преобразования модулярного кода ПСКВ в двоичный позиционный код. Технический результат достигается за счет ввода в конструкцию группы блоков расчета ортогональных базисов и сумматора по модулю два. Устройство содержит вход (1) запуска устройства, группу сдвиговых регистров (2), блок (3) синхронизации; выход (4) устройства, группу блоков (5) расчета ортогональных базисов, блоки (6) трехвходовых элементов И, сумматор (7) по модулю два, группу информационных входов (8), группу управляющих входов (9) устройства. 1 з.п. ф-лы, 2 ил., 1 табл.
Реферат
Изобретение относится к вычислительной технике и, в частности, к модулярным спецпроцессорам (СП), функционирующим в полиномиальной системе классов вычетов (ПСКВ) и способным сохранять работоспособное состояние при возникновении ошибки за счет реконфигурации структуры.
Известно устройство для преобразования числа из системы остаточных классов в позиционный код (Авторское свидетельство №1501280, кл. Н03М 7/18, 15.08.89. Бюл. №30), которое содержит вход запуска устройства, группу информационных входов, группу сдвиговых регистров, блок синхронизации, группу блоков памяти, блоки элементов И, накапливающий сумматор, выход устройства.
Недостатком данного устройства является неспособность сохранять работоспособное состояние при возникновении отказов (дефектах аппаратуры) и, следовательно, невозможность работы спецпроцессора в режиме постепенной деградации.
Техническим результатом изобретения является расширение функциональных возможностей, проявляющееся в возможности вычисления значений ортогональных базисов при возникновении отказов вычислительных трактов по модулю pi(z) и их исключении из процесса преобразования модулярного кода ПСКВ в двоичный позиционный код.
Указанный технический результат достигается за счет ввода в конструкцию группы блоков расчета ортогональных базисов и сумматора по модулю два.
Устойчивость структуры вычислительного устройства к дефектам аппаратуры обеспечивает возможность работы спецпроцессора в режиме постепенной деградации. Указанное свойство обеспечивает высокую живучесть СП и является одним из основных факторов, на которых базируются разработки способов построения систем, способных деградировать постепенно. Применение полиномиальной системы классов вычетов позволяет реализовать построение живучих вычислительных систем с постепенной деградацией структуры.
Говоря о построении живучих непозиционных вычислительных систем, базирующихся на модулярном представлении чисел, в первую очередь надо отметить присущее данным устройствам свойство - способность сохранить работоспособное состояние при возникновении отказов за счет снижения в допустимых пределах основных показателей качества функционирования.
Одним из основных достоинств модулярных кодов, к которым относится и ПСКВ, являются обменные операции. Алгоритмической основой обменных операций между точностью, производительностью и корректирующими способностями являются независимость обработки информации по каждому модулю и функциональная равноправность разрядов. Данные свойства обусловлены полной арифметичностью кодовых конструкций, базирующихся на модулярном представлении чисел, где информационная и контрольные части равноправны относительно любой модульной операции.
Согласно общей теории кодирования мощность модулярного кода определяется соответствием каждому действительному операнду A(z) множества М, A(z)∈М слова (α1(z), α2(z) ... αn(z))∈Рполн(z), где Рполн(z) - декартово произведение некоторых оснований множества, p1(z), p2(z), ..., pn(z); αi(z)∈pi(z); i=1, 2, ..., n. Если на диапазон возможного изменения кодируемого множества M(z) наложить ограничения, считая, что для однозначного представления достаточно k первых остатков (k<n), то соответствующие им основания упорядоченной системы классов вычетов p1(z), p2(z), ..., pk(z); i=1, 2, ..., k принадлежат множеству информационных модулей. В этом случае диапазон однозначного представления по данным основаниям соответственно равен
Оставшиеся r=n-k "лишних остатка" можно считать избыточными, так как их исключение из модульной кодовой конструкции (α1(z), α2(z), ..., αn(z)) не влечет за собой ущерба однозначности представления числа A(z), то есть при отказе r каналов их можно просто удалить из процессора, не оказывая влияния на точность выполнения задания. Но, с другой стороны, данные r избыточных каналов предопределяют корректирующие способности вычислительной системы, другими словами - гарантию защиты от недостоверного результата.
Таким образом, изменяя количество информационных k и избыточных r оснований в заданной структуре непозиционного СП, можно варьировать его основными показателями - точностью, информационной надежностью и производительностью вычислительной системы.
Для перевода числа из полиномиальной системы классов вычетов позиционный код используется китайская теорема об остатках (КТО), согласно которой
где Bi(z) - ортогональный базис i-го основания.
Ортогональный базис определяется как
где mi(z) - вес ортогонального базиса i-го основания.
Применение mi(z) позволяет обеспечить выполнение условия
Bi(z)≡1modpi(z).
Преобразуем выражение (2) к виду
Подставив равенство (3) в выражение (1), получаем
Разделив обе части последнего равенства на величину , получаем
Принимая во внимание попарную простоту модулей pi(z), i=1, 2, ..., k+r, введем обозначение
Тогда
Таким образом, очевидно, что величина веса ортогонального базиса определяется произведением величин, обратных основаниям ПСКВ pj(z) по модулю pi(z).
Следовательно, для пересчета ортогональных базисов при построении деградируемого СП ПСКВ необходимо использовать значения , т.е. обратных величин оснований pj(z) по модулю рi(z) для поля GF(24). В таблице представлены величины для поля GF(24).
| ТаблицаВеличины для поля GF(24) | |||||
| Значение рi(z) основания ПСКВ | |||||
| p1(z) | p2(z) | p3(z) | p4(z) | p5(z) | |
| - | 1 | 1 | 1 | 1 | |
| z | - | z | z+1 | 1 | |
| z3+z | z3+1 | - | z2+1 | z3+z2+1 | |
| z3 | z3+z2+z | z2 | - | z3+z+1 | |
| z3+z2+z | z2+z | z3+z | z3+z2 | - |
Устройство содержит вход 1 запуска устройства, группу сдвиговых регистров 2, блок 3 синхронизации, выход 4 устройства, группу блоков 5 расчета ортогональных базисов, блоки 6 трехвходовых элементов И, сумматор 7 по модулю два, группу информационных входов 8, группу управляющих входов 9 устройства. Структура устройства показана на фиг.1.
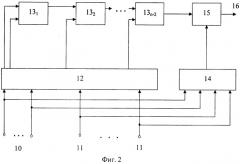
Блок расчета ортогональных базисов содержит синхровход 10, n управляющих входов 11, первый блок памяти 12, (n-2) умножителей 13 по модулю pi(z), где i=1, 2, ..., n, второй блок памяти 14, умножитель 15, выход 16 блока. Структура блока показана на фиг.2.
Устройство работает следующим образом. Если i-й канал модулярного вычислительного устройства является работоспособным, то по соответствующему входу группы управляющих входов 9 поступает значение 1, в противном случае - значение 0.
Число, представляемое в коде ПСКВ, A(z)=(α1(z), α2(z), ..., αn(z)), через группу информационных входов 8 заносится на сдвиговые регистры 2 группы, причем вычеты по каждому из оснований ПСКВ заносятся в свой регистр 2. Работа устройства происходит по тактам. В каждом такте содержимое регистров 2 сдвигается вправо (в сторону младших разрядов) на один разряд. Алгоритм работы устройства может быть представлен в виде
где n - количество оснований ПСКВ;
ni=ordpi(z) - степень i-го основания ПСКВ;
- значение g-го разряда, i-го основания ПСКВ;
- пересчитанное значение i-го ортогонального базиса.
Из выражения (6) видно, что устройство реализует операцию последовательного суммирования произведений пересчитанных ортогональных базисов назначения остатка αi(z), представленного в двоичном коде.
Группа блоков 5 осуществляет расчет ортогональных базисов в соответствии со значениями, поданными на n управляющих входов 9 устройства.
В первом такте по сигналу из блока 3 синхронизации производится выдача величины из блоков 5 параллельно и в случае открытых блоков трехвходовых элементов И группы 6 - прибавление их к содержимому сумматора 7, работающего по модулю два. В следующем такте содержимое каждого из регистров 2 сдвигается на один разряд вправо, и блок 3 синхронизации разрешает выдачу очередного пересчитанного значения из блоков 5.
Работа устройства осуществляется в течение s тактов, где s=ν, для расширенного поля Галуа GF(2ν).
Блок 5 расчета ортогональных базисов групп работает следующим образом. При поступлении первого синхросигнала от блока 3 синхронизации на вход 10 из первого блока памяти 12 на входы первого умножителя 13 по модулю pi(z) подаются два значения . Полученный результат произведения поступает на первый вход второго умножителя 13 по модулю pi(z), на второй вход которого с первого блока памяти 12 подается очередное значение . Полученный результат произведения поступает на первый вход третьего умножителя 13 по модулю pi(z), на второй вход которого с первого блока памяти 12 подается очередное значение . Спустя (n-2) такта на входе (n-2)-го умножителя 13 по модулю pi(z) появляется значение веса ортогонального базиса mi(z). Таким образом, за (n-2) такта определяется значение
Причем величины определяются значением сигнала, поступающего с j-го управляющего входа 11, согласно условию
Значения , поступающие с первого блока 12 памяти, определяются значениями сигналов, подающихся на адресные входы блока 12 с управляющих входов 11 и синхровходов 10.
Причем
где yj - сигнал на j-м входе управляющих входов 11.
Вычисленное значение веса ортогонального базиса по i-му основанию согласно выражения (7) поступает на первый вход умножителя 15, на второй вход которого с выходов второго блока 14 памяти подается значение
где l∉Uотк; Uотк - множество отказавших оснований в процессе функционирования вычислительной системы ПСКВ; g=0, 1, ..., ord pi(z)-1.
Полученное значение P*(z) определится значением сигнала, поступающего на адресные входы второго блока 14 памяти с управляющих входов 11 и синхровходов 10. Во втором блоке 14 памяти хранятся константы произведения zg·P*(z).
Умножитель 15 осуществляет вычисление величины ортогонального базиса
Полученное значение ортогонального базиса согласно (11) подается на вход 16, который является выходом блока 5 расчета ортогональных базисов.
Если в процессе функционирования вычислительной системы ПСКВ откажет b-е основание, то на управляющих входах 9 появится сигнал
(y1, ..., yb-1, yb, yb+1, ..., yn)=(1, ..., 1, 0, 1, ..., 1)
Данный сигнал поступает на управляющие входы 11 блоков 5 расчета ортогональных базисов. Под управлением данного сигнала из первого блока 12 памяти значения , (j=1, ..., n, j≠i), a (n-2) умножителей 13 по модулю два вычисляют
где
Под управлением сигналов, поступивших с управляющих входов 11 и синхровходов 10, из второго блока 14 памяти поступают значения, определенные выражением (10). Умножитель 15 реализует выражение (11), где
Одновременно с этим значения (y1, ..., yb-1, yb, yb+1, ..., yn)=(1, ..., 1, 0, 1, ..., 1) подаются на третьи входы 6 элементов И блоков 6. Нулевой сигнал yb=0 производит закрытие элементов И b-го блока 6. Таким образом, значения αb(z)·Bb(z) в получении конечного результата согласно (6) не участвуют, так как на сумматор 7 они не подаются.
Рассмотрим пример.
Необходимо вычислить значения ортогональных базисов полиномиальной системы классов вычетов, задаваемой в поле GF(24).
Согласно (2) определяем значения Pi(z)
P1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
P2(z)=z13+z12+z10+z9+z7+z6+z4+z3+z2+z+1;
P3(z)=z11+z10+z6+z5+z+1;
P4(z)=z11+z10+z9+z8+z6+z4+z3+1;
P5(z)=z11+z8+z7+z5+3+z2+z+1.
Вычислим значения весов ортогональных базисов. Получаем m1(z)=1; m2(z)=z; m3(z)=z3+z; m4(z)=z3, m5(z)=z.
Определим значения ml(z), воспользовавшись равенством (5). Тогда
m1(z)=1; m2(z)=z2(z+1)mod(z2+z+1)=z;
m3(z)=[(z3+z)(z3+1)(z2+1)(z3+z2+1)]mod(z4+z3+z2+z+1)=z3+z;
m4(z)=[z5(z3+z+1)(z3+z2+z+1)]mod(z4+z3+1)=z3;
m5(z)=[(z3+z2+z)(z3+z)(z2+z)(z3+z2)]mod(z4+z+1)=z.
Тогда ортогональные базисы исходной системы ПСКВ составят
| B1(z)=z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+z3+z2+z+1; | m1(z)=1 |
| B2(z)=z14+z13+z11+z10+z8+z7+z5+z4+z2+z; | m2(z)=z |
| B3(z)=z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z; | m3(z)=z3+z |
| B4(z)=z14+z13+z12+z11+z9+z7+z6+z3; | m4(z)=z3 |
| B5(z)=z12+z9+z8+z6+z4+z3+z2+z; | m5(z)=z |
Полученные данные совпадают с контрольным просчетом.
Рассмотрим процедуру постепенной деградации структуры непозиционного процессора ПСКВ. Допустим, что в процессе функционирования отказало последнее основание p5(z)=z4+z+1. Тогда диапазон представления входных данных составит P1234(z)=z11+z8+z7+z5+z3+z2+z+1.
При этом ортогональные базисы и соответствующие им веса для данной деградируемой системы составят
Для пересчета ортогональных базисов определим значения
Осуществив умножение на , получаем пересчет ортогональных базисов в новой системе оснований, которые совпадают с представленными ранее.
Проведем дальнейшую деградацию структуры непозиционного процессора ПСКВ. Допустим, что в процессе дальнейшего функционирования отказало четвертое основание p4(z)=z4+z3+1. Тогда диапазон представления входных данных составит P123(z)=z7+z6+z5+z2+z+1.
При этом ортогональные базисы и соответствующие им веса составят
Для пересчета ортогональных базисов определим значения
Осуществив умножение на соответствующее значение , получаем пересчет ортогональных базисов в новой системе оснований, которые совпадают с представленными ранее.
1. Устройство для преобразования из полиномиальной системы классов вычетов в позиционный код с пересчетом ортогональных базисов, содержащее вход запуска устройства, группу сдвиговых регистров, блок синхронизации, выход устройства, блоки элементов И, группу информационных входов, причем вход запуска устройства соединен с входом запуска блока синхронизации, выход которого соединен с входами разрешения сдвига сдвиговых регистров группы, информационные входы которых являются соответствующими информационными входами группы устройства, выход i-го сдвигового регистра группы соединен с первым входом элемента И i-й группы (i=1, 2, ..., n), отличающееся тем, что устройство дополнительно содержит группу блоков расчета ортогональных базисов, сумматор по модулю два, управляющие входы устройства, причем выходы блока синхронизации подключены к первому входу блоков расчета ортогональных базисов, второй вход которых подключен к управляющим входам устройства, выход i-го блока расчета ортогональных базисов подключены ко второму входу элементов И i-го блока, третьи входы которых соединены с соответствующим управляющим входом группы, выходы элементов И соединены со входами сумматора по модулю два, выход которого является выходом устройства.
2. Устройство по п.1, отличающееся тем, что блок расчета ортогональных базисов содержит синхровходы управляющих входов, первый блок памяти, n-2 умножителей по модулю pi(z), второй блок памяти, умножитель, выход блока, причем синхровходы и управляющие входы подключены к адресным входам первого и второго блоков памяти, первый и второй входы первого умножителя по модулю подключены к первому и второму выходам первого блока памяти, выход первого j-го умножителя по модулю (j=1, 2, ..., n-3) соединен с первым входом (j+1)-го умножителя по модулю, второй вход которого соединен с (j+2)-м выходом первого блока памяти, выход (n-2)-го умножителя по модулю соединен с первым входом сумматора, второй выход которого соединен с выходами второго блока памяти, выход умножителя является выходом блока.