Способ получения трехмерного изображения поверхности по данным бортовой импульсно-доплеровской рлс маловысотного полета

Способ получения трехмерного изображения поверхности по данным бортовой импульсно-доплеровской рлс маловысотного полета

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, а именно к радиолокационным системам наблюдения за поверхностью на базе бортовой импульсно-доплеровской РЛС маловысотного полета, работающей в режиме "доплеровского обужения" диаграммы направленности антенны (ДНА) с электронным сканированием луча.

Получение трехмерных радиолокационных изображений (РЛИ) поверхности (и объектов на поверхности) с помощью бортовой РЛС необходимо для выполнения полетов на малой высоте, например, в условиях гористой местности при отсутствии оптической видимости, когда высота играет существенное значение для получения правильного пространственного изображения поверхности и обхода препятствий по линии полета. Известен способ обзора поверхности и пространства путем построчного сканирования зоны обзора узким лучом РЛС при его последовательном перемещении на ширину ДНА с помощью электронного управления лучом в системах с ФАР (фазированной антенной решеткой), а также в системах с механической перестройкой антенны, который может быть применен при маловысотном полете (Финкельштейн М.И. Основы радиолокации: Учебник для вузов. М.: Радио и связь, 1983. - 536 с., с.436-439; Пат. 2211459 РФ. Способ обзора пространства и сопровождения объектов поверхности при маловысотном полете / Г.Н. Колодько, В.И. Мойбенко, В.К. Клочко (РФ). - Заявка №2001107438. Приоритет 22.03.2001; Самарин О.Ф., Курилкин В.В. Концепция выполнения маловысотного полета летательных аппаратов с помощью автономных БРЛС // Радиотехника, 1998, №4. - С.50-54). При этом формируется плоское РЛИ в координатах азимут - угол места в срезах (элементах разрешения) дальности. Однако разрешающая способность по угловым координатам при таком способе ограничена шириной ДНА и не позволяет получить детальное изображение поверхности. Для повышения разрешающей способности в импульсно-доплеровских РЛС применяется режим синтезирования апертуры антенны (РСА) с помощью узкополосной доплеровской фильтрации отраженного сигнала в каждом элементе разрешения по дальности (Финкельштейн М.И. Основы радиолокации: Учебник для вузов. М: Радио и связь, 1983. - 536 с., с.436-439; Радиолокационные станции с цифровым синтезированием апертуры антенны / А.Н. Антипов, В.Т. Горяинов, А.Н. Кулин и др. Под ред. В.Т. Горяинова. - М.: Радио и связь, 1988. - 304 с.). Это позволяет получать матрицу РЛ-изображения достаточно большого участка поверхности, накрываемой ДНА, в координатах наклонная дальность - доплеровская частота, которая напоминает плоское оптическое изображение. Однако такой режим используется, в основном, при полете на большой высоте, когда высотой поверхности можно пренебречь, а в условиях маловысотного полета режим "доплеровского обужения" дает искаженное изображение рельефной поверхности и не определяет ее высоты.

Наиболее близким по технической сущности является способ получения двумерного (плоского) РЛИ поверхности в режиме узкополосной доплеровской фильтрации (Кондратенков Г.С., Фролов А.Ю. Радиовидение в передней зоне обзора бортовой радиолокационной станции с синтезированной апертурой антенны / Радиотехника, 2004, №1. - С.47-49). Данный способ заключается в следующем.

1. Приемное устройство РЛС включает в себя М стробов дальности (ключей) S₁, S₂, ..., S_M, которые последовательно открываются и пропускают отраженный сигнал u(t), t∈[t₀,t₁], на одном из М промежутков времени [t₀, t₀+I·Δt], Δt=(t₁-t₀)/M, соответствующих М промежуткам дальности [R₀, R₀+I·ΔR], ΔR=(R₁-R₀)/M, в зоне обзора [R₀,R₁], где ΔR - размер элемента разрешения по дальности.

2. Сигнал u(t), t∈[t₀, t₀+I·Δt], при данном положении луча по азимуту и углу места с выхода каждого I-го строба дальности (I=1, 2, ..., М), подается на алгоритм обужения ДНА, который включает в себя N узкополосных J-х фильтров с разделенными полосами частот [f₀, f₀+J·Δf], Δf=(f₁-f₀)/N, на промежутке [f₀,f₁], где Δf - ширина полосы пропускания фильтра.

3. В соответствии с доплеровским эффектом изменение частоты отраженного сигнала пропорционально изменению скорости движения отраженного луча РЛС в зависимости от угла α отклонения луча от вектора скорости движения объекта-носителя РЛС, где угол α связан нелинейной зависимостью с азимутом ϕ. Полосе частот [f₀,f₁] ставится в соответствие угловой промежуток по азимуту [ϕ₀, ϕ₁], длина которого Δϕ=ϕ₁-ϕ₀ определяется шириной ДНА. Приближенно (из-за нелинейной зависимости α и ϕ) можно считать, что при наличии N фильтров промежуток [ϕ₀, ϕ₁] разбивается на N примерно одинаковых частей, и разрешение по азимуту составляет Δϕ/N, т.е. увеличивается в N раз.

4. В каждом J-м фильтре выделяется амплитуда A(I,J) сигнала, которая соответствует спектру J-й полосы пропускания в I-м стробе дальности. Таким образом, на множестве элементов разрешения по дальности (по I-м строкам) и частоте (по J-м столбцам) в зоне данного направления луча формируется матрица радиолокационного изображения А в виде совокупности амплитуд A(I,J), которая далее передается на алгоритмы индикации для отображения на экране индикатора пилота.

Однако такой способ обладает следующими недостатками.

1. Двумерное (плоское) изображение А не дает информации о высоте поверхности, что не позволяет применять этот способ при маловысотном полете.

2. Изображение А соответствует лишь одному положению узкого луча РЛС и не захватывает всей зоны обзора при маловысотном полете.

3. При попытке сканирования лучом РЛС всей зоны обзора по мере изменения угла места луча меняется соответствие между осью частот и азимутальной осью, что приводит к искажению изображения в целом.

Технический результат направлен на получение трехмерного изображения поверхности при маловысотном полете с повышенным пространственным разрешением в зоне обзора.

Технический результат предлагаемого технического решения достигается тем, что способ получения трехмерного изображения поверхности в зоне обзора бортовой РЛС маловысотного полета с электронным сканированием луча и доплеровской селекцией по частоте заключается в создании режима построчного обзора контролируемого участка пространства в сочетании с узкополосной доплеровской фильтрацией принятых сигналов, позволяющей рассечь пространственные элементы разрешения антенны на мелкие части (доплеровские элементы разрешения - ДЭР), и формировании матрицы трехмерного изображения поверхности в виде совокупности амплитуд отраженных сигналов, зафиксированных в ДЭР, при этом за счет быстрого электронного переключения луча РЛС смещают луч по азимуту и углу места построчно на ширину диаграммы направленности антенны в зоне обзора и при каждом положении луча по азимуту и углу места измеряют амплитуду сигнала на выходе J-го фильтра доплеровских частот в I-м элементе разрешения дальности, тем самым получают двумерное изображение поверхности в пределах зоны обзора при каждом положении луча РЛС в виде совокупности амплитуд, отличающийся тем, что для каждой измеренной амплитуды, превышающей порог обнаружения (соответствующей отражению от поверхности), выбирают i, j, k-e элементы дискретизации прямоугольной сетки x_i, y_j, z_k, сферические координаты которых R, ϕ, θ принадлежат области ДЭР, путем проверки системы неравенств:

где R_I, ϕ_J, θ_J - известные сферические координаты центра ДЭР, R_I - дальность, ϕ_J - азимут, θ_J - угол места, ΔR - разрешение по дальности, Δϕ, Δθ, b - известные для каждого положения луча параметры аппроксимации границ ДЭР по углам, и если i, j, k-e элементы дискретизации принадлежат области ДЭР, то запоминают амплитуду данного ДЭР в матрице амплитуд А, а максимальное значение третьей координаты высоты - в матрице Z, затем повторяют эти операции для всех положений луча и тем самым формируют трехмерное изображение поверхности в зоне обзора РЛС в виде двумерных матриц А и Z.

Способ осуществляется следующим образом.

1. При каждом положении луча по азимуту и углу места сигнал в I-м стробе дальности подается на вход N доплеровских фильтров, в которых осуществляется селекция по частоте.

2. Амплитуда сигнала A(I,J) на выходе каждого J-го фильтра запоминается в матрице амплитуд А для I, J-го синтезированного пространственного элемента разрешения.

3. Последовательно в процессе формирования матрицы А относительно каждого I, J-го ДЭР, амплитуда которого A(I,J) превышает порог обнаружения (соответствует отражению от поверхности) строится пространственный строб в трехмерной прямоугольной системе координат x, y, z с i, j, k-ми элементами дискретизации, размеры которых на плоскости х, y меньше минимального диаметра проекции ДЭР.

4. Для каждого i, j, k-го элемента дискретизации в стробе проверяется принадлежность его координат x_i, y_j, z_k I, J-му ДЭР путем сопоставления сферических координат R, ϕ, θ элемента x_i, y_j, z_k с границами области D I, J-го ДЭР, установленными заранее в сферической самолетной системе координат с учетом вектора скорости движения объекта-носителя путем проверки выполнения системы неравенств

где R_I, ϕ_J, θ_J - известные сферические координаты центра I, J-го ДЭР, причем азимут ϕ_J соответствует J-му фильтру частот; Δϕ, Δθ, b - известные для каждого положения луча параметры аппроксимации ДЭР.

5. Если i, j, k-й элемент дискретизации с координатами центра x_i, y_j, z_k принадлежит области D, то амплитуда A(I,J) запоминается в матрице А, а координата z_k запоминаются в матрице Z. Если области D принадлежат несколько элементов дискретизации с одинаковыми координатами x_i, y_j и различными координатами z_k, то в матрице Z запоминается максимальное значение z_k.

6. Указанные операции повторяются для всех положений луча, тем самым формируются матрицы А и Z, которые представляют трехмерное изображение поверхности в зоне обзора РЛС.

7. Полученные матрицы А и Z привязываются к текущему дискретному моменту времени t_μ (μ=0, 1, 2, ...) и передаются на алгоритмы пространственно-временной обработки и вывода изображения на экран индикатора.

8. Если пространственно-временная обработка не осуществляется, то операции п.4 выполняются в сферической системе координат. В этом случае координатами центра i, j, k-го элемента дискретизации являются R_i, ϕ_j, θ_k - дальность, азимут, угол места и сопоставление R_i, ϕ_j, θ_k с границами ДЭР проводится без пересчета координат. На алгоритмы индикации выдаются матрицы: А - матрица амплитуд в координатах дальность - азимут и Θ - матрица третьей координаты (угла места).

Предлагаемый способ может применяться как на малой, так и большой высоте. В частном случае высотного полета матрицы Z или Θ не используются, так как высотой поверхности пренебрегают, и на индикацию выдается одна матрица двумерного (плоского) РЛИ А, традиционно получаемая в существующих системах доплеровского обужения.

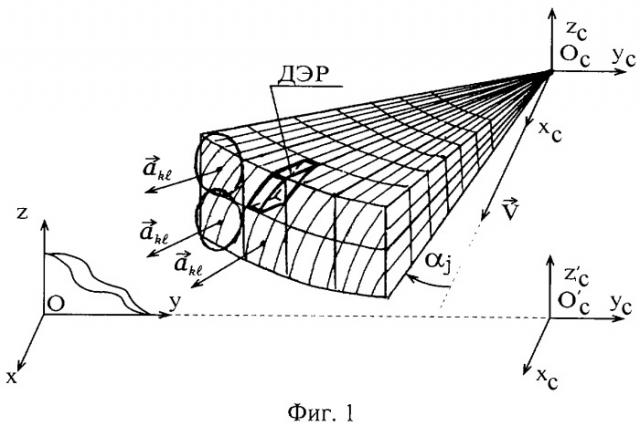
Расчет границ пространственных областей ДЭР сводится к следующему. В текущий момент времени t_μ объект-носитель РЛС рассматривается в самолетной системе координат <О_C, х_C, y_C, z_C>. Начало координат - точка О_C совпадает с центром масс самолета, ось О_Cx_C направлена вперед по строительной оси самолета, ось О_Cy_C лежит в плоскости левого крыла. Одновременно рассматривается сферическая система координат <О_c, R_c, ϕ_c, θ_c>, R - дальность, ϕ - азимут, θ - угол места, положительное направление отсчета ϕ и θ - против часовой стрелки относительно оси О_Cх_C, начало координат совпадает с точкой О_C. Ось симметрии антенны, совпадающая с вектором а на фиг.1 и фиг.2, занимает ряд фиксированных угловых положений по ϕ и θ (в горизонтальной и вертикальной плоскостях) с помощью электронного управления лучом, угловые координаты ДНА составляют ϕ±Δϕ/2 и θ±Δθ/2, где Δϕ и Δθ - размеры элементов разрешения (ЭР) по углам (ширина ДНА по азимуту и углу места). При данных ϕ и θ формируются ЭР по дальности R размера ΔR: R±ΔR/2.

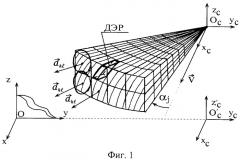
Элемент разрешения антенны (ЭР) представляет пространственную фигуру, образованную пересечением конической поверхности ДНА с вершиной в точке О_c, угловыми координатами (ϕ_о, θ_о) оси симметрии (вектора а на фиг.2) и двух сферических поверхностей постоянного уровня дальности с центром в точке О_с. Центром данного ЭР является точка О с сферическими координатами (R_o, ϕ_о, θ_o), положительный отсчет ϕ и θ осуществляется против часовой стрелки относительно оси О_сх_с.

Наличие доплеровских узкополосных фильтров с геометрической точки зрения означает дополнительное рассечение поверхности ЭР рядом конических поверхностей постоянного уровня скорости доплеровской частоты с вершиной в точке О_с и осью симметрии, совпадающей с вектором скорости ν движения объекта-носителя РЛС, направленного по оси О_сх_с. В результате образуются более мелкие элементы разрешения в виде сложных пространственных областей ДЭР (доплеровские элементы разрешения) разных размеров и с различной ориентацией в пространстве.

Положение конкретного ДЭР определяется углом α, который соответствует определенному номеру узкополосного доплеровского фильтра частот. Разрешение по углу α составляет величину Δα, которая связана нелинейной зависимостью с разрешением по частоте Δf. При фиксированной скорости ν движения и равномерном разбиении полосы частот (Δf=const) шкала α∈[0, π/2] разбивается на неравномерные промежутки α_n±Δα_n/2.

Задача состоит в определении сферических координат границ ДЭР, что необходимо для формирования матриц трехмерного РЛ-изображения поверхности.

Принципиальное решение задачи может быть получено следующим образом. Обозначим α_n - угол между осью О_сх_с (вектором ν) и образующей О_сО_n (вектором а_n) n-го конуса постоянного угла α_n - фиг.2.

Связь α_n с угловыми координатами (ϕ_n, θ_n) вектора а_n устанавливается по формуле

где cosα_n находится через скалярное произведение орта i_c оси О_сх_с и орта а_n оси О_сО_n. Действительно, координаты вектора а_n, имеющие в местной прямоугольной системе <O_n, х_n, y_n, z_n> n-го ДЭР канонический вид (1,0,0), в самолетной системе <О_с, х_с, y_c, z_c> находятся по формуле связи старых и новых координат при преобразовании типа поворота на угол ϕ_n вокруг оси О_сz_c и затем поворота на угол θ_n вокруг оси О_сy′_c:

что равносильно повороту i_c=(1,0,0) на угол ϕ_n вокруг оси O_cz_c в плоскости О_с, х_с, y_с и затем повороту на угол θ_n вокруг оси О_су′_с в плоскости O_cx′_cz_c. В результате получается вектор

причем |а_n|=1. Тогда cosα_n=i_c·a_n=cosϕ_n·cosθ_n.

Использование формулы (1) при определении координат n-го ДЭР данного ЭР сводится к численному решению нелинейного уравнения для каждого значения доплеровского угла α∈[α_n-Δα_n/2, α_n+Δα_n/2], где α_n - доплеровский угол, соответствующий доплеровской частоте f_n и центру n-го ДЭР, при ограничениях

Смещение (приращение) частоты Δf_n за счет смещения (приращения) угла отклонения Δα_n находится по формуле (при условии, что Δα_n мало):

где ν - путевая скорость (объекта-носителя РЛС), λ - длина волны излучения (например, Кондратенков Г.С, Фролов А.Ю. Радиовидение. Радиолокационные системы дистанционного зондирования Земли. Учебное пособие для вузов / Под ред. Г.С. Кондратенкова. - М.: Радиотехника, 2005, с.38).

Для работы в реальном масштабе времени требуется более простое описание ДЭР в виде линейных зависимостей. В работе (Клочко В.К. Методика определения координат доплеровских элементов разрешения бортовой радиолокационной системы при получении трехмерных изображений поверхности // Автометрия, 2002, №6. - С.12-20) предлагается методика определения таких зависимостей, основанная на аппроксимации конических и сферических поверхностей цилиндрическими и плоскими, допустимая в пределах ЭР. При этом получается линейная модель ДЭР и следующий алгоритм определения координат границ доплеровского элемента разрешения.

1. Для каждого положения луча РЛС с шириной по азимуту и углу места Δϕ, Δθ определяется доплеровский угол α, соответствующий центру ЭР.

2. Находится диапазон [α_min, α_max] значений доплеровского угла α, соответствующий данному ЭР, где в случае круговой (точечной) ДНА α_min=α-Δϕ/2, α_max=α+Δϕ/2, и устанавливается соответствие

с полосой доплеровских частот так, что каждому J-му угловому промежутку [α_J, α_J+1]⊂[α_min, α_max] доплеровского элемента разрешения D соответствует полоса частот [f_J, f_J+1]⊂[f_min, f_max] доплеровского фильтра.

3. Для каждого J-го ДЭР определяются параметры аппроксимации (ϕ_J, Δϕ_J, θ_J, Δθ_J, b_J) и задается линейное описание относительно его углового центра (ϕ_J, θ_J):

Расчеты не зависят от дальности R и выполняются заранее для различных значений (ϕ_J,θ_J), которые определяются режимом наблюдения РЛС.

4. На множестве I-х элементов разрешения дальности ДЭР принимает окончательный вид

5. Если принять упрощение (удобное, например, для веерной ДНА), что параметры аппроксимации не зависят от J в пределах данного направления: (ϕ_J, Δϕ, θ_J, Δθ, b), то описание (4) принимает вид

где R_I, ϕ_J, θ_J - известные сферические координаты центра I, J-го ДЭР, причем азимут ϕ_J связан с углом места θ_J зависимостью cosα_J=cosϕ_J·cosθ_J, доплеровский угол α_J соответствует частоте f_J J-го фильтра частот: ν - путевая скорость, λ - длина волны излучения, ΔR - разрешение по дальности, Δϕ, Δθ, b - известные для каждого положения луча параметры аппроксимации границ ДЭР по углам.

Пересчет ДЭР в прямоугольную систему координат осуществляется следующим образом.

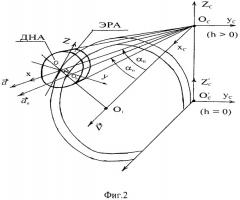
1. Задается прямоугольная сетка i, j, k координат в системе <O′_С, x_С, y_С, z_С> на плоскости нулевого уровня высоты (фиг.3) с элементами дискретизации Δх, Δy, Δz, причем размеры Δх и Δy выбираются меньше минимального диаметра проекции ДЭР на плоскость х_с, y_с.

2. Для каждого ДЭР в соответствии с формулами связи прямоугольных и сферических координат х=R·cosθ·cosϕ, y=R·cosθ·sinϕ, z=R·sinθ+h, где h - высота в точке О_с, устанавливаются диапазоны возможных значений по х, у, z в окрестности данного ДЭР (в прямоугольном стробе - фиг.3) и осуществляется перебор точек (узлов) прямоугольной сетки в указанных диапазонах. Для каждой такой i, j, k-й точки с координатами х=x_i, y=y_j, z=z_k (нумерация i, j, k соответствует прямоугольной системе) вычисляются соответствующие им сферические координаты в самолетной системе:

Координаты R, ϕ, θ проверяются на принадлежность данному ДЭР путем проверки выполнения системы неравенств (4) или (5).

Если i, j, k-я точка удовлетворяет системе (4) или (5), то в матрице А с элементами A(i,j) запоминается амплитуда данного ДЭР, а в матрице Z с элементами Z(i,j) запоминается наибольшее значение третьей координаты (высоты) относительно нулевого уровня. Таким образом, данный ДЭР описывается семейством прямоугольных ячеек {(i,j)} на плоскости с характеристиками A(i,j), Z(i,j), ∀i,j ∈ ДЭР.

Полученные матрицы трехмерного изображения поверхности A, Z в прямоугольной системе координат, привязанные к текущему дискретному моменту времени t_μ, μ=0, 1, 2, ..., передаются на алгоритмы пространственно-временной обработки изображений, предназначенные для повышения качества изображения (устранение смазываний, подавление спекл-шумов: Клочко В.К. Пространственно-временная обработка информации бортовой РЛС при получении трехмерных изображений поверхности // Радиотехника, 2004, №6. - С.3-11) и алгоритмы вывода изображений на экран.

Если алгоритмы пространственно-временной обработки не используются, то отпадает необходимость пересчета в прямоугольную систему координат и алгоритм формирования трехмерного изображения сводится к следующему.

1. Задается сетка i, j, k сферических координат в самолетной системе <О_с, R_c, ϕ_с, θ_с> с элементами дискретизации δR, δϕ, δθ, причем размеры δR и δϕ выбираются меньше минимальной проекции ДЭР на плоскость R_c, ϕ_c.

2. Для каждого ДЭР устанавливаются диапазоны возможных значений по R, ϕ, θ в окрестности данного ДЭР и осуществляется перебор точек (узлов) сферической сетки в указанных диапазонах. Для каждой такой i, j, k-й точки с координатами R_i, ϕ_j, θ_k проверяются ее принадлежность данному ДЭР путем проверки выполнения системы неравенств (4) или (5).

Если i, j, k-й узел удовлетворяет системе (4) или (5), то в матрице А запоминается амплитуда данного ДЭР, а в матрице Θ запоминается наибольшее значение третьей координаты (азимута), и данный ДЭР описывается семейством точек (пикселов) {(i, j)} на плоскости с характеристиками A(i,j), Θ(i,j), ∀i,j ∈ ДЭР.

Предложенный способ получения трехмерных изображений использует доплеровскую информацию для повышения разрешения не только по азимуту ϕ, но и по углу места θ, что позволяет более точно изображать поверхность, а также повышать в несколько раз точность определения ее высоты (при определенном взаимном положении векторов ν и а). Возможность наблюдать изображение поверхности (и объектов на поверхности) с дополнительной информацией о высоте (например, в градациях цветности или в изометрии) повышает безопасность маловысотных полетов и дает возможность более точно определять положение объектов на поверхности в условиях отсутствия оптической видимости.

Способ получения трехмерного изображения поверхности в зоне обзора бортовой РЛС маловысотного полета, заключающийся в создании режима построчного обзора контролируемого участка пространства в сочетании с узкополосной доплеровской фильтрацией принятых сигналов, позволяющей рассечь пространственные элементы разрешения антенны на мелкие части (доплеровские элементы разрешения - ДЭР), и формировании матрицы трехмерного изображения поверхности в виде совокупности амплитуд отраженных сигналов, зафиксированных в ДЭР, при этом за счет быстрого электронного переключения луча РЛС смещают луч по азимуту и углу места построчно на ширину диаграммы направленности антенны в зоне обзора и при каждом положении луча по азимуту и углу места измеряют амплитуду сигнала на выходе J-го фильтра доплеровских частот в I-м элементе разрешения дальности, тем самым получают двумерное изображение поверхности в пределах зоны обзора при каждом положении луча РЛС в виде совокупности амплитуд, отличающийся тем, что для каждой измеренной амплитуды, превышающей порог обнаружения (соответствующей отражению от поверхности), выбирают i, j, k-e элементы дискретизации прямоугольной сетки х_i, y_j, z_k, сферические координаты которых R, ϕ, θ принадлежат области ДЭР, путем проверки системы неравенств:

где R_I, ϕ_J, θ_J - известные сферические координаты центра ДЭР, R_I - дальность, ϕ_J - азимут, θ_J - угол места, ΔR - разрешение по дальности, Δϕ, Δθ, b - известные для каждого положения луча параметры аппроксимации границ ДЭР по углам, и если i, j, k-e элементы дискретизации принадлежат области ДЭР, то запоминают амплитуду данного ДЭР в матрице амплитуд А, а максимальное значение третьей координаты высоты - в матрице Z, затем повторяют эти операции для всех положений луча и тем самым формируют трехмерное изображение поверхности в зоне обзора РЛС в виде двумерных матриц А и Z.