Способ измерения высоты объектов на поверхности при получении трехмерного радиолокационного изображения поверхности с объектами на базе бортовой рлс маловысотного полета

Способ измерения высоты объектов на поверхности при получении трехмерного радиолокационного изображения поверхности с объектами на базе бортовой рлс маловысотного полета

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, а именно к радиолокационным системам наблюдения за поверхностью на базе бортовой РЛС маловысотного полета, работающей в режиме высокого разрешения по азимуту (например, доплеровского обужения диаграммы направленности антенны - ДНА).

В данном режиме наблюдения образуется плоское радиолокационное изображение (РЛИ) поверхности в координатах дальность - азимут (или дальность - доплеровская частота при доплеровском обужении) с разрешением, позволяющим наблюдать объекты на поверхности (Радиолокационные станции с цифровым синтезированием апертуры антенны. / А.Н.Антипов, В.Т.Горяинов, А.Н.Кулин и др. Под ред. В.Т.Горяинова. М.: Радио и связь, 1988. 304 с.). Однако при таком способе получения РЛИ высота объектов на поверхности не определяется, что затрудняет идентификацию изображений объектов при их распознавании. В связи с этим возникает необходимость получения трехмерных изображений поверхности с объектами, на которых отображается высота объектов.

Наиболее близким по технической сущности является способ получения двумерного (плоского) РЛИ поверхности в режиме узкополосной доплеровской фильтрации (Кондратенков Г.С., Фролов А.Ю. Радиовидение в передней зоне обзора бортовой радиолокационной станции с синтезированной апертурой антенны. / Радиотехника, 2004, №1. С.47-49).

В соответствии с данным способом формируется матрица A(I,J) плоского РЛИ, элементы которой представляют амплитуды сигналов отражения, измеренные в системе координат I-х элементов разрешения дальности и J-x элементов разрешения по азимуту. Недостатком данного способа является то, что при формировании РЛИ высота объектов на поверхности не определяется.

Технический результат направлен на определение высоты объектов на поверхности путем измерения угла места θ(I,J) совместно с амплитудой A(I,J) элемента поверхности в каждом I, J-м элементе разрешения и получение трехмерного РЛИ поверхности с объектами в виде совокупности матриц высот H(i,j) и амплитуд A(i,j) в i, j-x элементах дискретизации прямоугольной сетки координат.

Технический результат предлагаемого технического решения достигается тем, что способ измерения высоты объектов на поверхности при получении трехмерного радиолокационного изображения поверхности с объектами на базе бортовой РЛС маловысотного полета заключается в формировании матрицы амплитуд отраженного сигнала A(I,J) в I-х элементах разрешения дальности и J-x элементах разрешения по азимуту, отличается тем, что путем электронного переключения осуществляют последовательное смещение луча РЛС по углу места против часовой стрелки на часть ширины диаграммы направленности антенны (ДНА) при фиксированном азимутальном положении и при каждом k-м положении луча по углу места измеряют амплитуды отраженного сигнала u(k) в I, J-x элементах разрешения по дальности и азимуту, далее для последовательности полученных измерений u(1), u(2),..., u(k),... в каждом I, J-м элементе разрешения дальности и азимута вычисляют оценки амплитуд в синтезированных элементах разрешения по углу места путем умножения измерений на весовые коэффициенты и суммирования результатов умножений по формуле:

где h(l) - весовой коэффициент,

l - номер весового коэффициента, целое число,

k - номер синтезированного элемента разрешения по углу места,

n - нечетное число,

определяют k_μ-e положение луча антенны, соответствующее минимальному значению угла места, и сам угол места θ_μ, отсчитываемый от горизонтальной плоскости, соответствующий элементу поверхности, при котором оценка амплитуды превышает порог обнаружения сигнала отражения от поверхности, затем предельное k_μ-e значение оценки амплитуды и соответствующее k_μ-e значение угла места θ_μ запоминают в матрице амплитуд А: и матрице третьих координат Θ: Θ(I,J)=θ_μ, которые пересчитывают в прямоугольную систему координат в виде матрицы амплитуд A(i,j) и матрицы высот H(i,j) в i, j-x элементах дискретизации прямоугольной сетки, причем в процессе пересчета запоминают только максимальную высоту, вычисляемую по формуле

где R_I - расстояние по наклонной дальности между РЛС, расположенной на высоте h, и данным I, J-м элементом разрешения по дальности и азимуту.

Способ осуществляется следующим образом.

1. В режиме высокого разрешения по азимуту для первого положения луча РЛС по углу места θ₁, измеряемого от горизонтальной плоскости движения объекта-носителя РЛС, формируют матрицу амплитудного изображения поверхности U₁(I,J), где I - номер элемента разрешения по дальности R_I, J - номер синтезированного элемента разрешения по азимуту ϕ_J.

2. Путем электронного переключения луча РЛС смещают луч по углу места на n-ю часть ширины ДНА в положение θ₂ в направлении против часовой стрелки от нижнего положения обзора поверхности и в режиме высокого разрешения по азимуту формируют вторую матрицу изображения U₂(I,J) в тех же I, J-x элементах разрешения.

3. Таким образом путем последовательного поворота луча РЛС против часовой стрелки по углу места на n-ю часть ширины ДНА в положения θ₁, θ₂,..., θ_k,... получают последовательность матриц U₁(I,J), U₂(I,J),..., U_k(I,J),... в системе I, J-x элементов разрешения.

4. Для каждого I, J-го элемента разрешения по дальности и азимуту рассматривают последовательность измеренных амплитуд u(1)=U₁(I,J), u(2)=U₂(I,J),..., u(k)=U_k(I,J),... сигналов отражения, полученных при различных k-x положениях луча РЛС по углу места (k=1, 2,...).

5. Последовательность измерений u(k-n/2),..., u(k),..., u(k+n/2), где n - нечетное число измерений, необходимых для получения оценки в k-м синтезированном элементе разрешения (n≥m, m - нечетное число элементов дискретизации по ширине ДНА на уровне 0,5 мощности) умножают на весовые коэффициенты h(l), h(-n/2),..., h(0),..., h(n/2), расчет которых осуществляют заранее по методике, изложенной ниже, а результаты умножений суммируют.

6. В результате по формуле

где h(l) - весовой коэффициент, l - номер весового коэффициента, целое число, k - номер синтезированного элемента разрешения по углу места, находят оценки , представляющие амплитуды сигнала отражения в k-x синтезированных элементах разрешения по углу места (с повышенным разрешением).

7. Определяют предельное положение k_μ, соответствующее минимальному значению угла места θ_μ линии визирования антенны (или максимальной высоте поверхности или объекта на поверхности - отсчет θ ведется от горизонтальной плоскости положения объекта-носителя РЛС), при котором амплитуда еще превышает порог обнаружения сигнала отражения от поверхности или объекта на поверхности. Значение угла места θ_μ для I, J, k_μ-го элемента поверхности запоминают в координатах I, J в матрице Θ: Θ(I,J)=θ_μ, a амплитуду этого же элемента запоминают в матрице A: . Таким образом, на множестве значений I, J формируют матрицы углов места (третьих координат) Θ(I,J) и амплитуд A(I,J) элементов поверхности в координатах I, J-x элементов разрешения дальности и азимута.

8. Для удобного визуального восприятия матрицы A(I,J) и Θ(I,J) пересчитывают в прямоугольную систему координат x_i, y_j с i, j-ми элементами дискретизации, размеры которых меньше линейных размеров элементов разрешения (формулы пересчета даны ниже), и представляют в виде матрицы амплитуд A(i,j) и матрицы высот H(i,j) (нумерация i, j отличается от нумерации I, J), причем в i, j-м элементе дискретизации из нескольких возможных значений запоминают только максимальную высоту и соответствующую ей амплитуду.

Высоту вычисляют по формуле

где R_I - расстояние по наклонной дальности между РЛС, расположенной на высоте h, и данным I, J-м элементом разрешения по дальности и азимуту.

9. Полученные таким образом матрица высот H(i,j) и матрица амплитуд A(i,j) представляют трехмерное РЛИ поверхности, которое далее передают на алгоритмы индикации для отображения на экране пилота, а также на алгоритмы вторичной обработки РЛИ.

10. Вместо операций п.п.5-7 определения Θ(I,J)=θ_μ путем повышения разрешающей способности РЛС по углу места θ может быть использован более простой способ измерения предельного значения θ_μ, который заключается в определении такого положения k_μ луча РЛС по углу места при его последовательном смещении на n-ю часть ширины ДНА, при котором сигнал отражения от поверхности в I, J-м элементе разрешения исчезает (луч выходит за пределы поверхности в I, J-м элементе разрешения). При этом угол места θ_μ определяют по нижней границе ДНА. Соответствующую θ_μ оценку амплитуды находят по формуле

где α_n - коэффициент усиления антенны в n-й части ДНА. Однако отношение сигнал/шум на периферии ДНА значительно меньше, чем в ее центральной части и оценка (2) в большей степени подвержена влиянию помех, чем оценка (1).

Пересчет матриц A(I,J) и Θ(I,J) в прямоугольную систему координат осуществляется следующим образом.

Рассматривается пространственный элемент разрешения поверхности, синтезированный по θ:

где θ_K=Θ(I,J), R_I, ϕ_J, θ_K - центр I, J, K-го элемента разрешения, ΔR, Δϕ, Δθ - его размеры.

Задается прямоугольная сетка i, j, k в самолетной системе координат <O'_C,x_C,y_C,z_C> на плоскости нулевого уровня высоты h (O'_C - проекция точки O_C (0,0,h) положения РЛС на плоскость h=0) с элементами дискретизации Δx, Δy, Δz, причем размеры Δx и Δу выбираются меньше минимального диаметра проекции V на плоскость хс, yc.

Для каждой области V в соответствии с формулами связи прямоугольных и сферических координат

х=R·cosθ·cosϕ, y=R·cosθ·sinϕ, z=R·sinθ+h,

где h - высота в точке Oc, устанавливаются диапазоны возможных значений по х, y, z в окрестности V и осуществляется перебор точек (узлов) прямоугольной сетки в указанных диапазонах. Для каждой такой i, j, k-й точки с координатами х=xi, y=yj, z=zk (нумерация i, j, k соответствует прямоугольной системе) вычисляются соответствующие им сферические координаты в самолетной системе:

Координаты R, ϕ, θ проверяются на принадлежность V путем проверки выполнения системы неравенств ,

.

Если i, j, k-я точка удовлетворяет данной системе, то в матрице A(i,j) запоминается амплитуда A(I,J), зафиксированная в пространственной области V, а в матрице H(i,j) запоминается наибольшее значение третьей координаты z_k (высоты) относительно нулевого уровня. Таким образом, данная пространственная область V описывается семейством прямоугольных ячеек {(i,j)} на плоскости с характеристиками A(i,j), Н(i,j), ∀i,j∈V.

Расчет весовых коэффициентов сводится к следующему. При k-м положении луча РЛС по углу места амплитуда сигнала u(k) на выходе суммарного измерительного канала РЛС при фиксированных I, J-x элементах разрешения по дальности и азимуту после некоторых преобразований подчинена линейной модели

где α(l) - коэффициенты ДНА; x(k) - амплитуда сигнала поля отражения в k-м элементе дискретизации по углу места, подлежащая восстановлению (оцениванию) по результатам интегральных (суммарных) наблюдений u(k); p(k) - случайная центрированная помеха с дисперсией . Модель (3) можно записать, изменив нумерацию, в виде

Тогда для первых n измерений (нечетное число n≥m) выражение (4) представляет систему n уравнений с n+m-1 неизвестными и n помехами:

или в матричной форме:

Для моделей (3)-(6) разработаны различные алгоритмы нахождения оценок искомых амплитуд поля отражения Х по критерию минимума среднего квадрата ошибки оценивания или минимума квадрата нормы с учетом корреляционных свойств полей x(k) и u(k). Такие алгоритмы линейны относительно измерений y(k) и имеют или конечную память:

или рекуррентную структуру (например, Клочко В.К., Чураков Е.П., Фатьянов С.О. Калмановский алгоритм восстановления смазанного радиолокационного изображения. // Известия вузов. Радиоэлектроника. 2004. Том 47. №9-10. С.54-59):

где h(k) и H(k) - соответственно весовые коэффициенты и матрица весовых коэффициентов; а^T=(α₁,α₂,...,α_m); В - вспомогательная матрица; Т - символ транспонирования.

Алгоритмы (7), (8), как алгоритмы статистического оценивания по ограниченному числу измерений (число n измерений в (5) меньше числа n+m-1 оцениваемых параметров), обладают сглаживающими свойствами и их точность при оценивании резко меняющихся амплитуд x(k) ограничена.

Для повышения точности оценивания в работе (Клочко В.К. Повышение разрешающей способности РЛС по данным суммарного и разностного каналов. // Вестник РГРТА. 2004, вып.15. С 56-60) предлагается дополнительно использовать данные второго (разностного) канала РЛС. При этом число изменений (размерность вектора U) удваивается и превышает число оцениваемых параметров (2n>n+m-1, n≥m), что позволяет находить оценки искомых параметров Х методом максимального правдоподобия решения системы 2n уравнений типа (5) с n+m-1 неизвестными. В матричной форме минимизация функции по приводит к оценкам регуляризованного метода наименьших квадратов (РМНК):

где δ - параметр регуляризации, необходимый для обращения плохо обусловленной матрицы А^TА; Е - единичная матрица; Н=(А^TА)^-1А^T - матрица весовых коэффициентов. При обращении A^TА удобно использовать рекуррентную процедуру:

где а_i - i-я строка матрицы А коэффициентов ДНА.

При наблюдении за контрастными объектами предусматривается дополнительная обработка восстановленного изображения типа кусочно-постоянной аппроксимации с рекуррентным определением параметров аппроксимации.

Оценка представляет амплитуду сигнала отражения в m-й части ДНА (элементе дискретизации) по углу места, соответствующей центру k-го положения луча РЛС (синтезированного элемента разрешения по углу места). При вычислении используется центральная строка матрицы Н, соответствующая минимуму дисперсии ошибки оценивания ковариационной матрицы . Алгоритм оценивания (9) представляет линейную комбинацию измерений, взятых с заранее просчитанными весовыми коэффициентами. Как показывает моделирование, РМНК-оценки (9) могут быть использованы и для модели измерений (3) одного суммарного канала РЛС, при этом алгоритм оценивания имеет вид (7), где весовые коэффициенты h(l) находятся по методике (9) для вектора U размерности n.

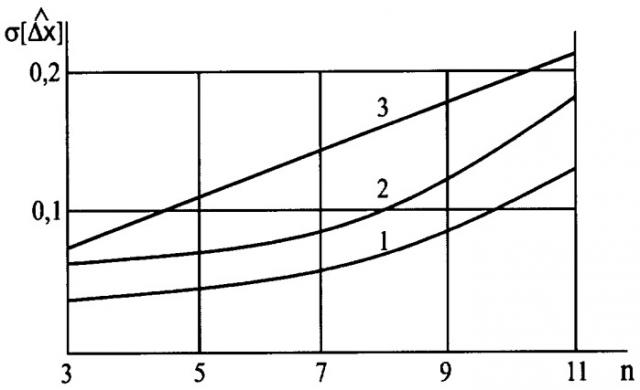
На чертеже представлены результаты моделирования работы алгоритма РНМК (9), (10) при n=m в сравнении с рекуррентным алгоритмом (8) в виде зависимостей среднеквадратического отклонения (СКО) ошибки оценивания от ширины n ДНА. Моделировались измерения (3) при наблюдении двух протяженных контрастных объектов прямоугольной формы в одном элементе дальности и азимута. Амплитуды сигналов отражения составляли 1 и 2 при СКО помехи σ_P=0,1. Параметр регуляризации выбирался равным δ=0,1. Зависимость 1 соответствует РМНК для двух каналов измерения, зависимость 2 - РМНК для одного канала измерения, зависимость 3 - рекуррентный алгоритм для одного канала. Точность σ[Δx] восстановления х(k) по данным двух каналов соизмерима с уровнем помех σ_p=0,1 для n=3, 5, 7, 9 при наличии операций (11) и для n=3, 5, 7 при отсутствии этих операций (зависимости смещаются вверх на 0,05 по оси ординат). При увеличении ширины ДНА n точность восстановления ухудшается. Можно принять, что синтезированный элемент разрешения по углу места составляет 1/7-1/9 часть ширины ДНА для двух каналов и 1/5-1/7 часть ширины ДНА для одного канала, соответственно точность измерения высоты по результатам моделирования для двух каналов составляет 1/7-1/9 ширины ДНА в линейных единицах (с учетом наклонной дальности).

Предложенный способ измерения высоты при получении трехмерного РЛИ поверхности позволяет совместно с амплитудным изображением A(i,j) выводить на экран индикатора матрицу высот H(i,j) с указанием высоты либо в градациях основных цветов (соответственно уровню высоты), либо в изометрии. Это дает возможность пилоту своевременно обнаруживать препятствия при маловысотном полете, что увеличивает безопасность таких полетов, а также правильно идентифицировать изображения объектов на поверхности, что увеличивает вероятность правильного обнаружения и распознавания РЛИ объектов.

Способ измерения высоты объектов на поверхности при получении трехмерного радиолокационного изображения поверхности с объектами на базе бортовой РЛС маловысотного полета, заключающийся в формировании матрицы амплитуд отраженного сигнала A(I,J) в I-х элементах разрешения дальности и J-x элементах разрешения по азимуту, отличающийся тем, что путем электронного переключения осуществляют последовательное смещение луча РЛС по углу места против часовой стрелки на часть ширины диаграммы направленности антенны (ДНА) при фиксированном азимутальном положении и при каждом k-м положении луча по углу места измеряют амплитуды отраженного сигнала u(k) в I, J-x элементах разрешения по дальности и азимуту, далее для последовательности полученных измерений u(1), u(2), ..., u(k), ... в каждом I, J-ом элементе разрешения дальности и азимута вычисляют оценки амплитуд в синтезированных элементах разрешения по углу места путем умножения измерений на весовые коэффициенты и суммирования результатов умножений по формуле:

где h(l) - весовой коэффициент;

l - номер весового коэффициента, целое число;

к - номер синтезированного элемента разрешения по углу места;

n - нечетное число,

определяют k_μ-е положение луча антенны, соответствующее минимальному значению угла места, и сам угол места θ_μ, отсчитываемый от горизонтальной плоскости, соответствующий элементу поверхности, при котором оценка амплитуды превышает порог обнаружения сигнала отражения от поверхности, затем предельное k_μ-е значение оценки амплитуды и соответствующее k_μ-е значение угла места θ_μ запоминают в матрице амплитуд А: и матрице третьих координат θ: θ(I,J)=θ_μ, которые пересчитывают в прямоугольную систему координат в виде матрицы амплитуд A(i,j) и матрицы высот H(i,j) в i, j-x элементах дискретизации прямоугольной сетки, причем в процессе пересчета запоминают только максимальную высоту, вычисляемую по формуле:

где R_I - расстояние по наклонной дальности между РЛС, расположенной на высоте h, и данным I, J-м элементом разрешения по дальности и азимуту.