Аутентификация в защищенной компьютеризованной игровой системе

Аутентификация в защищенной компьютеризованной игровой системе

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение относится к компьютеризованным игровым системам для игры на ставки, более конкретно к использованию методов аутентификации с использованием доказательств с нулевым знанием (zero knowledge proof - ZKP) в качестве базы для обеспечения защиты в компьютеризованной игровой системе для игры на ставки.

Предшествующий уровень техники

Азартные игры являются излюбленными играми людей уже в течение тысяч лет и в последнее время становятся все более распространенными и популярными. Как и в случае других форм развлечения, игроки с удовольствием играют в самые разнообразные и новые виды игр. Новые игры доставляют дополнительное удовольствие от игры. Как хорошо известно в технике и используется в настоящем описании, термины «игра» и «игровые устройства» используются для указания на то, что с этим связана некоторая форма пари, осуществление ставок, и что игроки должны делать ставки на стоимость, будь то реальные деньги или некоторый эквивалент стоимости, например жетон или кредит.

Популярной азартной игрой является автомат для игры в слоты. Обычно автомат для игры в слоты обеспечивает игроку возможность осуществления ставки на некоторую стоимость, например сумму денег, жетонов игорного дома, установленного кредита или другое представление денег или кредита. После того как ставка сделана, игрок приводит в действие игровой автомат, чтобы вызвать возникновение случайного события. Игрок ставит ставку на то, что это конкретное событие произойдет и обеспечит возвращение стоимости игроку. В стандартном устройстве имеется множество барабанов, которые вращаются и в конечном счете останавливаются, отображая случайную комбинацию некоторой формы знаков, например чисел или символов. Если это отображение содержит одно из предварительно выбранного множества выигрышных комбинаций, то автомат выдает деньги в лоток выплат или увеличивает показание счетчика кредита на величину выигрыша игрока. Например, если игрок первоначально поставил две монеты конкретного номинала, и этот игрок получил выплату, то игрок может получить то же число или кратное число от суммы ставки в монетах того же достоинства, в каких была сделана ставка.

Имеется множество различных форматов для генерации изображения случайных событий, которые могут произойти, для определения выплат в устройствах для игры на ставки. Стандартным или первоначальным форматом было использование трех барабанов с символами, распределенными по поверхности барабана. Когда три барабана приводились во вращение, они в конечном счете прекращали вращаться и показывали комбинацию из трех символов (например, при использовании трех барабанов и единственной линии выплаты в качестве ряда в середине области, где визуализируются символы). Путем соответствующего распределения и варьирования символов на каждом из барабанов случайное возникновение предварительно определенных выигрышных комбинаций может быть обеспечено с математически предварительно определенными вероятностями. Путем четкого обеспечения конкретных вероятностей для каждого из предварительно выбранных выигрышных результатов можно легко контролировать точные шансы, которые будут определять сумму выплат для каждой конкретной комбинации и долю выплат по ставкам для игорного дома.

Количество разных форматов игровых автоматов, которые были разработаны в процессе развития от простого игрового автомата для игры в слоты с тремя барабанами, выросло в огромных масштабах с разработками игровых автоматов для видеоигр. Вместо наличия только механических элементов, таких как колеса или барабаны, которые вращались и останавливались для отображения случайным образом символов, игровые автоматы для видеоигр и быстро возрастающая сложность аппаратного и программного обеспечения привели к бурному развитию новых весьма привлекательных игровых автоматов. Первые игровые автоматы для видеоигр просто имитировали или моделировали игру с механическими барабанами, поскольку существовало мнение, что игроки желали бы играть только в те же самые игры. Поэтому первые видеоигры представляли собой имитированные игровые автоматы для игры в слоты. Использование игровых автоматов для видеоигр, предназначенных для новых игр, таких как покер и кено, пробили путь к осмыслению того, что имелось множество неиспользованных форматов для игровых автоматов. В настоящее время казино могут иметь сотни различных типов игровых автоматов со сравнимым количеством существенных различий в игре. Автомат может модифицироваться от традиционных автоматов с тремя барабанами с единственной линией выплат, видеоимитации игровых автоматов с тремя барабанами к имитированным автоматам для игры в слоты с пятью барабанами, с пятью столбцами, с выбором двенадцати и более отдельных линий выплат, включая расположенные случайным образом линии выплат, выплаты вразброс или выплаты для одного отображения. В дополнение к варьированию форматов для игр с большим успехом были введены призовые игры, призовые вознаграждения и прогрессивные джекпоты. Призовые игры могут быть связаны с осуществлением игры, которая совершенно отличается от первоначальной игры, например отображение видеоизображения скачек со ставками на отдельных лошадей, случайным образом сопоставляемых с игроками, которые получили право на призовую игру, вращение случайным образом барабана с фиксированными суммами призовых выплат для барабана (или его имитации), или попытка выбрать случайную карту, которая имеет более высокий номинал, чем карта, показанная от лица виртуального дилера.

Примеры таких игровых автоматов с отличающейся функцией призовой игры раскрыты в патентах США 5823874, 5848932, 5853041, в патентах Великобритании 2201821А, 2202984А, 2072395А и в патенте Германии 4014477А1. Каждый из этих патентов отличается способами игры в рамках призового раунда. Патент Великобритании 2201821А и патент Германии 3700861А1 описывают игровой автомат, в котором, после того как в первый раз достигнут выигрыш в игровом сегменте того типа, в котором используются барабаны, начинается второй сегмент, чтобы определить присужденное количество денег или дополнительных игр. Игра второго сегмента связана с использованием вращающегося барабана с приведенными на нем призовыми (например, количество монет или количество дополнительных игр) и вращающейся стрелки, которая будет указывать на сегменты на барабане со значениями призовых на нем. Игрок будет нажимать кнопку останова, и стрелка будет указывать на одно из значений. В описании указывается, что имеется определенный уровень способностей у игрока, связанный с остановкой барабана и стрелки (стрелок), а также что связанный компьютер действует для обеспечения случайного выбора циклически изменяющихся чисел для определения результатов в дополнительной выигрышной игре, что указывает на некоторый выбор случайным образом во втором игровом сегменте. Патенты США 5823874 и 5848932 описывают игровое устройство, содержащее первый стандартный игровой блок для отображения случайно выбранной комбинации знаков, причем отображаемые знаки выбраны из группы, состоящей из барабанов, знаков на барабанах, знаков игральных карт и их комбинаций; средство для генерации, по меньшей мере, одного сигнала, соответствующего, по меньшей мере, одному выбранному изображению знаков, первым игровым блоком; средство для обеспечения, по меньшей мере, одного различимого знака механического указателя призовой игры, причем упомянутый различимый знак указывает, по меньшей мере, на одну из множества возможных призовых игр, причем упомянутое средство для обеспечения оперативно связано с первым стандартным игровым блоком и активизируется в ответ на упомянутый сигнал. Реально второе игровое событие имитирует механический указатель призовой игры, такой как колесо рулетки или колесо с указательным элементом.

Видеотерминал представляет собой другую форму игрового устройства. Видеотерминалы работают тем же способом, что и обычные слот-автоматы или видеоавтоматы, за исключением того, что выдается квитанция о погашении вместо непосредственной выдачи выплаты.

Огромный массив игровых автоматов для электронных видеоигр, коммерчески доступных в настоящее время, не стандартизованы в промышленности или необходимым образом даже в рамках коммерческой линии устройств, выпускаемых одним изготовителем. Одной из причин такого отсутствия однородности или стандартизации является то обстоятельство, что операционные системы, которые используются в настоящее время в промышленности, являются примитивными. В результате программист должен часто создавать код для каждой отдельной функции, выполняемой индивидуальным автоматом. До настоящего времени, до правообладателя настоящего изобретения, не было известно ни одного изготовителя, который бы смог успешно создать универсальную операционную систему для преобразования существующего оборудования (которое включает в себя такие признаки, как повторно используемые модули кода), по меньшей мере частично, из-за ограничений в применимости и совместимости с существующими используемыми операционными системами. При создании новых игр по вышеназванным причинам в типовом случае создаются новые аппаратные средства и программное обеспечение.

Была сделана, по меньшей мере, одна попытка создать универсальную игровую машину (процессор), выделяющую код, ассоциированный с генерацией случайных чисел (RNG), и алгоритмы, применяемые к последовательности случайных чисел, из остатка кода. В патенте США 5707286 описано такое устройство. Патентовладелец понял, что модульный код обеспечит выгоды от использования, однако предложил выполнить модульными только RNG и алгоритмы передачи.

Отсутствие стандартной операционной системы способствовало поддержанию искусственно высокой цены на эти системы на рынке. Этому способствует использование уникальных и нестандартизованных интерфейсов аппаратных средств в различных выпускаемых видеоигровых системах. Различные аппаратные средства, различные коды доступа, различные связи выводов, различные жгуты проводки для соединения выводов, различные функции, обеспечиваемые с различных выводов, и другие разнообразные и различающиеся конфигурации в пределах систем препятствуют стандартизации в данной области техники. Это является предпочтительным для изготовителей игровых автоматов, поскольку игры для каждой системы предоставляются исключительным образом одним изготовителем, и системы в целом легко устаревают, так что рынок вынужден приобретать комплектный блок, а не просто заменять программное обеспечение и аппаратные средства. Таким образом, конкуренты не могут просто обеспечить одну игру, в которую можно было бы играть с использованием различных аппаратных средств. Решение этой проблемы представлено в совместно поданной настоящим заявителем заявке на «Видеоигровое устройство для игры на ставки с использованием универсального компьютеризованного контроллера и интерфейса ввода/вывода для уникальной архитектуры» № 09/405,921 от 24 сентября 1999, раскрытие которой включено в настоящее описание посредством ссылки.

Изобретение компьютеризованных игровых систем, которые включают в себя обычный или универсальный контроллер видеоигры на ставки, который может быть установлен в широком классе устройств для видеоигр без существенной модификации контроллера игры, сделало возможным стандартизацию многих компонентов и соответствующего программного обеспечения игр в игровых системах. Такие системы желательным образом должны иметь функции и свойства, которые специальным образом настраиваются с конкретными потребностями поддержки разнообразных игр и типов игровых автоматов, обеспечивая это эффективным, надежным и экономичным способом.

В дополнение к осуществлению связи между универсальной операционной системой и нестандартными устройствами в составе игрового автомата, такими как монетоприемники, мониторы, устройства проверки банкнот и т.п., было бы желательно обеспечить функции защиты, которые позволяют операционной системе проверять то, что код игры и другие данные не были изменены в ходе функционирования.

В патенте США 5643086 описана игровая система, обеспечивающая возможность аутентификации приложения или игровой программы, сохраненной в устройстве памяти (носителе данных), таком как CD-ROM (ПЗУ на компакт-диске), RAM (ОЗУ), ROM (ПЗУ) или другом устройстве с использованием методов хеширования и шифрования. Устройства памяти могут быть расположены в игровом автомате или могут быть внешними относительно игрового автомата. Такой способ верификации не позволит обнаружить какие-либо изменения, которые возникают в исполняемом коде, поскольку этот способ тестирует код, находящийся на носителе до его загрузки в ОЗУ. Система аутентификации основывается на использовании цифровой подписи и предусматривает хеширование всего набора данных до осуществления процесса шифрования и дешифрования. См. также патенты США 6106396 и 6149522.

Патентная заявка США № 09/949,021 от 7 сентября 2001 на «Шифрование в защищенной компьютеризованной игровой системе» раскрывает систему шифрования/аутентификации, в которой компьютеризованный игровой контроллер имеет процессор, память и энергонезависимую память и обеспечивает управление компьютеризованной игрой на ставки; и игровые данные, сохраненные в энергонезависимой памяти, причем игровые данные, сохраненные в энергонезависимой памяти, проверяются в процессе работы. Кроме того, раскрыта игровая система, содержащая энергонезависимую память, зашифрованный файл управления, сохраненный в энергонезависимой памяти, причем зашифрованный файл управления включает в себя набор имен программных файлов, дающих информацию команд, код аутентификации сообщений, уникальный для каждого программного файла, и ключ кода аутентификации сообщений; игровой контроллер, обеспечивающий возможность дешифрования зашифрованного файла управления и аутентификации файлов игровых программ в процессе работы игровой системы; и устройства игровой системы, осуществляющие связь с игровым контроллером через интерфейс игровой системы.

Эта система может дополнительно содержать процесс кода аутентификации сообщений, сохраненный в памяти, причем игровой контроллер аутентифицирует набор программных файлов путем применения процесса аутентификации сообщений с использованием программных файлов и ключа кода аутентификации сообщений для обеспечения набора дополнительных кодов аутентификации сообщений и сравнения кодов аутентификации сообщений из файла управления с дополнительными кодами аутентификации сообщений. Дополнительно система может иметь процесс аутентификации сообщений, сохраненный в ПЗУ. Также раскрыт считываемый компьютером носитель, имеющий исполняемые компьютером команды для выполнения способа подготовки набора игровых данных, обеспечивающего возможность аутентификации, включающего обеспечение набора игровых данных, определение кода аутентификации сообщений, уникального для набора игровых данных; и сохранение набора игровых данных и кода аутентификации сообщений; а также считываемый компьютером носитель, имеющий исполняемые компьютером команды для выполнения способа аутентификации игры, используемой в игровой системе, включающего прием зашифрованного файла управления; дешифрование зашифрованного файла управления для обеспечения файла управления, причем файл управления включает в себя набор имен программных файлов, обеспечивающих информацию команд, набор кодов аутентификации сообщений, включающий в себя код аутентификации сообщений, уникальный для каждого программного файла, и ключ кода аутентификации сообщений; и использование исходного файла управления для верификации аутентификации игры.

Имеется потребность в альтернативной архитектуре и способах обеспечения специфической для игр платформы, которая отличается защищенным хранением и верификацией игрового кода и других данных, обеспечивает возможность защищенного изменения игрового кода в компьютеризованной игровой системе на ставки и имеет возможность проверять то, что этот код не изменился в процессе работы игрового автомата.

В области обеспечения защищенности игровых автоматов также желательно, чтобы игровой программный код мог быть идентифицирован как сертифицированный или утвержденный, например, посредством различных комиссий по регулированию игр, таких как Комиссия по регулированию игр штата Невада, Комиссия по регулированию игр штата Нью-Джерси и других полномочных комиссий.

Настоящее изобретение обеспечивает архитектуру и способ обеспечения специфической для игр на ставки платформы, которая отличается защищенным хранением и верификацией игрового кода и других данных, обеспечивает возможность защищенного обмена игровым кодом в компьютеризованной игровой системе на ставки и/или сетевой системе и обеспечивает это способом, простым для реализации и управления. Некоторые варианты осуществления изобретения обеспечивают возможность идентифицировать игровой программный код как сертифицированный или утвержденный Комиссией по регулированию игр штата или другими регулирующими агентствами. Изобретение обеспечивает эти и другие функции с использованием методов шифрования, арифметических операций по модулю, хеш-функций и других криптографических методов. Эти криптографические компоненты используются совместно для создания способа, который обеспечивает идентификацию при интерактивном его применении и аутентификацию набора игровых данных при неинтерактивном применении.

В математических системах интерактивная проверка неформально рассматривается как протокол, реализуемый между двумя сторонами, при котором одна сторона, называемая доказывающей стороной, пытается доказать некоторый факт другой стороне, называемой верифицирующей стороной (верификатором). Интерактивная проверка обычно принимает форму протокола запроса-ответа, при котором доказывающая сторона и верифицирующая сторона обмениваются сообщениями, и верифицирующая сторона по результатам выполнения протокола выдает либо «принято», либо «отклонено». Помимо теоретического интереса интерактивные проверки нашли некоторые применения в криптографии и компьютерной защите, такие как идентификация и аутентификация. В этих ситуациях факт, требующий доказательства, обычно, но не всегда, связан с проверкой идентичности доказывающей стороны, например секретного ключа доказывающей стороны.

Для интерактивных проверок полезно иметь следующие свойства, особенно в криптографических приложениях.

Полнота. Верифицирующая сторона всегда принимает доказательство, если факт является истинным, и как доказывающая сторона, так и верифицирующая сторона следуют протоколу.

Нормальность (правильность). Верифицирующая сторона всегда отклоняет доказательство, если факт является ложным, при условии, что верифицирующая сторона следует протоколу.

Нулевое знание. Верифицирующая сторона не узнает ничего о доказываемом факте (за исключением того, что он корректен) от доказывающей стороны, чего он не мог бы узнать помимо доказывающей стороны, даже если верифицирующая сторона не следует протоколу (если доказывающая сторона следует). В интерактивном доказательстве с нулевым знанием верифицирующая сторона не сможет и позже доказать этот факт кому-либо еще. (Не все интерактивные доказательства имеют это свойство).

Типовой цикл или компонент доказательства с нулевым знанием состоит из сообщения «извещения» от доказывающей стороны, за которым следует запрос от верифицирующей стороны, и затем ответ на запрос от доказывающей стороны. Протокол может повторяться на нескольких циклах. На основе ответов доказывающей стороны на всех циклах верифицирующая сторона принимает решение, принять или отклонить доказательство.

В предпочтительном варианте осуществления настоящее изобретение обеспечивает способ аутентификации набора игровых данных, сохраненного в игровом автомате. Путем применения интерактивного способа доказательства в комбинации с односторонней хеш-функцией как набора игровых данных, так и сообщения (сообщений) извещения от доказывающей стороны набор игровых данных может быть аутентифицирован как исходящий от доказывающей стороны. Это осуществляется путем интерпретации значения хеш-функции как набора случайных запросов к доказывающей стороне, которые используются для совершения интерактивных проверок, не требуя присутствия верифицирующей стороны. Такая процедура называется неинтерактивным доказательством с нулевым знанием. Она содержит все элементы интерактивного доказательства с дополнением значения хеш-функции, интерпретированного указанным образом. Каждая пара запроса/ответа записывается и сохраняется вместе с набором игровых данных для обеспечения цифровой «метки аутентичности».

Краткое описание чертежей

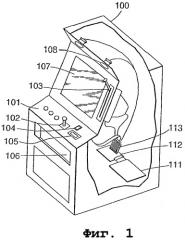
Фиг. 1 - компьютеризованное устройство для игры на ставки, которое может быть использовано для реализации некоторых вариантов осуществления изобретения.

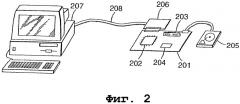
Фиг. 2 - диаграмма сетевого компьютера, соединенного с некоторыми компонентами, включающая в себя часть компьютеризованного устройства для игры на ставки, совместимого с некоторыми вариантами осуществления настоящего изобретения.

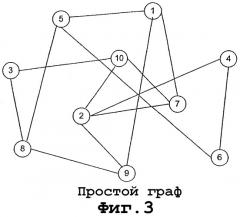
Фиг. 3 - граф, используемый для объяснения одного из примеров.

Фиг. 4 - диаграмма выступов, поясняющая описание процесса доказательства с нулевым знанием.

Фиг. 5 - блок-схема, соответствующая одному из ряда вариантов осуществления доказательства с нулевым знанием.

Фиг. 6 - cave (полость) - диаграмма для описания теории доказательства с нулевым знанием.

Детальное описание изобретения

Следующее описание содержит изложение того, как доказательство с нулевым знанием описано в работе Bruce Schneier, "Applied Cryptography", Second Edition, John Wiley& Sons, Inc., 1996. ISBN 0-471-12845-7. Функция доказательства с нулевым знанием в типовом случае обсуждается в терминах событий, причем cave-диаграмма, показанная на фиг. 6, представляет собой полезный инструмент для данного обсуждения. Предположим, что дверь между двумя пунктами, обозначенными С и D, может быть отперта только с использованием секретного ключа или пароля. Предполагается, что некоторое лицо (доказывающая сторона) знает секрет для отпирания двери, и оно может убедить наблюдателя (верифицирующую сторону), что ему известен секрет для отпирания двери, без необходимости открытия этого секрета наблюдателю с использованием доказательства с нулевым знанием. (Термин «нулевое знание» вытекает из того факта, что никакое знание секрета не выдается при представлении доказательства, таким образом, единичные итерации могут продолжаться нескончаемо долго).

Единичное доказательство с нулевым знанием может осуществляться следующим образом. Наблюдатель и лицо, владеющее секретом, как открыть дверь, начинают процедуру в точке А. Лицо, владеющее секретом, входит в полость в точку С или в точку D на диаграмме. После того как лицо, владеющее секретом, окажется на месте, оно вызывает наблюдателя для перемещения в точку В на диаграмме.

Наблюдатель затем выбирает случайным образом 1 или 0. Предварительно установлено, что если наблюдатель выбрал 0, то лицо, владеющее секретом, выйдет на левую сторону диаграммы, а если наблюдатель выбрал 1, то лицо, владеющее секретом, выйдет на правую сторону диаграммы. Наблюдатель выбирает число случайным образом, после того как лицо, владеющее секретом, окажется на месте в точке С или D. В результате наблюдатель знает, что единственным путем, когда результат может быть успешным с вероятностью 100%, является то, что если лицо, заявляющее, что оно знает секрет, действительно знает, как открыть дверь.

Заметим, что если это лицо на самом деле не знает секрета, вероятность равна точно 50%, что они смогут выйти из полости по правильному ходу, после того как наблюдатель выберет случайное число. Поэтому при повторении проверки с нулевым знанием n раз вероятность продолжения наличия успешного исхода, если лицо в действительности не знает секрета, становится 1/(2ⁿ). Если проверка с нулевым знанием повторяется 10 раз, то вероятность равна 1 из 1024, что лицо сможет «обмануть» протокол.

Второй момент, который необходимо отметить, заключается в том, что не имеет значения, сколько раз протокол повторяется, наблюдатель не получает знания о точном свойстве, в чем состоит секрет, чтобы открыть дверь. Лицо, которое знает секрет, может доказать наблюдателю, что оно действительно знает секрет, с любым уровнем определенности путем простого повторения протокола достаточное число раз.

Таким образом, ключевыми элементами доказательства с нулевым знанием являются следующие: 1) секрет, который может быть продемонстрирован без открытия его точного значения или его свойства, 2) извещение о конкретном выборе или проблеме, 3) случайный бит, выбранный после извещения, 4) возможность выполнить протокол независимо от того, какой бит выбран. Требуется, чтобы было невозможным успешно выполнить протокол со 100% вероятностью, если извещение не согласуется с выбранным случайным образом битом, если только секрет не известен. Выстраивая в цепочку множество итераций доказательства с нулевым знанием, вероятность того, что некто, не знающий секрет, сможет предсказать (передать извещение) правильный выбор до осуществления случайного выбора бита, может быть снижена.

Пример 1: Графическая реализация протокола доказательства с нулевым знанием

Для реализации доказательства с нулевым знанием с использованием математики следует обосновать доказательство известной проблемы, которую трудно решить. Здесь показаны два отличающихся варианта осуществления, хотя может быть множество возможных путем формирования протокола на основе ZKP.

Возможная реализация протокола доказательства с нулевым знанием основана на математической области теории графов. Граф, подобный показанному на фиг. 3, является совокупностью вершин (круги на чертеже), соединенных ребрами (линии на чертеже). Каждое ребро (линии на диаграмме) соединяют две вершины (круги на диаграмме).

При задании конкретного графа, если существует путь, который соединяет все вершины графа только однократно вдоль пути и завершается в исходной вершине, то такой путь известен как «гамильтонов цикл». На чертеже путь 2-4-6-5-1-9-8-3-10-7-2 является гамильтоновым циклом. Гамильтонов цикл является трудной проблемой для решения в случае чрезвычайно больших графов. Если только путь не является уже известным, время, которое потребовалось бы потратить на нахождение гамильтонова цикла в чрезвычайно большом графе, по математическому порядку величины соответствует квадрату числа вершин в графе.

Другая трудная проблема для решения в случае очень больших графов заключается в обеспечении того, чтобы два графа с одинаковым числом вершин и ребер были идентичны или изоморфны. То есть если бы граф случайным образом переупорядочивался и все вершины графа были бы заново обозначены другой последовательностью чисел, то очень трудно доказать, что два полученных в результате графа отличаются только обозначением вершин, если только заранее не известно отображение между вершинами графов.

Предположим, что гамильтонов цикл известен для конкретного чрезвычайно большого графа (наиболее вероятно путем создания графа из случайной функции). Это составляет секрет. Единственной итерацией доказательства с нулевым знанием данного секрета была бы следующая:

1) Доказывающая сторона публикует первоначальный граф. Доказывающая сторона утверждает, что ей известен гамильтонов цикл и может доказать его.

2) Доказывающая сторона случайным образом переупорядочивает граф и перенумеровывает все вершины.

3) Доказывающая сторона извещает о решении для нового графа. Имеются различные криптографические методы для извещения о секрете без раскрытия секрета, с использованием симметричного шифрования, шифрования открытым ключом или четной односторонней хеш-функции. Не имеет значения, какой из них использован на данном этапе, если желательная цель извещения о новом графе реализована на этом этапе.

4) Верифицирующая сторона выбирает случайным образом бит 0 или 1.

а) Если выбранный бит есть 0, то доказывающая сторона показывает, что новый граф изоморфен старому графу.

b) Если выбранный бит есть 1, то доказывающая сторона показывает гамильтонов цикл для нового графа.

Заметим, что для каждого цикла этого протокола, если мошенник в действительности не знает гамильтонова цикла исходного графа, то он должен был бы прогнозировать, выберет ли верифицирующая сторона 0 или 1 на этапе 4, прежде чем извещать на этапе 2. Если мошенник ожидал выбора 0, то он случайным образом переупорядочил бы исходный граф, но не смог бы найти гамильтонов цикл в новом графе, если вместо этого была выбрана 1, поскольку он не знает первоначальный секрет. Если мошенник ожидал выбора 1, то он мог бы генерировать новый граф с гамильтоновым циклом в нем, с тем же числом вершин и ребер, что и в исходном графе, но он не смог бы обеспечить отображение вершин для доказательства, что два графа были изоморфны, если вместо этого был выбран 0. Кроме того, поскольку новый граф является случайным относительно исходного графа и только одно из двух решений дается с каждой итерацией доказательства с нулевым знанием, то отсутствует утечка информации, относящейся к первоначальному секрету. Протокол может быть повторен любое число раз, причем с каждой итерацией уменьшается вероятность того, что кто-то сможет успешно предсказать случайные биты для всех этапов.

Пример 2: Протокол доказательства с нулевым знанием с использованием разложения на множители, возведения в квадрат и арифметических операций по модулю

Эта процедура основывается на опубликованной в Интернете статье о доказательствах с нулевым знанием автора Bennett Yee из Калифорнийского университета, Сан-Диего.

Предположим, что имеются два больших простых числа, произведение которых условно обозначено n. Если для этих двух простых чисел выбраны достаточно большие значения, то в вычислительном смысле становится практически не реализуемым разложить на множители это число. Кроме того, при задании любого числа нахождение квадратного корня от этого числа по модулю n равным образом оказывается практически нереализуемым в вычислительном смысле. Показано, что разложение на множители числа n эквивалентно вычислению квадратного корня из числа по модулю n.

Для данной реализации доказывающая сторона выбирает случайное число s. Число s становится секретом. Следующие этапы описывают протокол доказательства с нулевым знанием для данной реализации.

Доказывающая сторона публикует значение v=s² mod n. Поскольку математически очень сложно вычислить корень квадратный из этого значения по модулю n (см. выше), то секрет остается скрытым.

Доказывающая сторона выбирает случайное число r.

Доказывающая сторона извещает о значении x=r² mod n и посылает это значение верифицирующей стороне. Верифицирующая сторона выбирает случайное число 0 или 1.

а) Если выбранный бит есть 0, то доказывающая сторона посылает y=r верифицирующей стороне; и верифицирующая сторона проверяет, чтобы убедиться, согласовано ли y² mod n со значением x=r² mod n, о котором доказывающая сторона известила на этапе 3.

b) Если выбранный бит есть 1, то доказывающая сторона посылает y=r s верифицирующей стороне, и верифицирующая сторона проверяет, согласуется ли y² mod n с значением xv.

Заметим, что если мошенник не знает секрет, то он смог бы только успешно завершить протокол с вероятностью 50%. Если мошенник ожидал, что выбрано 0, то он мог бы только следовать протоколу и иметь успех, если только в действительности не было бы выбрано 1, и в этом случае он не смог бы предоставить значение y=rs верифицирующей стороне, поскольку секрет s неизвестен. С другой стороны, если мошенник ожидал, что выбрана 1, он смог бы выбрать любое случайное число t и послать x=t²/v в верифицирующей стороне, если только 0 не был в действительности выбран, и в этом случае он не смог бы вычислить квадратный корень из v mod n в знаменателе.

Вновь этот протокол доказательства с нулевым знанием может быть повторен любое число раз без открытия секрета верифицирующей стороне. Каждая итерация снижает вероятность того, что кто-либо, кто не знает секрет, сможет успешно обмануть протокол.

Ниже приведен пример того, что представляет собой этот протокол с использованием 128-битовых чисел:

и пакеты могут продолжаться таким образом до бесконечности, причем каждый цикл снижает вероятность того, что посторонний мошенник сможет искусственно сформировать пакеты.

До сих пор описание фокусировалось на объяснении того, что понимается под доказательствами с нулевым знанием, и на представлении некоторых примеров, что может представлять собой протокол на основе ZKP. Последующие разделы описывают то, каким образом можно адаптировать любой протокол доказательства с нулевым знанием для использования при аутентификации наборов данных игр казино и игровых данных и игровых программ.

Хеш-функция представляет собой функцию, которая берет битовую последовательность переменной длины и вычисляет из нее более короткую битовую идентифицирующую последовательность («отпечаток пальца») фиксированной длины. Это значение хеш-функции может быть использовано для различных целей в компьютерной области.

Односторонняя хеш-функция является специальной хеш-функцией, которая вычисляет значение хеш-функции из битовой последовательности переменной длины таким путем, что невозможно предсказать результат для конкретных входных данных. Очень трудно генерировать или модифицировать последовательность битов, чтобы ее можно было хешировать для получения желательного значения.

Путем использования односторонней хеш-функции любой алгоритм доказательства с нулевым знанием может быть адаптирован для осуществления аутентификации. Для того чтобы показать, как это делается, напомним, что каждый алгоритм, основанный на доказательстве с нулевым знанием, должен содержать для каждой итерации: 1) секрет, который может быть предоставлен без раскрытия его точного значения или свойства; 2) извещение о конкретном выборе или проблеме (случайная перестановка); 3)случайный бит, который выбран после извещения, и 4) возможность завершения протокола независимо от того, какой бит выбран. В одном из примеров, приведенных выше, секретом была нумерация вершин графа для задачи нахождения гамильтонова цикла, а во втором примере - выбранная битовая последовательность. В обоих случаях секрет был замаскирован генерацией случайной перестановки перед каждым доказательством с нулевым знанием, чтобы не открыть секрет. Часть доказательства с нулевым знанием в каждом примере для доказывающей стороны заключалась в открытии случайного упорядочения, если соответствующий случайный бит был выбран верифицирующей стороной.

Обращаясь к фиг. 5, можно видеть, что если набор данных используется в качестве входных данных для односторонней хеш-функции, вместе с проверкой существования секрета и случайными перестановками из каждого цикла доказательства с нулевым знанием вырабатывается значение хеш-функции, которое зависит не только от набора данных, но и от случайных извещений о строго определенных проблемах ZKP (которые могут, таким образом, описываться как случайные перестановки первоначальной задачи). Это значение хеш-функции может затем использоваться как случайная битовая строка, которая выводится из входных данных. Иными словами, вместо осуществления доказательства с нулевым знанием по интерактивной процедуре, когда верифицирующая сторона случайным образом выбирает 1 или 0, можно использовать шаблон единиц или нулей, который образует эту хэш-функцию из односторонней хеш-функции, для завершения протокола ZKP по неинтерактивной процедуре. Поскольку результат значения хеш-функции невозможно предсказать, доказывающая сторона должна быть готова решать строго определенные задачи для каждого доказательства с нулевым знанием, и единственны