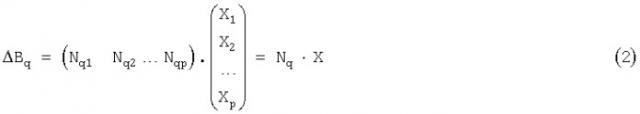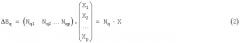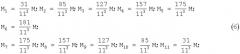Способ измерения магнитного момента крупногабаритного тела удлиненной формы

Способ измерения магнитного момента крупногабаритного тела удлиненной формы

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерения магнитного момента (ММ), в частности крупногабаритного тела удлиненной формы (например корабля). Разумеется, речь идет о косвенном измерении ММ тела.

Известен двухточечный магнитометрический метод измерения ММ [Семенов В.Г. и Сонина В.Э. Анализ методов измерения магнитных моментов // Метрология, 1992, №8, с.7]. Этот метод применяется для измерения ММ крупногабаритных тел благодаря своей простоте и оперативности. Однако, как показано в статье [Семенов и Сонина, 1992, с.32, 35], результирующая погрешность двухточечного метода достаточно велика, особенно для тела удлиненной формы (20-30%). Причем в результирующей погрешности (16-23%) преобладает методическая погрешность или погрешность от недипольности тела (10-16%).

Известен также двенадцатиточечный магнитометрический метод измерения ММ [Семенов В.Г. и Сонина В.Э. Анализ методов измерения магнитных моментов // Метрология, 1992, №8, с.10], который обеспечивает повышенную точность (2,7-3,4%) за счет существенного снижения методической составляющей погрешности (0,9-1,7%). Но из-за большого числа точек, особым образом располагаемых вокруг испытуемого тела, метод не применим для крупногабаритных тел. Для малогабаритных тел этот метод может быть применен. Примером малогабаритного тела является магнитная модель корабля в масштабе 1/25-1/100.

Известен также метод измерения ММ судов и кораблей [В.И.Большаков и др. Оценка магнитного состояния судна по результатам измерения его магнитного поля // Труды Второй международной конференции по судостроению. Секция Е. Физические поля судов и океана. 1998, т.2, c.12-16. СПб.]. Точнее, эта методика направлена на осуществление контроля магнитного поля судна в плоскости на глубине, равной полуширине судна, а определение ММ по данной методике получается как вторичный результат. Оказалось, что данный метод измерения ММ имеет плохую точность. Причины плохой точности измерения ММ остались непонятными, но основную задачу - контроль поля судна на заданной плоскости - авторы методики решили удовлетворительно.

Процитируем отрывок из статьи [Большаков и др. 1998, с.14]:

"Как показали исследования [4], такая модель на расстояниях, порядка полуширины судна, адекватно описывает его магнитное поле. Этот отрезок разбивается на 8-10 участков приблизительно равной длины". В этом отрывке, как будет показано ниже (см. таблицу 5), кроется разгадка плохой точности измерения ММ по известному способу.

По совокупности существенных признаков в качестве ближайшего аналога заявляемого способа принят способ измерения ММ крупногабаритного тела удлиненной формы [Большаков и др. 1998, с.14].

Известный способ измерения ММ крупногабаритного тела удлиненной формы [Большаков и др. 1998, с.14] включает измерения параметров магнитного поля тела во внешних от тела точках, измерения расстояний между этими точками и центром тела, разбиение тела на продольные участки, составление и решение системы линейных уравнений относительно ММ участков и определение результата как суммы ММ участков.

Причиной, препятствующей достижению указанного ниже технического результата при использовании известного способа, являются неправильные рекомендации по выбору расстояния и числа участков разбиения тела при измерении ММ.

Задачей, на решение которой направлено заявляемое изобретение, является повышение точности измерения ММ крупногабаритного тела удлиненной формы.

Технический результат, получаемый при осуществлении изобретения, заключается в выборе при измерении такого расстояния и такого числа участков разбиения, которые соответствуют повышенной точности измерения ММ. Ожидается повышение точности не менее чем на порядок на расстояниях измерения 0.35-0.5 длины тела L при числе участков p=4-12.

Указанный технический результат достигается тем, что в заявляемом способе измерения магнитного момента (ММ) крупногабаритного тела удлиненной формы путем измерения параметров индукции магнитного поля тела во внешних точках и расстояний между точками и центром тела, включая удаление или минимальное расстояние между датчиком параметров поля и центром тела, путем разбиения тела на продольные участки, составления и решения системы линейных уравнений относительно ММ участков и определения результата как суммы ММ участков, в отличие от известного способа, измерение ММ выполняют при удалении и числе участков, обеспечивающих повышенную точность измерения ММ, для определения которых составляют для тел одного класса расчетную магнитную модель с заданным ММ и моделируют измерение на компьютере для заданной конфигурации точек измерения параметров магнитного поля тела и заданных СКО погрешностей средств измерения параметров индукции магнитного поля и расстояний, затем вычисляют разность между моделированным и заданным значениями ММ, находят ряд статистических оценок разностей при разных удалениях и числах участков и выбирают удаление и число участков, соответствующие области наименьшей оценки.

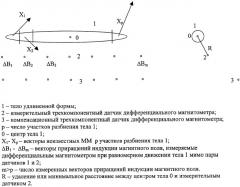
На чертеже изображена одна из возможных схем измерения ММ тела удлиненной формы по заявляемому способу. Схема на чертеже включает тело удлиненной формы 1, трехкомпонентные измерительный 2 и компенсационный 3 датчики дифференциального магнитометра.

Заявляемый способ осуществляется следующим образом. Тело 1 мысленно разбивают на p участков равной длины. Каждому участку приписывают свой неизвестный ММ X₁-Х_р. Тело 1 равномерно передвигают своим ходом, например, по прямолинейной траектории мимо измерительного 2 и компенсационного 3 датчиков дифференциального магнитометра, которым измеряют m приращений индукции магнитного поля тела 1 в разнесенных точках 1, 2, 3...q...m-1, m. Каждый участок тела 1 с MM Xs создает в точке q свою долю приращения индукции магнитного поля между точками 2 и 3, описываемого соотношением [Семенов В.Г. и Сонина В.Э. 1992, с.7]

где ΔB_23qs - вектор-столбец приращения магнитной индукции между точками 2 и 3, Тл;

n_2qs, n_2qs, n_3qs, n_3qs - диады из единичных векторов направлений радиус-векторов между точками 2q и s и точками 3q и s;

R_2qs, R_3qs - модули радиус-векторов между точками 1q и s и точками 2q и s, м;

X_s - вектор-столбец ММ в точке s, Ам²;

N_qs - матрица 3×3.

Все приращение индукции в точке q запишется как

где ΔB_q - полное приращение индукции в точке q между измерительным и компенсационным датчиками - матрица 3×1;

N_q - матрица размера 3×3р,

Х - одностолбцовая матрица 3р×1.

Для m точек измерений приращений магнитной индукции из (2) получим

где ΔB - одностолбцовая матрица приращений магнитной индукции размера 3m×1;

N - прямоугольная матрица размера 3m×3p, называемая координатной матрицей.

Систему 3m линейных алгебраических уравнений (3) можно решить относительно 3p неизвестных, если m равно или больше р. Решение (3) по методу наименьших квадратов имеет вид

где N^T - транспонированная матрица N;

(N^T·N)^-1 - обратная матрица от квадратной матрицы (N^T·N) размера 3р×3р.

Решение (4) существует, если существует обратная матрица (N^T·N)^-1. Далее по определенной с помощью (4) одностолбцовой матрице X находят ММ тела

где - результат (косвенного) измерения ММ тела.

Примечание. Заявляемый способ применим не только к схеме дифференциального магнитометра с датчиками 2 и 3, изображенными на чертеже. Он применим также к схеме из одного датчика 2 (или нескольких датчиков 2) без компенсационного датчика 3. В таком случае в датчике 2 в отсутствие тела 1 компенсируют поле Земли и корректируют нули магнитометра, после чего приближают тело 1 и измеряют индукцию магнитного поля тела на фоне компенсированной постоянной части поля Земли. Хотя в обоих случаях термин "приращение индукции магнитного поля" правилен, в нормативной документации по магнитным измерениям он отсутствует. В документации рекомендуется термин "измерение индукции магнитного поля", который не соответствует схеме на чертеже. Для того, чтобы охватить обе схемы измерения с компенсационным датчиком 3 и без него, не вступая в противоречие с рекомендациями нормативной документации, в описании заявляемого способа наряду с термином "измерение приращения индукции магнитного поля" иногда используется равнозначный термин "измерение параметров индукции магнитного поля". В формуле изобретения используется термин "измерение параметров индукции магнитного поля".

До сих пор заявляемый способ повторял известный. Далее начинаются отличия. Начнем с того, что определяемый соотношением (5) результат измерения ММ не будет точным даже при абсолютно точных измерениях приращений индукции и расстояний, т.е. при абсолютно точных элементах матрицы N и вектор-столбца ΔB. Точность результата измерения ММ исключительно сильно зависит от выбора удаления тела R (см. фиг.1) и выбора числа зон разбиения. В заявляемом способе выбор R был продиктован необходимостью контроля магнитных полей судна в заданной горизонтальной плоскости под судном на удалении по вертикали от ватерлинии "порядка полуширины судна" [Большаков и др. 1998, с.14]. Такое близкое к телу расстояние измерения (полуширина или ширина) невыгодно с точки зрения точности измерения ММ тела (см. таблицу 5). Для выбора удаления и числа участков, выгодных для измерения ММ, в заявляемом способе используют расчетную магнитную модель тела с известным точным значением ММ модели и с распределением ММ по длине, близким к распределению натурного тела. В первом приближении это может быть равномерно намагниченный эллипсоид, ориентированный в геомагнитном поле аналогично ориентации натурного тела. Например, известно, что некоторое тело с продольной осью в направлении Север - Юг имеет ММ, равный M=[M_x;M_y;M_z]. Если тело аппроксимировать равномерно намагниченным эллипсоидом вращения с полуосями L/2, B/2, Н/2, где L - длина, В - ширина, Н - высота корпуса тела, и разбить тело, например, на 11 участков, то MM участков окажутся следующими:

При разбиении эллипсоида на участки равной длины объемы участков нарастают от концов к центру эллипсоида, пропорционально объемам изменяются коэффициенты в числителях ММ участков (6). Обратим внимание, что сумма ММ всех участков равна ММ тела, т.е. М, так как 31+85+127+157+175+181+175+157+127+85+31=11³.

Имея известные ММ участков (6), по соотношению (1) с помощью компьютерной вычислительной программы, например МатЛаб, рассчитывают приращения индукции магнитного поля, созданного моделью тела 1 в заданной совокупности точек измерения приращений. К приращениям с помощью МатЛаб добавляют случайные величины с нулевым средним и СКО σ_В, равным СКО аддитивной инструментальной погрешности дифференциального магнитометра с измерительным 2 и компенсационным 3 датчиками. Для типовых магнитометров при удалении датчиков на расстояние не менее 8 км от линий электротяги на постоянном токе σ_В лежит в пределах от 0.1 до 0.5 нТл в зависимости от идентичности измерительного и компенсационного датчиков и тщательности углового согласования их магниточувствительных осей. Кроме того, к заданным расстояниям, по которым вычисляют координатную матрицу N, добавляют случайные погрешности с нулевым средним и СКО σ_R, соответствующим СКО средств измерения расстояния. Для типовых средств измерения расстояния σ_R≤1 м. Затем решают систему (4) и рассчитывают ММ модели тела (5), отягощенный методической (систематической) и двумя случайными инструментальными погрешностями компьютерного моделирования процесса измерения ММ от погрешностей измерения параметров магнитного поля и расстояний. МатЛаб повторяет процедуру решения 30-10³ раз, обрабатывает всю совокупность результатов и находит составляющие и результирующую оценки погрешности (моделированного) измерения ММ. Важно, что МатЛаб не только моделирует сами погрешности, но и находит статистические оценки этих погрешностей. Отличие между погрешностью и оценкой ее в том, что погрешность содержит случайную (неопределенную) величину, а оценка этой погрешности (если она достаточно репрезентативна), представляет собой детерминированную (определенную или неслучайную) величину.

Запишем среднюю компоненту относительной (систематической) методической погрешности в виде

где Х_МИx Х_МИy, Х_МИz - компоненты результата (моделированного) измерения ММ модели по уравнениям (4)-(5) при точных вектор-столбце приращений индукции ΔВ и координатной матрице N;

М_x, М_y, М_z - компоненты ММ модели;

|М|- модуль ММ модели.

(В заявляемом способе компоненты и модуль ММ модели известны).

Обозначим:

σ_MB - СКО или оценка погрешностей измерения ММ от погрешностей измерения приращений магнитной индукции;

σ_MR - СКО или оценка погрешностей измерения ММ от погрешностей измерения расстояний между центром тела и точками измерения приращений.

Тогда оценку относительной результирующей погрешности при доверительной вероятности 0.95 можно представить в виде

[А.Н.Зайдель. Погрешности измерения физических величин. Наука, 1985, с.61-66].

Оценку результирующей погрешности можно было бы выбрать иначе, например, при доверительной вероятности 0.99

или при доверительной вероятности 0.997

[Guide to the expression of uncertainty in measurement ISO Geneva. Руководство по выражению неопределенности измерения. ВНИИМ, СПб, 1999, с.71].

Примеры расчета оценок погрешностей измерения ММ даны в таблицах 1-5. Результаты представлены в функции удаления тела, отнесенного к его длине, при σ_В=0.5 нТл, σ_R=1 м для модели тела (6), числе участков разбиения тела p=1, 2, 4, 6, 8, 10, 12 при 32 точках измерения приращений, равномерно распределенных по отрезку прямой линии длиной 1.25 L.

Таблица 1Методическая составляющая погрешности δМмет
R/L	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5
p=1	.52	.50	.46	.41	.36	.32	.28	.24	.22	.19
p=2	.52	.47	.43	.39	.34	.30	.26	.22	.19	.15
p=4	.50	.45	.38	.29	.20	.13	.07	.03	.016	.008
p=6	.46	.42	.27	.12	.026	.006	.003	.0014	.0007	.0004
p=8	.48	.37	.12	.009	.0012	.0002	.0001	.0000	.0000	.0000
p=10	.60	.33	.013	.0003	.0000	.0000	.0000	.0000	.0000	.0000
p=12	.63	.25	.0004	.0001	.0000	.0000	.0000	.0000	.0000	.0000

Методическая погрешность δМ_мет неслучайная величина, поэтому она совпадает со своей оценкой. Как видно из таблицы 1, δМ_мет велика вблизи тела, но с удалением она снижается тем быстрее, чем больше число участков разбиения р.

Таблица 2Оценка (СКО) инструментальной погрешности σМВ/|М|
R/L	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65
p=1	.0001	.0001	.0002	.0003	.0005	.0007	.0009	.0011	.0015	.0018
p=2	.0001	.0002	.0003	.0005	.0008	.0012	.0016	.0022	.0029	.0039
p=4	.0002	.0005	.0012	.0023	.0035	.0053	.0073	.0099	.0128	.0163
p=6	.0007	.0015	.0024	.0034	.0050	.0066	.0091	.0130	.0179	.0265
p=8	.0011	.0019	.0029	.0043	.0058	.0083	.0130	.0191	.0298	.0488
p=10	.0013	.0021	.0032	.0047	.0075	.0117	.0195	.0327	.0.554	.1093
p=12	.0014	.0023	.0036	.0058	.0104	.0192	.0365	.0678	.1384	.2712

В отличие от методической погрешности оценка σ_МВ/|М| нарастает с удалением от тела тем раньше и круче, чем больше р.

Таблица 3Оценка (СКО) инструментальной погрешности σMR/|М|
R/L	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65
p=1	.0111	.0105	.0103	.0094	.0092	.0086	.0083	.0088	.0076	.0072
p=2	.0145	.0127	.0112	.0101	.0096	.0082	.0078	.0074	.0065	.0062
p=4	.0162	.0144	.0122	.0105	.0104	.0112	.0100	.0103	.0089	.0089
p=6	.0208	.0219	.0178	.0146	.0124	.0115	.0104	.0091	.0088	.0081
p=8	.0310	.0229	.0196	.0140	.0128	.0106	.0102	.0087	.0084	.0080
p=10	.0331	.0209	.0149	.0140	.0122	.0102	.0102	.0085	.0076	.0068
p=12	.0323	.0200	.0150	.0137	.0117	.0098	.0088	.0085	.0077	.0063

Как видно из таблицы 3, оценка σ_MR/|М| монотонно уменьшается с удалением от тела.

Вблизи от тела она тем больше, чем больше p, с удалением от тела зависимость от p исчезает. Некоторые отклонения от этого правила среди данных таблицы, по-видимому, объясняются недостаточной репрезентативностью оценок из-за малого объема выборок (100).

Таблица 4Оценки результирующих погрешностей δМ0.95
R/L	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65	0.7
p=1	.3831	.3374	.2959	.2620	.2330	.2096	.1897	.1729	.1585	.1465
p-2	.3677	.3210	.2791	.2434	.2110	.1848	.1626	.1429	.1273	.1143
p=4	.2308	.1500	.0905	.0562	.0408	.0317	.0326	.0335	.0388	.0441
p=6	.0696	.0418	.0329	.0311	.0251	.0272	.0318	.0400	.0554	.0787
p=8	.0473	.0398	.0293	.0281	.0270	,0329	.0421	.0619	.0988	.1659
p=10	.0420	.0304	.0293	.0272	.0321	.0440	.0676	.1118	.2190	.4027
p=12	.0402	.0310	.0298	.0313	.0431	.0752	.1367	.2774	.5434	1.148

Как видно из таблицы 4, при некоторых R/L оценки δМ_0.95 для p=4-12 обращаются в минимумы (отмечены полужирным шрифтом), для p=1-2 минимумы не поместились. Они представлены ниже в таблице 5.

Оптимальные удаления R/L, числа участков p и соответствующие минимумы оценок δМ_0.95 и δМ_0.997 по заявляемому способу в сравнении с аналогичными оценками при рекомендациях известного способа (R/L=0.1 и p=8-10).

Таблица 5
R/L	0.1		0.35	0.4	0.45	0.5		0.95		1.3
p-1										.088
p-2								.086
p=4						.032
p=6					.025
p=8				.025
p=10				.027
p=12			.030
по известному способу (δМ0.95)
p=8	.44
p=10	.42
по заявляемому способу (δМ0.997)
p=4						.046
p=6						.042
p=8				.039
p=10			.041
p=12			.042
по известному способу (δМ0.997)
p=8	.47
p=10	.47

Как видно из таблицы 5, при существующем уровне средств измерения приращений индукции и расстояний (σ_B=0.5 нТл, σ_R=1 м) заявляемый способ обеспечивает повышение точности измерения ММ не менее чем в 10 раз по сравнению с известным способом. Кроме того, заявляемый способ обеспечивает большую свободу выбора удалений и числа участков p за счет контроля за поведением оценки в районе минимума. Например, как показано в таблице 5, в рассматриваемом случае наилучший режим измерения R/L=0.4 и p=8. Допустим режим, например R/L=0.35 и p=10 или R/L=0.5 и p=6, так как соответствующие оценки 0.041 и 0.042 мало отличаются от минимума 0.039.

Как видно из таблиц 1-5, в заявляемом способе доля методической составляющей в общей оценке погрешности исключительно мала. В известном способе она преобладает. Это означает, что если повысить точность средств измерения параметров магнитного поля и расстояния, например, в 5 раз (σ_B=0.1 нТл, σ_R=0.2 м), то заявляемый способ даст почти пятикратное повышение точности измерения ММ, а в известном способе точность измерения ММ не изменится.

Поскольку доля методической погрешности в заявляемом способе мала, то отклонения расчетной модели от натуры не приводят к существенной потере точности измерения ММ. Это еще одна важная особенность заявляемого способа.

Способ измерения магнитного момента (ММ) крупногабаритного тела удлиненной формы путем измерения параметров индукции магнитного поля тела во внешних точках и расстояний между точками и центром тела, включая удаление или минимальное расстояние между датчиком параметров поля и центром тела, путем разбиения тела на продольные участки, составления и решения системы линейных уравнений относительно ММ участков и определения результата как суммы ММ участков, отличающийся тем, что измерение ММ выполняют при удалении и числе участков, обеспечивающих повышенную точность измерения ММ, для определения которых составляют для тел одного класса расчетную магнитную модель с заданным ММ и моделируют измерение на компьютере для заданной конфигурации точек измерения параметров магнитного поля тела и заданных среднеквадратических отклонений погрешностей средств измерения параметров индукции магнитного поля и расстояний, затем вычисляют разность между моделированным и заданным значениями ММ, находят ряд статистических оценок разностей при разных удалениях и числах участков и выбирают удаление и число участков, соответствующие области наименьшей оценки.