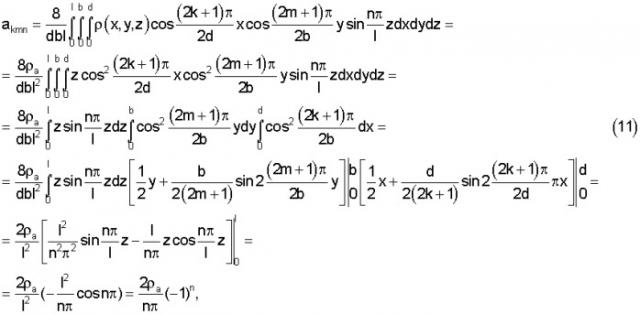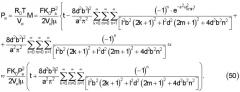Способ определения параметров пористости материалов

Способ определения параметров пористости материалов

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может быть использовано при оценке качества пористых материалов, например керамики, металлокерамики.

Известен способ определения параметров пористости материалов (Патент РФ № 2186365, кл. G01N 15/08, 2002 г.).

Согласно этому способу ячейку, состоящую из двух камер (рабочей и измерительной), разделенных испытуемым образцом, вакуумируют. Рабочую камеру соединяют с атмосферой. Подают газ в рабочую камеру. Регистрируют изменение давления, температуру, приращение давления в измерительной камере за определенный промежуток времени. Сравнивают каждое приращение давления с предыдущим и фиксируют время, когда они окажутся равны, измеряют величину давления в измерительной камере за фиксированное время и определяют коэффициенты фильтрации (К_ф), проницаемости (К₀), диффузии (D) и растворимости (К_г).

Недостатком данного способа является то, что способ не позволяет определить параметры пористости для труднопроницаемых материалов. Кроме того, известный способ не позволяет определить коэффициент пористости материалов.

Наиболее близким по технической сущности к предлагаемому решению является способ определения параметров пористости материалов (Патент РФ № 2235308, кл. G01N 15/08, 2004 г.).

Согласно этому способу образец помещают в ячейку, разделяя ее на рабочую и измерительную камеры. Камеры вакуумируют. Рабочую камеру соединяют с атмосферой. Регистрируют изменение давления, температуру и приращение давления за определенный промежуток времени в измерительной камере. Осуществляют выравнивание каждого последующего приращения давления с предыдущим. Фиксируют время, при котором величина последующего приращения давления окажется равной предыдущему, измеряют величину давления в измерительной камере за фиксированное время. Измеряют температуру в рабочей камере, осуществляют выравнивание ее с температурой в измерительной камере и поддерживают их равными друг другу в течение всего процесса. Коэффициенты фильтрации (К_ф), проницаемости (К₀), диффузии (D), растворимости (константа Генри - К_г) и пористости (П) определяют из соотношений:

здесь V_n - номинальный объем измерительной камеры;

Р_а - атмосферное давление;

F - площадь образца, разделяющего камеры;

ν - коэффициент кинематической вязкости;

μ - коэффициент динамической вязкости;

Р_c, t_c - давление и время в измерительной камере при равенстве предыдущего и последующего приращений давления;

Р_n, t_n - текущее значение давления и времени, t_n>t_c;

l - толщина исследуемого образца.

Недостатком данного способа является то, что способ обладает не высокой точностью измерений, так как процесс фильтрации происходит только вдоль одной оси, т.е. рассматривается одномерная модель течения газа через материал.

Задачей, решаемой изобретением, является повышение точности способа путем обеспечения возможности исследования трехмерной модели течения газа через пористый материал.

Это достигается тем, что в способе, заключающемся в том, что из герметично соединенной с материалом измерительной камеры откачивают воздух, регистрируют температуру и измеряют величину давления в измерительной камере. Увеличивают объем измерительной камеры, осуществляя тем самым разрежение газа до давления, обеспечивающего возможность молекулярного течения через поры контролируемого материала. Измеряют объем измерительной камеры. Фиксируют остаточное давление газа и время начала процесса течения газа через материал, а коэффициенты фильтрации (К_ф), проницаемости (К₀), диффузии (D), растворимости (константа Генри - К_г) и пористости (П) определяют из соотношений:

- коэффициент растворимости:

- коэффициент фильтрации:

- коэффициент пористости:

- коэффициент газопроницаемости

- коэффициент диффузии:

где или .

где V_и - объем газа, протекающего в единицу времени t_и при давлении Р_и в измерительную камеру;

F - площадь контролируемого изделия, ограниченная измерительной камерой;

μ - коэффициент динамической вязкости;

Р_c, t_c - давление и время в измерительной камере, соответствующие переходу от кнудсеновского к ламинарному режиму течения газа;

Р_и, t_и - текущее значение давления и времени, t_и>t_c;

P_a - атмосферное давление;

ν - коэффициент кинематической вязкости;

l - длина контролируемого материала;

b - ширина материала, ограниченная измерительной камерой;

d - толщина материала, ограниченная измерительной камерой.

Введение измерения давления, соответствующего разрежению газа до величины давления, обеспечивающего молекулярное течение газа через поры материала, измерения в этот момент объема измерительной камеры и осуществление начала контроля с момента окончания процесса разрежения обеспечивает возможность исследования трехмерной модели течения газа через материал, что подтверждается следующим.

Основными уравнениями, характеризующими процесс, являются:

- уравнение Дарси:

- уравнения Фика для стационарного потока:

- уравнения Фика для нестационарного потока:

- уравнение Лейбензона для изометрической фильтрации:

- добавочное уравнение:

где ρ - плотность газа, q - поток газа в единицу времени, К_ф - коэффициент фильтрации, l - линейный размер в направлении фильтрации, Р - давление газа, ΔР - перепад давления в материале (потери напора), D - коэффициент диффузии, ▿Р - модуль градиента давления в исследуемом материале, ▿ρ - модуль градиента концентрации в исследуемом материале, К₀ - коэффициент проницаемости, П - коэффициент пористости, μ - коэффициент динамической вязкости, t - время, Р_а - атмосферное давление, V_и - объем газа, П - коэффициент пористости, μ - коэффициент динамической вязкости, R₀ - газовая постоянная, Т - температура газа, F - площадь контролируемого изделия, ограниченная измерительной камерой, Р_и - текущее значение давления газа.

Для трехмерного случая (движение газа через пористый материал длиной l, шириной b и толщиной d) уравнения (2)-(4) примут вид:

- уравнения Фика для стационарного потока:

- уравнения Фика для нестационарного потока:

- уравнение Лейбензона:

где x, y, z - координаты.

Решения уравнения (7) ρ(x, y, z, t) должно удовлетворять следующим граничным и начальным условиям:

0<x<d, 0<y<b, 0<z<l, t>0,

ρ(x, y, z, 0)= ρ(x, y, z), 0<x<d, 0<y<b, 0<z<l,

Решением уравнения (7), удовлетворяющим граничным и начальным условиям (9), является функция:

В качестве НУ возьмем функцию:

где k=0, 1, 2, 3..., m=0, 1, 2, 3...,

ρ_a - плотность газа при атмосферном давлении.

Тогда

где n=1, 2, 3...,

Таким образом, решением уравнения (7) является следующая функция, описывающая плотность ρ(x, y, z, t), удовлетворяющая граничным и начальным условиям (9):

Введем новую переменную ρ₁(x, y, z, t), равную

удовлетворяющую следующим граничным и начальным условиям:

Тогда

Введем следующее преобразование координат:

вызванное течением газа (воздуха) из окружающей среды через контролируемый материал в камеру с разреженным газом.

В этом случае вместо (16) получаем

где индексы при ρ и х, y, z опущены.

Уравнение Фика для стационарного потока имеет вид:

Выражение (19) подставляем в левую часть добавочного уравнения (5), после чего получаем:

Или

Интегрируя уравнение (21) в пределах от 0 до t, получаем:

Второе слагаемое в (22) быстро затухает и при им можно пренебречь.

Тогда

где ρ_а=К_Г·Р_а.

На линейном участке вместо Р_и подставим Р_и-Р_с, которое возможно при t_и-t_c соответственно.

Таким образом

где

где Р_и, t_и - текущее значение давления и времени, t_и>t_c.

Рассмотрим различные варианты соотношений l, d, b.

Полагая в равенстве (23) d=∞, b=∞, получаем выражение для одномерного случая, т.е.

т.к.

то

где

Полагая, что в (23) b=∞, получаем результат при двумерном случае:

Для случая вместо выражения (23) получаем:

Если в выражении (28) d=b, то оно примет вид:

где

Рассмотрим случай, когда газовый поток протекает в цилиндрическом пространстве.

В этом случае d=b=2r.

Тогда вместо выражения (23) получаем:

При большой длине цилиндра получаем:

где

Если то вместо (23) получаем:

где

Таким образом, имеем следующие возможные выражения для времени t_c:

- для трехмерной модели

для твердых цилиндрических тел большой длины, когда

Для одномерного случая (для тонких пластин при d,

Для вывода параметров пористости рассмотрим уравнение Лейбензона (8).

Полагая, что в уравнении (8) Р²=Ф(х, y, t), вместо уравнения (8) получаем:

где

Решение уравнения (38) удовлетворяет следующим граничным и начальным условиям:

Ф(х, 0, z, t)=Ф(х, b, z, t)=0,

Ф(0, y, z, t)=Ф(d, y, z, t)=0

Ф(х, y, z, 0)=f(х, y, z), 0<z<l, 0<y<b, 0<x<d.

Вместо уравнения (38) рассмотрим следующее уравнение:

где образец начинаем рассматривать с противоположного торца, т.е. из вакуумированной полости:

Решением уравнения (40), удовлетворяющим условиям (41), является функция:

где

По аналогии с (11) в качестве начального условия возьмем функцию:

Тогда

где n=1, 2, 3...

Следовательно:

Учитывая граничные условия (41), что , получаем:

Введем обозначения:

обусловленное движением воздуха (газа) от границы твердого пористого тела до вакуумированной полости.

Учитывая, что Ф(x, y, z, t)=P²(x, y, z, t), вместо выражения (45) с учетом (46), имеем:

Граничные условия (41) выглядят так:

Для определения давления на входе полости с разреженным газом согласно уравнению Лейбензона предварительно найдем массу газа (воздуха), прошедшую в полость с разреженным газом за время t проведения эксперимента.

Тогда давление на входе полости с разреженным газом равно:

Если d=∞, b=∞, получаем одномерный случай:

Полагая, что , уравнение (51) примет вид:

При выходе на линейный участок в уравнении (52) заменяем Р_и на Р_и-Р_с, т.е.

Для трехмерного случая

при t_и>t_с

где

Рассмотрим связи между параметрами.

Из сравнения левых частей уравнения (26) и (55) получаем:

где

Сравнивая уравнение Дарси с уравнением Фика для стационарного потока, получаем:

Отсюда,

Из уравнения (26) находим коэффициент диффузии:

Тогда коэффициент проницаемости:

Найденное значение К₀ подставляем в (56), получаем коэффициент пористости:

Известно, что

где ν - коэффициент кинематической вязкости, тогда коэффициент фильтрации:

Из равенства (59) имеем коэффициент растворимости газа:

Таким образом, для трехмерной модели истечения газа по порам материала получаем следующие зависимости:

- коэффициент растворимости:

- коэффициент фильтрации:

- коэффициент пористости:

- коэффициент газопроницаемости

- коэффициент диффузии:

где или .

Таким образом, в предлагаемом способе обеспечена возможность исследования трехмерной модели истечения газа через пористые материалы, что позволяет повысить точность способа по сравнению с прототипом на 30-35%.

На чертеже представлена схема устройства для реализации данного способа.

Устройство содержит измерительный стакан 1, в котором расположен шток 2, на одном конце которого закреплен поршень 3, снабженный резиновой прокладкой для герметизации системы, а другой выход штока 2 соединен с пневмоцилиндром большего объема (условно не показан). Устройство герметично соединено с контролируемым материалом 4, образуя измерительную камеру 5. Герметичность соединения обеспечивается за счет деформации прокладок из вакуумной резины 6 под действием усилия Q и манжеты 7. В стенках стакана 1 установлены датчики давления 8, времени 9 и температуры 10. Выходы датчиков давления 8 и времени 9 соединены с входом ЭВМ 11 через электронное согласующее устройство 12. Выход датчика температуры 10 соединен с входом ЭВМ 11. Шток пневмоцилиндра посредством датчика перемещения 13 штока поршня через преобразователь 14 соединен с ЭВМ 11. Измерительная камера 5 посредством электропневмоклапана 15 соединена с насосом (условно не показан). Электропневмоклапан 15 соединен с ЭВМ 11.

Способ осуществляется следующим образом.

Измерительный стакан 1 устанавливается на контролируемый материал 4. Шток 2 с поршнем 3 находятся в крайнем нижнем положении. ЭВМ 11 подает сигнал на открытие электропневмоклапана 15, воздух откачивается из измерительной камеры 5 насосом. После окончания откачивания воздуха ЭВМ 11 закрывает электропневмоклапан 15 и отключает насос, датчик температуры 10 измеряет температуру в измерительной камере 5 и подает информацию на ЭВМ 11. Датчик давления 8 фиксирует остаточное давление газа в измерительной камере 5 и подает информацию о величине давления газа в камере 5 на ЭВМ 11. Если остаточное давление газа больше давления, обеспечивающего молекулярное течение газа через поры, ЭВМ 11 подает команду на перемещение штока 2, которое измеряется датчиком перемещения 13 штока поршня. Поршень 3 поднимается вверх, создавая разрежение воздуха в измерительной камере 5. Как только давление газа в измерительной камере 5 достигнет значения давления, обеспечивающего молекулярное течение газа через материал, датчик давления 8 подаст сигнал на ЭВМ 11, которая отключит перемещение штока 2 пневмоцилиндра. Информация о величине перемещения штока 2 с поршнем 3 с датчика перемещения 13 штока поршня подается на преобразователь 14, который преобразует линейное перемещение поршня 3 в величину объема образовавшейся измерительной камеры 5. Преобразователь 14 подает информацию об объеме измерительной камеры 5 на ЭВМ 11. Датчик давления 8 зафиксирует величину остаточного (начального) давления, датчик температуры 10 зафиксирует значение температуры в измерительной камере 5. Датчик времени 9 начнет отсчет времени процесса течения газа через контролируемый материал 4 в измерительную камеру 5. Давление в измерительной камере 5 будет повышаться за счет течения газа через поры контролируемого материала. Изменение давления с течением времени будет отслеживаться датчиком давления 8 и датчиком времени 9, данные с которых передаются на электронное согласующее устройство 12. Электронное согласующее устройство 12 будет фиксировать каждое последующее приращение давления, соответствующее определенному промежутку времени. Полученный сигнал подается на ЭВМ 11 для сравнения последующего приращения давления в измерительной камере 5 с предыдущим. ЭВМ 11 по специальной программе строит графическую зависимость изменения давления в измерительной камере 5 с течением времени. По графику определяются численные значения давления Р_с, Р_и, времени t_с и t_и (фиксированные промежутки времени), где t_и>t_c, P_и>Р_с.

Данные о площади F материала, ограниченной измерительной камерой, атмосферном давлении Р_а, газовой постоянной R₀, коэффициенте кинематической вязкости ν, коэффициенте динамической вязкости μ, длине l, толщине d и ширине b материала введены в ЭВМ 11 заранее. Поэтому ЭВМ 11 осуществляет определение коэффициента фильтрации из формулы:

коэффициента проницаемости из формулы:

коэффициента диффузии из формулы:

коэффициента растворимости (константа Генри) из формулы:

коэффициент пористости из формулы:

где или .

Способ определения параметров пористости материалов, при котором из герметично соединенной с материалом измерительной камеры откачивают воздух, регистрируют температуру и измеряют величину давления в измерительной камере, отличающийся тем, что после откачивания воздуха увеличивают объем измерительной камеры, осуществляя тем самым разрежение газа до давления, обеспечивающего возможность молекулярного течения газа через поры контролируемого материала, измеряют этот объем измерительной камеры, фиксируют время начала процесса течения газа через материал, остаточное давление газа и температуру в камере в этот период, а коэффициенты фильтрации (К_ф), проницаемости (К₀), диффузии (D), растворимости (константа Генри - К_г) и пористости (П) определяют из соотношений:

коэффициент растворимости:

коэффициент фильтрации:

коэффициент пористости:

коэффициент газопроницаемости:

коэффициент диффузии:

где или

где V_и - объем газа, протекающего в единицу времени t_и при давлении Р_и в измерительную камеру;

F - площадь контролируемого изделия, ограниченная измерительной камерой;

μ - коэффициент динамической вязкости;

P_c, t_c - давление и время в измерительной камере, соответствующие переходу от кнудсеновского к ламинарному режиму течения газа;

Р_и, t_и - текущее значение давления и времени, t_и>t_с;

P_a - атмосферное давление;

ν - коэффициент кинематической вязкости;

l - длина контролируемого материала;

b - ширина материала, ограниченная измерительной камерой;

d - толщина материала, ограниченная измерительной камерой.