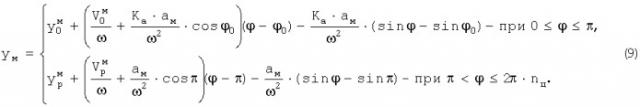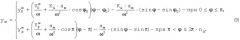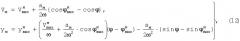Способ формирования спиралевидного движения планирующего летательного аппарата относительно опорной траектории

Способ формирования спиралевидного движения планирующего летательного аппарата относительно опорной траектории

Иллюстрации

Показать все

Реферат

Изобретение относится к управлению летательных аппаратов (ЛА) и может быть использовано для решения задач маневрирования, при этом не отклоняясь от опорной траектории. Этот способ реализует маневр типа пространственная бочка (далее для краткости «спираль»), при котором ЛА создает в вертикальной и горизонтальной плоскостях ускорения, меняющиеся по гармоническому закону и сдвинутые друг относительно друга на 90 градусов.

Известен способ формирования маневра [1], согласно которому ЛА на околозвуковой скорости способны выполнять «спираль» с перегрузками 5-6 единиц и периодом порядка 4 с, и более интенсивно - беспилотные ЛА, например противорадиолокационные ракеты, при числе Маха три выполняют «спираль» с перегрузками до 20 единиц и периодом 2...3 с.

Недостатком наиболее близкого по своей сущности способа формирования маневра является то, что его осуществление приводит к невыходу на опорную траекторию ЛА при прекращении маневрирования.

Требуемый технический результат - способ формирования маневра с заданными алгоритмом и периодом и возвращением на опорную траекторию при прекращении маневрирования.

Требуемый технический результат достигается осуществлением маневра за счет трехэтапных синусоидальных силовых воздействий на аппарат в вертикальной и горизонтальной плоскостях, причем на каждом из трех этапов задается свое значение коэффициента передачи управляющего воздействия. Значения коэффициентов передачи для каждого из этапов являются особенностью данного изобретения.

На Фигуре 1 представлена циклограмма формирования маневра типа змейка в вертикальном и горизонтальном каналах. На Фигуре 2 для произвольного варианта исходных данных изображен маневр «спираль» в поле скоростей и координат.

Рассмотрим модельную задачу, позволяющую выявить основные параметры маневра «спираль» и требуемый закон изменения управляющих сил. Пусть ЛА, схематизируемый материальной точкой постоянной массы, движется прямолинейно и равномерно. Управление движением по нормали к начальному направлению вектора скорости выполняется целенаправленно изменяемой подъемной силой, определяемой управляющими параметрами - пространственным углом атаки и углом скоростного крена. Пространственный угол атаки ограничен по модулю.

Рассмотрим плоский случай маневра, то есть маневр «змейка». Известно [2], что материальная точка, находившаяся в состоянии покоя или равномерного прямолинейного движения, под действием гармонической силы с постоянной амплитудой приобретает дополнительную скорость, состоящую из постоянной и синусоидальной составляющих. При соответствующем выборе момента прекращения действия силы синусоидальная составляющая обращается в ноль, а постоянная сохраняется на прежнем уровне.

Проанализируем возможности устранения и постоянной составляющей скорости маневра, для чего запишем динамическое уравнение маневрирования ЛА в виде:

где - скорость маневра ЛА по нормали к направлению первоначального движения,

ω - круговая частота маневра,

а_м - нормальное ускорение для формирования маневра,

К_а - коэффициент передачи ускорения из диапазона [0...1] на участках входа

и выхода из маневра, 1 - на участке маневра.

Примем схему маневра, состоящую из трех участков, на которых независимая переменная ϕ=ωt изменяется в диапазонах:

где n_ц - количество циклов маневра (n_ц≥1).

Из (1) следует:

откуда

где , - скорость V_м в начале маневрирования и при ϕ=π.

Скорость маневра на интервале π<ϕ≤2π·n_ц, вычисленная в силу (4) при , содержит постоянную и синусоидальную составляющие:

Для устранения постоянной составляющей скорости следует положить на участке входа, то есть при 0≤ϕ≤π:

Теперь с учетом найденной величины К_а выражение (4) принимает вид:

Координата у_м маневра «змейка» определяется из уравнения:

откуда с учетом (4):

Определив в силу (9) при величину и в силу (7) величину

запишем:

Рассмотрим участок выхода из маневра «змейка». Проверим предположение, что выход, как и вход, выполняется при К_а=1/2, но на интервале

где

В соответствии с (4) и (9) запишем:

где - скорость и координата маневра в момент начала выхода.

После преобразований (12) с учетом (7) и (10) получим:

Проверка показывает, что выражения (13) отвечают требуемым краевым условиям на левой и правой границах участка выхода из маневра:

и, следовательно, сделанное выше предположение о величине К_а при выходе из маневра верно.

Итак, проведенные выкладки показывают, что маневр «змейка» ЛА из состояния прямолинейного движения с возвращением на ту же траекторию после завершения маневра должен состоять из участков входа в маневр, маневра и выхода из маневра. Причем на участках входа и выхода движение должно выполняться с половинным уровнем нормального ускорения, действующего на участке маневра.

Представим в табл.1 выражения фазовых координат маневра в более удобной форме, для чего рассмотрим выражение (10):

из которого следует, что амплитуда синусоидальной составляющей маневра относительно его среднего положения есть

В связи с тем, что величина нормального ускорения а_м ограничена, справедливо неравенство, связывающее амплитуду маневра, его круговую частоту и максимальное значение а_мах нормального ускорения:

Теперь рассмотрим пространственный маневр ЛА, то есть маневр «спираль», реализуемый плоскими «змейками» в горизонтальной и в вертикальной плоскостях. Причем установим, что вертикальная «змейка» отстает от горизонтальной на угол π/2. Кроме того, для возможности задания «спирали» эллипсоидальной формы нормальные ускорения в указанных плоскостях зададим различными, что приведет к различию амплитуд вертикальной и горизонтальной «змеек»:

где М_y,z - коэффициенты формы «спирали» (0≤М_y,z≤1).

Динамические уравнения «змеек» по обоим каналам аналогичны (1) и с учетом запаздывания «змейки» в вертикальном канале на π/2 принимают вид:

где - коэффициенты передачи ускорения на участках маневра «спираль».

Из фиг.1 которой следует, что выделяются семь интервалов задания коэффициентов

В табл.2 для каждого из семи интервалов приведены требуемые коэффициенты передачи ускорений и теоретические значения кинематических параметров маневра «спираль», формируемого относительно исходной траектории, в соответствии с аналитическими выражениями табл.2 построена фиг.2.

Итак, придавая ЛА дополнительное кажущееся ускорение, определяемое выражениями (19), и одновременно продолжая управление ЛА в соответствии с заданным маршрутом, реализуем пространственный маневр типа «спираль», что позволяет сохранить опорную траекторию ЛА в соответствии с требуемым техническим результатом.

Источники информации

1. Проектирование зенитных управляемых ракет: Учебник / И.И.Архангельский, П.П.Афанасьев, Е.Г.Болотов и др. Под ред. И.С.Голубева и В.Г.Светлова. М.: Изд-во МАИ, 1999, 728 с.

2. Основы физики: Учеб. для вузов: В 2 т. / Н.П.Калашников, М.А.Смондырев. - 2-е изд., перераб. - М.: Дрофа, 2003, т.1, 400 с.

Способ формирования планирующего спиралевидного движения летательного аппарата относительно опорной траектории, включающий трехэтапные синусоидальные силовые воздействия на аппарат в вертикальной и горизонтальной плоскостях с различием по фазе на π/2, отличающийся тем, что на каждом этапе задается свое значение коэффициента передачи управляющего воздействия, при входе в маневр - 1/2, в процессе маневра - 1, при выходе из маневра - 1/2.