Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе

Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе

Иллюстрации

Показать все

Реферат

Изобретение относится к технике управления летательными аппаратами и может применяться для наведения летательных аппаратов на воздушные цели с использованием угломерных двухпозиционных радиолокационных систем (УДПРЛС).

Наблюдение за целями, на которых размещены источники радиоизлучений (ИРИ), может осуществляться на основе приема сигналов, излучаемых их радиоэлектронными средствами, с помощью угломерных двухпозиционных радиолокационных систем [Меркулов В.И., Харьков В.П., Чернов B.C. Алгоритмы управления позициями в пассивной двухпозиционной РЛС. «Радиотехника», 2004, №10, стр.86-90].

Эффективность применения УДПРЛС во многом зависит от способа управления летательными аппаратами (ЛА), на которых размещаются приемные позиции этой системы, поскольку в процессе управления изменяется взаимное положение летательных аппаратов и ИРИ, в значительной степени влияющее на точность определения местоположения радиоизлучающих целей [Дрогалин В.В., Ефимов В.А., Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. «Успехи современной радиоэлектроники. Зарубежная радиоэлектроника», 2003, №5, стр.22-38].

При применении угломерных двухпозиционных радиолокационных систем, как правило, необходимо одновременно решать две задачи, а именно: задачу наведения летательных аппаратов на воздушную радиоизлучающую цель и задачу траекторного управления летательными аппаратами для создания наиболее благоприятных условий для высококачественного радиолокационного наблюдения за радиоизлучающей целью. В связи с этим разрабатываются способы, предусматривающие решение задачи управления процессом наблюдения с одновременным наведением на ИРИ. При этом наиболее трудоемкой является организация управления летательными аппаратами в горизонтальной плоскости.

Известен способ управления движением двух самолетов по курсу в горизонтальной плоскости [Меркулов В.И., Харьков В.П., Чернов B.C. Алгоритмы управления позициями в пассивной двухпозиционной РЛС. «Радиотехника», 2004, №10, стр.86-90], согласно которому наводящийся на ИРИ самолет, называемый в дальнейшем для краткости ударным самолетом, управляется в соответствии с одним из существующих способов самонаведения, а второй самолет - самолет информационного обеспечения выводится на прямую, ортогональную линии визирования ударный самолет - ИРИ и проходящую через ИРИ, где существуют наилучшие условия для радиолокационного наблюдения за ИРИ. При этом задача синтеза желаемого управления для самолета обеспечения решена на основе математического аппарата теории обратных задач динамики.

Основным недостатком данного способа является то, что не фиксируется точка, в районе которой должен оказаться самолет информационного обеспечения при выводе на прямую, ортогональную линии визирования ударный самолет - ИРИ. В результате не гарантируется безопасность самолета информационного обеспечения и не контролируется время его выхода в указанную точку. Кроме того, недостатком данного способа является высокая сложность информационно-вычислительных систем самолетов с пеленгаторами, большой объем информации, которой должны обмениваться самолеты, а также наличие ограничений на условия применения [Меркулов В.И., Харьков В.П., Чернов B.C. Алгоритмы управления позициями в пассивной двухпозиционной РЛС. «Радиотехника», 2004, №10, стр.90].

Аналогичные недостатки характерны также для способа наведения летательных аппаратов на источник радиоизлучения в двухпозиционной радиолокационной системе, описанного в патенте РФ №2262649.

Указанные недостатки устранены в способе управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе (Патент РФ №2256870), выбранном в качестве прототипа заявленного изобретения. Согласно этому способу ЛА информационного обеспечения, называемый для краткости вторым ЛА, наводится по кривой погони в наилучшую точку наблюдения (НТН), находящуюся на перпендикуляре к линии ударный ЛА - ИРИ на удалении от ИРИ, равном расстоянию ИРИ от ударного ЛА, условно считающегося первым ЛА. Данный способ предусматривает совмещение продольной оси второго ЛА в процессе наведения с направлением на НТН. Положение НТН в пространстве непрерывно изменяется за счет сближения первого ЛА и ИРИ. Поэтому предусмотренная данным способом процедура наведения в НТН по кривой погони в определенных тактических ситуациях может потребовать от второго ЛА выполнения разворота с поперечными перегрузками, лежащими вне допустимого диапазона. Кроме того, при реализации данного способа не всегда обеспечивается плавный выход второго ЛА на линию ИРИ - НТН.

Отмеченные недостатки, имеющие место в процессе наведения второго ЛА, приводят к снижению эффективности применения УДПРЛС. Поэтому задача настоящего изобретения состоит в разработке способа управления ЛА по курсу в угломерной двухпозиционной радиолокационной системе, обеспечивающего наведение ударного ЛА на ИРИ и создание летательным аппаратом информационного обеспечения благоприятных условий для проведения радиолокационных наблюдений за радиоизлучающей целью, в максимальной степени свободного от недостатков прототипа.

Поставленная задача достигается тем, что в способе управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе, заключающемся в том, что измеряют значения пеленгов источника радиоизлучений (ИРИ) соответственно на первом и втором летательных аппаратах (ЛА), измеряют координаты первого и второго ЛА в прямоугольной системе координат и их курсы, между первым и вторым ЛА осуществляют взаимный обмен результатами измерений пеленгов ИРИ, прямоугольных координат ЛА и их курсов, на каждом ЛА оценивают координаты ИРИ в прямоугольной системе координат и расстояния до ИРИ от соответствующих ЛА, выбирают ЛА, обеспечивающий минимальное время полета ЛА к ИРИ, и осуществляют самонаведение выбранного ЛА на ИРИ, согласно изобретению дополнительно измеряют скорость второго ЛА, на втором ЛА оценивают азимуты ИРИ относительно первого и второго ЛА, угловую скорость ω₁, линии визирования ИРИ - первый ЛА, угловую скорость ω₂ линии визирования ИРИ - второй ЛА, находят прямоугольные координаты и скорости их изменения для наилучшей точки наблюдения (НТН), а также скорость перемещения и курсовой угол НТН, определяют азимут β_н ИРИ относительно НТН, азимут β_2Н НТН относительно второго ЛА, расстояние R_2Н до НТН от второго ЛА, с учетом измеренной скорости второго ЛА определяют требуемый угол упреждения q_y второго ЛА и формируют параметр управления Δ₂ вторым ЛА согласно соотношению:

где:

ψ₂ - курс второго ЛА;

ω_н - угловая скорость линии ИРИ - НТН, при этом ω_н=ω₁;

к_ψ, к_β, к_ω - весовые коэффициенты ошибок наведения второго ЛА по курсу, азимуту и угловой скорости линии визирования соответственно;

к_у - весовой коэффициент угла упреждения;

R_раз. - расстояние до НТН от второго ЛА, при достижении которого изменяют алгоритм траекторного управления;

отклоняют органы управления вторым ЛА по курсу и при выходе второго ЛА на линию ИРИ - НТН устанавливают скорость полета второго ЛА равной скорости перемещения НТН.

Благодаря дополнительному, по сравнению с прототипом, измерению скорости второго ЛА, оцениванию параметров собственного движения наилучшей точки наблюдения и параметров относительного движения НТН и ИРИ, а также введению в параметр управления вторым ЛА новых составляющих обеспечивается плавный выход второго ЛА на перпендикуляр к линии первый ЛА - ИРИ и совмещение его с наилучшей точкой наблюдения.

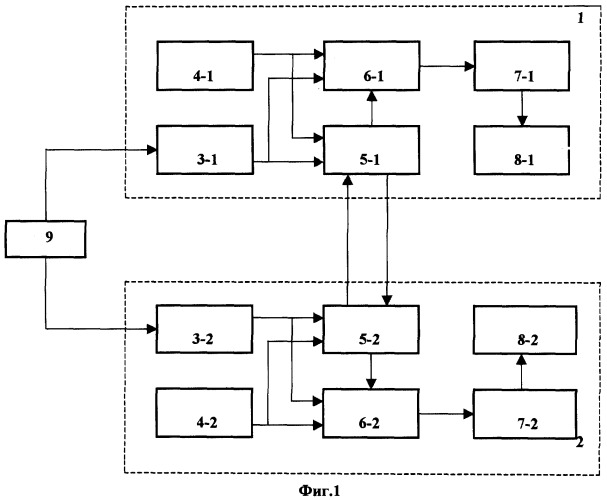
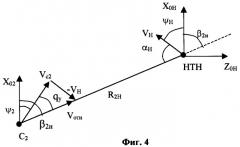
На фиг.1 представлена упрощенная структурная схема возможного варианта УДПРЛС, реализующей предлагаемый способ, где 1, 2 - первая и вторая приемные позиции соответственно; 3-1, 3-2 - угломеры, 4-1, 4-2 - навигационные системы; 5-1, 5-2 - аппаратура передачи данных; 6-1, 6-2 - вычислительные системы; 7-1, 7-2 - системы автоматического управления; 8-1, 8-2 - летательные аппараты (ЛА), 9 - цель (ИРИ). Фиг.2 поясняет обозначения, входящие в формулу для ошибки определения местоположения цели, в качестве которой выступает ИРИ. Фиг.3 иллюстрирует геометрию наведения летательных аппаратов в горизонтальной плоскости и поясняет величины, входящие в формулу для параметра управления вторым ЛА в УДПРЛС. Фиг.4 поясняет обозначения, входящие в формулу для оценки угла упреждения. На фиг.5-7 приведены результаты моделирования процесса наведения двух ЛА.

Рассмотрим возможный вариант функционирования УДПРЛС при использовании заявленного способа управления летательными аппаратами по курсу (фиг.1).

Приемные позиции 1, 2 являются подвижными и размещаются соответственно на первом и втором ЛА 8-1, 8-2. Каждая приемная позиция 1 (2) содержит одинаковый состав оборудования: угломер РЛС 3-1 (3-2), навигационную систему 4-1 (4-2), аппаратуру передачи данных 5-1 (5-2) и вычислительную систему 6-1 (6-2).

На фиг.2 и 3 первый ЛА 8-1 обозначен точками C₁, второй ЛА 8-2 - точками С₂, цель (ИРИ) 9 - точками Ц. Заявленный способ обеспечивает оценивание координат цели 9 (ИРИ) х_ц, z_ц в горизонтальной плоскости, азимутов цели β₁, и β₂ относительно двух ЛА и угловых скоростей ω₁, и ω₂ линий визирования, соединяющих ЛА и ИРИ, соответственно расстояний до ИРИ от ЛА R₁ и R₂ (фиг.3). Вектор первичных наблюдаемых параметров включает пеленги ИРИ ϕ₁, и ϕ₂ в точках пеленгации, совпадающих с местами нахождения первого и второго ЛА 8-1, 8-2, соответственно, C₁ и С₂, а также прямоугольные координаты x_c1, z_c1 и x_с2, z_c2, скорости V₁ и V₂ и курсы ψ₁, ψ₂ первого и второго ЛА 8-1, 8-2 (точки C₁ и С₂).

ИРИ, пространственно совпадающий с целью 9, формирует радиосигналы, принимаемые в первой и второй приемных позициях 1, 2. Источниками радиоизлучения могут быть станция активных помех либо РЛС, установленные на цели. Угломеры 3-1, 3-2, называемые также пеленгаторами, измеряют пеленги ИРИ ϕ₁ и ϕ₂ в каждой приемной позиции 1, 2. Навигационные системы 4-1 и 4-2 определяют местоположение летательных аппаратов 8-1, 8-1 x_c1, z_c1 и x_с2, z_c2 в прямоугольной системе координат, их скорости V₁ и V₂ и курсы ψ₁, ψ₂. Предпочтительным вариантом для определения координат ЛА является использование спутниковой радионавигационной системы как наиболее точной. Измеренные значения пеленгов ИРИ, прямоугольных координат и курсов ЛА с помощью аппаратуры передачи данных 5-1 и 5-2 передаются с одной позиции на другую. В вычислительные системы 6-1 и 6-2 поступают результаты измерения пеленгов ИРИ в двух позициях, прямоугольных координат, скоростей и курсов ЛА.

В вычислительных системах происходит формирование оценок координат ИРИ х_ц, z_ц а также азимутов ИРИ β₁ и β₂, угловых скоростей ω₁ и ω₂ линий визирования и расстояний до ИРИ от ЛА 8-1 и 8-2 R₁ и R₂ соответственно, процедура получения которых подробно описана в [Дрогалин В.В., Ефимов В.А., Канащенков А.И. и др. Алгоритмы оценивания координат и параметров радиоизлучающих целей в угломерных двухпозиционных бортовых радиолокационных системах. «Информационно-измерительные и управляющие системы», 2003, т.1, №1, стр.4-22].

На основе заложенных в вычислительные системы критериев назначения летательных аппаратов выбирается первый ЛА для атаки воздушной цели и второй ЛА, который обеспечивает наилучшие условия радиолокационных наблюдений радиоизлучающей цели. В вычислительных системах вырабатываются параметры управления летательными аппаратами в зависимости от задач, возлагаемых на конкретный ЛА. Управление вторым ЛА заключается в наведении его в наилучшую точку наблюдения. Местонахождение этой точки определяется на основе следующих соображений.

Ошибки измерителей приводят к погрешностям формирования (расчета) оценок координат x_ц и z_ц. Анализ точности определения местоположения ИРИ при функционировании УДПРЛС, проведенный в [Дрогалин В.В., Ефимов В.А, Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. «Успехи современной радиоэлектроники. Зарубежная радиоэлектроника», 2003, №5, стр.25-38], показал, что ошибки определения местоположения ИРИ зависят от «геометрии» системы, т.е. от размеров базы и положения ИРИ относительно базы, а также от погрешностей измерения пеленгов, прямоугольных координат и курсов ЛА. Под базой понимается линия, соединяющая первый и второй ЛА. Из анализа следует важный вывод о том, что существуют определенные условия, наиболее благоприятные для проведения радиолокационных наблюдений в УДПРЛС, при выполнении которых минимизируются ошибки определения местоположения ИРИ. Как известно, ошибки пеленгации ИРИ могут быть постоянными и случайными.

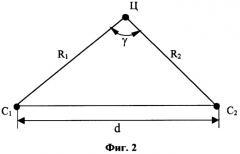
Точность определения местоположения радиоизлучающих целей при постоянных ошибках пеленгации характеризуется наибольшей линейной ошибкой. Линейная погрешность достигает минимума для точек, лежащих на окружности, радиус которой равен половине базы. В этом случае линии пеленгов пересекаются под прямым углом (фиг.2).

На фиг.2 введены следующие обозначения: R₁ и R₂ - расстояния от источника радиоизлучения (точка Ц) до ЛА C₁ и C₂, оборудованных пеленгаторами; γ - угол пересечения линий визирования; d - база пеленгации.

При случайных ошибках пеленгации и при использовании в качестве показателя точности средней квадратичной ошибки местоопределения σ_r, в случае одинаковых ошибок пеленгаторов σ_α1=σ_α2=σ_α имеет место соотношение [Дрогалин В.В., Ефимов В.А., Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой. «Успехи современной радиоэлектроники. Зарубежная радиоэлектроника», 2003, №5, стр.32]

Смысл переменных, входящих в это уравнение, поясняется фиг.2.

Ошибка σ_r зависит от значений γ, R₁ и R₂. Из формулы (3) видно, что точность измерения наиболее высока, если угол γ пересечения линий положения достаточно близок к прямому углу, и заметно снижается, если линии положения пересекаются под острым углом. Минимизация ошибки местоопределения σ_r при заданных значениях расстояний R₁ и R₂ достигается выбором размера базы, при котором угол γ=90°.

Таким образом, минимальная ошибка местоопределения получается при определенной «геометрии» системы. Для любого заданного расстояния R₁ оптимальное положение второго пеленгатора лежит на перпендикуляре к направлению первого пеленга, проходящем через объект пеленгации.

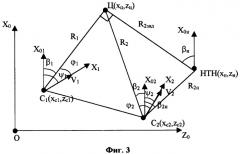
При применении пары ЛА с использованием УДПРЛС выбор ударного ЛА определяется заданным критерием. В качестве критерия назначения ЛА для атаки, как правило, выбирают минимум расстояния от ЛА до цели. Тогда для геометрии взаимного положения летательных аппаратов и цели, показанной на фиг.3, таким ЛА будет ЛА C₁, у которого R₁<R₂. На фиг.3 точки C₁, C₂ и Ц соответствуют проекциям центров масс ЛА и ИРИ на горизонтальную плоскость. X₀OZ₀ - неподвижная прямоугольная система координат, в которой осуществляется решение задачи наведения ЛА. Оси C₁X₀₁, C₂Х₀₂ параллельны оси ОХ₀. Относительно этих осей отсчитываются азимуты и курсы. При нулевых углах скольжения проекции V₁ и V₂ векторов скоростей ЛА на горизонтальную плоскость совпадают с проекциями C₁X₁, C₂Х₂ продольных осей ЛА C₁, C₂ на эту же плоскость. Положение ИРИ относительно точки C₁ характеризуется полярными координатами R₁ и β₁. Управление первым ЛА C₁ при наведении на воздушную цель может выполняться на основе любого из известных способов самонаведения [Авиационные системы радиоуправления. Т.2. Радиоэлектронные следящие системы. / Под ред. А.И.Канащенкова, В.И.Меркулова. - М.: Радиотехника, 2003, стр.15-23], например, путем наведения в наивыгоднейшую упрежденную точку встречи либо способом прямого наведения.

Пусть второй ЛА C₂ решает задачу обеспечения наилучших условий радиолокационного наблюдения (фиг.3). Поскольку ориентация вектора дальности R₁ и его длина определяются процедурой наведения ЛА C₁ на цель, то управление наблюдением может осуществляться только за счет изменения положения ЛА C₂.

С учетом обеспечения безопасности второго ЛА C₂ наименьшая ошибка оценивания местоположения ИРИ соответствует случаю, когда линии визирования ИРИ с двух точек пеленгации пересекаются под прямым углом γ=90°, а расстояние R₂=R_2зад, где R_2зад - заданное расстояние до ИРИ от наилучшей точки наблюдения, большее или равное расстоянию до ИРИ от первого ЛА C₁. Такой геометрии взаимного расположения приемных позиций и ИРИ соответствует точка НТН (фиг.3) требуемого нахождения второго ЛА С₂. Условно данную точку будем называть наилучшей точкой наблюдения (НТН) с заданной дальностью до цели. Отметим, что положение НТН непрерывно изменяется в пространстве, так как цель движется и изменяется угловое положение линии визирования первый ЛА - ИРИ (C₁-Ц) и дальность до ИРИ R₁.

При известном азимуте ИРИ β₁ в точке C₁ азимут ИРИ относительно наилучшей точки наблюдения β_н=β₁+270°, а угловая скорость линии Ц - НТН равна угловой скорости линии визирования Ц - C₁: . В идеальном случае второй ЛА C₂ должен находиться в НТН. Для выхода в НТН параметр управления вторым ЛА С₂ в заявленном способе рассчитывается по формуле (1) до момента достижения дальности до НТН, равной R_раз..

Для нахождения требуемого курса полета второго ЛА С₂ необходимо знать прямоугольные координаты x_н, z_н наилучшей точки наблюдения и x_с2, z_c2 второго ЛА С₂. При наведении в НТН способом прямого наведения требуемый курс второго ЛА C₂, равный азимуту НТН относительно второго ЛА С₂, рассчитывается по формуле (фиг.3)

Наличие двух формул для вычисления значений требуемого курса объясняется тем, что курс ЛА может иметь только положительное значение и изменяться в диапазоне от 0 до 360°.

Координаты второго ЛА С₂ оцениваются в результате проведения навигационных измерений, а координаты НТН вычисляются из условия достижения наилучших результатов наблюдения на основе полученных оценок прямоугольных координат ИРИ и заданного положения НТН относительно ИРИ. Для нахождения прямоугольных координат НТН к оцененным координатам ИРИ добавляют прямоугольные проекции вектора R_2зад, соединяющего ИРИ с НТН. Расчетные формулы для прямоугольных координат НТН следуют из фиг.3.:

β₁=ψ₁-ϕ₁

где ψ₁ - курс первого ЛА C₁;

ϕ₁ - пеленг ИРИ в точке нахождения первого ЛА C₁.

Расстояние до наилучшей точки наблюдения от второго ЛА R_2н определяется на основе соотношения (фиг.3):

Аналогично рассчитываются расстояния до ИРИ от первого и второго ЛА C₁ и С₂:

Наведение по прямому способу приводит к существенному искривлению траектории движения второго ЛА. Поэтому при наведении второго ЛА приходится использовать более сложные способы наведения, что достигается за счет использования в той или иной форме углового упреждения. Методика выбора углов упреждения известна [Авиационные системы радиоуправления. Т.2. Радиоэлектронные следящие системы. / Под ред. А.И.Канащенкова, В.И.Меркулова. - М.: Радиотехника, 2003, стр.12-22]. При реализации заявленного способа выражение для угла упреждения получается наиболее простым при использовании алгоритма траекторного управления, относящегося к способу параллельного сближения [Дудник П.И., Чересов Ю.И. Авиационные радиолокационные устройства. - М.: ВВИА имени проф. Н.Е.Жуковского, 1986, стр.365]. Применительно к принятым обозначениям, смысл которых поясняется фиг.4, выражение для угла упреждения имеет вид:

где - скорость перемещения НТН;

- составляющие скорости V_н по осям прямоугольной системы координат;

V₂ - скорость второго ЛА С₂;

α_н=π-(β_2н-ψ_н) - угол между вектором скорости V_н и линией визирования С₂ - НТН;

- курсовой угол перемещения НТН.

При выводе формулы (6) использовано условие, что вектор относительной скорости V_отн при способе параллельного сближения должен быть направлен на НТН.

Кратко охарактеризуем закон формирования параметра управления вторым ЛА, описываемый выражениями (1) и (2). Параметр управления (1) обеспечивает наведение второго ЛА в НТН, лежащую на перпендикуляре к линии визирования ИРИ - первый ЛА. Параметр управления (1) при выборе 0<к_у<1 соответствует прямому способу наведения со смещением. Выбором весового коэффициента к_ψ добиваются уменьшения влияния ошибок определения местоположения НТН на процедуру формирования параметра управления вторым ЛА, а подбором весового коэффициента к_у уменьшают кривизну траектории, присущей прямому способу наведения.

Использование параметра управления в виде (1) может приводить к ситуациям, когда на конечном участке наведения второй ЛА будет пересекать линию ИРИ - НТН, не выходя при этом на указанную линию. Это означает, что траектория второго ЛА после выхода его в НТН не будет совпадать с линией ИРИ - НТН. Для предотвращения подобных явлений при подлете второго ЛА к НТН на расстояние R_2н=R_раз параметр управления начинают рассчитывать по соотношению (2). При этом в формулах (4) и (5) R_2зад уменьшается на величину R_раз. Расстояние R_раз выбирают равным радиусу виража второго ЛА при заданном значении перегрузки и рассчитывают по формуле [Дудник П.И., Чересов Ю.И. Авиационные радиолокационные устройства. - М.: ВВИА имени проф. Н.Е.Жуковского, 1986, стр.364]

где g - ускорение силы тяжести; n_зад - заданная перегрузка.

Под действием второго и третьего слагаемых параметра управления (2) второй ЛА на конечном участке сближения дополнительно разворачивается и плавно выходит на линию ИРИ - НТН. Так как азимуты ИРИ и угловые скорости линий визирования оцениваются с высокой точностью, то при соответствующем выборе весовых коэффициентов второй ЛА выводится на линию ИРИ - НТН с малыми ошибками.

Параметр управления (1), (2) используют для изменения направления движения второго ЛА в горизонтальной плоскости. Для этого параметр управления подают в канал бокового управления системы автоматического управления второго ЛА, где он суммируется с сигналами, обеспечивающими повышение устойчивости и стабилизацию углового положения ЛА в пространстве. Процедура преобразования параметра управления в отклонение рулевых органов является стандартной и приведена, например, в книге [Авиационные системы радиоуправления. Т.2. Радиоэлектронные следящие системы. / Под ред. А.И.Канащенкова, В.И.Меркулова. - М.: Радиотехника, 2003, стр.337-339].

При выходе второго ЛА на линию ИРИ - НТН скорость второго ЛА уменьшают и устанавливают равной скорости перемещения наилучшей точки наблюдения. В противном случае второй ЛА обгонит наилучшую точку наблюдения. Момент выхода второго ЛА на линию ИРИ - НТН определяется временем наступления равенства азимутов β_н и β₂. Азимут ИРИ относительно НТН находят из соотношения (фиг.3):

Для проверки правильности функционирования алгоритмов траекторного управления (1) и (2) было проведено математическое моделирование на ЭВМ процесса наведения летательных аппаратов.

На фиг.5 приведены траектории движения первого и второго ЛА, ИРИ и НТН в горизонтальной плоскости. В начальный момент времени первый и второй ЛА находятся в точках с координатами x_c1(0)=0 км, z_c1(0)=0 км и x_с2(0)=-50 км, z_c2(0)=200 км соответственно, а ИРИ - в точке с координатами x_ц(0)=100 км, z_ц(0)=125 км. Расстояние R_раз. выбрано равным 5 км, коэффициенты к_ψ=10, к_β=1, к_ω=1, к_у=0,5, скорости V₁=200 м/с, V₂=300 м/с, V_ц=100 м/с. Крайняя траектория справа на фиг.5 соответствует движению НТН. ИРИ движется под углом к оси ОХ₀, одновременно удаляясь от оси абсцисс OZ₀. На начальном и среднем участках траектории второй ЛА летит в упрежденную точку встречи с НТН. На конечном участке траектории за 5 км до НТН происходит доворот второго ЛА с выходом на перпендикуляр к линии визирования первый ЛА - ИРИ, т.е. на линию наилучшего наблюдения ИРИ.

На фиг.6 показан график, иллюстрирующий эволюцию ошибки σ_r определения местоположения ИРИ во времени. По оси ординат отложены значения ошибок σ_r в метрах, а по оси абсцисс - дискретное время с шагом 1 с. Решение задачи наведения при моделировании останавливалось после выхода второго ЛА на линию наилучшего наблюдения. Из графика видно, что по мере сближения второго ЛА с НТН ошибка σ_r уменьшается.

На фиг.7 приведен график изменения угла γ в процессе наведения. При выходе второго ЛА на указанный выше перпендикуляр угол γ становится равным 90°, как это и требуется по условиям наведения. На фиг.7 по оси абсцисс отложены значения дискретного времени с шагом 1 с.

Результаты моделирования свидетельствуют о возможности существенного уменьшения ошибок определения местоположения ИРИ, что приводит к повышению эффективности применения УДПРЛС.

Таким образом, заявленный способ в отличие от прототипа позволяет наводить второй ЛА в заданную точку с одновременным разворотом на конечном участке сближения и плавным выходом на линию, обеспечивающую наилучшие условия для радиолокационного наблюдения ИРИ. Достоинством предложенного способа является также снятие ограничений на тактические ситуации, присущие прототипу.

Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе, заключающийся в том, что измеряют значения пеленгов источника радиоизлучений (ИРИ) соответственно на первом и втором летательных аппаратах (ЛА), измеряют координаты первого и второго ЛА в прямоугольной системе координат и их курсы, между первым и вторым ЛА осуществляют взаимный обмен результатами измерений пеленгов ИРИ, прямоугольных координат ЛА и их курсов, на каждом ЛА оценивают координаты ИРИ в прямоугольной системе координат и расстояния до ИРИ от соответствующих ЛА, выбирают ЛА, обеспечивающий минимальное время полета ЛА к ИРИ, и осуществляют самонаведение выбранного ЛА на ИРИ, отличающийся тем, что дополнительно измеряют скорость второго ЛА, на втором ЛА оценивают азимуты ИРИ относительно первого и второго ЛА, угловую скорость ω₁ линии визирования ИРИ - первый ЛА, угловую скорость ω₂ линии визирования ИРИ - второй ЛА, находят прямоугольные координаты и скорости их изменения для наилучшей точки наблюдения (НТН), а также скорость перемещения и курсовой угол НТН, определяют азимут β_н ИРИ относительно НТН, азимут β_2Н НТН относительно второго ЛА, расстояние R_2Н до НТН от второго ЛА, с учетом измеренной скорости второго ЛА определяют требуемый угол упреждения q_у второго ЛА и формируют параметр управления Δ₂ вторым ЛА согласно соотношению:

где

ψ₂ - курс второго ЛА;

ω_н - угловая скорость линии ИРИ-НТН, при этом ω_н=ω₁;

к_ψ, к_β, к_ω - весовые коэффициенты ошибок наведения второго ЛА по курсу, азимуту и угловой скорости линии визирования соответственно;

к_у - весовой коэффициент угла упреждения;

R_раз - расстояние до НТН от второго ЛА, при достижении которого изменяют алгоритм траекторного управления;

отклоняют органы управления вторым ЛА по курсу и при выходе второго ЛА на линию ИРИ-НТН устанавливают скорость полета второго ЛА, равной скорости перемещения НТН.