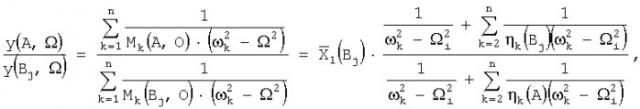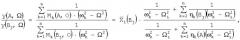Способ определения собственных форм колебаний упругой конструкции

Способ определения собственных форм колебаний упругой конструкции

Иллюстрации

Показать все

Реферат

Изобретение относится к экспериментальным методам определения характеристик собственных колебаний машиностроительных конструкций и может найти применение в различных отраслях машиностроения.

Основными характеристиками собственных колебаний конструкции (модальными параметрами) являются собственные частоты колебаний, собственные формы колебаний и коэффициенты демпфирования. Через модальные параметры записывается решение задачи о колебаниях упругой конструкции под действием произвольной возмущающей силы. Собственные формы колебаний тесно связаны с эквивалентными массами конструкции: зная собственные формы колебаний конструкции, можно определить ее эквивалентные массы, а зная эквивалентные массы конструкции, соответствующие различным точкам, можно определить собственные формы колебаний. В случае упругих тел величины М_k определяются формулой

где ρ - плотность материала, Х_K(А), Х_K(O)- амплитуды колебаний точки наблюдения А и точки возбуждения О при колебаниях конструкции по k-той собственной форме (т.е. значения амплитудных функций в точках А и О), интегрирование производится по объему тела V в случае трехмерных тел, по площади тела - в случае двумерных тел (пластины, оболочки), по длине тела - в случае одномерных тел (стержни). Величины m_K в работе [1] названы обобщенными массами, в работе [Генкин М.Д., Тарханов Г.В. Вибрация машиностроительных конструкций. - М.: Машиностроение, 1979, с.38.] - эквивалентными массами (но не отнесенными к точкам наблюдения и возбуждения).

Собственные формы колебаний упругого тела определяются с точностью до постоянного множителя. Это означает, что если Х_K - амплитудная функция, определяющая его собственную форму колебаний, соответствующую собственной частоте ω_k, то α·Х_k - также является амплитудной функцией (а - любая константа). При определении амплитудной функции можно условно принять, что значение этой функции в некоторой точке А конструкции равно единице. Тогда если конструкция совершает колебания по k-той собственной форме, то значение этой функции в произвольной точке В определяется по формуле

где Х_k(А), Х_k(B) - амплитуды колебаний точек А и В.

Если известны эквивалентные массы конструкции, соответствующие k-той собственной частоте колебаний ω_k двум точкам наблюдения А и В и точке возбуждения О, то значение k-той амплитудной функции в точке В можно определить по формуле (значение рассматриваемой функции в точке А принято за единицу)

Формула (2) показывает, что любой способ определения эквивалентных масс конструкции, соответствующих данной точке возбуждения и точке наблюдения, можно использовать для определения собственных форм колебаний конструкции.

Известен способ определения собственных форм колебаний конструкции [Вибрации в технике: Справочник. В 6-ти томах. - М.: Машиностроение, 1981, т.5, с.339.], согласно которому конструкцию подвергают многоточечному возбуждению и путем надлежащего выбора гармонических возмущающих сил с относительными фазовыми сдвигами 0° или 180° выделяют поочередно отдельно собственные тона и измеряют амплитуды колебаний отдельных точек конструкции при выделенных собственных формах колебаний.

Недостатком этого способа является быстрый износ конструкции вследствие длительных вибрационных испытаний в условиях резонанса и трудоемкость его осуществления.

Наиболее близким к заявляемому является способ определения собственных форм колебаний упругой конструкции (Патент №2058022, МКИ 6 G01М 7/02 - Способ определения эквивалентных масс упругой конструкции, соответствующих данной точке возбуждения и точке наблюдения / Вернигор В.Н. // Открытия. Изобретения. - 1996. - №10) в m заданных точках наблюдения B_j (j=1, 2, 3,...,m), при котором измеряют собственные частоты колебаний конструкции, возбуждают конструкцию на нескольких частотах, лежащих вне окрестности собственных частот.

Далее измеряют действительную часть динамической податливости конструкции и статическую податливость конструкции, при этом измеряют амплитуды изменения параметра наблюдения на каждой из частот возбуждения в каждой из m заданных точек, а также измеряют величину возбуждающего воздействия.

Из условия минимума специальной целевой функции определяют эквивалентные массы, соответствующие точке возбуждения и точкам наблюдения, а значение собственной формы колебаний в любой из заданных точек наблюдения определяют по формуле (2).

Недостатком данного способа является необходимость измерений динамической и статической податливости конструкции. Процедура таких измерений включает в себя измерение не только величины амплитуды изменения параметра наблюдения (виброперемещения, виброскорости, виброускорения, вибронапряжения), но и величины возбуждающего воздействия, что часто является невозможным по различным причинам, в частности по причине недоступности необходимых мест установки датчиков.

Технический результат, на достижение которого направлено изобретение, заключается в создании способа, исключающего измерение величины возбуждающего воздействия.

Для достижения названного технического результата в способе определения собственных форм колебаний упругой конструкции в m заданных точках наблюдения В_j (j=1, 2, 3,..., m) измеряют собственные частоты колебаний конструкции и возбуждают конструкцию на нескольких частотах, лежащих вне окрестности собственных частот.

Новым в заявляемом способе является то, что выбирают точку наблюдения А и измеряют амплитуды изменения параметра наблюдения на каждой из частот возбуждения в каждой из m заданных точек, а также в выбранной точке наблюдения А конструкции, при этом амплитуды изменения параметра наблюдения в каждой из m заданных точек В_j (j=1, 2, 3,..., m) и выбранной точке наблюдения А измеряют одновременно, определяют из условия минимума целевой функции

значения амплитудных функций , η_k(A), η_k(B_j), после чего определяют значения амплитудных функций, определяющих собственные формы колебаний конструкции в каждой заданной точке B_j:

где (k=2, 3,..., n),

y(A, Ω_i) - амплитуда колебаний в выбранной точке наблюдения А конструкции, измеренная на частоте возбуждения Ω_i (i=1, 2,......,N);

у(B_j, Ω_i) - амплитуда колебаний в каждой из заданных В_j точек конструкции, измеренная на частоте возбуждения Ω_i;

n - число определяемых форм колебаний;

N - число частот возбуждения;

- соотношение эквивалентных масс конструкции в точке наблюдения А и точке возбуждения О конструкции по k-той собственной форме колебаний

- соотношение эквивалентных масс конструкции в точке наблюдения β_j, и точке возбуждения О конструкции по k-той собственной форме колебаний.

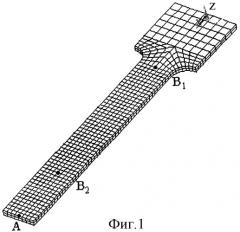
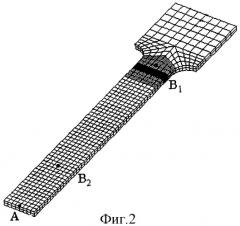
На прилагаемых фиг.1, 2 изображен рассматриваемый в качестве примера образец, закрепленный за широкий конец.

Способ определения собственных форм колебаний упругой конструкции осуществляется следующим образом.

Измеряют n собственных частот ω_i, ω₂,...,ω_n колебаний конструкции. Затем N раз возбуждают конструкцию на нескольких частотах, лежащих вне окрестности собственных частот ω₁, ω₂,...,, вызывая ее гармонические колебания с частотами возбуждения Ω₁, Ω₂,..., Ω_N. Выбирают точку наблюдения А и измеряют амплитуды изменения параметра наблюдения (виброперемещения виброскорости, виброускорения, вибронапряжения) на каждой из частот возбуждения Ω₁, Ω₂,... Ω_N, в каждой из m заданных точек В_j (j=1, 2, 3,...,m) и в выбранной точке наблюдения А конструкции. Амплитуды изменения параметра наблюдения в заданных точках В_j и выбранной точке А наблюдения измеряют одновременно.

Определяют из условия минимума целевой функции

значения величин , η_k(A), η_k(B_j),

после этого определяют значения амплитудных функций, определяющих собственные формы колебаний конструкции в каждой заданной точке В_j:

где (k=2, 3,..., n),

y(A, Ω_i) - амплитуда колебаний в выбранной точке наблюдения А конструкции, измеренная на частоте возбуждения Ω_i (i=1, 2,......,N);

y(B_j, Ω_i) - амплитуда колебаний в каждой из заданных В_j точек конструкции, измеренная на частоте возбуждения Ω_i;

n - число определяемых форм колебаний;

N - число частот возбуждения;

- соотношение эквивалентных масс конструкции в точке наблюдения А и точке возбуждения О конструкции по k-той собственной форме колебаний

- соотношение эквивалентных масс конструкции в точке наблюдения B_j и точке возбуждения О конструкции по k-той собственной форме колебаний.

В процессе минимизации используемой целевой функции происходит сглаживание экспериментальных данных (i=1, 2,..., N) по отношению амплитуд изменения параметра наблюдения (виброперемещения, виброскорости, виброускорения, вибронапряжения) в двух точках А и В конструкции методом наименьших квадратов. Причем в качестве базовой зависимости отношения от частоты возбуждения Ω принята зависимость

в то время как точная зависимость имеет вид

Выбор такой базовой зависимости и целевой функции позволяет при определении эквивалентных масс полностью учесть первые n форм колебаний конструкции.

Собственные частоты колебаний ω_k и амплитуду изменения параметра наблюдения (виброперемещения, виброскорости, виброускорения, вибронапряжения) измеряют, например, виброизмерительным комплексом АВДИ-1 [1].

Величины определяют из условия минимума целевой функции например, на основе вычислительных комплексов Maple, МАТЕМАТИКА.

ПРИМЕР.

Рассмотрены поперечные колебания жестко закрепленного образца, изображенного на фиг.1, 2. В расчетах образец был закреплен за свой широкий конец. При этом область образца, совершающая колебания (рабочая часть образца), представляла собой прямоугольный брус размером 0,110×0,015×0,0025 м. Для получения контрольных результатов на основе вычислительного комплекса ANSYS был выполнен модальный анализ и получены собственные частоты и формы колебаний образца. Первые две собственные частоты колебаний оказались равными ω_i=142,18 Гц, ω₂=926,33 Гц. При определении значений амплитуд колебаний образца было условно принято, что амплитуда колебаний точки А, расположенной в середине верхней границы крайнего поперечного сечения бруса (см. фиг.1, 2), равна единице. При этом амплитуда колебаний точки В, расположенной в середине средней линии верхней грани рабочей части образца (см. фиг.1, 2), оказалась равной

Для проверки данного изобретения был выполнен численный эксперимент, в котором вычислительным комплексом ANSYS были определены амплитуды колебаний у(В, Ω_i), у(А, Ω_i) точек В и А под действием гармонической силы, приложенной в точке А перпендикулярно плоскости образца. Значения амплитуд были вычислены при различных частотах возбуждения Ω_i. Значения этих частот и результаты вычислений представлены в таблице.

Таблица
Номер частоты возбуждения N	Частота возбуждения Ωi, Гц	y(A, Ωi), м	у(В, Ωi), м
1	40	0,1533Е-3	0,6191Е-4
2	60	0,1713E-3	0,6962Е-4
3	80	0,2052Е-3	0,8417Е-4
4	100	0,2762Е-3	0,1146Е-3
5	120	0,4823Е-3	0,2030Е-3
6	200	-0,1365E-3	-0,6256Е-4
7	260	-0,5448Е-4	-0,2752Е-4
8	300	-0,3554Е-4	-0,1951E-4
9	820	0,1163Е-4	-0,1160E-4
10	740	0,4494Е-5	-0,8140Е-5
11	660	0,6502Е-6	-0,7212Е-5
12	1040	-0,1456Е-4	0,6825Е-5
13	1140	-0,7847Е-5	0,3037Е-5

Далее согласно описанию изобретения была составлены целевая функция и определены значения величин , η₂(A), η₂(B), при которых эта функция достигает минимума. В результате расчетов получены следующие значения амплитуд колебаний точки В: (первая форма), (вторая форма). Сравнение данных результатов с контрольными значениями показывает, что погрешность определения амплитуд колебаний точки на основе предложенного изобретения является вполне удовлетворительной: по первой форме она составляет 0,07%, по второй - 0,4%.

Способ определения собственных форм колебаний упругой конструкции в m заданных точках наблюдения B_j (j=1, 2, 3,..., m), при котором измеряют собственные частоты колебаний конструкции, возбуждают конструкцию на нескольких частотах, лежащих вне окрестности собственных частот, отличающийся тем, что выбирают точку наблюдения А и измеряют амплитуды изменения параметра наблюдения на каждой из частот возбуждения в каждой из m заданных точек, а также в выбранной точке наблюдения А конструкции, при этом амплитуды изменения параметра наблюдения в каждой из m заданных точек B_j (j=1, 2, 3,..., m) и выбранной точке наблюдения А измеряют одновременно, определяют из условия минимума целевой функции

значения амплитудных функций , η_k(A), η_k(B_j), после чего определяют значения амплитудных функций, определяющих собственные формы колебаний конструкции в каждой заданной точке B_j:

,

где k=2, 3,...,n;

у(А, Ω_i) - амплитуда колебаний в выбранной точке наблюдения А конструкции, измеренная на частоте возбуждения Q_i (i=1, 2,..., N};

у(B_j, Q_i) - амплитуда колебаний в каждой из заданных B_j точек конструкции, измеренная на частоте возбуждения Ω_i;

n - число определяемых форм колебаний;

N - число частот возбуждения;

- соотношение эквивалентных масс конструкции в точке наблюдения А и точке возбуждения О конструкции по k-й собственной форме колебаний;

- соотношение эквивалентных масс конструкции в точке наблюдения B_j и точке возбуждения О конструкции по k-й собственной форме колебаний.