Магнитный двигатель

Магнитный двигатель

Иллюстрации

Показать все

Реферат

Изобретение относится к области физики магнетизма и может быть использовано в качестве источника механической энергии, получаемой от преобразования энергии магнитного поля, создаваемого постоянными магнитами.

Магнетизм - особая форма взаимодействия электрических токов и магнитов (тел с магнитным моментом) между собой и одних магнитов с другими магнитами. Магнитное взаимодействие пространственно разнесенных тел осуществляется через магнитное поле Н, которое, как и электрическое поле Е, представляет собой проявление электромагнитной формы движения материи. Между магнитными и электрическими полями нет полной симметрии, так как источниками электрических полей являются электрические заряды, а магнитные заряды - монополи пока не обнаружены, хотя теория предсказывает их существование. Источник магнитного поля - движущийся электрический заряд, то есть электрический ток. В атомных масштабах движение электронов и протонов создает орбитальные микротоки, связанные с переносным движением этих частиц в атомах или атомных ядрах, кроме того, наличие у микрочастиц спина обусловливает существование у них спинового магнитного момента. Поскольку электроны, протоны и нейтроны, образующие атомные ядра, атомы, молекулы и все макротела (газы, жидкости, кристаллические и аморфные твердые тела) имеют собственный магнитный момент, то, в принципе, все вещества подвержены влиянию магнитного поля - обладают магнитными свойствами, то есть являются магнетиками. Магнетики подразделяются на диамагнетики, парамагнетики и ферромагнетики. Последние имеют наибольшую магнитную восприимчивость и используются в технике в качестве эффективных магнитов. В них атомные магнитные моменты спонтанно коллинеарно самоориентируются, образуя аномально большие магнитные моменты. У современных магнитных материалов энергетическое произведение (В Н)_max достигает величины 320 Тл·кА/м (40 млн Гс·Э), например, у материала с высокой коэрцитивной силой SmCo₃ (см., напр., Преображенский А.А., Биширд Е.Г. Магнитные материалы и элементы, 3 изд., М., 1986; Февралева И.Е. Магнитотвердые материалы и постоянные магниты. К., 1969; Постоянные магниты. Справочник, М., 1971).

Сложность атомной структуры веществ, построенных из огромного числа микрочастиц, дает практически неисчерпаемое разнообразие их магнитных свойств, связь которых с немагнитными свойствами (электрическими, механическими, оптическими и др.) позволяет использовать исследования магнитных свойств для получения информации о внутренней структуре и других свойствах микрочастиц и макротел. Отметим, что магниты обладают внутренней энергией. В случае однородного магнитного поля в объеме магнита V энергия запасенного магнитного поля W˜μ₀Н²V/2. Причем эта величина энергии практически не расходуется при силовых взаимодействиях с другими магнетиками и сохраняется благодаря постоянному движению заряженных микрочастиц вещества.

Известно силовое взаимодействие магнитных полей, создаваемых двумя магнитными системами, например, в электрических двигателях, состоящих из подвижного вращающегося ротора и неподвижного статора. В синхронных многофазных двигателях переменного тока в статоре образуется вращающееся магнитное поле, увлекающее за собой намагниченный постоянно ротор: его полюс S постоянно притягивается к полюсу N статора, а противоположный полюс N ротора притягивается полюсом S статора. В коллекторных двигателях постоянного тока, наоборот, вращающиеся за счет работы коллектора магнитные полюса ротора приводят во вращение ротор относительно статора так, что всегда противоположные полюсы статора и ротора тяготеют друг к другу.

Известно, что одноименные полюсы двух магнитных систем отталкивают друг друга, что в технике используется, например, для получения так называемой магнитной подушки, с целью снижения трения при вращении, например в гироскопии.

Ближайшим аналогом (прототипом) заявляемому техническому решению является способ силового взаимодействия магнитного поля магнита с магнитным полем, образованным электрическим током в соленоиде, рамке с током, в роторе, статоре двигателя, в электромагните и др. физических и технических объектах на основе закона электромагнитной индукции Фарадея и закона Био-Савара (см., напр., Краткий справочник по физике, Г.Эберт, пер. со 2-го нем.изд. под ред. К.П.Яковлева, ГИФМЛ, М., 1963, с.434-436).

Недостатком известного технического решения при получении механической энергии при взаимодействии магнитных полей является затрата энергии от ее источника с коэффициентом полезного действия, всегда меньшим единицы, поскольку при прохождении в проводнике электромагнитной системы электрического тока имеют место потери на нагревание проводника, и эти тепловые потери невосполнимы.

Известно, что закон Ома применим к магнитным цепям, однако при этом магнитный ток в магнитной цепи с соответствующим магнитным сопротивлением не создает тепловых потерь, то есть магнитная энергия постоянного магнита не расходуется и не превращается в тепло. В этом смысле постоянный магнит, если абстрагироваться от так называемого старения магнита, является «вечным» источником магнитного поля с заданной величиной энергии. Это обстоятельство создает предпосылки к использованию энергии практически неисчерпаемого магнитного поля для получения механической работы.

Заявляемое техническое решение - магнитный двигатель, содержащий постоянные магниты и вращающийся ротор из ферромагнитного вещества, отличающийся тем, что вращающийся ротор из ферромагнитного вещества выполнен, например, в виде кольца или полого шара, внутри которого неподвижно закреплен первый постоянный магнит прямой формы, а снаружи от него неподвижно закреплен второй постоянный магнит подковообразной формы, магнитные поля первого и второго постоянных магнитов взаимно скрещены, а постоянная релаксации магнитной вязкости Т ферромагнитного вещества ротора выбрана, например, равной τ≈0,09/ω_уст. где ω_уст. - угловая скорость вращения ротора в установившемся режиме.

Поставленная цель - получение механического вращения ротора из ферромагнитного вещества в скрещенных магнитных полях внутреннего и внешнего постоянных магнитов - достигается благодаря различию сил, действующих на намагничивающийся ротор со стороны указанных постоянных магнитов, что отвечает различным по величине и противоположным по направлению вращающим моментам, приложенным к указанному ротору, разность которых определяет результирующий вращающий момент, раскручивающий ротор до угловой скорости, ограниченной величиной момента нагрузки (с учетом трения вращения) и магнитной вязкостью ферромагнитного вещества ротора с заданной постоянной времени процесса его перемагничивания.

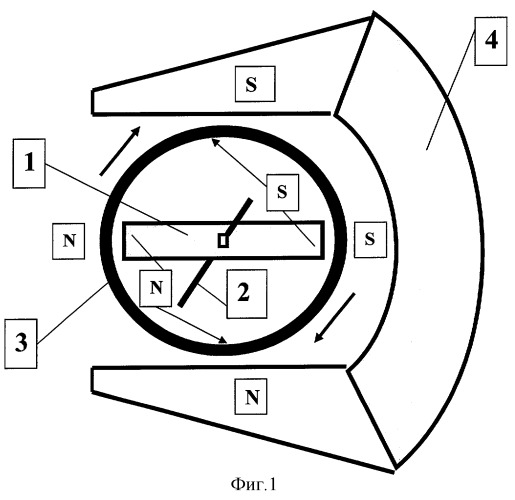
Устройство одного из вариантов построения магнитного двигателя с вращающимся ротором из ферромагнитного вещества в форме кольца представлено на фиг.1. Оно состоит их внутреннего первого постоянного магнита 1, вращающегося на оси 2 кольцевого ротора 3 из ферромагнитного вещества и внешнего второго постоянного магнита 4, причем магниты 1 и 4 закреплены неподвижно, а их магнитные поля взаимно ортогональны в области расположения ротора 3. Магнитные зазоры между магнитами 1 и 4 и ротором 3 выбраны минимальными, а магнитная индукция магнитов 1 и 4 определяет энергетику устройства.

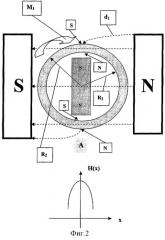
На фиг.2 указаны магнитные полярности намагниченного первым магнитом 1 ферромагнитного вещества ротора 3 и возникающий при этом вращающий момент M₁, направленный по часовой стрелке.

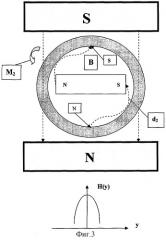
На фиг.3 указаны магнитные полярности намагниченного вторым магнитом 4 ферромагнитного вещества ротора 3 и возникающий при этом вращающий момент М₂, направленный против часовой стрелки. На фиг.2 и 3 представлены также эпюры напряженностей магнитного поля, наведенного в соответствующих участках наружной А (для фиг.2) и внутренней В (для фиг.3) поверхностей кольцевого ротора 3, указаны геометрические параметры устройства ротора 3 - радиусы кольца R₁ и R₂, причем R=(R₁+R₂)/2 - средний радиус кольцевого ротора, а также показаны магнитные силовые линии соответствующих магнитных цепей раздельно по действию магнитов 1 и 4 на ротор 3.

Рассмотрим действие заявляемого устройства.

При неравенстве абсолютных величин моментов M₁ и М₂ результирующий вращающий момент, приложенный к ротору 3, равен ΔM=M₁-М₂≠0. Различие указанных моментов достигается самой конфигурацией магнитных цепей магнитов 1 и 4 и ротора 3. Пусть, например, M₁>М₂. В этом случае ротор 3 будет вращаться на оси 2 по часовой стрелке. Поскольку при вращении ротора 3 из ферромагнитного вещества максимумы его намагниченности постоянно смещаются вдоль образующей кольца для системы координат, связанной с ротором, оставаясь неподвижными в системе координат неподвижно закрепленных первого 1 и второго 4 постоянных магнитов, результирующий вращающий момент ΔM действует постоянно во времени, раскручивая ротор 3 при условии, что этот вращающий момент больше момента нагрузки М_нагр на ось 2 с учетом ее момента трения (ΔМ>М_нагр).

Поскольку намагниченность ферромагнитного вещества при включении магнитного поля устанавливается во времени по закону ΔI(t)=ΔI_m[1-ехр(-t/τ)], где ΔI_m - установившееся (наибольшее возможное) значение разности намагничивании ферромагнетика от магнитов 1 и 4 для заданных значений их магнитных полей, τ - постоянная релаксации магнитной вязкости для выбранного ферромагнитного вещества ротора 3, то с увеличением угловой скорости вращения ω ротора 3 снижается величина результирующего магнитного момента ΔМ(ω), так как ΔМ(ω)˜ΔI(t) при t=ατ, где α=Δs/ωτR, Δs - продольный размер вдоль кольца ротора, внутри которого намагниченность максимальна с уровнем, например, 0,9 ΔI_m, R - радиус кольца ротора 3. Таким образом, получаем ΔМ(ω)=0,9βΔI_m=βΔI_m[1-ехр(-Δs/ωτR)], где β - размерный коэффициент пропорциональности, устанавливаемый опытным путем и зависящий от конструкции устройства (в частности, от величины магнитных зазоров между постоянными магнитами 1 и 4 относительно кольцевого ротора 3, а также от конструкции полюсов этих магнитов).

Момент трения оси 2 ротора 3 М_тр(ω), напротив, растет линейно с увеличением угловой скорости ω вращения ротора, то есть М_тр(ω)=μω, где μ - размерный коэффициент. Полагая присоединенный момент нагрузки М_пр.н. неизменным, не зависящим от скорости вращения ротора 3, находим уравнение для нахождения угловой скорости ω вращения ротора 3 в виде ΔМ(ω)=М_пр.н.+М_тр(ω), откуда его явное выражение имеет вид: βΔI_m [1-ехр(-Δs/ωτR)]=М_пр.н.+μω, и при заданных величинах конструктивных параметров устройства и величине присоединенного момента нагрузки легко найти угловую скорость ω вращения ротора 3. При этом в установившемся режиме с угловой скоростью ω_уст присоединенный момент нагрузки М_пр.н.=βΔI_m[1-ехр(-Δs//ω_устτR)]-μω_уст определяет получаемую от магнитного двигателя механическую работу. Полагая величину ехр (-Δs/ω_устτR)=0,1 при k=Δs/R (можно принять, что k=0,2), выбор ферромагнитного вещества для ротора 3 должен удовлетворять условию достижения заданной величины намагниченности ферромагнетика, например, до уровня 0,9 ΔI_m в течение промежутка времени Δt=Δs/ω_уст R=2,2 τ, так что находим выражение для постоянной релаксации τ магнитной вязкости ферромагнитного вещества ротора 3 в виде τ=k/2,2 ω_уст≈0,09/ω_уст. Отметим, что ассортимент ферромагнетиков позволяет выбирать требуемые значения τ, так как эта величина находится для разных ферромагнетиков в чрезвычайно широком диапазоне - от 10^-9 с до нескольких десятков часов.

Намагничивание ферромагнитного вещества ротора 3 со стороны постоянного магнита 1 равно I_m1 (соответствует фиг.2), а намагничение со стороны магнита 4 равно I_m2 (соответствует фиг.3), так что ΔI_m=I_m1 -I_m2. При этом вращающий момент M_i определяется силой F₁, приложенной ортогонально радиусу R ротора 3 и возникающей от силового взаимодействия намагниченности I_m1 ферромагнетика ротора 3 с магнитным полем второго постоянного магнита 4, а вращающий момент М₂ - силой F₂, приложенной ортогонально радиусу R ротора 3 и возникающей от силового взаимодействия намагниченности I_m2 ферромагнетика ротора 3 с магнитным полем первого постоянного магнита 1. Причем указанные силы ортогональны друг другу в силу ортогональности исходных магнитных силовых линий для магнитов 1 и 4, а также не равны друг другу по абсолютной величине, а именно F₁>F₂ при заданных конструктивных параметрах устройства, что и создает неуравновешенный вращающий момент ΔM=M₁-М₂≠0.

Как известно, сила, действующая между полюсами с магнитными потоками Ф₁ и Ф₂ на сравнительно большом расстоянии d, равна F=Ф₁Ф₂/4πμ₀d², где μ₀ - абсолютная магнитная проницаемость (μ₀=8,85.10^-12 Ф/м). Намагниченность ферромагнитного кольца ротора 3, образованная соответствующими магнитами 1 и 4, может быть эквивалентно представлена как действие образованных магнитов на соответствующих участках кольца - соответственно на наружной части кольца вблизи магнита 1 (зона А на фиг.2) и на внутренней части кольца вблизи магнита 4 (зона В на фиг.3, в низшей точке кольца). При этом можно полагать, в первом приближении, что произведение магнитных потоков Ф₁ Ф₂, образованных между указанными полюсами наведенных в кольце магнитов и магнитами 4 и 1 соответственно, в обоих случаях взаимодействия оказывается одинаковым. Однако расстояние между областью максимальной намагниченности кольца, вызванной действием первого (внутреннего) постоянного магнита 1, несколько больше радиуса кольца d₁>R, a расстояние между областью максимальной намагниченности кольца, вызванной действием второго (внешнего) постоянного магнита 4, несколько меньше величины (2)^1/2 R, то есть d₂<1,41 R. Следовательно, силы взаимодействия между соответствующими парами полюсов отличаются между собой почти в 2 раза, так как (d₂/d₁)²≈2. Кроме того, сила F₁ ортогональна радиусу кольца R, а сила F₂ - суть проекция на касательную к радиусу кольца от силы, действующей под углом, близким к π/4, то есть составляет от последней часть около 0,707 ее значения. Для идеализированного случая тонкого ферромагнитного кольца с минимальными зазорами между магнитами 1 и 4 и кольцом ротора 3 получаются соотношения сил F₂/F₁=0,707/2=0,353, что означает в этом случае превышение вращающего момента M₁ над вращающим моментов М₂ почти втрое, тогда ΔМ=0,646 M₁=0,646 F₁R=0,162 Ф₁Ф₂/πμ₀R, где Ф₁ - магнитный поток с наружного участка кольца максимальной намагниченности, расположенного вблизи первого постоянного магнита 1, а Ф₂ - аналогичный магнитный поток, образованный вторым постоянным магнитом 4. Корректное решение задачи по определению сил F₁ и F₂ обеспечивается интегрированием с учетом конфигурации магнитных силовых линий и топологии магнитных полюсов 1 и 4 и распределения напряженности магнитного поля в ферромагнитном кольце ротора 3, поэтому вышеприведенная оценка является лишь приблизительной, качественной, не претендующей на строгость.

По правилам механики мощность на оси 2 рассмотренного магнитного двигателя, которую можно сообщить механической нагрузке, равна N_н≈(0,9ΔМ-μω_уст)ω_уст при выборе ферромагнетика ротора 3 с величиной постоянной τ≈0,09/ω_уст. Видно, что для приведения ротора 3 во вращательное состояние необходимо, чтобы коэффициент μ мог быть задан как μ<0,9ΔМ/ω_уст, что указывает на имеющееся при работе устройства ограничение по росту угловой скорости ротора 3 при заданном значении величины ΔM, определяемой энергетикой применяемых постоянных магнитов 1 и 4. При выполнении указанного неравенства устройство работает в так называемом «мягком режиме самовозбуждения», то есть приводится во вращательное движение с доведением угловой скорости вращения ротора 3 до значения ω_уст без сообщения ротору какого-либо внешнего толчка (вращательного момента), причем направление вращения всегда жестко определено магнитными полярностями постоянных магнитов 1 и 4 в заданной конструкции и может изменяться на противоположное при смене полярностей любого из названных магнитов.

Следует указать на важное обстоятельство. Магнитный поток первого постоянного магнита 1 в значительной своей части замыкается по внутренней части кольцевого ротора, однако частично намагничивает кольцо с максимумами намагниченности около полюсов N и S магнита 1, которое снаружи становится обладающим свойством магнита с сохранением полярностей магнита 1 (как видно из фиг.2). То же самое относится и к появлению максимумов намагниченности кольца вблизи полюсов постоянного магнита 4 с сохранением полярности этого магнита на внутренних частях кольца (как видно из фиг.3), хотя основной магнитный поток постоянного магнита 4 замыкается по внешней части кольца ротора 3. Таким образом, кольцо из ферромагнитного материала (или полый шар в случае выполнения ротора 3 в форме полого шара со стенками из ферромагнитного вещества) является магнитным экраном несовершенного действия, то есть частично выпускающего наружу этого экрана магнитные поля для соответствующих магнитных цепей с заданными распределениями напряженностей магнитных полей на этих наружных частях «магнитного экрана», что и используется при работе устройства. Следует при этом отметить, что каждый из постоянных магнитов 1 и 4 создает магнитные поля, составляющие которых, замыкающиеся по соответствующим поверхностям ферромагнитного кольца ротора 3, не создают каких-либо вращающих моментов в этом кольце, а неуравновешенный вращающий момент в кольце возникает как следствие различия расстояний от зоны А (фиг.2) до полюса постоянного магнита 4 и от зоны В (фиг.3) до полюса магнита 1 (для тонкого кольца эти расстояния, как указывалось выше, различаются в 1,41 раза), а также из-за различия в углах действия сил магнитного сцепления (в одном случае сила магнитного сцепления ортогональна радиусу кольца, а в другом - направлена к нему под углом, близким к π/4). В силу однородности магнитных свойств кольца ротора 3 по всему его объему вращение ротора не изменяет действующего вращающего момента ΔМ для заданного значения угловой скорости ω.

Для примера можно указать, что при вращении ротора 3 со скоростью 3000 об/мин оптимальной величиной постоянной релаксации магнитной вязкости ферромагнитного вещества ротора является τ≈290 мкс.

Известный принцип возрастания энтропии и первое и второе начала термодинамики оперируют с теплоэнергетическими преобразованиями, которые всегда (кроме состояния равновесия) идут с затратой энергии при совершении какой-либо работы, большей той, которая составляет саму проделанную работу, а часть затраченной энергии безвозвратно превращается в тепловую. Поэтому к.п.д. всех известных преобразователей энергии всегда меньше единицы. Однако в микромире действует иной процесс: движение микрочастиц обусловлено тепловой энергией - импульс р движения микрочастиц массой m₁ определяется как р²/2m₁=(3/2)kT, где k - постоянная Больцмана, Т - температура по шкале Кельвина, а соударения микрочастиц между собой вызывают тепловые процессы - среда нагревается, то есть происходит самовоспроизводящийся обмен энергией, при котором беспредметно говорить о тепловых потерях, поскольку тепловая энергия и является источником движения микрочастиц, а это движение порождает саму тепловую энергию. На поддержание хаотического движения микрочастиц и, следовательно, хаотического распределения магнитных моментов (спинов) в веществе, при котором оно не обнаруживает ощутимых магнитных свойств, затрачивается, по-видимому, больше энергии, чем для тех микрочастиц, которые имеют упорядоченное расположение их магнитных моментов. Поэтому высвободившаяся в результате упорядочения микрочастиц (доменов) часть энергии как раз и составляет энергию магнитного поля. Эта энергия самовосполняемая, определяемая природой процессов превращения энергии на микроуровне.

Однако остается неясным вопрос, каким образом механическая работа, совершаемая действием постоянного магнитного поля на магнитные тела или другие магниты, осуществляется без потери энергии магнитного поля. Ведь факт, что работа магнитных сил не приводит к исчезновению намагниченности постоянных магнитов. Работа совершается действием сил, в частности, магнитных сил. По третьему закону Ньютона действие силы вызывает равное и противоположно направленное силовое противодействие. В случае с силовым действием постоянных магнитов возникает вопрос об их источнике энергии, вопрос о том, какой объект затрачивает энергию, а какой ее получает. Но, возможно, нет ни того, ни другого, оба объекта - магнит и притягиваемое или отталкиваемое им тело - оказывают друг на друга силовое воздействие. А поскольку магнит при этом не теряет своей энергии, то из этого следует вывод, что магнит как бы восполняет «потраченную» на перемещение тела своей силой энергию за счет обратного силового действия со стороны этого тела, хотя природа этого преобразования пока не понятна.

Таким образом, постоянные магниты потенциально являются источниками энергии, своеобразными неистощимыми аккумуляторами, «подзаряд» которых осуществляется непрерывно во времени за счет происходящих процессов превращения энергии на молекулярном уровне. «Запуск» в работу таких «аккумуляторов» как толчок к началу осуществления указанных молекулярных процессов производится от внешних источников однократно на этапе создания постоянных магнитов путем доведения специальных ферромагнитных материалов с высокой коэрцитивной силой до их насыщения в магнитном поле соленоидов с током намагничивания и необходимой технологической тренировки магнитов по известным правилам.

Возможной модификацией заявляемого устройства является использование постоянных магнитов 1 и 4 не с плоскими полюсами, а сферическими - для ротора в форме полого шара или сферически-цилиндрическими - для ротора кольцевого типа, что снижает магнитное сопротивление цепей с такими магнитами.

Излишне говорить, что применение магнитных двигателей рассмотренного типа и аналогичных конструкций, использующих постоянные магниты, вместо электромагнитных двигателей, требующих затраты электрической энергии от постороннего ее источника, представляет большой интерес для энергетики. Физические основы работы таких двигателей представляют самостоятельный интерес для физиков-теоретиков, занимающихся проблемами магнетизма. Они должны со временем открыть этот феномен восполнимости энергии магнитного поля постоянных магнитов, независимо от их силового действия, без учета фактора естественного старения в таких магнитах.

Магнитный двигатель, содержащий постоянные магниты и ротор из ферромагнитного вещества, отличающийся тем, что ротор из ферромагнитного вещества выполнен в виде кольца или полого шара, внутри которого неподвижно закреплен первый постоянный магнит, а снаружи от него неподвижно закреплен второй постоянный магнит подковообразной формы, причем магнитные поля первого и второго постоянных магнитов взаимно ортогональны в области расположения ротора и действуют на него с различными магнитными силами, постоянная времени τ процесса перемагничивания ферромагнитного вещества ротора равна τ≈0,09/ω_уст., где ω_уст. - расчетная угловая скорость вращения ротора в установившемся режиме.