Способ умножения частоты аналогового косинусоидального колебания

Способ умножения частоты аналогового косинусоидального колебания

Иллюстрации

Показать все

Реферат

Изобретение относится к области информационных технологий в радиотехнике, может быть использовано в системах многоканальной передачи сообщений и позволяет из одного аналогового косинусоидального колебания стабильной частоты сформировать N гармоник стабильной частоты с минимально возможным уровнем паразитных побочных дискретных спектральных составляющих, а также осуществить угловую модуляцию гармоник без сопутствующей паразитной амплитудной модуляции при условии, что в результате применения предлагаемого способа реализуется алгоритм:

где Y_n(X) - сигнал n-й гармоники

Х=cos(ω₀t) - аналоговое колебание стабильной частоты ω₀;

n - номер гармоники, принимающий значения 1, 2, ..., N;

S_n - n-й информационный сигнал, причем .

Известен способ умножения частоты, при использовании которого колебания N частот формируют из одного колебания стабильной частоты (например, из колебания эталонного кварцевого генератора) путем нелинейного преобразования - прямого умножения колебания стабильной частоты, что позволяет сформировать дискретное множество N частот [1, стр.10, 12, 94-99]. Для этого способа серьезной оказывается проблема фильтрации паразитных побочных дискретных спектральных составляющих. При применении этого способа в радиотехнических схемах значительно возрастает количество фильтров, а для осуществления угловой модуляции сформированных гармоник в схемы требуется дополнительно включить N модуляторов. Следовательно, схемы усложняются, а при угловой модуляции гармоники не исключена возможность появления сопутствующей паразитной амплитудной модуляции (ПАМ).

Более простыми средствами подавлять нежелательные дискретные составляющие в спектре выходного колебания позволяют способы косвенного умножения частоты. Косвенное умножение частоты стабильного колебания без заметного снижения стабильности частоты гармоники можно реализовать, используя фазовую автоподстройку частоты подстраиваемого генератора по опорному колебанию стабильной частоты (например, по колебанию кварцевого генератора) [2, стр.227 и рис.9.1], [3]. При этом в кольце автоподстройки частота колебания подстраиваемого генератора делится на число, равное номеру формируемой гармоники. Для этого в состав кольца автоподстройки вводят делители частоты. При таком способе умножения возможна угловая модуляция гармоники. Однако при использовании гармонических делителей частоты приходится решать проблему расширения диапазона рабочих частот умножителя [3]. Применение импульсных делителей частоты позволяет расширить полосу рабочих частот, однако для формирования по этому способу нескольких гармоник (дискретного множества частот) [1] требуется косвенный синтез частот, и схемы устройств фазовой синхронизации заметно усложняются.

При умножении стабильной частоты в n раз нежелательные побочные дискретные спектральные составляющие не возникают, если применить способ, согласно которому косинусоидальное колебание стабильной частоты подвергают нелинейному преобразованию по закону функции Чебышева первого рода n-го порядка путем подачи этого колебания на вход нелинейного элемента с указанной характеристикой [4, стр.426-428, 459-460]:

где Y_n(X) - сигнал на выходе нелинейного элемента (сигнал n-й гармоники);

Х=cos(ω₀t) - сигнал на входе нелинейного элемента (сигнал стабильной частоты ω₀);

n - коэффициент умножения частоты.

Этот способ использован в умножителе частоты в три раза, выполненном по мостовой схеме умножения, построенной из аналоговых емкостных элементов [4, стр.427, рис.5.117 и рис.5.118]. Однако в этом случае требуется очень точный подбор характеристик элементов моста схемы умножения, и без применения дополнительного модулятора невозможно осуществить угловую модуляцию колебания гармоники.

Наиболее близким по технической сущности является способ умножения частоты аналогового косинусоидального колебания при отсутствии побочных дискретных спектральных составляющих, заключающийся в следующем [4, стр.427]. Колебание стабильной частоты подают на диагональ емкостного моста, в противоположные ветви которого включены линейные и нелинейные электрические конденсаторы. Подбирают форму вольт-кулоновых характеристик нелинейных конденсаторов таким образом, чтобы их можно было с высокой точностью аппроксимировать функцией Чебышева первого рода 3-го порядка. Т.к. напряжение, снимаемое с другой диагонали моста, есть разность между напряжениями в ветвях моста с нелинейными и линейными конденсаторами, формируют зависимость сигнала третьей гармоники, описываемую функцией Чебышева первого рода третьего порядка:

где Y₃(X) - сигнал 3-й гармоники (сигнал на выходе умножителя);

Х=cos(ω₀t) - сигнал стабильной частоты ω₀ (сигнал на входе емкостного моста).

Однако такой способ умножения частоты на три требует очень точного подбора характеристик электрорадиоэлементов емкостного моста, а также не позволяет одновременно сформировать множество из N гармоник стабильной частоты и осуществить угловую модуляцию каждой из них для организации многоканальной передачи данных.

Задачей изобретения является обеспечение точности формирования требуемой нелинейной характеристики с целью создания множества из N гармоник стабильной частоты с возможностью осуществления угловой модуляции каждой из них.

В изобретении достигается следующий технический результат:

- способ позволяет с помощью одного генератора аналогового косинусоидального колебания стабильной частоты сформировать N гармоник стабильной частоты с минимальным уровнем побочных дискретных спектральных составляющих, избежать взаимного влияния гармоник, повысить чистоту спектра формируемых колебаний, не предъявляя при этом жестких требований к цепям фильтрации;

- способ позволяет осуществлять угловую модуляцию каждой из сформированных гармоник аналогового косинусоидального колебания без применения дополнительных модуляторов и без паразитной амплитудной модуляции.

Указанный технический результат достигается благодаря тому, что в способе, основанном на том, что аналоговое косинусоидальное колебание стабильной частоты подвергают нелинейному преобразованию по закону функции Чебышева первого рода, осуществляют аналого-цифровое преобразование косинусоидального колебания стабильной частоты, цифровой сигнал стабильной частоты подвергают арккосинусному преобразованию, а в каждом из n каналов осуществляют аналого-цифровое преобразование информационного сигнала, формируют цифровой сигнал номера гармоники стабильной частоты, цифровой информационный сигнал суммируют с сигналом номера гармоники и полученный суммарный сигнал перемножают с цифровым сигналом стабильной частоты. Таким образом, в каждом канале реализуется следующий алгоритм цифровой обработки указанных сигналов:

где Y_n(X) - сигнал n-й гармоники;

Х=cos(ω₀t) - аналоговое колебание стабильной частоты ω₀;

n - номер гармоники, принимающий значения 1, 2, ..., N;

S_n - n-й информационный сигнал, причем .

Данный алгоритм обработки позволяет осуществить угловую модуляцию гармоники без образования побочных дискретных спектральных составляющих, обусловленных умножением частоты. Действительно, если в n-ом канале отсутствует информационный сигнал (S_n=0), то алгоритм осуществляет нелинейное преобразование косинусоидального колебания по закону функции Чебышева первого рода n-го порядка, что, как показано в [4], соответствует умножению частоты этого колебания в n раз без образования гармоник с другими номерами.

Если же в алгоритме произвести подстановку значения Х=cos(ω₀t) и выполнить очевидные тригонометрические преобразования, то получим запись алгоритма формирования сигнала с угловой модуляцией.

Цифровой сигнал после обработки по рассматриваемому алгоритму подвергают цифро-аналоговому преобразованию, результатом которого является колебание с угловой модуляцией.

Таким образом, технический результат достигается за счет применения цифровой обработки сигнала генератора стабильной частоты и информационных сигналов, что позволяет устранить недостатки прототипа и аналогов и реализовать данный способ на базе процессора цифровой обработки сигналов.

По существу, общим между изобретением и прототипом является подход к задаче умножения стабильной частоты косинусоидального колебания, причем частота гармоник равна или кратна стабильной частоте. При этом формирование колебаний осуществляется на основе алгоритма, определяемого функцией Чебышева первого рода.

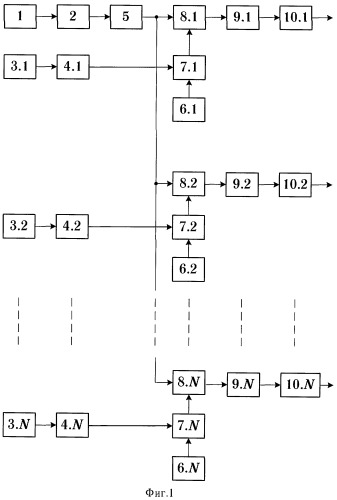
На фиг.1 изображена структурная схема устройства, с помощью которого реализуется способ умножения частоты; на фиг.2 приведены результаты численного моделирования.

Способ может быть реализован следующим образом (фиг.1).

Аналоговое косинусоидальное колебание с выхода источника стабильной частоты 1 подвергают аналого-цифровому преобразованию в блоке 2, а сигналы с выходов источников информационных сигналов 3.1, ..., 3.N подвергают аналого-цифровому преобразованию, соответственно, в блоках 4.1, ..., 4.N. Переход от аналогового представления сигналов к цифровому и позволяет осуществить дальнейшую их обработку с любой заданной точностью. Преобразованный в 2 сигнал источника стабильной частоты подвергают арккосинусному преобразованию в блоке 5. Формируют в блоках 6.1, ..., 6.N цифровые сигналы номеров гармоник стабильной частоты. Подвергнутые аналого-цифровому преобразованию в блоках 4.1, ..., 4.N сигналы источников сообщений суммируют в блоках 7.1, ..., 7.N с выходными сигналами соответствующих блоков формирования номера гармоники 6.1, ..., 6.N. Полученные в блоках 7.1, ..., 7.N суммарные сигналы перемножают соответственно в блоках 8.1, ..., 8.N с выходным сигналом блока 5. Если в каком-то из каналов отсутствует сигнал источника сообщения, то в этом канале осуществляют только умножение частоты исходного косинусоидального колебания частоты путем нелинейного преобразования по закону функции Чебышева первого рода. Суммирование же сигнала номера гармоники и сигнала источника сообщения позволяет осуществить угловую модуляцию гармоники, соответствующей рассматриваемому каналу. После перемножения сигналы подвергаются косинусному преобразованию в блоках 9.1, ..., 9.N, а затем цифро-аналоговому преобразованию в блоках 10.1, ..., 10.N, вследствие чего на выходах блоков 10.1, ..., 10.N имеют колебания гармоник, промодулированные сигналами соответствующих источников сообщений, которые могут быть поданы на сумматор и далее на модулятор несущей в радиопередающем устройстве многоканальной системы связи.

На фиг.2 приведена спектрограмма, полученная в результате численного моделирования предлагаемого способа в случае двух каналов. В качестве информационного сигнала в обоих каналах был использован процесс с нормальным распределением, подвергнутый низкочастотной фильтрации. Серый цвет линий соответствует амплитудному спектру модулированной гармоники 15-го порядка, а черный - спектру гармоники 20-го порядка (f₀ - частота исходного аналогового колебания, формируемого в блоке 1 на Фиг.1). Из приведенной спектрограммы можно сделать вывод о возможности организации многоканальной системы связи на основе предлагаемого способа, а дополнительная обработка информационных сигналов и фильтрация получаемых в каждом канале модулированных колебаний позволит передавать информацию на гармониках, отстоящих друг от друга на минимальное расстояние, равное трем, без наложения спектров и, следовательно, без возникновения перекрестных помех между каналами.

Таким образом, возможность реализации способа подтверждается результатами моделирования и исследования характеристик модели умножителя частоты.

Источники информации

1. Левин В.А. Стабилизация дискретного множества частот. - М.: Энергия, 1970.

2. Шапиро Д.Н., Паин А.А. Основы теории синтеза частот. - М.: Радио и связь, 1981.

3. А.С. №678633 (СССР). Умножитель частоты. МКИ: Н03В 14/00 / Е.С.Беспалов, А.Г.Демьянченко, Е.П.Смицкой, Е.А.Хуртин. - Опубл. в БИ №29, 1979.

4. Филиппов Е. Нелинейная электротехника. Пер. с нем. Под ред. А.Б.Тимофеева - М.: Энергия, 1976.

Способ умножения частоты аналогового косинусоидального колебания, основанный на том, что аналоговое косинусоидальное колебание стабильной частоты подвергают нелинейному преобразованию по закону функции Чебышева первого рода, отличающийся тем, что осуществляют аналого-цифровое преобразование аналогового косинусоидального колебания стабильной частоты, цифровой сигнал стабильной частоты подвергают арккосинусному преобразованию, а в каждом из дополнительно введенных n каналов осуществляют аналого-цифровое преобразование соответствующего информационного сигнала, формируют цифровой сигнал, соответствующий номеру гармоники стабильной частоты, который суммируют с преобразованным соответствующим информационным сигналом и полученный суммарный сигнал перемножают с преобразованным цифровым сигналом стабильной частоты, полученный после перемножения сигнал подвергают косинусному, а затем цифроаналоговому преобразованию.