Способ кодирования-декодирования информации в системах передачи данных

Способ кодирования-декодирования информации в системах передачи данных

Иллюстрации

Показать все

Реферат

Изобретение относится к технике связи и может быть использовано в системах передачи данных, преимущественно без обратной связи, для осуществления помехоустойчивого кодирования и декодирования информации каскадным кодом.

Известен "Способ и устройство для коррекции ошибок в системе связи" по патенту США №5996103. Известный способ для кодирования и декодирования информации каскадным кодом реализуется за счет использования в качестве внешнего кода недвоичных кодов, например кодов Рида-Соломона (PC), а в качестве внутреннего кода - сверточного кода, декодирование которого осуществляется с помощью декодера Витерби [1].

Данный способ требует наличия между кодером PC и сверточным кодером перемежителя и деперемежителя на передающей и приемной сторонах соответственно, чтобы минимизировать влияние пакетов ошибок. Внешний кодер PC не поддается влиянию ошибок, которые возникают в пределах одного символа, но рабочие характеристики декодера PC ухудшаются более длинными пакетами ошибок, появляющимися между последовательными символами, как это может происходить при работе декодера Витерби. Как следствие, требуется перемежение символов внешнего кода PC между символами внутреннего декодера Витерби для минимизации коррелированных ошибок. Кроме того, декодер Витерби требует большого объема памяти для хранения промежуточных состояний.

Указанных недостатков лишены системы кодирования-декодирования информации, в которых не применяется декодер Витерби, а в качестве внутреннего кода используются короткие двоичные блочные коды.

Наиболее близким к предлагаемому техническому решению является способ кодирования-декодирования информации, описанный в патенте США №6374382 "Сокращенный блочный код для систем каскадного кодирования" [2]. Данная система передачи данных использует каскадный код, внешний код которого - код PC, формирующий внешнюю кодовую последовательность на основе исходных данных, внутренний код - сокращенный блочный код (n, k,), причем k=8×i,

где i - небольшое целое число, выбираемое для того, чтобы избежать перемежения между внутренним и внешним кодами.

Известная система передачи данных работает следующим образом. В режиме кодирования информация от источника данных поступает на внешний кодер PC, который обеспечивает внешнее кодирование данных. Данные от кодера PC поступают на внутренний кодер, который обеспечивает внутреннее кодирование данных. Закодированные данные поступают на модулятор и передаются по каналу связи как каскадный сигнал.

В соответствии с первым вариантом реализации данного изобретения внутренний код (12, 8, 3) представляет собой модифицированный код Хэмминга (15, 11). Восьмибитовое информационное слово содержит последовательность а₀, a₁, а₂, а₃, а₄, а₅, а₆, а₇, а кодовое слово сформировано из последовательности а₇, а₆, a₅, а₄, а₃, а₂, a₁, а₀, Р₃, Р₂, Р₁, Р₀,

где:

Р₃=a₁XORa₂XORa₃XORa₄XORa₅XORa₆XORa₇;

Р₂=а₀XORa₄XORa₅XORa₆XORa₇;

Р₁=а₀XORa₂XORa₃XORa₆XORa₇;

Р₀=а₀XORa₁XORa₃XORa₅XORa₇.

В соответствии со вторым вариантом реализации данного изобретения внутренний код (12, 8, 3) сформирован из двух сокращенных блочных последовательностей. Первая последовательность блочного кода сформирована из подмножества, состоящего из восьми информационных бит, и из контрольного бита четности. Вторая последовательность блочного кода формируется из остальных информационных бит и трех контрольных бит четности. Сокращенный двоичный блочный код формируется в виде последовательности - как из первой последовательности блочного кода, так и из первой последовательности блочного кода в сочетании со второй последовательностью блочного кода. В обоих вариантах реализации сокращенный блочный внутренний код может декодироваться программно.

В режиме декодирования информация поступает с демодулятора на внутренний декодер, который производит декодирование принятого внутреннего кода, как описано более подробно ниже, далее декодер PC производит декодирование внешнего кода.

Декодирование внутреннего кода происходит следующим образом. Принятое кодовое слово прибавляется к половине потенциальных кодовых слов, тем самым образуя 128 параллельных сложений. Набор кодовых слов С_i={С₀...С₁₂₇} выбирается таким образом, что С_i+[1,1,1,1,1,1,1,1,1,1,1,1] равно полному набору кодовых слов. Далее производится 127 сравнений в соответствии с логической схемой. То есть, если |a|>|b|, то с равно а и состояние равно 1. Иначе с равно b и состояние равно 0,

где:

а и b - входные данные схемы сравнения;

с - результат сравнения.

Процесс прослеживается назад через дерево, чтобы определить наилучшую оценку Ci (0≤i≤127). Далее проверяется знак результата схемы сравнения. Если знак отрицательный, Cbest=Ci+[1,1,1,1,1,1,1,1,1,1,1,1]. Иначе Cbest равно Ci. Затем происходит обращение к таблице поиска для определения сообщения, соответствующего Ci.

Для систем передачи информации важной характеристикой является информационная надежность, под которой понимается способность системы передавать информацию с заданной достоверностью, то есть степенью соответствия принятого сообщения переданному. Упомянутая система использует в качестве внутреннего кода короткий двоичный код, исправляющий однократные ошибки. Данный код исправляет однократные ошибки, но если в принятых словах появятся две или более ошибок, то декодер не сможет декодировать данные слова, что приведет к появлению ошибочных и стертых символов в кодовых словах внешнего кода. Внешний код - код Рида-Соломона с минимальным расстоянием d позволяет декодировать любую конфигурацию, содержащую ν ошибок p стираний, при условии что:

В случае невыполнения неравенства (1) PC декодер не сможет правильно декодировать информационную последовательность. Это приведет к потере информации, что недопустимо в системе передачи данных без обратной связи.

Задачей изобретения является повышение вероятности правильного декодирования информации за счет восстановления стертых кодовых слов внутреннего кода.

Для этого в системах передачи данных, у которых на передающей стороне осуществляют кодирование информации внешним кодом Рида-Соломона и внутренним кодом, а на приемной стороне - декодирование с обнаружением и исправлением ошибок, выполняют следующие операции. На передающей стороне к блоку исходной информации добавляют циклическую контрольную сумму, полученный блок кодируют внешним кодом и затем внутренним кодом, в качестве которого используют расширенный код Голея, позволяющий исправлять все векторы ошибок веса 3 или меньшего. Расширенный код Голея в силу своего свойства квазисовершенности дает возможность исправлять ошибки веса 4. Затем на приемной стороне производят декодирование принятого блока информации, при этом сначала выполняют декодирование внутреннего кода, запоминают последовательность декодированных и стертых кодовых слов внутреннего кода в первом массиве и последовательность некорректируемых кодовых слов внутреннего кода во втором массиве. Далее осуществляют декодирование внешнего кода последовательности первого массива, в отношении которой выполняют вычисление и проверку циклической контрольной суммы. В случае положительного результата информацию отдают получателю сообщений, а в случае отрицательного результата производят восстановление стертых слов внутреннего кода последовательности первого массива. Для этого по заранее созданной таблице находят для каждого некорректируемого кодового слова внутреннего кода второго массива по шесть кандидатов и дополняют ими второй массив, затем для каждого некорректируемого кодового слова внутреннего кода второго массива производят выбор кандидата во втором массиве. Заменяют стертые кодовые слова внутреннего кода первого массива выбранными кандидатами, после чего повторяют декодирование внешнего кода вновь полученной последовательности первого массива. Процедуры восстановления стертых слов внутреннего кода и декодирования внешнего кода повторяют до тех пор, пока проверка циклической контрольной суммы не даст положительный результат.

Техническим результатом, достигаемым при решении поставленной задачи, является повышение достоверности принятого сообщения.

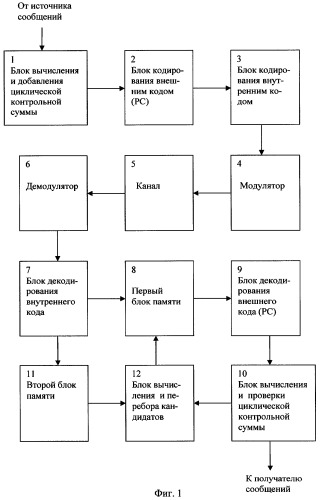
Указанная задача может быть решена с помощью системы кодирования-декодирования информации, которая состоит из последовательно соединенных блока вычисления и добавления циклической контрольной суммы 1, блока кодирования информации внешним кодом (PC) 2, блока кодирования внутренним кодом 3, модулятора 4, канала связи 5, демодулятора 6, блока декодирования внутреннего кода 7, первого блока памяти 8, блока декодирования внешнего кода (PC) 9, блока вычисления и проверки циклической контрольной суммы 10. При этом второй выход блока декодирования внутреннего кода 7 через второй блок памяти 11 соединен с первым входом блока 12 вычисления и перебора кандидатов, второй вход которого соединен со вторым выходом блока 10 вычисления и проверки циклической контрольной суммы, а выход блока 12 подключен ко второму входу первого блока памяти 8.

Предлагаемая система обеспечивает кодирование информации каскадным кодом, состоящим из двух кодов - внутреннего (n, k) и внешнего (N, K), где n и N - общее число символов; k и K - число информационных символов в комбинации внутреннего и внешнего кодов соответственно.

В качестве внутреннего кода используется расширенный код Голея (24, 12, 8), являющийся квазисовершенным кодом ([3], стр. 142). Это означает, что все сферы радиуса r, равные 3, вокруг кодовых слов (то есть множества всех слов на расстоянии Хэмминга r от кодовых слов) не пересекаются, но каждое из слов находится на расстоянии, не превышающем (r+1), хотя бы от одного кодового слова. Данный код позволяет исправлять все векторы ошибок веса 3 или меньшего и в силу своего свойства квазисовершенности он дает возможность исправлять ошибки веса 4. Ошибки веса, большего или равного 5, не исправляются никогда. Вследствие чего в известной системе используют код Голея с характеристиками (24, 12, 8), а ошибки веса 4 исправляют с помощью перебора кодовых слов, находящихся на расстоянии Хэмминга, равном 4, от ошибочного кодового слова.

В качестве внешнего кода используют недвоичные коды, например коды Рида-Соломона (PC) над полем GF (2^m),

где m - расширение двоичного поля (см. [3], стр. 201).

В качестве примера в предлагаемой системе используют внешний код PC (255, K, D) над полем GF(2⁸).

Для вычисления циклической контрольной суммы в предлагаемой системе используют алгоритм циклических избыточных кодов - Cyclic Redundancy Codes (CRC). Этот алгоритм представляет собой высокоэффективное средство обнаружения ошибок. Благодаря вычислению циклической контрольной суммы возможно определение искажений данных, так как изменение данных приводит к изменению циклической контрольной суммы. Основным свойством алгоритма является то, что циклическая контрольная сумма изменяется как при искажении одного, так и более битов информационной последовательности. В качестве примера в предлагаемой системе используют алгоритм CRC-32 [11], что означает применение 32-битного порождающего полинома

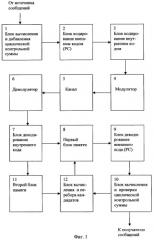
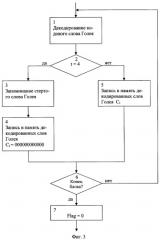
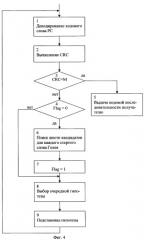
На фиг.1 представлена функциональная схема системы, реализующей предложенный способ. На фиг.2 - процесс преобразования информации (цифрами 1-7 обозначены операции процесса кодирования сообщения, цифрами 1'-5' обозначены операции восстановления сообщения на приемной стороне). На фиг.3 - укрупненная блок-схема алгоритма декодирования информации, закодированной внутренним кодом. На фиг.4 - укрупненная блок-схема алгоритма декодирования внешнего кода.

Операции кодирования и декодирования информации внешним (недвоичным) кодом - кодом PC осуществляют программно. Процессы кодирования и декодирования кодов PC можно выполнять, например, с помощью алгоритмов, основанных на спектральных методах, а именно декодирующим алгоритмом Берлекэмпа-Месси с возможностью исправления стираний. Данный алгоритм подробно описан в многочисленных учебниках и публикациях (например, в [3], стр. 285).

Операции кодирования и декодирования информации внутренним кодом также осуществляют программно. Декодирование производят, например, с помощью декодера Меггита для кода Голея, который подробно описан (см. [3], стр. 183).

Для уменьшения вероятности ложного набора при вычислении циклической контрольной суммы используют алгоритм CRC-32, применяемый последовательно два раза, что означает получение 64-битного остатка.

Расчет вероятностных характеристик показывает преимущество данного способа над другими подобными. Нижеприведенные расчеты основаны на теории вероятности и комбинаторики. Количество переборов кандидатов для замены стираний зависит от количества стертых слов n_ст внутреннего кода, в данном случае - 6^nст. Среднее число стертых кодовых слов во всей последовательности из 170 кодовых слов внутреннего кода определяют по формуле:

где:

где:

P_ош/бит - вероятность ошибки на бит сообщения для реальных коротковолновых (KB) каналов (на практике равна 0,04-0,07);

С - число сочетаний 4-х из 24-х.

Пусть Р_ош/бит равно 0,05, тогда Р{4 ошибки в слове} равно 0,0238, а n_ст приблизительно равно 5. Это означает что максимальное количество переборов кодовых слов внутреннего кода 6⁵ равно 7776, что вполне осуществимо на современных вычислительных машинах.

Вероятности присутствия двух, пяти, восьми стертых кодовых слов в последовательности внутреннего кода определяют по формуле:

Р{4 ошибки в слове} равно 0,0238, следовательно, Р{2 стертых слова} равно 0,1423, Р{5 стертых слов} равно 0,1599, Р{8 стертых слов} равно 0,0304.

Так как для вычисления циклической контрольной суммы используют алгоритм CRC-32, применяемый последовательно два раза, что означает получение 64-битного остатка, то вероятность ложного набора Р_лн составит 2^-64, что приблизительно равно 5,421·10^-20.

Вероятность ложного набора при количестве переборов N определяют по формуле:

где (1-Р_лн)^N - вероятность отсутствия ложного набора при N переборах.

В случае, если в последовательности внутреннего кода присутствуют пять стертых кодовых слов, то максимальное количество переборов составит 6⁵, то есть 7776. Следовательно, вероятность ложного набора Р_лн(6⁵) равна 4,215·10^-16. Если в последовательности внутреннего кода будут присутствовать больше пяти стертых кодовых слов, то максимальное количество переборов будет резко возрастать, а с ним и вероятность ложного набора Р_лн(N). И если среднее число стертых кодовых слов во всей последовательности будет больше пяти, то вероятность ложного набора Р_лн(N) станет недопустимо большой. В этой ситуации ее можно понизить с помощью увеличения количества разрядов циклической контрольной суммы при применении порождающего полинома большей степени.

Вероятности ложного набора Р_лн (N) при присутствии пяти, шести, семи, восьми стертых кодовых слов в последовательности внутреннего кода: Р_лн(6⁵) равна 4,215·10^-16, Р_лн(6⁶) равна 2,529·10^-15, Р_лн(6⁷) равна 1,517·10^-14, Р_лн(6⁸) равна 1,091·10^-13.

Вероятность ошибочного декодирования сообщения определяют по следующей формуле:

где:

D - конструктивное расстояние внешнего кода;

Р_{ош/симв} - вероятность ошибки символа внешнего кода.

где:

Р_{ош/Голея} - вероятность ошибки кодового слова Голея, которую определяют по формуле:

1) в случае, если перебор кодовых слов внутреннего кода не применяют:

2) в случае, если перебор кодовых слов внутреннего кода применяют:

Таким образом, при использовании кода Рида-Соломона (255, 235, 21), вероятности ошибки в канале на бит сообщения Р_ош/бит, равной 0,05, количестве стертых кодовых слов Голея n_ст, равном пяти, и вероятности ложного набора Р_лн, равной 4,215·10^-16, вероятность ошибочного декодирования блока кодовой последовательности Р_ош равна 0,0000000099. Для сравнения, при тех же параметрах, но без восстановления стертых кодовых слов внутреннего кода вероятность ошибочного декодирования сообщения Р_ош равна 0,0144087. Следовательно, такое сочетание методов кодирования и декодирования позволило существенно повысить вероятность правильного декодирования информации и тем самым решить задачу изобретения, а именно повысить достоверность принятого сообщения.

Предложенный способ в системах передачи данных, преимущественно без обратной связи, осуществляют следующим образом (фиг.1). На передающей стороне к блоку исходной информации, поступающему от источника сообщений, добавляют циклическую контрольную сумму. Затем полученный блок (блок исходной информации вместе с добавленной к нему циклической контрольной суммой) кодируют внешним кодом PC и затем внутренним кодом. Далее закодированный блок модулируют и передают в канал. После демодулятора принятый блок информации декодируют внутренним кодом. Последовательность декодированных и стертых кодовых слов внутреннего кода запоминают в первом массиве (с помощью первого блока памяти 8). Если декодирование кодового слова внутреннего кода невозможно, то это некорректируемое кодовое слово сохраняют во втором массиве (с помощью второго блока памяти 11), а в первый блок памяти записывают вместо него стертое кодовое слово в виде двенадцати нулей. Далее декодируют внешний код PC последовательности декодированных и стертых кодовых слов внутреннего кода. Затем вычисляют и проверяют циклическую контрольную сумму упомянутой информационной последовательности. При положительном результате проверки CRC информацию выдают получателю сообщений. При отрицательном результате проверки производят восстановление стертых слов внутреннего кода последовательности первого массива. Операции восстановления стертых слов внутреннего кода и декодирования внешнего кода повторяют до тех пор, пока проверка CRC не даст положительный результат.

В процессе передачи сообщения от источника к потребителю исходное сообщение трансформируют в различные формы, удобные для той или иной операции (фиг.2). Последовательность преобразований, происходящих с исходным сообщением в процессе операций кодирования и декодирования, можно представить следующим образом.

При кодировании информации:

1) Формируют блок исходной информации. Он будет представлен в виде двоичной последовательности из N бит:

α₀, α₁, α₂, ..., α_N-1.

2) Вводят первую избыточность данных в виде m бит циклической контрольной суммы. Таким образом, блок исходной информации будет представлен в виде двоичной последовательности из N+m бит:

α₀, α₁, α₂, ..., α_N-1, α_N, α_N+1, α_N+2, ..., α_N+m-1.

3) Разбивают блок исходной информации на блоки по 8 бит (поскольку кодирование производят по принципу каскадного кодирования, внешним кодом которого является код Рида-Соломона, определенный над полем GF(2⁸)):

α₀, α₁, ..., α₇, α₈, α₉, ...,α₁₅,......, α_N+m-9, α_N+m-8, ..., α_N+m-1.

То есть получают новую двоичную последовательность a₀, a₁, ..., a_(N+m)/8-1, каждый символ которой является элементом поля GF(2⁸). Данную двоичную последовательность используют как исходную для внешнего кода.

4) Кодируют данную последовательность кодом Рида-Соломона с характеристиками (255, K, D),

где:

K=(N+m)/8;

D=255-K+1.

Таким способом вводят избыточность и двоичную последовательность представляют в виде 255 элементов поля GF(2⁸), каждый из которых по 8 бит:

b₀, b₁, ..., b₂₅₄.

5) Последовательность из 255 элементов по 8 бит разбивают на символы над полем GF(2¹²), то есть на 170 элементов по 12 бит (так как в качестве внутреннего кода каскадного кода используют код Голея с характеристиками (24, 12, 8), а количество информационных символов данного кода равняется 12):

где:

b_i ¹ - первые 4 бита элемента b_i;

b_i ² - вторые 4 бита b_i.

Преобразованную последовательность используют как исходную для внутреннего кода.

6) Полученную последовательность поэлементно кодируют кодом Голея с характеристиками (24, 12, 8). В итоге двоичную последовательность представляют в виде 170 элементов, каждый из которых содержит по 24 бита:

d₀, d₁, ..., d₁₆₉.

7) Закодированную последовательность подают на модулятор, где ее преобразуют в последовательность сигналов, которую отправляют в канал.

Процесс восстановления сообщения на приемной стороне системы передачи информации производят в обратном порядке, а именно:

1') Преобразуют принятый сигнал в последовательность кодовых слов для внутреннего декодера (170×24 бита):

d₀, d₁, ..., d₁₆₉.

2') Декодируют код Голея. Последовательность принимает вид 170 блоков по 12 бит:

γ₀, γ₁, ...γ₁₆₉.

3') Преобразуют последовательность для внешнего декодера (255×8 бит):

b₀, b₁, ..., b₂₅₄.

4') Декодируют код Рида-Соломона. Последовательность принимает вид 170 блоков по 8 бит:

α₀, α₁, ..., α₁₆₉.

5') Вычисляют и проверяют циклическую контрольную сумму. Если проверка даст положительный результат, то полученное сообщение совпадет с переданным и его отправят получателю.

Алгоритм декодирования внутреннего кода включает следующую последовательность действий (фиг.3). От демодулятора принятое кодовое слово передают на декодер Голея (операция 1), в котором происходит декодирование кодового слова Голея. Внутренним кодом является код Голея (24, 12, 8), минимальное кодовое расстояние данного кода d равно восьми, а значит декодер может исправить не более трех ошибок. Если в кодовом слове Голея было четыре ошибки, то правильное декодирование такого слова будет невозможно, вследствие чего появятся стертые слова кода Голея. При выполнении операции 2 проверяют количество ошибочных бит t в декодируемом кодовом слове. Если t не равно четырем, то при выполнении операции 5 декодированное кодовое слово С_i записывают в первый блок памяти, где хранят массив декодированных кодовых слов внутреннего кода. Если t равно четырем, то принятое кодовое слово при выполнении операции 3 записывают во второй блок памяти, где хранят массив некорректируемых кодовых слов Голея, и при выполнении операции 4 производят запись стертого кодового слова в виде двенадцати нулей (С_i равно 000000000000) вместо декодируемого кодового слова в первый блок памяти, где хранят массив декодированных кодовых слов внутреннего кода. Если принятый блок закодированной информации не закончился, что проверяют при выполнении операции 6, то производят переход к следующему принятому кодовому слову Голея и повторяют процедуру декодирования, начиная процесс с выполнения операции 1. В противном случае при выполнении операции 7 переменной Flag будет присвоено значение 0 и произойдет переход к декодированию внешнего кода.

Алгоритм декодирования внешнего кода включает следующую последовательность действий (см. фиг.4). При выполнении операции 8 декодируют кодовые слова PC, определенного над полем GF(2⁸), которые хранят в первом блоке памяти, где находится массив декодированных кодовых слов внутреннего кода. В начале процесса декодирования, когда переменная Flag=0, кодовое слово может содержать стертые символы, то есть символы, двоичное представление которых имеет вид 00000000. Следовательно, данную информационную последовательность необходимо декодировать декодером PC с возможностью восстановления стираний. При выполнении операции 9 производят вычисление циклической контрольной суммы (CRC) декодируемой информации. При выполнении операции 10 результат вычисления сравнивают с остатком информационной последовательности, содержащей циклическую контрольную сумму М. Если CRC равно М, то при выполнении операции 12 декодированную информацию отдают получателю сообщений. В противном случае при выполнении операции 11 проверяют значение переменной Flag. Если Flag равна 0, то восстановление стертых кодовых слов Голея не производилось. Следовательно, необходимо определить кандидатов для замены стертых кодовых слов Голея (операция 13). Определение кандидатов производят по таблице, содержащей 4096 кодовых слов Голея и, кроме того, по шесть кодовых слов для каждого кодового слова Голея, находящихся на расстоянии Хемминга, равном четырем, от соответствующего кодового слова Голея. Эти шесть кодовых слов являются кандидатами для замены соответствующего кодового слова. Поиск по таблице производят с помощью кодовых слов, хранящихся во втором блоке памяти, который содержит массив некорректируемых кодовых слов Голея. В итоге для каждого некорректируемого кодового слова Голея находят шесть кандидатов для замены и формируют массив кандидатов. При выполнении операции 14 переменной Flag присваивают значение 1 и поиск кандидатов для данного блока информации больше не производят. Если при выполнении операции 4 Flag равна 1, то происходит переход к операции 15 - выбору очередной гипотезы с помощью простого перебора кандидатов в массиве кандидатов для каждого некорректируемого кодового слова Голея. Далее при выполнении операции 16 выбранную гипотезу записывают в первый блок памяти, где хранят массив декодированных кодовых слов внутреннего кода. То есть каждый кандидат, соответствующий некорректируемому кодовому слову Голея, будет записан в память вместо стертого кодового слова и затем переходят к выполнению операции 8. Декодирование кодового слова PC производят до тех пор, пока при выполнении операции 10 CRC не будет равна остатку информационной последовательности, содержащему циклическую контрольную сумму. Следовательно, принятая кодовая последовательность будет полностью декодирована.

Таким образом можно констатировать, что особенно эффективным является применение каскадного кодирования с восстановлением стертых кодовых слов внутреннего кода, которое позволило достичь вероятности ошибочного декодирования сообщения Р_ош, равной 0,0000000099 (при использовании в качестве внешнего кода - кода Рида-Соломона (255, 235, 21), вероятности ошибки в канале на бит сообщения Р_ош/бит, равной 0,05, количестве стертых кодовых слов Голея, равном пяти, и вероятности ложного набора Р_лн, равной 4,215·10^-16). Для сравнения, при тех же параметрах, но без восстановления стертых кодовых слов внутреннего кода, вероятность ошибочного декодирования сообщения Р_ош равна 0,0144087. Тем самым решена задача изобретения, то есть повышена вероятность правильного декодирования информации и достоверность принятого сообщения.

Источники информации

1. Патент US 5996103.

2. Патент US 6374382.

3. Блейхут Р. "Теория и практика кодов, контролирующих ошибки". М.: Мир, 1986.

4. Форни Д. "Каскадные коды". М.: Мир, 1970.

5. Дж. Кларк мл., Дж. Кейм. "Кодирование с исправлением ошибок в системах цифровой связи". М.: Радио и связь, 1986.

6. Истомин Г.С., Парижская И.С. "Об использовании микро-ЭВМ для реализации арифметических операций в полях Галуа". Техника средств связи, серия ТПС, вып.2, 1978.

8. Кузьмин И.В., Кедрус В.А. "Основы теории информации и кодирования". Киев: Вища школа, 1986.

9. Муттер В.М., Петров Г.А., Маринкин В.И., Степанов B.C. "Микропроцессорные кодеры и декодеры". М.: Радио и связь, 1991.

10. Чалсалл Ф. "Передача данных, сети компьютеров и взаимосвязь открытых систем". М.: Радио и связь, 1995.

11. Росс Н. Вильямс. "Элементарное руководство по CRC-алгоритмам обнаружения ошибок". FTP: ftp.adelaide.edu.au/pub/rocksoft/crc_v3.txt 1993.

Способ кодирования-декодирования информации в системах передачи данных, преимущественно без обратной связи, согласно которому на передающей стороне осуществляют кодирование информации внешним кодом Рида-Соломона в поле GF (q) (q - алфавит кода) и внутренним кодом, на приемной стороне - декодирование с обнаружением и исправлением ошибок, отличающийся тем, что на передающей стороне к блоку исходной информации добавляют циклическую контрольную сумму, полученный блок кодируют внешним кодом и затем внутренним кодом, в качестве которого используют расширенный код Голея, на приемной стороне производят декодирование принятого блока информации, при этом сначала выполняют декодирование внутреннего кода, запоминают последовательность декодированных кодовых слов в массиве декодированных кодов слов внутреннего кода, запоминают последовательность некорректируемых кодовых слов в массиве некорректируемых кодовых слов внутреннего кода, при этом одновременно запоминают последовательность стертых кодовых слов вместо некорректируемых кодовых слов в массиве декодированных кодовых слов внутреннего кода, далее осуществляют декодирование внешнего кода последовательности декодированных кодовых слов массива декодированных кодовых слов внутреннего кода, в отношении которой выполняют вычисление и проверку циклической контрольной суммы, и в случае положительного результата информацию отдают получателю сообщений, а в случае отрицательного результата производят восстановление последовательности стертых слов массива декодированных кодовых слов внутреннего кода, при этом по заранее созданной таблице, включающей все кодовые слова Голея и по шесть дополнительных кодовых слов для каждого кодового слова Голея, находящихся на расстоянии Хемминга равном четырем от соответствующего кодового слова Голея, определяют для каждого некорректируемого кодового слова шесть дополнительных кодовых слова, и дополняют ими массив некорректируемых кодовых слов внутреннего кода, затем для каждого некорректируемого кодового слова массива некорректируемых кодовых слов внутреннего кода производят выбор дополнительного кодового слова из шести дополнительных кодовых слов, заменяют стертые кодовые слова массива декодированных кодов слов внутреннего кода выбранными дополнительными кодовыми словами массива некорректируемых кодовых слов внутреннего кода, а восстановление стертых слов внутреннего кода и декодирование внешнего кода повторяют до тех пор, пока проверка циклической контрольной суммы не даст положительный результат.