Линейная коррекция на основе преобразования фурье для нисходящей линии связи мдкр

Линейная коррекция на основе преобразования фурье для нисходящей линии связи мдкр

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к способу приема в системах мобильной телефонной связи МДКР, в которых принятый сигнал отделяется от других помеховых сигналов посредством алгоритма линейной коррекции, который позволяет избегать обращения матрицы.

Предпосылки изобретения

Основной проблемой при разработке и реализации системы передачи данных являются одновременная передача и прием сигналов от нескольких одновременно активных пользователей при минимальных взаимных помехах. Ввиду этого и используемой производительности при передаче используются различные протоколы передачи и методы множественного доступа, причем в мобильной телефонной связи чаще всего используются МДЧР (множественный доступ с частотным разделением) и МДВР (множественный доступ с временным разделением), а в последнее время и МДКР (множественный доступ с кодовым разделением).

МДКР - это метод множественного доступа, основанный на технике расширения по спектру, и с недавних пор используется в системах сотовой радиосвязи наряду с ранее использовавшимися МДЧР и МДВР. МДКР имеет много преимуществ над предыдущими методами, в частности, простота распределения частот и спектральная эффективность.

Согласно методу МДКР, узкополосный сигнал данных пользователя расширяется до сравнительно широкой полосы путем умножения на код расширения, имеющий гораздо более широкую полосу, чем сигнал данных. Ширина полосы, используемая в известных тестовых системах, принимает значение, например, 1,25 МГц, 10 МГц и 25 МГц. Умножение расширяет сигнал данных на всю используемую полосу. Все пользователи одновременно осуществляют передачу в одной и той же полосе частот. В каждом соединении между базовой станцией и мобильной станцией используется отдельный код расширения, и сигналы пользователей можно отличать друг от друга на приемниках на основании кода расширения пользователя. По возможности, коды расширения выбирают таким образом, чтобы они были взаимно ортогональными, т.е. не коррелировали друг с другом.

Корреляторы в традиционно реализуемых приемниках МДКР синхронизируются с полезным сигналом, который они распознают на основании кода расширения. В приемнике сигнал данных восстанавливается до исходной полосы путем умножения на тот же код расширения, что и на этапе передачи. В идеале, сигналы, умноженные на другой код расширения, не коррелируют и не восстанавливаются в узкую полосу. По отношению к полезному сигналу они представляют собой шум. Задача состоит в том, чтобы детектировать сигнал нужного пользователя из ряда помеховых сигналов. На практике коды расширения в некоторой степени коррелируют, и сигналы других пользователей затрудняют детектирование полезного сигнала, искажая принятый сигнал. Эта взаимная помеха, создаваемая пользователями друг другу, называется помехой множественного доступа.

Ситуация особенно проблематична, когда один или несколько пользователей осуществляют передачу со значительно более высоким уровнем сигнала, чем другие пользователи. Эти пользователи, использующие более высокий уровень сигнала, создают значительные помехи соединениям других пользователей. Такая ситуация называется проблемой «ближней-дальней зоны» и может возникать, например, в системах сотовой радиосвязи, когда один или несколько пользователей находятся вблизи базовой станции, а некоторые пользователи удалены от нее, вследствие чего пользователи, находящиеся ближе, забивают сигналы других пользователей в приемнике базовой станции, если система не использует быстродействующих и высокоэффективных алгоритмов управления мощностью.

Особенно проблематичен прием сигналов в асинхронных системах, т.е. системах, где сигналы пользователей не синхронизированы друг с другом, поскольку символы одних пользователей искажаются символами других пользователей. Однако в традиционных приемниках фильтры, согласованные с кодами расширения, и скользящие корреляторы, используемые в качестве обнаружителей, не обеспечивают хорошую работу в ситуациях «ближней-дальней зоны». Из известных методов наилучший результат дает декоррелирующий обнаружитель, который исключает помеху множественного доступа из принятого сигнала, умножая его на кросс-корреляционную матрицу используемых кодов расширения. Декоррелирующий обнаружитель подробно описан в статье Lupas, Verdu, 'Linear multiuser detectors for synchronous code-division multiple access channels', IEEE Transactions on Information Theory, т. 35, №1, стр. 123-126, янв. 1989 г.; и Lupas, Verdu, "Near-far resistance of multiuser detectors in asynchronous channels", IEEE Transactions on Communications, т. 38, апр. 1990 г., однако эти методы предусматривают выполнение многих операций, например операций обращения матрицы, которые требуют высоких вычислительных затрат и особенно критичны, когда качество канала связи и количество пользователей постоянно изменяются, как, например, в системах сотовой радиосвязи.

Канальная коррекция является эффективным средством улучшения показателей приемника нисходящей линии связи в частотно-избирательной нисходящей линии связи МДКР. Современные исследования охватывают два типа линейной коррекции, а именно неадаптивную линейную коррекцию и адаптивную линейную коррекцию. Неадаптивные линейные корректоры обычно предполагают «кусочную» стационарность канала и проектирование корректора согласно некоторым критериям оптимизации, таких как МСКО (минимальная среднеквадратическая ошибка) или сведение к нулю, что в общем случае ведет к решению системы линейных уравнений путем обращения матрицы. Это требует большого объема вычислений, в особенности, когда время когерентности канала мало, и требуется частое обновление корректоров. С другой стороны, адаптивные алгоритмы решают аналогичные проблемы оптимизации на основе МСКО или сведение к нулю с применением стохастических градиентных алгоритмов, избегая прямого обращения матрицы. Хотя адаптивные алгоритмы легче выполнять, они менее надежны, поскольку их сходимость и производительность зависят от выбора параметров, например размера шага.

С точки зрения уровня техники, требуется процедура коррекции, которая отличается надежностью и не связана с большим объемом вычислительной мощности.

Сущность изобретения

Задачей настоящего изобретения является обеспечение способа коррекции для сигналов нисходящей линии связи МДКР, который позволяет избегать обращения матрицы, требующего большого объема вычислений.

Признаком изобретения является процесс линейной фильтрации, в котором на этапах процесса генерации коэффициентов фильтра используются только БПФ и ОБПФ.

Признаком изобретения является аппроксимация корреляционной матрицы циркулянтной матрицей, которая диагонализируется посредством операции ДПФ.

Краткое описание чертежей

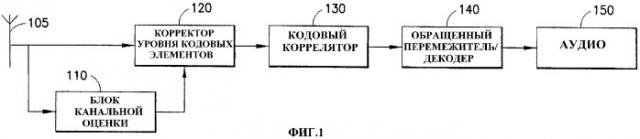
Фиг.1 - блок-схема приемника, отвечающего изобретению.

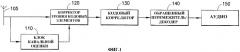
Фиг.2 - схема процесса коррекции с использованием интерпретации частотной области.

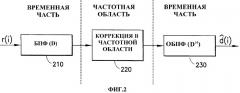
Фиг.3 - результат численного моделирования метрики ошибок для альтернативных процессов.

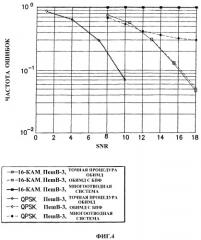
Фиг.4 - сравнение процесса, отвечающего изобретению, и точного решения по частоте ошибок.

Фиг.5 - сравнение с фиг.4 для другого варианта осуществления.

Фиг.6 - эффект включения многоканального разнесения.

Фиг.7 - частота ошибок для альтернативного варианта осуществления.

Фиг.8, a, b - различные уравнения, используемые в анализе в соответствии с изобретением.

Предпочтительные варианты осуществления изобретения

В случае нисходящей линии связи МДКР с J активными пользователями, каждому из которых присвоено число K_j кодов для j=1.. J. Пусть K - полное количество активных кодов расширения (суммируемых по J). Заметим, что в нашем рассмотрении мы используем индекс кода расширения, а не индекс пользователя для упрощения записи. В передатчике выражение для сигнала на уровне кодовых элементов задано Ур.(1) на фиг.8, где i, m и k - индексы кодового элемента, символа и кода расширения. Код скремблирования базовой станции обозначается c(i). При этом a_k обозначает мощность, назначенную коду расширения k, bk - это последовательность информационных символов для кода расширения k, и s_k(i) - это код расширения k.

Пусть h=[h₀;:::h_L] - составной вектор канального импульса на уровне кодовых элементов для кода расширения k. Заметим, что h включает в себя вклады от передающего формирователя импульсов, беспроводного канала распространения и приемного фильтра, поэтому он будет изменяться в соответствии с изменениями среды. Заметим также, что, поскольку в данном описании рассматривается только код расширения k, то для ясности вместо h_k используется h. Матрично-векторное выражение для принятого сигнала задано Ур.(2) на фиг.8. Для облегчения рассмотрения линейной коррекции F+1 кодовых элементов упорядочиваются в принятом векторе r так, что r(i)=[r(i+F);:::; r(i);:::; r(i-F)]^r=H(i)d(i) + n(i), где d(i)=E[d(i)d^H(i)] - мощность переданного кодового элемента, и h(i) - (F+1)-й столбец в H(i). Решение в таком виде нежелательно, поскольку зависит от индекса i кодового элемента и изменяется во времени. Однако зависимость от i можно устранить, если принять следующие два предположения.

а) Канальный вектор h(i) является стационарным на большом блоке кодовых элементов. Это условие удовлетворяется при выборе такого размера блока, чтобы временная протяженность блока составляла малую часть времени когерентности канала. При этом условии зависимость от i устраняется из h(i) и H(i).

b) Переданный сигнал d(i) на уровне кодовых элементов является белым и стационарным в широком смысле. Можно показать, что это условие строго выполняется, если система полностью нагружена, т.е. когда K=G, и каждому коду расширения назначена одна и та же мощность. В противном случае это условие выполняется довольно хорошо за исключением случаев слабонагруженных систем, т.е. когда K<<G. Таким образом, следующее решение является неочевидным, поскольку получается, что малое отношение сигнал/шум лучше, чем традиционно «лучшее» условие, когда сигнал отчетливо выделяется над фоном.

В результате устранения зависимости от времени получаем Ур.(4) на фиг.8 в качестве решения для вектора w фильтра, где сигма это константа, выражающая передаваемую мощность, и R - корреляционная матрица из Ур. (3). Специалистам в данной области понятно, что оценочные данные после коррекции выражаются как d(i)=w^Hr(i), где r - принятый сигнал в Ур.(2), и w изменяется сравнительно медленно. Выяснилось, как показано в Ур.(5), что R имеет вид ленточной матрицы Теплица, отдельные элементы которой, заданные посредством Ур.(6), зависят от вектора h канального импульса и некоторых констант.

Специалистам в данной области известно, что аналитическое решение для w в отношении предыдущей проблемы (выражение w через другие наблюдаемые параметры) требует обращения корреляционной матрицы R. Для вычисления обратной матрицы необходимы вычислительные ресурсы и время. В мобильном телефоне трудно обеспечить вычислительные ресурсы, необходимые для обеспечения удовлетворительного решения, поскольку ограниченные аппаратные ресурсы не позволяют достаточно быстро производить вычисления. Таким образом, изобретение хорошо приспособлено к использованию в приемнике мобильного телефона в системе сотовой связи МДКР.

Сложность обращения матрицы имеет порядок L_F ³, где L=2F+1 - длина фильтра. Кроме того, операция обращения матрицы может отличаться численной нестабильностью и неточностью в частых случаях реализаций с фиксированной точкой.

Преимущественным признаком изобретения является то, что можно избежать обращения матрицы благодаря процессу, в котором обращение матрицы заменяется преобразованиями Фурье. Согласно предпочтительному варианту осуществления изобретения, обращение корреляционной матрицы заменяется двумя БПФ (быстрыми преобразованиями Фурье) и обратным БПФ.

Если L_F>2L, то можно преобразовать R в циркулянтную матрицу S путем прибавления матрицы С согласно Ур.(7), где С - это верхняя треугольная «угловая» матрица, заданная в Ур.(8). Целью такой замены является получение преимущества того свойства, что каждую циркулянтную матрицу можно диагонализировать посредством матрицы ДПФ (дискретного преобразования Фурье), т.е. S=D^H(Λ)D, где D задано в Ур.(9), и Λ - диагональная матрица, полученная применением ДПФ к первому столбцу S.

Задавая V согласно Ур.(10), специалистам в данной области должно быть понятно, что проблема обращения матрицы R размером L_F×L_F свелась к обращению матрицы J_2L-VS^-1V^H размером 2Lx2L, где J_2L это «обменная» матрица размером 2Lx2L (из единиц на антидиагоналях).

Кроме того, если длина фильтра много больше длины канальной корреляции, т.е. L_F>>2L, то сложение двух углов в корреляционную матрицу R не приведет к значительному изменению собственной структуры матрицы. Соответственно, матрица, обратная R, приблизительно равна матрице, обратной S. Таким образом, прямое обращение матрицы не требуется, поскольку матрицу, обратную S, можно получить с помощью некоторых операций БПФ и ОБПФ.

Возвращаясь к проблеме выделения полезного сигнала, укажем, что решение принимает вид w=S^-1h=D^H(Λ)^-1Dh, где операции D и D^H представляют операции ДПФ и ОДПФ, которые можно заменить более простыми в вычислительном отношении операциями БПФ.

В этом случае процесс распознавания сигнала сводится к следующему:

1) оценка корреляционной матрицы R на основании принятого сигнала;

2) преобразование R в циркулянтную матрицу S путем прибавления двух угловых матриц;

3) выполнение БПФ(s), где s - первый столбец S и генерация Λ;

4) вычисление Dh=БПФ(h) и (Λ)^-1Dh, и

5) преобразование обратно во временную область,

где

w =D^H(Λ)^-1Dh=ОБПФ((Λ)^-1Dh);

6) применение полученного w к принятому вектору r для вычисления оценки d чипа.

Элементы величины (Λ)^-1Dh также будем называть отводами фильтра частотной области. Затем оценку d кодового элемента обрабатывают традиционным образом, чтобы генерировать аналоговый голосовой сигнал (или данные).

Поскольку фильтр не изменяется на протяжении блока из N кодовых элементов, то вычислительная нагрузка в расчете на один кодовый элемент нормализуется по N. N может быть равно в порядке иллюстрации 1024. Тогда общая сложность, приходящаяся на кодовый элемент, составляет порядка (L_F+(3L_F/2N)log2L_F), что выгоднее по сравнению со сложностью порядка (L_F+(1/N)L_F ³) для метода прямого обращения матрицы.

На фиг.1 показана блок-схема приемника, отвечающего изобретению в порядке иллюстрации мобильного телефона в системе сотовой связи МДКР, в котором антенна 105 принимает входные сигналы, которые поступают на блок 110 канальной оценки, который генерирует начальную оценку параметров, используемых при вычислениях, а также поступает на корректор 120, который представляет схемы, осуществляющие различные вычисления, рассмотренные ниже. В этом алгоритме процесс оценивания элементов корреляционной матрицы осуществляется согласно любому удобному традиционному методу, например, проиллюстрированному в книге Луиса Шарфа (Louis Scharf) и Эдисона Уэсли (Addison Wesley) "Statistical Signal Processing". Вычисления могут производиться в устройстве специального назначения, включающем в себя интегральную схему цифрового сигнального процессора, например микропроцессор. Инструкции по выполнению процесса могут храниться на любом удобном машиночитаемом носителе, например, в микросхеме постоянной памяти.

Функция корректора частично или полностью восстанавливает ортогональность отдельных кодов расширения, представляющих различные «каналы» для каждого пользователя.

После корректора традиционный кодовый коррелятор, известный специалистам в данной области, например описанный в книге Джона Проукиса (John Proakis) "Digital Communications", McGraw Hill, выделяет мощность, связанную с конкретным кодом, который несет нужные данные. Традиционный обращенный перемежитель выделяет конкретные нужные данные. Блок 150, обозначенный «Аудио», схематически представляет традиционные схемы, которые преобразуют цифровые сигналы, обработанные к этому моменту, в аналоговый аудиосигнал (или в случае передачи данных направляет данные на следующую ступень обработки). Для удобства выражения в формуле изобретения выходной сигнал обращенного перемежителя 140 назван просто «выходным сигналом», и процессы, представленные блоком 150 (суммирование блока данных, осуществление цифроаналоговой обработки, сглаживание, усиление и т.д.), названы обработкой выходного сигнала.

На фиг.2 показан подход к проблеме коррекции, который концептуально ясен, хотя он не обеспечивает вычислительных преимуществ предпочтительных вариантов осуществления. Блок 210 представляет преобразование Фурье, применяемое к каждому кодовому элементу, из временной области в частотную область. Блок 220 представляет вычисления коррекции, аналогичные рассмотренному выше процессу линейной коррекции, для вычисления матрицы, обратной Λ. Блок 230 представляет обратное преобразование Фурье обратно во временную область. Поскольку этот подход требует ДПФ для каждого кодового элемента, его сложность составляет порядка (L_F+(1/2)L_Flog2L_F+(L_F/N)log2L_F), что больше, чем обеспечивают другие подходы, хотя все еще благоприятно по сравнению с прямым обращением.

Численные методы вычислений

Было найдено два метода вычислений, повышающих точность используемой аппроксимации и стабильность результатов. Добавление искусственного уровня шума к матрице S путем прибавления единичной матрицы, умноженной на малую константу, предотвращает деление на малое число, когда собственные значения матрицы используются как делители в БПФ. Это эквивалентно предположению, что шум хуже, чем на самом деле.

Кроме того, поскольку длина вектора h импульса является константой, определенной профилем канала, можно повысить точность аппроксимации, увеличив длину фильтра L_F. Это приводит к снижению погрешностей, вносимых сложением в угловой матрице CL при вычислении собственных значений. Поскольку увеличение длины фильтра приводит к усложнению фильтра, лучшая альтернатива обеспечивается использованием вектора удвоенной длины (2L_F) при осуществлении вычислений в частотной области. Начальное множество кодовых элементов в принятом векторе расширяется до длины 2L_F. Этот расширенный вектор преобразуется в область Фурье и используется для вычислений. После обратного преобразования Фурье дополнительные L_F/2 отводов по обеим сторонам усекаются и используются только L_F отводов в центре.

На фиг.3 показано сравнение численного моделирования в системе широкополосного МДКР, усредненного по большому количеству блоков моделирования, квадрата разности между решением w прямого обращения матрицы и фильтра длиной L_F: J1=(Winv-WF)² и соответствующего квадрата разности расширенного фильтра, используемого в частотной области J2=(Winv-W2F)², где Winv это решение для w прямого обращения матрицы, WF - соответствующее решение из вышеописанного для фильтра длиной L_F, и W2F - соответствующее решение для фильтра длиной 2F в области Фурье. Можно видеть, что метод расширения обеспечивает значительно более низкие частоты ошибок. Увеличение частоты ошибок при более высоких отношениях сигнал/шум является следствием использования методов Фурье.

На фиг.4 и 5 приведены результаты моделирования для одного канала данных с использованием следующих параметров:

Таблица 1

Наименование параметра	Значение параметра
Полная мощность HS-DSCH	70 %
Мощность CPICH	10 %
Мощность SCH	10 % (выкл)
Несущая частота	2 ГГц
Коэффициент расширения HS-DSCH (канала данных)	16
Коэффициент расширения CPICH (пилот-канала)	256
Длина фильтра, LF	32
Оценка канала	идеальный

Под мощностью HS-DSCH понимается мощность, выделенная высокоскоростному совместно используемому каналу управления нисходящей линии связи, исчисляемая в процентном отношении к полной доступной мощности, выделенной базовой станции; мощность SCH это мощность, выделенная каналам синхронизации, которые включают в себя первичный канал синхронизации (P-SCH) и вторичный канал синхронизации (S-SCH). Мощность SCH делится поровну между P-SCH и S-SCH; и CPICH это общий пилот-канал.

Моделировались следующие три случая:

Таблица 2

	КФМн, ПешВ-3	16-КАМ, ПешВ-3	16-КАМ, АвтА-50
Модель канала	Пешеход B	Пешеход B	Автомобиль A
Скорость мобильной станции	3 км/ч	3 км/ч	50 км/ч
Скорость турбокодирования	0.6	0.5617	0.5617
Кол. кодов	10	8	8
Скорость передачи данных	2.8 Мбит/с	4.2 Мбит/с	4.2 Мбит/с

Многоканальное разнесение

Важным средством повышения рабочих характеристик приемника является прием с многоканальным разнесением. Прием с разнесением имеет два преимущества: во-первых, снижается вероятность простоя, поскольку вероятность глубокого замирания во всех каналах разнесения меньше; во-вторых, добавление каналов разнесения обеспечивает дополнительную размерность сигнала, которую можно использовать для повышения ОСШ, подавления МСП [межсимвольных помех] и ПМД [помех множественного доступа] и т.д.

Прием с многоканальным разнесением проявляется во многих формах. Помимо прочих, наиболее часто используются дискретизация с повышенной частотой, множество приемных антенн и поляризация антенны.

Осуществление этих методов зависит от статистической корреляции между разными каналами разнесения. В общем случае, чем меньше корреляция между разными каналами разнесения, тем лучше общая рабочая характеристика приемника.

В этом разделе метод линейной коррекции на основе БПФ распространен на системы, в которых используется прием с разнесением. Следующая обработка сходна для разных методов разнесения, поскольку все они математически выражаются одинаково. Итак, пусть М обозначает полное количество каналов разнесения (обычно 2 или 4), и модель принятого сигнала, выраженная Ур.(2), расширяется путем подстановки малого вектора h_i вместо скаляра h_i, используемого в предыдущем рассмотрении.

Корреляционная матрица вновь представляет собой ленточную блочную матрицу Теплица с той только разницей, что ее элементами теперь являются малые матрицы, что показано в Ур.(11) и (12). Задача решения матричного уравнения относительно вектора сигнала w усложняется, поскольку корреляционная матрица R теперь имеет размер ML_F×ML_F и соответственно ее труднее обратить напрямую.

После процедуры, описанной в предыдущем разделе, следует аппроксимирование блочной матрицы Теплица R блочно-циркулянтной матрицей S. Для обращения S мы вводим матрицу циклического сдвига Р согласно Ур.(13), где I - единичная матрица. Тогда S можно представить как Ур.(14), где символ ⊗ обозначает кронекерово произведение, и E_0.. E_LF-1 образуют первый «блочный» столбец в матрице S. Действуя по аналогии с предыдущим рассмотрением, P можно диагонализировать посредством ДПФ P=D^HWD, где D - матрица ДПФ, и W - диагональ формы W=diag(1, W_LF ^-1,.., W_LF ^-(LF-1)), где W_LF=e^j(api/LF). После некоторой подстановки S можно выразить как Ур.(15), где выражение (15-1) обозначает ОДПФ с учетом размерности, и выражение (15-3) выражает ДПФ с учетом размерности в том смысле, что ДПФ или ОДПФ применяется к каждому из М измерений разнесения. Среднее выражение (15-2) представляет собой блочно-диагональную матрицу, диагональные блоки которой являются элементными ДПФ массива матриц E₀,..., E_LF-1, выраженного в Ур.(16), где F является матрицей размера E₀,..., E_LF-1, заданной Ур.(17). Таким образом, матрица, обратная S, задается Ур.(18). Обращение F сводится к обращению L_F малых матриц размера MxM, поскольку F является блочно-диагональной.

Процедуру для многомерной передачи можно подытожить следующим образом:

1) оценка корреляционной матрицы R на основании принятого сигнала;

2) преобразование к блочно-циркулянтной матрице S путем прибавления двух «углов»;

3) выполнение «элементного» БПФ над первым «блочным» столбцом S и формирование F, обращение и получение F^-1;

4) вычисление БПФ для размерностей разнесения от h или (D⊗I)h и F^-1(D⊗I)h;

5) вычисление ОБПФ для размерностей разнесения от F^-1(D⊗I), чтобы получить весовой вектор w=(D⊗I)F^-1(D⊗I)h.

Этот алгоритм предусматривает одно БПФ для размерностей разнесения и ОБПФ над вектором размера ML_F×1 (эквивалентное M БПФ/ОБПФ длины L_F), одно «элементное» БПФ над матрицей размера MxM (что эквивалентно M² БПФ длиной L_F) и L_F обращений матрицы размером MxM. Сложность этого алгоритма составляет порядка (L_FM³+(M²+2M)/2L_Flog2L_F) по сравнению со значительно более высокой сложностью порядка (ML_F)³ прямого обращения матрицы R.

Результаты моделирования с использованием тех же параметров, что и прежде, с двумя приемными антеннами и коэффициентом 2 дискретизации с повышенной частотой, показаны на фиг.6. Улучшение вследствие разнесения очевидно. Кривые демонстрируют хорошее согласование между методом БПФ, отвечающим изобретению, и подходом прямого обращения матрицы.

Согласно другому упрощению вычислений, корректор откликов без искажений с минимальной дисперсией путем комбинирования с одинаковым усилением (ОБИМД-КОУ) может быть получен при условии пренебрежения пространственной корреляцией между разными каналами разнесения, т.е. путем задания недиагональных элементов матриц E0,.., EL равными нулю. В этом случае решение для w может быть получено путем решения множества из М несвязанных задач для каждого канала разнесения. Результат этой модели с двойной антенной системой показан на фиг.7. Улучшение, обеспечиваемое использованием второй антенны, очевидно.

Хотя изобретение описано в отношении ограниченного количества вариантов осуществления, специалистам в данной области очевидно, что в рамках сущности и объема нижеприведенной формулы изобретения могут быть реализованы другие варианты осуществления.

1. Способ приема сигнала, содержащий этапы, на которых

принимают сигнал расширенного спектра, содержащий целевой сигнал, и применяют процесс канальной коррекции к принятому сигналу для генерации скорректированного сигнала, причем этап применения процесса коррекции содержит этапы, на которых

оценивают канально-корреляционную матрицу R принятого сигнала,

преобразуют матрицу R в блочно-циркулянтную матрицу S,

выполняют преобразование Фурье (ПФ) над первым столбцом матрицы S и формируют диагональную матрицу Λ,

выполняют ПФ над вектором канального импульса и умножают его на матрицу, обратную матрице Λ, для генерации отводов фильтра частотной области, и

выполняют обратное ПФ над отводами фильтра частотной области для генерации весовых коэффициентов фильтра, применяемых к принятому сигналу для генерации скорректированного сигнала.

2. Способ по п.1, в котором ПФ является дискретным преобразованием Фурье (ДПФ).

3. Способ по п.1, в котором ПФ является быстрым преобразованием Фурье (БПФ).

4. Способ по п.1, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

5. Способ по п.2, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

6. Способ по п.3, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

7. Способ по п.1, в котором принятый сигнал выражают вектором из L_F элементов, и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

8. Способ по п.2, в котором принятый сигнал выражают вектором из L_F элементов и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

9. Способ по п.3, в котором принятый сигнал выражают вектором из L_F элементов и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

10. Способ по п.4, в котором принятый сигнал выражают вектором из L_F элементов и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

11. Способ по п.5, в котором принятый сигнал выражают вектором из L_F элементов и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

12. Способ по п.6, в котором принятый сигнал выражают вектором из L_F элементов и дополнительно содержащий этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

13. Способ приема сигнала в многоканальном устройстве, реагирующем на М каналов, содержащий этапы, на которых

принимают сигнал расширенного спектра, содержащий целевой сигнал, и применяют процесс канальной коррекции к принятому сигналу для генерации скорректированного сигнала,

осуществляют операцию кодовой корреляции на скорректированном сигнале для генерации выходного сигнала, представляющего целевой сигнал, и

обрабатывают выходной сигнал,

причем этап применения процесса коррекции содержит этапы, на которых

оценивают канально-корреляционную матрицу R принятого сигнала, причем матрица R имеет вид ленточной блочной матрицы Теплица, содержащей множество подматриц размера М×М,

преобразуют матрицу R в блочно-циркулянтную матрицу S, имеющую полиномиальное представление кронекеровых произведений,

выполняют поэлементное ПФ над первым блочным столбцом матрицы S и формируют блочно-диагональную матрицу F^-1,

выполняют ПФ по размерностям разнесения над вектором канального импульса и умножают на матрицу, обратную матрице F, для генерации отводов фильтра частотной области, и

выполняют обратное ПФ над отводами фильтра частотной области для генерации весовых коэффициентов фильтра, применяемых к принятому сигналу для генерации скорректированного сигнала.

14. Способ по п.13, в котором ПФ представляет собой ДПФ.

15. Способ по п.13, в котором ПФ представляет собой БПФ.

16. Способ по п.13, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

17. Способ по п.14, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

18. Способ по п.15, дополнительно содержащий этап, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

19. Способ по п.13, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

20. Способ по п.14, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

21. Способ по п.16, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

22. Способ по п.17, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

23. Способ по п.18, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (L_F/2) элементов.

24. Способ по п.19, в котором принятый сигнал выражают вектором из L_F элементов, и который дополнительно содержит этап, на котором осуществляют вычисления в частотной области с соответствующим вектором из 2L_F элементов, после чего преобразованный вектор во временной области усекают, удаляя первые и последние (Lp/2) элементов.

25. Система для приема сигнала, содержащая

средство для приема сигнала расширенного спектра, содержащего целевой сигнал,

средство для применения процесса канальной коррекции к принятому сигналу для генерации скорректированного сигнала,

средство для осуществления операции кодовой корреляции на скорректированном сигнале для генерации выходного сигнала, представляющего целевой сигнал, и

средство для обработки выходного сигнала, причем средство для применения процесса коррекции содержит средство для

оценивания канально-корреляционной матрицы R принятого сигнала,

преобразования матрицы R в блочно-циркулянтную матрицу S,

выполнения преобразования Фурье (ПФ) над первым столбцом S и формирования диагональной матрицы Λ,

выполнения ПФ над вектором канального импульса и умножения его на матрицу, обратную матрице Λ, для генерации отводов фильтра частотной области, и

выполнения обратного ПФ над отводами фильтра частотной области для генерации весовых коэффициентов фильтра, применяемых к принятому сигналу для генерации скорректированного сигнала.

26. Система по п.25, дополнительно включающая в себя средство для осуществления этапа, на котором прибавляют константу к диагональным элементам блочно-циркулянтной матрицы.

27. Система по п.26, в которой принятый сигнал выражается вектором из L_F элементов, и которая дополнительно включает в себя средство для осуществления вычисления в частотной области с соответствующим вектором из 2L_F элементов, с последующим усечением преобразованного вектора во временной области путем удаления первых и последних (L_F/2) элементов.

28. Система для приема сигнала в многоканальном устройстве, реагирующем на М каналов, содержащая

средство для приема сигнала расширенного спектра, содержащего целевой сигнал,

средство для применения процесса канальной коррекции к принятому сигналу для генерации скорректированного сигнала,

средство для осуществления операции кодовой корреляции на скорректированном сигнале для генерации выходного сигнала, представляющего целевой сигнал и

средство для обработки выходного сигнала,

причем средство для применения процесса коррекции содержит средство для оценивания канально-корреляционной матрицы R принятого сигнала, причем матрица R имеет вид ленточной блочной матрицы Теплица, содержащей множество подматриц размера М×М,

преобразования матрицы R в блочно-циркулянтную матрицу S, имеющую полиномиальное представление кронекеровых произведений,

выполнения поэлементного ПФ над первым блочным столбцом матрицы S и форми