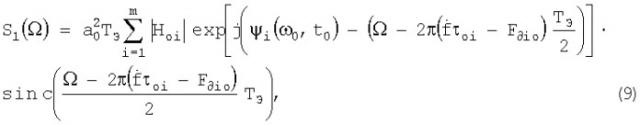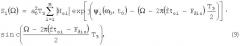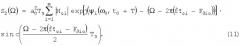Способ одновременного измерения частотных зависимостей доплеровского смещения частоты и времени распространения коротковолновых сигналов в ионосферной радиолинии

Способ одновременного измерения частотных зависимостей доплеровского смещения частоты и времени распространения коротковолновых сигналов в ионосферной радиолинии

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике и электросвязи и может быть использовано в системах частотного обеспечения коротковолновой (KB) радиосвязи для оперативного измерения основных параметров ионосферных линий связи и выбора оптимальных радиоканалов.

Надежность и качество голосовых и дискретных систем KB радиосвязи в первую очередь зависит от условий распространения сигналов в ионосферной радиолинии и помеховой обстановки. К наиболее важным особенностям ионосферной радиолинии, которые накладывают ограничения на использование высокоскоростных и широкополосных систем KB радиосвязи, относятся следующие ее основные свойства: многолучевость, обусловленная слоистой структурой ионосферы и магнитоионным расщеплением распространяющихся волн; частотные и временные вариации, обусловленные зависимостью показателя преломления ионосферы от частоты и времени. Влияние этих основных свойств ионосферной радиолинии на сигналы систем KB радиосвязи зависит от длины и географического расположения радиотрассы, диаграммы направленности передающей и приемной антенн, отношения центральной частоты излучаемого сигнала к максимально применимой частоте (МПЧ), которая, в свою очередь, зависит от времени суток, времени года, солнечной активности и протяженности радиотрассы. Параметры каждого приходящего луча испытывают быстрые флуктуации из-за движения неоднородностей, а также медленные флуктуации из-за изменения освещенности ионосферы. Наряду с этим вследствие движения слоев наблюдается доплеровский сдвиг частоты и вследствие движения неоднородностей - доплеровское уширение спектра сигнала. Дифференциальный доплеровский сдвиг между лучами на данной рабочей частоте приводит к интенсивным замираниям и значительным частотно-селективным помехам особенно высокоскоростным (широкополосным) системам связи. Даже относительно малые величины частотно-селективных и быстрых временных замираний распространения, приводят к неустраняемым (даже за счет повышения мощности сигнала) ошибкам.

В связи с этим для повышения эффективности современных систем KB радиосвязи необходимо постоянно знать условия распространения сигналов в ионосферной радиолинии между передающей и приемной станциями. Для этого организуют диагностику ионосферной радиолинии путем передачи «зондирующих» сигналов и их соответствующей обработки в приемнике, в результате которой определяют качество прохождения сигнала на каждой радиолинии и в каждом заданном радиоканале в конкретный момент времени. В настоящее время существует много способов диагностики ионосферной радиолинии, использующих в качестве зондирующих шумоподобные сигналы (ШПС или сложные) различной частотно-временной структуры. Применение таких сигналов позволяет существенно повысить помехозащищенность и разрешающую способность способов и систем диагностики. Из большого многообразия используемых для диагностики ионосферных радиолиний ШПС самое широкое распространение в настоящее время имеет непрерывный линейно частотно-модулированный (ЛЧМ) сигнал.

Известен способ одновременного определения зависимостей времени группового запаздывания и доплеровского смещения частоты от частоты излучения отдельных мод распространения KB с помощью периодических сигналов с линейной частотной модуляцией [Иванов В.А., Колчев А.А., Шумаев В.В. Влияние нестационарности однолучевого КВ-канала на характеристики сигналов с расширенным спектром. // Проблемы распространения и дифракции электромагнитных волн: М. МФТИ. 1994. С.73-79]. Недостатком этого способа является большое время измерения на одной частоте и, как следствие, большой частотный шаг между измерениями.

Способ одновременного определения доплеровского смещения частоты и времени группового запаздывания отдельных мод на основе трехэлементного ЛЧМ сигнала изложен в работе [Pool A.W.V. Advanced sounding The FMCW alternative // Radio Science /. - 1985. - V.20, №6. - P.1609-1616]. Использование фазовых измерений в этом способе позволяет уменьшить время измерения в одном частотном канале. Однако и в этом случае измерения производятся дискретно, в заранее заданных каналах при помощи трех сдвинутых во времени ЛЧМ сигналов с жестко заданными параметрами.

Предлагаемое изобретение устраняет эти недостатки, позволяя проводить одновременные измерения доплеровского смещения частоты и времени группового запаздывания отдельных мод в произвольных каналах декаметрового диапазона радиоволн путем использования двойного непрерывного ЛЧМ сигнала.

Способ состоит в следующем. Передатчик излучает одновременно два непрерывных ЛЧМ сигнала с одинаковыми параметрами: начальные частота и фаза, скорость изменения частоты. Различие состоит в начальном времени излучения: один сигнал смещен относительно другого на время Т (см. фиг.1а).

Если первый ЛЧМ сигнал а₁(t) имеет вид:

где f_H - начальная частота излучения;

- скорость изменения частоты;

a₀ - амплитуда излучаемого сигнала;

t - текущее время;

t₀ - время начала излучения;

t_K - длительность излучения,

то для второго сигнала в выражении (1) изменяется только время начала излучения:

Обработка принятого ЛЧМ сигнала в приемнике методом сжатия в частотной области состоит в умножении его на сигнал гетеродина, комплексно-сопряженный излучаемому сигналу, и в анализе спектра полученного сигнала разностной частоты. Для первого излученного сигнала этим операциям соответствуют следующие математические соотношения:

A₁(t)=a_1вых(t)·a₁*(t)

где A₁(t) - сигнал разностной частоты, соответствующий первому излученному сигналу;

S₁( Ω) - его спектр;

Ω - круговая частота;

a_1вых (t) - сигнал а₁(t) на выходе из ионосферной радиолинии (на входе приемника);

а₁*(t) - сигнал, комплексно-сопряженный сигналу а₁(t).

Для определения времени группового запаздывания отдельных мод распространения KB сигнал разностной частоты разбивается на N элементов длительностью T_Э с шагом между элементами ΔT_Э и для каждого элемента вычисляется преобразование Фурье [Иванов В.А., Рябова Н.В., Шумаев В.В. Основы радиотехнических систем ДКМ диапазона: Учебное пособие. - Йошкар-Ола: МарГТУ, 1998, - с.155-159]. В излучаемом сигнале каждому элементу будет соответствовать ЛЧМ сигнал с полосой и базой B_Э=Δf_Э·T_Э. Если Гц/с и Т_Э=1 с, то В_Э=10⁵, а Δf_Э=100 кГц. Поскольку Δf_Э<<f (f - текущая частота), то каждый элемент разностного сигнала относят к центральной частоте элемента Δf_Э. Соответственно спектр элемента сигнала также можно отнести к этой частоте.

Чтобы найти спектр первого элемента разностного сигнала, используем подход, основанный на представлении среды распространения передаточной функцией H(ω, t), которую в случае многолучевого нестационарного канала распространения можно представить в виде:

где |Н_i(ω, t)| - модуль передаточной функции отдельного луча;

ω=2πf;

ϕ_i(ω, t) - набег фазы отдельного луча в ионосферной радиолинии;

m - число мод распространения.

Элемент зондирующего сигнала занимает некоторую полосу около частоты f₀. Считая канал, квазистационарным для небольших масштабов времени Δt=t-t₀, фазу передаточной функции отдельного луча, при отсутствии частотной дисперсии, можно разложить в ряд Тейлора по степеням Δω=2π·(f-f_H) и Δt, ограничившись линейными слагаемыми, а |Н_i(ω, t)|· считать постоянным:

ϕ_i(ω, t)≈ϕ_i(ω₀, t₀)+ϕ′_it(ω₀, t₀)Δt+ϕ′_iω(ω₀, t₀)Δω,

где и - соответствующие производные,

|H_oi| - постоянное значение модуля передаточной функции отдельного луча.

Известен физический смысл коэффициентов разложения фазы (5). Так первая производная по частоте для i-й моды равна времени группового запаздывания сигнала этой моды τ_i:

Зависимость фазы сигнала i-й моды от времени связана с доплеровским смещением частоты этой моды F_∂i:

Квазистационарность канала и отсутствие частотной дисперсии предполагают, что в полосе частот элемента сигнала за время его длительности τ_i(ω; t) и F_∂i(ω; t) не изменяются, т.е. τ_i(ω; t)=τ_i(ω₀; t₀)=τ_oi=const и F_∂i(ω; t)=F_∂i(ω₀; t₀)=F_∂io=const, где τ_oi и F_∂io - постоянные значения времени запаздывания и доплеровского смещения частоты i-го луча.

При обработке методом сжатия в частотной области длительность элемента сигнала Т_Э при спектральном анализе много больше времени запаздывания сигнала в ионосферном радиоканале: Т_Э>>τ_oi. Тогда А₁(t), с учетом (3), можно записать в виде:

где - начальная фаза сигнала разностной частоты; a - его частота.

Как видно из (8) отдельный элемент разностного сигнала на протяжении Т_Э представляет собой отрезок гармонического колебания. С учетом этого S₁( Ω) можно записать в виде:

где sinc(x), как функция переменной х, определяется соотношением .

Если для второго излученного сигнала записать аналогичные соотношениям (3) преобразования:

A₂(t)=a_2вых(t)·a₂*(t)

где A₂(t) - сигнал разностной частоты, соответствующий второму излученному сигналу; S₂( Ω) - его спектр; a_2вых(t) - сигнал a₂(t) на выходе из ионосферы, то для спектра первого элемента его разностного сигнала получим:

Сравнивая (9) и (11), видим, что в этих выражениях амплитуды совпадают, а различаются только фазы _i.

Модули |S₁( Ω)| и |S₂( Ω)| имеют максимумы на частотах . Для условий ионосферного распространения , поэтому

.

Если в результате многолучевости в точку приема одновременно приходит несколько лучей с разной задержкой τ_oi, то каждому из них будет соответствовать своя разностная частота (см. фиг.1б и фиг.2а, где F_i - разностная частота различных мод распространения). При этом разрешающая способность по частоте δF при спектральной обработке сигнала длительностью Т_Э задается соотношением

.

Отсюда разрешающая способность по задержке δτ будет равна:

Если Δψ_i - разность фаз между спектральными составляющими Ω_oi для S₂( Ω) и S₁( Ω), то, с учетом (4) и (7), имеем:

Из (13) следует, что

.

Смещение Т необходимо выбирать таким образом, чтобы |Δψ_I|=|2πF_∂ioT|∈(0; π). Тогда

.

При ионосферном распространении KB обычно выполняется условие F_∂io<10 Гц. Следовательно, Т<0,05 с.

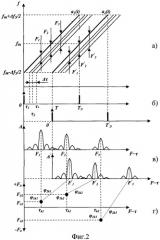
Рассмотрим предлагаемый способ по диаграммам фиг.2, на которой представлены основные процедуры и этапы обработки принимаемого сигнала и измерения доплеровского смещения частоты и времени распространения элемента двойного ЛЧМ сигнала на выходе диагностируемой ионосферной радиолинии. На фиг.2а толстыми линиями изображен один элемент двойного непрерывного ЛЧМ сигнала с длительностью Т_Э, диапазоном частот Δf_Э и центральной частотой f_0K, а тонкими линиями изображен многолучевой сигнал на выходе ионосферной радиолинии, состоящий из трех сигналов с различными временами распространения τ₁÷τ₃ и доплеровскими смещениями частоты F_∂1÷F_∂3. Здесь же показаны частоты F₁÷F₃ «сжатых» в частотной области трех разностных сигналов, получаемых в результате перемножения принимаемого сигнала с сигналом гетеродина приемника, комплексно сопряженному излучаемому сигналу и выделения низкочастотной составляющей. Проводя одинаковое разбиение как двойного непрерывного ЛЧМ сигнала (см. фиг.1а), так и каждого разностного сигнала, как показано на фиг.2б (здесь Т - время задержки второго ЛЧМ сигнала относительно первого), и выполняя преобразования Фурье для каждого элемента, получаем две последовательности спектральных отсчетов. Эти отсчеты являются комплексными числами, что дает возможность определить амплитуду и фазу спектральных составляющих каждого элемента разностного сигнала.

Для определения времени группового запаздывания используется амплитудный спектр разностного сигнала. Частоты Ω_oki, на которых наблюдаются максимумы модуля спектра k-го элемента сигнала разностной частоты, соответствуют задержкам различных мод распространения

на частоте

.

На фиг.2в показаны спектры сжатых в частотной области каждого из элементов ЛЧМ сигнала с центральной частотой f_0k на выходе ионосферной радиолинии. Для элемента первого ЛЧМ сигнала согласно (9) в случае трех принимаемых сигналов (мод) имеем три спектральные составляющие вида с амплитудами |Н_0i|, частотами F_i=2π Ω_0i и фазами ϕ_i(ω₀, t₀). Для элемента второго ЛЧМ сигнала согласно (11) имеем также три спектральные составляющие вида с такими же амплитудами и частотами, но с другими фазами ϕ_i(ω₀, t₀+T). Если ϕ_1ik и ϕ_2ik - фазы спектральной составляющей Ω_oki. Для k-го элемента первого разностного сигнала и разностного сигнала, смещенного на время Т, соответственно (k=1, 2... N), то доплеровское смещение частоты для элемента сигнала каждой (i) моды распространения с центральной частотой

находится по формуле:

На фиг.2г для элемента двойного ЛЧМ сигнала с центральной частотой f_0k в координатной системе доплеровского смещения частоты и времени распространения сигнала показана процедура отображения (регистрации) результатов совместной обработки спектров разностных сигналов. Время распространения сигнала (группового запаздывания) различных мод пропорционально частотам максимума модуля спектра разностного сигнала , а доплеровское смещение частоты различных мод распространения сигнала пропорционально разности фаз соответствующих спектральных составляющих первого и второго (смещенного на время Т) разностного сигналов согласно формуле (14).

Регистрируя изменения в положении максимумов модуля спектра сигнала разностной частоты (см. фиг.2в) от элемента к элементу при изменении рабочей частоты от f_H до f_K, получаем частотную зависимость времени группового запаздывания τ_ki(f_0k) (ионограмма) для диагностируемой ионосферной радиолинии (см. фиг.1б). Ионограмма представляет собой трехмерное изображение данных ЛЧМ диагностики. По горизонтали откладывается частота в диапазоне от 2 до 30 МГц, по вертикали - время распространения τ (время группового запаздывания). Третье измерение - мощность сигнала для каждого частотного элемента в дБ относительно заданного уровня.

Вычисляя по формуле (14) значение F_∂ik для каждого элемента сигнала, получаем частотную зависимость доплеровского смещения частоты F_∂ik = F_∂i(f_0k) (доплерограмма) для диагностируемой ионосферной радиолинии (см. фиг.1в). Доплерограмма представляет собой трехмерное изображение результатов вычисления предлагаемым способом. По горизонтали откладывается частота в диапазоне от 2 до 30 МГц, по вертикали - доплеровское смещение частоты для каждой моды распространения. Третьим измерением также выступает мощность сигнала.

Следовательно, в диапазоне частот от f_H до f_K для каждой принимаемой моды сигнала определяются последовательности F_∂i(f_0k) и τ_i(f_0k). Важным преимуществом предлагаемого способа одновременного измерения доплеровского смещения частоты и времени распространения сигнала в ионосферной радиолинии с применением двойного непрерывного ЛЧМ сигнала состоит в том, что параметры разбиения разностного сигнала T_Э, ΔT_Э(Δf_Э) являются параметрами обработки принятого непрерывного ЛЧМ сигнала и могут быть выбраны произвольным образом, не изменяя исходной структуры излучаемого сигнала, что позволяет определить F_∂i и τ_i, для любой интересующей нас рабочей частоты f_p.

Таким образом, применение предлагаемого способа в системах диагностики ионосферных радиолиний непрерывным ЛЧМ сигналом в отличие от известного позволит оперативно получать частотные зависимости доплеровского смещения частоты и времени распространения сигнала в ионосферной радиолинии во всем ДКМ диапазоне радиоволн, на основании которых обеспечиваются устойчивые высокоскоростные и гибкие каналы передачи информации для существующих систем KB радиосвязи.

Способ одновременного измерения частотных зависимостей доплеровского смещения частоты и времени распространения коротковолновых сигналов в ионосферной радиолинии для отдельных мод распространения, заключающийся в излучении передатчиком непрерывного линейно-частотно-модулированного (ЛЧМ) сигнала с начальной частотой излучения f_H и скоростью изменения f и обработки его в приемнике методом сжатия в частотной области, отличающийся тем, что на передаче добавляется второй непрерывный ЛЧМ сигнал с идентичными первому параметрами и смещенный относительно него на время Т, а на приеме путем разбиения сигналов разностной частоты на элементы длительностью Т_Э с шагом между элементами ΔТ_Э и определения частот Ω_oki и фаз ϕ_1ki и ϕ_2ki спектральных составляющих выбранной i-й моды, на которых наблюдаются максимумы модуля спектра k-го элемента первого разностного сигнала и разностного сигнала смещенного на время Т, измеряют времена группового запаздывания τ_ki и доплеровское смещение частоты F_∂ik различных мод распространения на частотах f_H + fΔT_Э(k - 1/2) по формулам:

и

где k - номер элемента сигнала.