Нейронная сеть для преобразования остаточного кода в двоичный позиционный код

Нейронная сеть для преобразования остаточного кода в двоичный позиционный код

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах для реализации операции вывода данных.

Известно устройство для преобразования числа из системы остаточных классов в позиционный код (а.с. 1005028, G06F 5/02), содержащее сдвиговый регистр, блок синхронизации, блок памяти констант и позиционный накапливающий сумматор. Однако такое устройство характеризуется высокой сложностью.

Наиболее близким по технической сущности к заявленному устройству является преобразователь кодов из системы остаточных классов в двоичный позиционный код (а.с. 813408, G06F 5/02), содержащий входной регистр, дешифраторы, преобразователь кодов из системы остаточных классов в полиадический код, группу элементов ИЛИ, элементы задержки и сумматор. Недостатком этого устройства является сложность группы элементов ИЛИ при использовании больших модулей системы остаточных классов и сложность преобразователя остаточного кода в полиадический, который реализует последовательный алгоритм Гарнера.

Целью настоящего изобретения является сокращение оборудования преобразователя остаточного кода в двоичный позиционный код. Поставленная цель достигается тем, что в преобразователь введены нейронные сети конечного кольца и постоянные запоминающие устройства. Таким образом, нейронная сеть для преобразования остаточного кода в двоичный позиционный код будет состоять из входного слоя нейронных сетей, выполняющих роль регистров, параллельного преобразователя остаточного кода в полиадический код, постоянных запоминающих устройств и параллельного взвешенного сумматора.

Обратное преобразование числа из модулярного представления в двоичную форму базируется на классической теореме из теории чисел, которая называется Китайской теоремой об остатках (КТО). На основании известного представления чисел в СОК (α₁, α₂, ..., α_n) КТО делает возможным определение числа в ПСС , если наибольший общий делитель любой пары модулей равен 1.

КТО имеет вид

где , для (p_i,p_j)=1 для i≠j

α_i - остаток числа x по модулю p_i, для i=1, 2, ..., n.

Используются разные формы китайской теоремы об остатках (КТО). Из (1) видно, что из КТО получаем , а не само X. Если известно, что x находится между 0 и P-1, то можно записать

В некоторых случаях желательно иметь вид КТО, где сумма появляется без оператора по модулю Р. Это можно сделать путем определения вспомогательной функции R(x), так чтобы

где .

R(x) - это функция x, определяемая для любого целого числа x.

Из КТО видно, что выражение

отличается от x кратным значением P, эта разность равна - P·R(x).

Функция R(x) называется рангом числа и широко используется при вычислениях в модулярной арифметике.

Ранг числа R(x) показывает сколько раз нужно вычесть величину диапазона P из полученного числа, чтобы вернуть его в диапазон. Таким образом, если найдены P_i, и ранг числа R(x), то для перевода числа достаточно вычислить и ввести эту сумму в диапазон [0,P] вычитанием величины, кратной P. Недостаток рассмотренного метода заключается в том, что приходится иметь дело с большими числами P_i и, кроме того, действия сложения и умножения надо выполнять в позиционной системе счисления, а полученный результат необходимо вводить в диапазон вычитаемой величины, кратной P.

Необходимо отметить, что P_i и являются константами выбранной системы и определяются заранее, а ранг числа R(x) - переменная величина и сложность ее вычисления линейно зависит от числа оснований СОК, что приводит к еще более сложной процедуре восстановления числа.

Кроме того, применение КТО для восстановления числа требует сложных вычислений в модулярном нейрокомпьютере, так как элементарные процессоры выполняют операции по модулю p_i, где i=1, 2, ..., n, а не по модулю P=p₁p₂...p_n, как это требуется по КТО.

Из выражения (2) видно, что для его отображения необходимы сумматоры по модулю P. Эту нежелательную особенность можно обойти при помощи отображения СОК на ассоциированное представление со смешанным основанием, а затем и на двоичное представление. Коэффициенты a_i могут быть представлены с помощью n цифр со смешанными основаниями. Отображение из СОК в обобщенную позиционную систему счисления (ОПСС) может быть определено рекурсивно с помощью операций по малым модулям p_i.

Для перехода от вычислений по модулю P к вычислению по модулям p_i предлагается метод восстановления чисел на основе совместного использования КТО и ОПСС.

Пусть задана система оснований p₁, p₂, ...p_n, с диапазоном P=p₁p₂...p_n, и ортогональными базисами B₁, B₂, ..., B_n, которые определяются как

где m_i - веса ортогональных базисов.

Тогда КТО можно представить в виде

где α_i - остатки (вычеты) числа X по mod p_i;

R(x) - ранг числа.

Представим ортогональные базисы B_i в ОПСС, тогда

где b_ij - коэффициенты ОПСС, i,j=1, 2,..., n.

На основании (7) запишем X_ОПСС, выражение (6) в виде

Так как B_i mod p_i=0, ∀j>i, то перед первым значащим разрядом будет i-1 нулей.

Для удобства вычислений базисы можно представить в виде матрицы

Тогда X_ОПСС, запишется как

При этом

где: a_i - коэффициенты ОПСС числа x;

α_i - вычеты числа x по mod p_i;

b_ij - ортогональные базисы, представленные в ОПСС; i,j=1, 2, ..., n.

При использовании традиционной вычислительной базы произведения α_ib_ij mod р_i можно поместить в память, а адресами будут являться остатки α_i.

Если вычислительная база представлена в нейросетевом базисе, тогда в качестве весовых коэффициентов нейронной сети будут выступать b_ij, а в качестве входных сигналов - остатки α_i.

Последовательность вычислений для первого варианта имеет вид

Для определения всех цифр ОПСС требуется две операции: одна операция для выборки из памяти и одна операция для суммирования. По сравнению с известным последовательным методом Гарнера выигрыш определяется выражением . Для реализации этого метода в нейропроцессоре необходимо иметь средства для выполнения модулярных операций, например нейронные сети конечного кольца по p_i основаниям, где i=1, 2, ..., n.

Пример. Пусть основания системы p₁=3, p₂=5, p₃=7, p₄=2. Дано число x=(2,3,0,1), представленное в СОК по выбранным модулям. Найти представление этого числа в ОПСС, то есть x=[a₁,a₂,a₃,a₄]. На основании выражения (5) определим ортогональные базисы СОК: B₁=70, B₂=126, B₃=120, B₄=105. Представим базисы B_i в ОПСС, тогда b_ij:

.

В связи с тем, что константы b_ij определяются выбором системы модулей СОК, то их с учетом переноса в i-разрядах можно поместить в память, тогда процесс преобразования можно представить в виде

Для определения всех цифр ОПСС требуется две операции: одна операция для выборки из памяти и одна операция для суммирования. По сравнению с последовательным итерационным процессом выигрыш равен n-1, где n - число модулей СОК.

Полученные значения коэффициентов ОПСС числа x используем для образования двоичного кода.

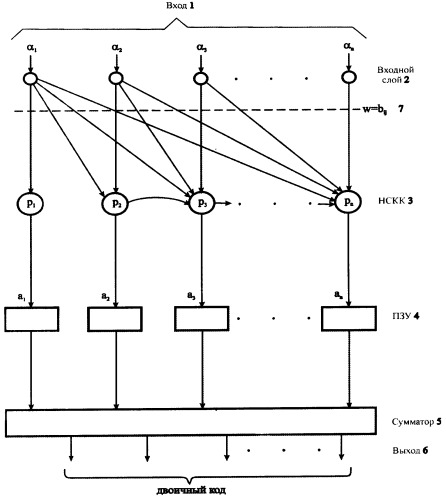
Нейронная сеть для преобразования остаточного кода в двоичный позиционный код представлена на чертеже.

Нейронная сеть содержит входной слой нейронов 2, n-нейронных сетей конечного кольца (НСКК) 3, n-постоянных запоминающих устройств (ПЗУ) 4, сумматор 5, вход нейронной сети 1, выход нейронной сети 6 и весовые коэффициенты и w=b_ij 7.

Входной слой 2 предназначен для временного хранения входного остаточного кода, то есть он выполняет роль регистра.

НСКК преобразует остаточный код в код ОПСС, при этом число представляется в виде, соответствующем ОПСС, следующим образом X=a₁+a₂p₁+a₃p₁p₂+...+a_np₁p₂...p_n-1, где a_i - называется коэффициентом ОПСС, причем 0≤a_i<p_i. Весовой коэффициент, связанный с каждой цифрой ОПСС a_i, равен p₁p₂...p_i-1. Такая система имеет тот же диапазон представления, что и система остаточных классов p=p₁p₂...p_n. Коэффициенты кода ОПСС являются адресами памяти, где хранятся значения произведений a_ip₁p₂...p_i-1. Двоичные эквиваленты значений a_ip₁p₂...p_i-1, хранящиеся в памяти, поступают на вход сумматора, где по остаткам восстанавливается двоичное число.

Нейронная сеть для преобразования остаточного кода в двоичный позиционный код работает следующим образом.

Входное число x=(α₁, α₂, ..., α_n), представленное в системе остаточных классов своими остатками α_i по модулям p_i (i=1, 2,..., n), поступает на входной слой 2. Входной слой связан с n НСКК. При выбранных модулях СОК структура нейронной сети зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов w=b_ij 7, определенных выражением (7) НСКК p₁, p₂, ..., p_n 3 реализуют вычислительную модель (10), на выходах которой формируются коэффициенты ОПСС a_i () числа x. Коэффициенты a_i являются входными адресами ПЗУ_i 4, где хранятся двоичные эквиваленты a_ip₁p₂...p_i-1. Считанные из ПЗУ_i двоичные коды, соответствующие произведению a_ip₁p₂...p_i-1, суммируются взвешенным сумматором 5. На выходе 6 формируется двоичный код. Время преобразования кода определяется n-тактами синхронизации. Структура преобразователя, реализованная на СБИС, требует n-НСКК по модулям p_i, n-ПЗУ_i, каждое из которых хранит p_i слов разрядностью, эквивалентной числу (p_i-1)p₁p₂...p_i-1 и одного параллельного сумматора с ускоренным переносом. Сумматор может быть реализован по типу дерева, тогда время преобразования определяется выражением [log n], где n - число модулей СОК.

Нейронная сеть для преобразования остаточного кода в двоичный позиционный код, содержащая входной слой нейронов, n-нейронных сетей конечного кольца и сумматор, отличающаяся тем, что в нее введены n-постоянных запоминающих устройств для хранения двоичных эквивалентов значений a_ip₁p₂...p_i-1 (i=1, 2, ..., n), адресными входами которых являются выходы n-нейронных сетей конечного кольца, реализующие вычислительную модель ,

где α_i - разряды системы остаточных классов (СОК), a - коэффициенты обобщенной позиционной системы счисления (ОПСС); b_ij - ортогональные базисы, представленные в ОПСС; i, j=1, 2, ..., n, p_i - модуль СОК, входами которых являются выходы нейронов входного слоя, а выходами нейронной сети являются выходы сумматора, входами которого являются выходы n-постоянных запоминающих устройств, по которым поступают двоичные эквиваленты значений a_ip₁p₂...p_i-1.