Способ управления скоростью летательного аппарата

Способ управления скоростью летательного аппарата

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области авиастроения. Может быть использовано в космической и ракетной технике, судостроении и других областях при решении задач управления динамическими объектами.

Для управления скоростью летательного аппарата (ЛА) могут быть использованы различные математические методы управления и соответствующие им способы отыскания необходимого управления. Широко известны способы управления скоростью ЛА, базирующиеся на таких методах, как [1];

- метод передаточных функций;

- метод вариационного исчисления;

- принцип максимума Понтрягина;

- методы оптимизации по классическим и неклассическим функционалам (АКОР).

Известен способ управления динамическими объектами, в том числе их скоростью, основанный на идее использования эталонных моделей [2, 3]. Существо данного способа управления заключается в следующем [3 с.44]. С помощью системы дифференциальных уравнений задают желаемый характер изменения координат вектора состояния. С помощью датчиков измеряют текущий вектор состояния. Далее определяют вектор «невязки» (рассогласование) как разность между координатами эталонной модели и текущими координатами ЛА. На основе вектора невязки формируют сигналы управления по линейному закону. Рулевые поверхности ЛА отклоняют на величины, пропорциональные сигналам управления. За счет их отклонения обеспечивают наилучшее приближение реальной траектории к эталонной. Данный способ управления наиболее близок к предлагаемому, поэтому примем его за прототип.

Указанный способ управления имеет ряд положительных свойств, в частности низкую чувствительность к изменению структуры параметров как математических моделей, по которым выполняют синтез алгоритмов и вычисление сигналов управления [3 с.55].

Недостатками способа управления являются следующие особенности. Во-первых, алгоритмы управления синтезированы без учета скорости ветра, который на высотах 8-10 км может достигать значений до 100 км/ч (горизонтальная составляющая), что при вертикальных маневрах, особенно при приводит к заметным ошибкам при отслеживании заданной траектории. Здесь и далее Н - высота полета. Во-вторых, эталонные модели строят таким образом, что они ориентированы лишь на один канал управления, имеющий одно управление, в то время как на объекте управления (ЛА) каналы взаимосвязаны по отклонению рулей (Приложение 1, формула (12)). Это также приводит к ошибкам управления при слежении за заданным эталонным движением.

Задачей предлагаемого изобретения является повышение точности управления ЛА относительно заданной траектории движения путем изменения способа управления вектором скорости движения ЛА.

Сущность предлагаемого изобретения заключается в обеспечении инвариантности по отношению к скорости ветра и компенсации взаимосвязей между каналами управления путем усовершенствования закона управления.

Рассмотрим условия решения поставленных задач. В связанной системе координат (х, у, z) уравнение сил имеет следующий вид [4 с.30]:

где V_kx, V_ky, V_kz - проекции вектора земной скорости ЛА в связанной системе координат (ССК); ω_x, ω_y, ω_z - проекции вектора угловой скорости ССК;

- главный вектор сил в проекциях на оси ССК; m=m(t)-масса ЛА.

Далее будем полагать, что известен вектор - вектор заданных проекций земной скорости на оси ССК. Вектор вычисляют при постоянном векторе тяги . Здесь - сила тяжести; - вектор суммарной аэродинамической силы. Вычисление данных составляющих более подробно приведено в Приложении 1, (формулы (5), (11), (12)).

В данных формулах учтены отклонения тормозных щитков (δ_тщ), предкрылков (δ_пр), которые используют на взлетно-посадочных режимах.

Предлагаемый способ позволяет учесть и другие устройства механизации крыла ЛА.

Полагаем, что заданы характеристики переходного процесса, которые представлены в форме «эталонной модели» [3]. Ее вид представлен в Приложении 1 (формула 3). На первом этапе вычисляют сигналы управления, пропорциональные величине аэродинамической силы, записанной в форме перегрузок (формула (5) Приложение 1). Для поиска величины управления используют градиентный метод на основе минимизации квадратичного функционала. Вид функционала определен формулой (4) Приложения 1.

Сущность известного способа (прототипа) состоит в применении указанного первого этапа формирования управления. В предлагаемом изобретении предлагается использовать второй этап. Отличительными признаками его являются следующие операции. Во-первых, для обеспечения инвариантности по отношению к ветровым возмущениям необходимо учитывать значение ветра в форме вектора скорости в законе управления. Для этого необходимо вычислять вектор воздушной скорости с учетом вектора скорости ветра (формула (11) Приложения 1). Во-вторых, на основе вычисленных сигналов управления определяют необходимое положение органов управления с учетом взаимного влияния каналов управления и наличия органов механизации крыла. Алгоритм вычисления необходимого положения рулей приведен в Приложении 1 (формула (12)). На основе алгебраических соотношений возможно вычисление положения нулей при учете взаимосвязей между каналами управления.

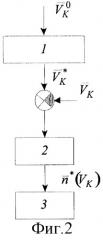
Блок-схема существующего способа представлена на фиг.2. Здесь цифрой 1 обозначена эталонная модель. Выход ее соединен со входом блока 2, представляющего собой усилительное звено через сумматор. Сигнал , пропорциональный величине отклонения нулей, подают на объект управления 3, которым является ЛА.

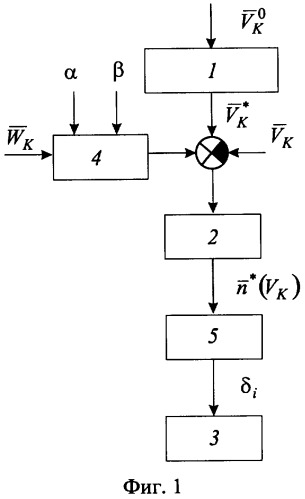
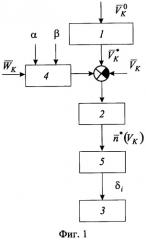
Блок-схема предлагаемого способа управления представлена на фиг.1. Здесь дополнительно используют операцию пересчета скорости ветра в связанную систему координат через углы атаки (α) и скольжения (β) (блок 4). Пересчет выполняют по формуле (11) Приложения 1. Далее по формулам (12) Приложения 1 выполняют расчет требуемого положения рулей δ_н, δ_э, δ_в (блок 5).

1. Справочник по теории автоматического управления./ Под редакцией А.А.Красовского. М.: Наука, 1997.

2. Подчукаев В.А. Теория автоматического управления. (Аналитические методы): Учебн. для вузов. - М.: физ. - мат. лит., 2005.

3. Крутько П.Д. Обратные задачи динамики в теории автоматического управления. Цикл лекций: Учебн. пособие для вузов. - М.: Машиностроение, 2004.

4. Буков В.Н. Адаптивные прогнозируемые системы управления полетом. - М.: Наука, Гл. ред. физ. - мат. лит., 1987.

Приложение 1

Синтез алгоритмов управления скоростью летательного аппарата

Пусть объект управления описывается уравнениями линейных скоростей для траекторного контура

где вектор V_K - вектор земной скорости летательного аппарата (ЛА) в связанной системе координат, Ω - кососимметрическая матрица угловых скоростей специального вида, n - вектор перегрузок, ε₂ - второй столбец матрицы направляющих косинусов [1].

Обозначим «новый» вектор входных воздействий .

Тогда уравнение 1 принимает вид

или в развернутой форме запишется как

В последней формуле введем обозначения:

Формулировка задачи управления. Пусть в каждый момент времени t состояние объекта (1) характеризуется значениями линейных скоростей V_kS(0). Требуется найти такие управляющие воздействия δ_i (i=1, 2, 3), при которых объект (1) переходит из состояния V_kS(0) в новое состояние и находится в этом состоянии бесконечно долго. Если , то линейные скорости определяют требуемый профиль полета (пространственную траекторию движения ЛА). При этом необходимо, чтобы линейные скорости управляемого движения по каждой степени свободы с требуемой точностью следовали за скоростями, определяемыми эталонными моделями

где χ_S1, χ_S0 - заданные коэффициенты; при t→∞; S=1, 2, 3.

Степень приближения управляемого процесса определяется функционалом

который характеризует энергию ускорения поступательного движения в окрестности фазовых траекторий эталонных моделей.

Если в качестве управляющих функций выбирать не отклонения рулей δ_i ЛА, а управляющие силы F_S и эквивалентные им перегрузки n* и то задача управления может быть решена поэтапно. Здесь G=mg.

На первом этапе синтезируют управляющие воздействия , а затем из силовых характеристик ЛА и формул: [3]

где - матрица направляющих косинусов между связанной и скоростной системами координат,

определяют законы управления рулями .

Здесь - заданные значения перегрузок, P=const - тяга двигателей.

Законы управления n*(V_k) по каждой степени свободы получаем, используя метод простого градиента

Согласно (2), (4) компоненты градиента (7) равны

Отсюда следует, что

или после интегрирования обеих частей данного уравнения получим

где требуемые значения вычисляют из (3).

Структура матрицы определяется характером перекрестных связей в уравнениях (6)

Управляющие воздействия определяют из уравнений (5), (6). С одной стороны, из уравнений (5) вычисляем коэффициенты аэродинамических сил

где

где ΔW_i, i=1, 2, 3 - проекции вектора скорости ветра. С другой стороны, выписываются уравнения (6), в которых неизвестными являются рули Следовательно, через вычисленные значения коэффициентов аэродинамических сил можно получить следующую систему алгебраических уравнений

или после преобразования

Синтезированные законы управления (12) формируют как функции, зависящие от перегрузок, то есть δ_в=δ_в(n_y), δ_э=δ_э(n_x, n_y), δ_н=δ_н(n_x, n_y, n_z) или, другими словами, как зависимости от управляющих сил F_i(i=x, y, z).

В эталонных моделях (3) каналы считаются независимыми. Для компенсации взаимного влияния каналов (формула(2)) в матрице коэффициентов усиления R кроме диагональных элементов предусмотрены дополнительные члены, позволяющие осуществить развязку каналов.

Литература к приложению 1

1. Корн Г., Корн Т. Справочник для научных работников и инженеров. - М.: Наука, 1984.

2. Машиностроение. Энциклопедия. T.1-4. Автоматическое управление. Теория. - М.: Машиностроение, 2000.

3. Красовский А.А. Основы теории авиационных тренажеров. - М.: Наука, 1995.

Способ управления скоростью летательного аппарата, заключающийся в формировании характеристик переходного процесса с помощью эталонной модели, вычислении разности эталонного и текущего векторов скоростей, на основе которой формируют сигналы управления с помощью линейного регулятора, отличающийся тем, что для повышения точности управления учитывают скорость ветра, для чего ее пересчитывают из земной системы координат в связанную через матрицу направляющих косинусов аэродинамических углов, а также вычисляют положение рулевых поверхностей из системы алгебраических уравнений, определяющих взаимосвязи между аэродинамическими силами и отклонениями рулевых поверхностей.