Способ запуска двухступенчатой управляемой ракеты с воздушного носителя

Способ запуска двухступенчатой управляемой ракеты с воздушного носителя

Иллюстрации

Показать все

Реферат

Изобретение относится к области техники вооружения, в частности к области управляемых ракет противотанковых ракетных комплексов (ПТРК) воздушного базирования.

При запуске с воздушного носителя управляемых ракет с отделяющимися элементами конструкции должны быть предприняты меры, исключающие столкновение отделившихся элементов конструкции ракеты с носителем.

Известен способ запуска противотанковой управляемой ракеты (ПТУР) Hellfire с помощью маршевого твердотопливного ракетного двигателя, который работает в течение 3 с, разгоняя ракету до скорости 500 м/с [Сборник научно-технической информации, Спецвыпуск. - Тула: ГУПКБП, 2005, с.5-26].

Известен также способ запуска ПТУР Spike с помощью двигательной установки, состоящей из двух двигателей: стартового (неотделяемого) двигателя и разгонно-маршевого двигателя. Стартовый двигатель (СД) обеспечивает выход ракеты из транспортно-пускового контейнера (ТПК) со скоростью 25 м/с. Затем включается маршевый двигатель, разгоняет ракету до скорости 180 м/с, после чего тяга двигателя снижается до величины, достаточной для сохранения скорости полета [Сборник научно-технической информации, №3(13) - Тула: ГУПКБП, 2005, с.24-58, с.62-76].

При этих способах запуска ракета не имеет отделяющихся элементов конструкции и не требуется применение специальных мер, призванных обезопасить носитель от отделяющихся частей ракеты.

Наиболее близким к предлагаемому является способ запуска управляемой ракеты Mistral 1/2 (АТАМ), двигательная установка которой состоит из отделяющегося СД и маршевого двигателя. Ракета, находящаяся в ТПК, установленном на пусковой установке воздушного носителя, запускается с помощью СД, который за время движения ракеты по ТПК сообщает ей начальную скорость 40 м/с и через 0,4 с после выхода из контейнера отделяется от ракеты, неуправляемой на стартовом участке траектории полета, и падает вниз. После чего включается маршевый двигатель и разгоняет ракету до скорости 850 м/с. [Jane's Air-Launched Weapons, 2005 March, ISSUE 45, р.13-14].

Стартовый двигатель, отделившийся от ракеты Mistral 1/2 (АТАМ), летящей с дозвуковой скоростью, представляет собой неоперенное тело вращения малого удлинения (λ<2) с большим коэффициентом сопротивления и практически нулевой подъемной силой. Под действием силы тяжести отделившийся СД падает вниз, и его траектория движения проходит ниже носителя, который продолжает сохранять направление полета, предшествующее пуску ракеты, или выполняет вертикальный маневр. Следовательно, и в этом наиболее близком к предлагаемому способу запуска ракеты с воздушного носителя нет необходимости предусматривать специальные меры, исключающие столкновение носителя с отделившейся стартовой ступенью.

Задачей предлагаемого изобретения является создание безопасного способа запуска с воздушного носителя противотанковой двухступенчатой управляемой ракеты с дальностью поражения цели более 20 км, управление которой осуществляется сразу после ее выхода из ТПК, а стартовый двигатель отделяется после того, как разгоняет ракету до максимальной скорости.

Для решения указанной задачи в предлагаемом способе запуска двухступенчатой управляемой ракеты с воздушного носителя, включающем пуск ракеты с помощью стартового двигателя из транспортно-пускового контейнера (ТПК), размещенного на пусковой установке, разделение ступеней ракеты после окончания работы стартового двигателя, баллистический полет стартовой ступени и управляемый полет маршевой ступени, управление ракетой осуществляют с момента ее выхода из ТПК, отделение стартовой ступени, выполненной в виде аэродинамически устойчивого оперенного тела вращения, производят после достижения ракетой максимальной скорости полета, а ТПК перед пуском ракеты поворачивают на угол, заранее рассчитанный для конкретных режимов полета носителя по данным о характере управления ракетой и известным аэродинамическим характеристикам ракеты и стартовой ступени, при котором вся совокупность возможных траекторий отделившейся стартовой ступени проходит ниже высоты полета носителя.

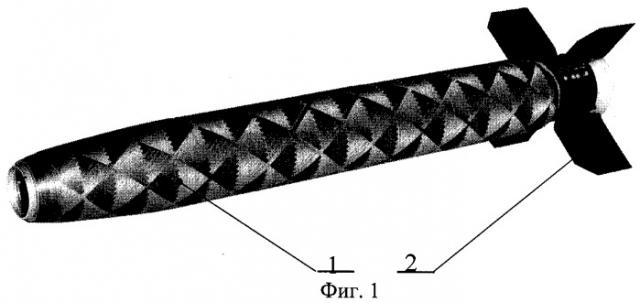
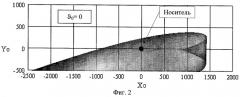
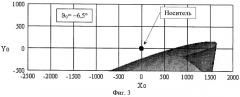
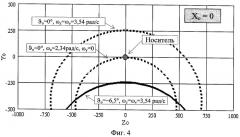
Изобретение поясняется графическим материалом, где на фиг.1 показан внешний вид стартовой ступени: позиция 1 - корпус двигателя, позиция 2 - блок стабилизатора. На фиг.2 приведена область возможных траекторий полета стартовой ступени относительно носителя для носителя, летящего со скоростью 300 м/с на высоте 500 м при угле пуска ракеты ϑ₀, превышающем допустимую величину ϑ_доп. На фиг.3 для тех же условий полета носителя приведена область возможных траекторий полета стартовой ступени при угле пуска ракеты ϑ₀ меньше допустимого ϑ_доп. На фиг.4 для носителя, летящего со скоростью 300 м/с на высоте 500 м, приведены возможные координаты Y_o, Z_o стартовой ступени относительно носителя, зафиксированные в момент прохождения стартовой ступенью вертикальной плоскости, проходящей через начало связанной системы координат носителя. На фиг.5 для того же режима полета носителя приведена траектория полета стартовой ступени относительно носителя при угле пуска ракеты ϑ₀, превышающем допустимую величину ϑ_доп. На фиг.6-7 показана зависимость траекторий движения стартовой ступени относительно носителя от скорости V_n и высоты Y_n полета носителя при постоянном угле пуска ракеты ϑ₀. На фиг.8 представлен график изолиний ϑ_доп в функции скорости V_n и высоты Y_n полета носителя.

Способ осуществляется следующим образом. На этапе проектирования для выбранного способа управления ракетой, для рабочего диапазона скоростей V_n и высот Y_n полета носителя, для заданного режима полета носителя (горизонтальный полет, пикирование, кабрирование) вычисляются значения допустимых углов пуска ракеты ϑ_доп=ϑ_n+ϑ_пк, где ϑ_n - угол тангажа носителя, ϑ_пк - угол поворота транспортно-пускового контейнера относительно продольной оси ОХ_n, связанной системы координат носителя, и заносятся в бортовую вычислительную систему (БВС) носителя в виде двумерного массива ϑ_доп=ϑ_доп(Y_n, Y_n). Допустимыми ϑ_доп считаются те углы, при которых все возможные траектории отделившейся стартовой ступени проходят ниже высоты полета носителя на заданном расстоянии ΔL_доп.

При обнаружении цели БВС сравнивает значение угла пуска ϑ₀=ϑ_n+ϑ_пк, необходимого для вывода ракеты на траекторию, обеспечивающую поражение цели, с допустимым ϑ_доп для текущих условий полета носителя и, в случае выполнения условия ϑ0≤ϑ_доп, дает разрешение на запуск ракеты.

Траектория движения отделившейся стартовой ступени относительно носителя зависит от скорости и высоты полета носителя, а также от начальных возмущений, которые получает стартовая ступень после разделения ступеней ракеты. Известно, что основным возмущающим фактором, влияющим на траекторию отделившейся стартовой ступени, является угловая скорость ω оси ракеты относительно поперечных осей [Известия ТулГУ, Сер. «Проблемы специального машиностроения», Вып.8 - Тула: ТулГУ, 2005, с.45-49]. В том случае, когда механизм разделения не создает дополнительных возмущений разделяющимся ступеням ракеты, величина и направление угловой скорости ω оси ракеты определяются характером управляемого движения перед разделением. При полете с постоянной или плавно меняющейся командой угловая скорость ω оси ракеты относительно поперечных осей практически равна нулю. Если на ракету мгновенно подается команда, обнуляется действующая команда или изменяется знак команды, то ось ракеты начинает колебаться вокруг центра масс с угловой скоростью ω. Составляющие максимальной угловой скорости ω по осям OY, OZ связанной системы координат ракеты равны: ω_{у max}=k_max·α_бал·2π·f₀, ω_{z max}=k_max·β_бал·2π·f₀, где k_max - коэффициент заброса при изменении знака команды; α_бал - балансировочный угол атаки, β_бал - балансировочный угол скольжения, f₀ - собственная частота ракеты. При максимальной угловой скорости ракеты относительно поперечной оси угол атаки (скольжения) близок к нулю.

В общем случае перед разделением ступеней ракеты угловая скорость ее оси может иметь любое значение в диапазоне ±ω_max.

Траектория полета отделившейся стартовой ступени относительно носителя определяется в процессе решения системы уравнений движения летательного аппарата [А.А.Лебедев, Л.С.Чернобровкин. Динамика полета беспилотных летательных аппаратов. - М., Машиностроение, 1973, с.467, уравнения с 1 по 12 системы уравнений (11.1) и С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. Механика полета. - М., Машиностроение, 1969, с.193, уравнения (4.135)] совместно с уравнениями движения носителя.

Выполняя вычисления во всем возможном диапазоне значений ±ω_max, получаем область возможных траекторий стартовой ступени относительно носителя. Если угол пуска ракеты превышает допустимую величину, то возможен случай, когда, по меньшей мере, одна из траекторий стартовой ступени пройдет через носитель.

Следовательно, для того чтобы исключить возможность столкновения носителя со стартовой ступенью, угол пуска ракеты должен быть таким, чтобы все возможные траектории полета стартовой ступени относительно носителя при любом возможном значении угловой скорости ω оси ракеты в диапазоне от минус ω_max до плюс ω_max проходили ниже носителя.

Моделированием траектории движения отделившейся стартовой ступени относительно носителя при максимальных значениях угловой скорости ω и различных углах пуска ϑ₀ определяется та допустимая величина угла пуска ϑ_доп, при которой траектории отделившейся стартовой ступени пройдут мимо носителя при любом возможном значении угловой скорости оси ракеты в момент разделения ступеней.

Пример 1

Носитель летит равномерно прямолинейно в режиме горизонтального полета со скоростью V_n, без крена и скольжения на постоянной высоте Y_n с углом тангажа ϑ_n. Диапазон изменения скорости полета носителя от 150 до 300 м/с. Диапазон изменения высоты полета носителя от 0 до 5000 м над уровнем моря. Зависимость угла тангажа ϑ_n носителя от скорости и высоты полета приведена в таблице 1.

Пусковая установка с ТПК может поворачиваться в вертикальной плоскости носителя относительно его продольной оси ОХ_n на угол ϑ_пк в диапазоне от 0 до минус 12°. При ϑ_пк=0° ось ТПК параллельна продольной оси носителя ОХ_n.

Таблица 1Угол тангажа носителя ϑn, град
Vn, м/с	Yn, м
0	3000	5000
150	5,0	8,4	10,8
200	3,1	4,3	5,5
250	2,1	2,7	3,6
300	2,0	2,6	3,5

В ТПК находится двухступенчатая осесимметричная ракета схемы «утка» с двухканальной системой управления, вращающаяся во время полета по крену за счет косо поставленного оперения.

В зависимости от угла поворота ПУ угол пуска ракеты ϑ₀=ϑ_n+ϑ_пк может изменяться от 10,8° при ϑ_пк=0° (V_n=150 м/с, Y_n=5000 м, ϑ_n=10,8°) до минус 10° при ϑ_пк=12°(V_n=300 м/с, Y_n=0 м, ϑ_n=2,0°).

После начала работы стартового двигателя (t=0 с) под действием тяги стартового двигателя ракета перемещается по нарезам контейнера и к моменту t_cx выхода из контейнера (t_cx=0,2 с) получает продольную скорость V_cx, равную 30 м/с, и угловую скорость крена ω_х, равную 5 об/с.

После выхода ракеты из контейнера автономная система управления ракеты стабилизирует ее траекторию относительно заданного направления стрельбы и к моменту разделения угол ϑ_р тангажа ракеты равен углу пуска ϑ₀.

В зависимости от скорости и высоты полета носителя над уровнем моря скорость ракеты перед разделением соответствует числам Маха от 3,0 до 4,5. Значения балансировочного угла атаки α_бал и собственной частоты ракеты f₀ для различных чисел Маха и высот над уровнем моря приведены в таблице 2. Здесь же представлены значения максимальной угловой скорости оси ракеты ω_max=k_max·α_бал·2π·f₀ при коэффициенте заброса ракеты k_max=2.

В общем случае при разделении ступеней ракеты угловая скорость ее оси в канале отклонения рулей может иметь любое значение в диапазоне ±ω_max. При ω=ω_max угол атаки не превышает α_бал.

Таблица 2
М	αбал	Y, м
0	1000	2000	3000	4000	5000
f0	ωmax	f0	ωmax	f0	ωmax	f0	ωmax	f0	ωmax	f0	ωmax
град	Гц	рад/с	Гц	рад/с	Гц	рад/с	Гц	рад/с	Гц	рад/с	Гц	рад/с
3.0	2.0	7.8	3.4	7.4	3.2	6.9	3.0	6.5	2.9	6.1	2.7	5.7	2.5
3.5	1.9	8.4	3.5	8.0	3.3	7.5	3.1	7.1	3.0	6.6	2.8	6.2	2.6
4.0	1.9	8.8	3.7	8.4	3.5	7.9	3.3	7.4	3.1	6.9	2.9	6.5	2.7
4.5	1.8	9.5	3.8	9.0	3.6	8.5	3.4	8.0	3.2	7.5	3.0	7.0	2.8

Для расчета траектории движения отделившейся стартовой ступени используем приведенную ниже аэробаллистическую модель.

Аэробаллистическая модель движения стартовой ступени

1. Уравнения движения стартовой ступени

Динамические уравнения движения центра масс СС:

Кинематические уравнения движения центра масс СС:

Динамические уравнения вращательного движения СС вокруг центра масс:

Кинематические уравнения вращения СС вокруг центра масс:

Значения углов α_т, β_т и γ_а определяются из следующих уравнений:

При безветрии воздушная скорость СС V равна земной скорости СС Y_к, а углы атаки α, скольжения β равны, соответственно, траекторному углу атаки α_т и траекторному углу скольжения β_т. При наличии ветра и известных проекциях скорости ветра W_x, W_y, W_z на оси местной географической системы координат, воздушная скорость и углы атаки, скольжения СС определяются по зависимостям:

2. Аэродинамические силы и моменты, действующие на стартовую ступень

Составляющие аэродинамических сил и моментов в проекциях на оси, связанной с фюзеляжем системы координат OXYZ, продольная ось ОХ которой направлена вдоль оси фюзеляжа, определяются по формулам:

Х=-C_x·q·S_x,

Y=C_y·q·S_x,

Z=-C_z·q·S_x,

M_x=m_x·q·S_x·L_x,

M_y=m_y·q·S_x·L_x,

M_z=m_z·q·S_x·L_x,

где ρ - плотность воздуха; V - скорость стартовой ступени;

S_x - характерная площадь. S_x=0,0133 м²;

L_x - характерная длина. L_x=1 м;

С_х, С_у, C_z - коэффициенты составляющих аэродинамической силы (продольной, нормальной и поперечной, соответственно) по осям связанной системы координат OXYZ;

m_x, m_y, m_z - коэффициенты составляющих аэродинамического момента по осям связанной системы координат OXYZ.

Коэффициент сопротивления С_х вычисляется по формуле:

Значения коэффициентов С_хСС и η_M в функции числа М приведены в таблице 3.

F_фСС=π·D_фСС·L_Фсс.

D_{ф CC} - диаметр фюзеляжа стартовой ступени. D_{ф CC}=0,170 м;

L_{ф CC} - длина фюзеляжа стартовой ступени. L_{ф CC}=1,454 м.

Δ(2с_f)_M=0=(2 с_f)_M=0(Н)-(2 с_f)_M=0(Н=0).

Значения коэффициентов (2с_f)_M=0 в функции числа Рейнольдса (Re) приведены в таблице 4, число Re вычисляется по формуле:

ν - кинематическая вязкость воздуха. Значения ν в функции высоты над уровнем моря Н приведены в таблице 5.

Коэффициенты нормальной C_y и поперечной С_z силы равны:

C_у=С_{у ф}+С_{у ст},

C_z=C_{z ф}+С_{z ст}.

Коэффициенты нормальной и поперечной силы фюзеляжа стартовой ступени:

Значения С_{n ф CC} (М,α) и С_{n ф CC} (М,β) приведены в таблице 6; α и β - углы атаки и скольжения, град;

Коэффициенты нормальной и поперечной силы стабилизатора:

Значения С_{n ст}(М,α) и С_{n ст}(М,β) в функции числа Маха и угла атаки стабилизатора приведены в таблице 8.

Значения коэффициентов интерференции стабилизатора К_{α ст} приведены в таблице 10.

Коэффициенты момента крена:

δ_ст - угол установки консолей стабилизатора δ_ст=0,25°.

Значения производных коэффициентов момента крена в функции числа Маха приведены в таблице 11.

Относительная угловая скорость крена равна:

где ω_х - угловая скорость крена, рад/с.

Коэффициенты моментов рыскания и тангажа:

m_у=m_уф+m_{у ст},

m_z=m_{z ф}+m_{z ст}.

Коэффициенты моментов рыскания и тангажа фюзеляжа стартовой ступени:

Х_т - положение центра тяжести стартовой ступени. x_т=0,812 м.

Координаты точек приложения поперечной и нормальной силы x_{dz ф}, x_{dy ф}, определяются по зависимостям:

Значения относительного центра давления фюзеляжа стартовой ступени и приведены в таблице 7.

Коэффициенты демпфирующих моментов m_{у ф}(ω_у) и m_{z ф}(ω_z) вычисляются по формулам:

Здесь (С_{z ф})*=(С_{у ф})*=С_{у ф}(М,α=1°),

ω_у, ω_z - проекции вектора угловой скорости стартовой ступени на оси OY, OZ связанной системы координат, 1/рад.

Коэффициенты моментов рыскания и тангажа стабилизатора:

Координаты точек приложения сил х_{dу ст} и х_{dz ст}:

х_ст - расстояние от носка ракеты до бортовой хорды стабилизатора. х_ст=1,279 м,

b_{б ст} - длина бортовой хорды стабилизатора. b_{б ст}=0,15 м. Значения центра давления стабилизатора приведены в таблице 9.

Коэффициенты демпфирующих моментов m_{у ст}(ω_у) и m_{z ст}(ω_z) равны:

Здесь (C_{z ст})^*=(С_{у ст})^*=С_{у ст}(М,α=1°).

3. Начальные условия

Механизм разделения ступеней ракеты не создает разделяющимся ступеням дополнительных возмущений, поэтому начальные условия движения СС (V_{CC 0}, θ_{СС 0}, Ψ_{СС 0}, х_{СС 0}, у_{СС 0}, z_{СС 0}, ω_{x СС 0}, ω_{у СС 0},ω_{z CC 0}, ϑ_{CC 0}, ψ_{CC 0}, γ_{CC 0}) практически равны тем значениям параметров движения, которые имела ракета перед разделением. Проекции угла вектора скорости отделившейся СС изменяются на величину

где V_p - скорость ракеты перед разделением, V_{y CC}=Δх_т·ω_z, V_{z CC} =Δх_т·ω_у, Δх_т - расстояние между центрами масс ракеты и СС перед разделением (Δх_т=1.284 м), ω_z, ω_у - коэффициенты моментов рыскания и тангажа ракеты перед разделением.

4. Исходные данные

Таблица 3
М	0,0	0,6	0,7	0,8	0,9	1,0	1,1	1,2
Сх0 СД	0,836	0,836	0,850	0,882	0,915	1,226	1,228	1,303
ηМ	1,000	0,950	0,945	0,935	0,925	0,915	0,905	0,890
Продолжение таблицы 3
М	1,3	1,5	1,7	2,0	2,5	3,0	4,0	5,0
Сх0 СД	1,317	1,329	1,325	1,283	1,233	1,198	1,129	1,081
ηМ	0,880	0,840	0,815	0,765	0,700	0,640	0,520	0,420
Таблица 4Удвоенный коэффициент трения плоской пластины
Re	0	1·106	2·106	3·106	4·106	5·106	7·106	1·107	2·107	3·107
(2сf)M=0	0,00900	0,00900	0,00790	0,00730	0,00695	0,00673	0,00637	0,00596	0,00540	0,00505
Продолжение таблицы 4
Re	4·107	5·107	7·107	1·108	2·108	3·108	4·108	5·108	1·109	1·1010
(2сf)М=0	0,00483	0,00469	0,00449	0,00424	0,00382	0,00361	0,00349	0,00344	0,00320	0,00320
Таблица 5Кинематическая вязкость воздуха
Y, км	-0.5	0	2.5	5.0	7.5	10.0	12.5
ν, м2/с	0,0000141	0,0000146	0,0000179	0,0000221	0,0000277	0,0000352	0,0000495
Продолжение таблицы 5
Y, км	15.0	17.0	20.0	25.0	30.0	35.0	90.0
ν, м2/с	0,0000730	0,0001084	0,0001600	0,0003500	0,0008356	0,0011661	0,0157590

Таблица 6Коэффициенты Сn ф СС(М,α) нормальной силы фюзеляжа ССЕсли β=α, то Сn ф CC(М,β)=Сn ф CC(М,α)Cn ф СС((М,(α<0))=-Сn ф CC(М,(α>0))
М	α, град
0	2	4	6	8	10	12	14	16	18	20	89
00.60.70.80.91.01.11.21.31.72.02.53.04.05.0	000000000000000	0.1300.1310.1310.1310.1320.1370.1440.1470.1500.1570.1640.1710.1760.1760.169	0.2790.2810.2820.2830.2850.2950.3070.3150.3190.3360.3490.3640.3750.3790.374	0.4470.4510.4520.4540.4570.4720.4920.5030.5110.5380.5590.5880.6130.6650.704	0.6330.6400.6420.6460.6510.6720.6990.7150.7260.7690.8040.8680.9611.0841.093	0.8370.8480.8530.8600.8680.8950.9290.9520.9711.0381.1141.2971.4521.5381.511	1.0571.0781.0861.0951.1071.1431.1921.2251.2511.3901.5751.8541.9812.0211.962	1.2921.3271.3391.3531.3761.4271.4881.5321.5821.8972.1862.4422.5372.5302.447	1.5421.5961.6131.6421.6781.7421.8221.9172.0142.5562.8563.0573.1213.0712.985	1.8051.8841.9181.9622.0102.1062.2522.4182.5953.2863.5323.6933.7203.6463.538	2.0802.1952.2522.3112.3912.5612.8113.0693.3434.0314.2384.3464.3504.2704.111	18.58423.30724.36524.71724.54224.36924.10823.84523.75822.93422.44322.44622.44822.44722.442
Таблица 7Положение центра давления фюзеляжа СС в долях длины фюзеляжаОтсчитывается от носка корпусаЕсли β=α, то
М	α, град
0	2	4	6	8	10	12	14	16	18	20	89
00,60,70,80,91,01,11,21,31,72,02,53,04,05,0	0,1170,1180,1190,1190,1210,1240,1290,1310,1340,1440,1530,1690,1860,2160,234	0,1340,1350,1360,1360,1380,1400,1440,1460,1480,1570,1660,1810,1970,2260,245	0,1650,1660,1660,1670,1680,1690,1720,1730,1750,1830,1910,2050,2210,2510,276	0,1910,1930,1930,1940,1950,1960,1970,1980,2000,2080,2150,2310,2490,2970,334	0,2150,2170,2170,2180,2200,2200,2220,2220,2240,2330,2420,2640,2970,3450,366	0,2350,2380,2400,2410,2430,2430,2440,2450,2480,2590,2750,3130,3430,3710,386	0,2540,2580,2600,2620,2640,2650,2670,2680,2720,2920,3190,3540,3700,3890,400	0,2710,2770,2790,2810,2840,2860,2880,2900,2960,3330,3590,3790,3890,4020,412	0,2860,2940,2960,3000,3050,3070,3090,3160,3260,3690,3860,3960,4020,4130,423	0,3000,3100,3140,3190,3230,3270,3340,3450,3580,3940,4030,4090,4130,4220,431	0,3130,3250,3300,3350,3420,3500,3620,3740,3870,4120,4170,4200,4220,4310,439	0,5510,5530,5530,5530,5530,5530,5530,5530,5530,5530,5530,5530,5530,5530,553

Таблица 8Коэффициенты Сn ст(М,α) нормальной силы изолированного стабилизатораОтнесены к площади двух консолей стабилизатораЕсли β=α, то Сn ст(М,β)=Сn ст (М,α)Сn ст(М,(α<0))=-Сn ст М,(α>0))
α, град	М
0	0,6	0,7	0,8	0,9	1,0	1,1	1,3	1,5	1,7	2,0	2,5	3,0	4.0	5,0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
20	0,996	1,084	1,124	1,174	1,248	1,416	1,298	1,122	0,986	0,864	0,742	0,572	0,494	0,360	0,284
Таблица 9Положение центра давления стабилизатора в долях бортовой хорды.Отсчитывается от начала передней кромки стабилизатора.Если β=α, то
α,град	М
0	0,6	0,7	0,8	0,9	1,0	1,1	1,3	1,5	1,7	2,0	2,5	3,0	4,0	5,0
0	0,298	0,291	0,285	0,276	0,264	0,304	0,460	0,534	0,556	0,562	0,559	0,554	0,551	0,547	0,543
20	0,298	0,291	0,285	0,276	0,264	0,304	0,460	0,534	0,556	0,562	0,559	0,554	0,551	0,547	0,543
Таблица 10
Коэффциенты интереренции стабилизатора
М	о	0,6	0,7	0,8	0,9	1,0	1,1	1,3	1,5	1,7	2,0	2,5	3,0	4,0	5,0
Кα ст	1,81	1,81	1,81	1,81	1,81	1,81	1,77	1,69	1,62	1,55	1,45	1,32	1,24	1,17	1,15
Кα ст	1,32	1,32	1,32	1,32	1,32	1,32	1,32	1,32	1,32	1,30	1,26	1,20	1,16	1,13	1,13
Таблица 11Коэффициенты момента крена
М	0	0.6	0.7	0.8	0.9	1.0	1.1	1.2
, l/град	0,0307	0,0307	0,0314	0,0323	0,0335	0,0365	0,0368	0,0358
, l/рад	-0,527	-0,527	-0,540	-0,555	-0,576	-0,627	-0,633	-0,614
Продолжение таблицы 11
М	1,3	1,5	1,7	2,0	2,5	3,0	4,0	5,0
, 1/град	0,0348	0,0323	0,0299	0,0266	0,0215	0,0187	0,0140	0,0148
, 1/рад	-0,598	-0,560	-0,514	-0,457	-0,370	-0,321	-0,279	-0,279

Решая приведенную выше систему уравнений движения стартовой ступени, определяем ее координаты х, у и z в стартовой системе координат, положение которой относительно земли зафиксировано в момент начала работа стартового двигателя, а начало находится в центре масс ракеты в ТПК.

При равномерном прямолинейном полете носителя его координаты в момент времени t в стартовой системе координат в общем случае определяются по зависимостям:

x_n=V_n·(t-t_cx)·cosθ·cosΨ_n;

y_n=V_n·(t-t_cx)·sinθ_n;

z_n=-V_n·(t-t_cx)·cosθ_n·sinΨ_n.

В рассматриваемом примере носитель находится в режиме горизонтального полета и после пуска ракеты не меняет направление полета. В этом случае θ_n=Ψ_n=0 и в стартовой системе координат в момент времени t

x_n=V_n·(t-t_cx);

у_n=z_n=0.

Координаты ракеты относительно носителя в момент времени t равны:

x_O=x-x_n;

у_о=y-y_n;

z_o=z-z_n.

Введем понятие «критерия безопасности» - минимального допустимого расстояния между носителем и отделившейся стартовой ступенью

Зададим значение «критерия безопасности» равным 100 м.

ϑ_доп, град

Таблица 12
Vn, м/с	Yn, м
0	500	1000	1500	2000	2500	3000	3500	4000	4500	5000
150	21,4	21,7	22,0	22,4	22,6	22,7	22,9	23,1	23,2	23,5	23,9
200	9,2	9,2	8,8	8,7	8,4	8,1	7,8	7,8	7,8	8,0	8,3
210	7,4	7,2	6,9	6,6	6,2	5,8	5,5	5,4	5,4	5,6	6,0
220	5,7	5,3	5,0	4,7	4,2	3,8	3,5	3,3	3,3	3,5	3,9
230	4,2	3,7	3,3	2,9	2,4	1,9	1,6	1,4	1,4	1,7	2,0
240	2,7	2,3	1,8	1,3	0,7	0,2	-0,1	-0,3	-0,3	0,0	0,2
250	1,4	0,9	0,3	-0,2	-0,9	-1,4	-1,7	-1,8	-1,7	-1,5	-1,3
260	0,2	-0,4	-1,0	-1,6	-2,3	-2,7	-3.1	-3,2	-3,0	-2,8	-2,6
270	-0,9	-1,6	-2,1	-2,9	-3,5	-3,9	-4,3	-4,3	-4,2	-4,0	-3,7
280	-1.9	-2,6	-3,3	-4,0	-4,6	-5,1	-5,4	-5,3	-5.3	-5,0	-4,7
290	-3,0	-3,6	-4,4	-5,1	-5,6	-6,2	-6,3	-6,3	-6,2	-5,9	-5,5
300	-3,9	-4,6	-5,4	-6,0	-6,6	-7,0	-7,1	-7,1	-7,0	-6,7	-6,3

Вычисляя траектории полета отделившейся стартовой ступени относительно носителя при различных значениях угла пуска ракеты ϑ₀, определяем то минимальное значение - допустимый угол пуска ϑ_доп - при котором вся совокупность возможных траекторий проходит ниже носителя на расстоянии L_o≥L_min.

Результаты расчета приведены в таблице 12.

Значения ϑ_доп=ϑ_доп(V_n, Y_n) вводятся в бортовую вычислительную систему носителя, которая дает разрешение на запуск ракеты, если требуемый угол пуска не превышает допустимый.

Пример 2

Для носителя и ракеты из примера 1 рассмотрим частный случай.

Носитель летит равномерно прямолинейно в режиме горизонтального полета без крена и скольжения. V_n=300 м/с, Y_n=500 м, ϑ_n=2,1°.

Перед носителем находятся две цели.

Для поражения первой цели ракету нужно запустить под углом ϑ₀=ϑ_n+ϑ_пк=0°, для поражения второй цели - под углом ϑ₀=ϑ_n+ϑ_пк=-6,5°.

Исходя из условий безопасности, угол пуска ракеты при V_n=300 м/с, Y_n=500 м не должен превышать ϑ_доп=-4,6° (таблица 12). Следовательно, ракета должна быть запущена по второй цели.

Посмотрим, что может произойти, если ракета будет запущена по первой цели под углом пуска ϑ₀=0°.

В момент разделения ступеней параметры движения ракеты следующие: V=1305 м/с (М=3,82), θ=-0,9°, Ψ=0, х=1323 м, у=-11 м, z=0, ω_х=10,5 об/с, ω_у=0, ω_z=2,34 рад/с, ϑ=0, ψ=0, γ=-2,5°).

Отделившаяся стартовая ступень имеет те же начальные параметры движения, что ракета перед разделением, за исключением проекций угла вектора скорости, которые изменятся на величину

Решая приведенную выше систему уравнений движения, получаем траекторию полета стартовой ступени относительно носителя, которая в координатах x_o, sign(l_o)=sign(y_o) приведена на фиг.5. При x_о=0 расстояние l_о между носителем и стартовой ступенью равно нулю: происходит столкновение носителя со стартовой ступенью.

Попутно заметим, что в момент разделения ступеней ракета может иметь любые значения угловых скоростей ω_у, ω_z в диапазоне от минус 3,54 рад/с до плюс 3,54 рад/с (таблица 2), а угол крена ракеты γ - любое значение в диапазоне от 0 до 360°. Координаты стартовой ступени относительно носителя в момент прохождения стартовой ступенью вертикальной плоскости, проходящей через начало связанной системы координат носителя, при ω_у=ω_z=3,54 рад/с для значений γ от 0 до 360° приведены на фиг.4. Здесь же приведен график для варианта ω_у=0, ω_z=2,34 рад/с и γ от 0 до 360°.

Из рисунка видно, что при запуске ракеты под углом ϑ₀, величина которого превышает ϑ_доп, найдется по меньшей мере одна траектория полета стартовой ступени, проходящая через носитель.

При запуске ракеты по второй цели под углом ϑ₀=ϑ_n+ϑ_пу=-6,5°, величина которого меньше ϑ_доп=-4,6°, все возможные траектории полета стартовой ступени пройдут ниже носителя (фиг.3, 4).

Конструкция ракеты, реализующей этот способ, подобна той, которая входит в состав многоцелевого ракетного комплекса «Гермес», представленного на выставке IDEX-2005 [Рынки вооружений, АРМС-ТАСС, 2005, №1-2, с.6-9]. В этой конструкции управление ракетой осуществляется сразу же после выхода ракеты из ТПК, а стартовый двигатель отделяется после того, как разгоняет ракету до максимальной скорости. У таких ракет стартовая ступень, отделяющаяся после окончания работы стартового двигателя, представляет собой аэродинамически устойчивое оперенное тело вращения большого удлинения. Аналогичная конструкция стартовой ступени описана в изобретении RU 2202761. Механизм разделения ступеней, конструкция которого подобна описанной в изобретении RU 2233424, не создает дополнительных возмущений разделяющимся ступеням ракеты.

Представленный способ пуска двухступенчатой управляемой ракеты с воздушного носителя позволяет исключить столкновение отделившейся стартовой ступени с носителем при любых возможных управляющих командах в момент разделения ступеней ракеты.

Способ запуска двухступенчатой управляемой ракеты с воздушного носителя, включающий пуск ракеты с помощью стартового двигателя из транспортно-пускового контейнера (ТПК), размещенног