Способ измерения скорости линейного перемещения объекта

Способ измерения скорости линейного перемещения объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может быть использовано для измерения скорости линейного перемещения объектов по заданной траектории.

Известен способ измерения скорости движения объекта [авт. свид. СССР №1672378, кл. G01Р 3/64, БИ №31, 1991], который основан на времяпролетном принципе измерения и использовании датчиков положения, установленных вдоль траектории движения, предварительном формировании и запоминании эталонной функции как отношения зависимостей от координаты местоположения объекта выходных напряжений двух соседних датчиков положения, измерении текущих значений напряжений этих датчиков в процессе движения объекта, определении текущей функции от времени отношения этих напряжений, сравнении значений эталонной и текущей функций, определении и запоминании моментов времени t_i равенства значений текущей функции заданным значениям эталонной функции, определении по эталонной функции значений координат X_i положения объекта, задании их в качестве точек Δt_i=t_i-t_i-1 регистрации, соответствующих упомянутым моментам, вычислении интервалов времени Δt_i=t_i-t_i-1 прохождения объектом расстояния Δх_i между соседними точками регистрации X_i-1 и X_i и определении значений средней скорости на интервале пути Δх_i по формуле

где Δx_i=X_i-X_i-1 - соответственно, интервал пути и интервал времени между моментами регистрации t_i и t_i-1; i=1, 2, ..., N-1; N - количество точек регистрации.

Согласно данному способу путем разбиения основного интервала между двумя соседними датчиками на достаточно большое количество (N-1) малых подинтервалов, ограниченных с обеих сторон заданными заранее точками (координатами) регистрации, можно достигнуть резкого уменьшения методической погрешности измерения скорости за счет уменьшения базового расстояния Δx_i=X_i-X_i-1 при вычислении скорости по формуле

и приближении тем самым измеренного значения скорости к мгновенному.

В данном способе одновременно со снижением методической составляющей погрешности измерения скорости резко возрастает относительная инструментальная составляющая погрешности, так как относительное значение погрешности измерения интервала пути (времени) увеличивается с уменьшением этих интервалов при использовании того же измерительного инструментария. Таким образом, уменьшение расстояния между задаваемыми точками регистрации, с одной стороны, приводит к уменьшению методической погрешности измерения скорости, а с другой стороны, - к увеличению относительной инструментальной погрешности измерения интервалов пути и времени, а в конечном итоге - к снижению эффекта от уменьшения расстояния между точками регистрации. Данный способ хотя и обеспечивает измерение почти мгновенных значений скорости, но с большой погрешностью из-за резкого увеличения доли относительной инструментальной погрешности.

Известен способ измерения скорости линейного перемещения объекта, являющийся наиболее близким техническим решением к заявляемому (прототипом) [Патент на изобретение Российской Федерации №2208794, кл. G01Р 3/64, БИ №20, 2003], который также основан на использовании датчиков положения, установленных вдоль траектории движения, предварительном формировании и запоминании эталонной функции как отношения зависимостей от координаты местоположения объекта выходных напряжений двух соседних датчиков положения, измерении текущих значений напряжений этих датчиков в процессе движения объекта, определении текущей функции от времени отношения этих напряжений, сравнении значений эталонной и текущей функции, определении и запоминании моментов времени t_i равенства значений текущей функции заданным значениям эталонной функции, определении по эталонной функции значений координат X_i положения объекта, задании их в качестве точек Δt_i=t_i-t_i-1 регистрации, соответствующих упомянутым моментам, вычислении интервалов времени Δt_i=t_i-t_i-1 прохождения объектом расстояния Δx_i между соседними точками регистрации X_i-1 и X_i и определении значений средней скорости на интервале пути Δx_i по формуле

где Δx_i=Х_i-X_i-1 и Δt_i - соответственно, интервал пути и интервал времени между моментами регистрации t_i и t_i-1; i=1, 2, ... N-1; N - количество точек регистрации, причем при задании координат X_i регистрации с шагом Δx_i интервал пути Δx₁ между первым и вторым моментами регистрации, соответствующими координатам Х₂ и Х₁ местоположения объекта, определяют по формуле

а интервалы пути Δx_i между последующими моментами регистрации определяют по формуле

где σ_M1 - среднеквадратическое отклонение методической погрешности на 1-м интервале пути между соседними точками регистрации объекта;

- закон изменения отношения среднеквадратических отклонений методической погрешности σ_Mi+1 на (i+1)-м и σ_Mi на i-м интервале пути между соседними точками регистрации объекта; σ_x - среднеквадратическое отклонение инструментальной погрешности задания координаты регистрации объекта; σ_t - среднеквадратическое отклонение инструментальной погрешности измерения интервала времени Δt; Δt_i-1 - время прохождения объектом интервала пути Δx_i-1 между двумя соседними точками регистрации, предшествующего интервалу пути Δх_i, на котором вычисляется текущее значение скорости V_i.

Недостатком данного способа измерения скорости линейного перемещения объекта является ограниченная область его использования, поскольку в нем невозможно достичь предельное значение точности измерения скорости при полной минимизации суммы методической и инструментальной составляющих погрешности измерения скорости только за счет уменьшения интервала измерения скорости Δx.

Анализ процесса измерения, приведенный в описании способа-прототипа, был проведен для точечного объекта регистрации, что и определяет недостаток данного способа измерения, сводящийся к ограниченным функциональным возможностям.

При решении задач управляемого разгона реальными объектами, например, в электродинамических ускорителях масс (ЭДУМ), эти объекты имеют обычно протяженные размеры (плазменный сгусток) и распределенные по объему параметры. Естественно уменьшение интервала измерения приводит к нарушению условия точечности объекта разгона, а это приводит к необходимости использовать модель объекта с распределенными параметрами. При этом сохраняется требование необходимости иметь точную информацию о скорости объекта в реальном времени в процессе разгона для формирования команд управления подводом энергии к ускорителю масс и, особенно, на конечном участке контролируемой траектории движения. Кроме этого, анализ данного типа систем управления [Исследование устойчивости системы стабилизации плазмы с учетом характеристик реальных звеньев / Е.С.Паславский // Управление объектами с распределенными параметрами. - Киев: Институт кибернетики АН УССР. - 1979. - С.55-67] показал нестационарность объекта управления. В итоге это приводит к тому, что сила , прикладываемая к объекту в ЭДУМ, является случайной функцией, распределенной по объему разгоняемого объекта. Следовательно, скорость движения разгоняемого объекта тоже случайная функция и определяется проекцией по направлению движения объекта совокупной (интегрированной по объему) силы. Таким образом, распределенная модель разгоняемого объекта приводит к необходимости усреднения этой функции силы на интервале Т_у

где f() - функциональная зависимость между силой и скоростью разгоняемого объекта.

Выражение (2) определяет условия детерминированного управления средней скорости разгоняемого объекта. Причем из этого выражения можно сделать вывод о том, что время усреднения Т_у управляющего воздействия определяет и время осреднения измеряемой величины скорости и если усреднять скорость на интервале времени, меньшем интервала времени Т_y, то процесс детеминированного управления скоростью будет нарушен. Данный вывод согласуется с известным принципом двойственности измерения и управления.

Интервал усреднения (в координатном измерении) разгоняющей силы определяется интервалом неопределенности в поведении плазмы, который определяется геометрическими параметрами разгоняемого плазменного сгустка. А поскольку измерение скорости производится по одной координате, то интервал усреднения разгоняющей силы не должен быть меньше максимальной длины плазменного сгустка Δх_пл. Из данных рассуждении можно сделать вывод о том, что при измерении скорости движения разгоняемого в рассматриваемой системе объекта существует предельная минимальная величина базового расстояния измерения скорости, на которой возможно пропорциональное управление скоростью движения объекта. В противном случае нарушается уравнение (2) и, следовательно, детерминированное управление невозможно.

Задачей изобретения является расширение функциональных возможностей способа путем повышения точности измерения скорости за счет создания условий, приводящих к минимизации суммы методической и инструментальной составляющих погрешности измерения скорости. Указанные условия создаются путем выбора и задания непосредственно в процессе измерения не только вполне определенных (оптимальных) интервалов пути между соседними точками (координатами) регистрации на контролируемом участке траектории движения объекта, обеспечивающих минимизацию суммарной погрешности измерения, но и путем выбора и задания непосредственно в процессе измерения частоты опорного генератора.

Решение задачи достигается тем, что в способе измерения скорости движения объекта, основанном на использовании датчиков положения, установленных вдоль траектории движения, предварительном формировании и запоминании эталонной функции как отношения зависимостей от координаты местоположения объекта выходных напряжений двух соседних датчиков положения, измерении текущих значений напряжений этих датчиков в процессе движения объекта, определении текущей функции от времени отношения этих напряжений, сравнении значений эталонной и текущей функций, определении и запоминании моментов времени t_i равенства значений текущей функции заданным значениям эталонной функции, определении по эталонной функции значений координат X_i положения объекта, задании их в качестве точек Δt_i=t_i-t_i-1 регистрации, соответствующих упомянутым моментам, вычислении интервалов времени Δt=t_i-t_i-1 прохождения объектом расстояния Δx_i между соседними точками регистрации X_i-1 и X_i и определении значений средней скорости на интервале пути Δx_i по формуле

где Δx_i=X_i-X_i-1 - соответственно, интервал пути и интервал времени между моментами регистрации t_i и t_i-1; i=1, 2, ..., N-1; N - количество точек регистрации, при задании координат X_i регистрации с шагом Δx_i интервал пути Δx₁ между первым и вторым моментами регистрации, соответствующими координатам X₂ и Х₁ местоположения объекта, определяют по формуле

а интервалы пути Δx_i между последующими моментами регистрации определяют по формуле

где σ_M1 - среднеквадратическое отклонение методической погрешности на 1-м интервале пути между соседними точками регистрации объекта;

i=2, 3, N-1 - закон изменения отношения среднеквадратических отклонений методической погрешности σ_Mi+1 на (i+1)-м и σ_Mi на интервале пути между соседними точками регистрации объекта; σ_x - среднеквадратическое отклонение инструментальной погрешности задания ординаты регистрации объекта; σ_t - среднеквадратическое отклонение инструментальной погрешности измерения интервала времени Δt; Δ_t-1 - время прохождения объектом интервала пути Δx_i-1 между двумя соседними точками регистрации, предшествующего интервалу пути Δх_i, на котором измеряется текущее значение скорости V_i, причем полученный результат Δx_i дополнительно сравнивается с заданным интервалом Δx₀, кратным длине разгоняемого объекта, и если Δx_i>Δх₀, то на данном интервале Δx_i вычисляется текущее значение скорости V_i, а при условии Δx_i≤Δx₀ на начальном интервале измерения скорости по формуле

определяется период Т₁ такта измерения интервала времени Δt₁, а в общем случае по формуле

определяют период T_i такта измерения интервала времени Δt_i, измеряют временной интервал и для интервала Δх₀ вычисляют текущее значение скорости V_i.

Заявляемое решение отличается от способа-прототипа тем, что полученный результат Δx_i дополнительно сравнивается с заданным интервалом Δх₀ кратным длине разгоняемого объекта и если Δx_i>Δх₀, то на данном интервале Δx_i измеряется текущее значение скорости V_i, а при условии Δx_i≤Δх₀ на начальном интервале измерения скорости по формуле

определяется период Т₁ такта измерения интервала времени Δt₁, а в общем случае по формуле

определяют период Т_i такта измерения интервала времени Δt_i, измеряют временной интервал и на интервале Δх₀ вычисляют текущее значение скорости V_i.

Сравнение заявляемого технического решения с прототипом позволяет установить соответствие его критерию "новизна".

В соответствии с предлагаемым способом для определения условий измерений, обеспечивающих снижение общей погрешности измерения скорости, необходимо учитывать, кроме относительной методической погрешности γ_M, составляющие относительной погрешности измерения средней скорости, зависящие от Δx, а значит и от количества n контролируемых интервалов траектории и количества N точек регистрации при заданной длине S контролируемого участка траектории движущегося объекта. К составляющим относительной погрешности измерения средней скорости относится, во-первых, приведенная относительная погрешность γ_x измерения интервала Δx пути (погрешность из-за неточности задания точек регистрации на траектории движения)

где Δ_x - абсолютное значение погрешности измерения интервала Δx.

Второй составляющей погрешности измерения средней скорости является приведенная относительная погрешность γ_t измерения временного интервала Δt_i

где Δ_t - абсолютное значение погрешности измерения времени на i-м интервале Δx.

Учитывая, что при оценке погрешностей измерения скорости прямолинейного движения необходимо в качестве расчетного режима рассматривать равноускоренное движение [статья: Кириевский Е.В., Михайлов А.А. Выбор расчетного режима для оценки методической погрешности измерителей скорости времяпролетного типа // Известия Сев.-Кавк. научн. центра высш. шк., сер. "Техн. науки", №3-4, 1993, с.92-98], значение методической погрешности измерения на i-м интервале траектории принимаем равным величине аΔt_i/2, откуда можно представить относительную приведенную методическую погрешность γ_Mi на i-м интервале как:

где V_{cp i} - средняя скорость на i-ом интервале траектории.

Как отмечалось выше, из выражений (3)-(5) видно, что величины обеих составляющих инструментальной погрешности прямо пропорциональны, а величина методической погрешности обратно пропорциональна количеству интервалов n=N-1 на контролируемом участке пути. Тогда, выбирая в качестве критерия оптимальности интервала пути Δx минимум суммы методической и инструментальной погрешности измерения скорости, можно определить удовлетворяющие этому критерию значения Δx, n, N.

Более строгий подход предполагает учет случайного характера соответствующих погрешностей. Прологарифмируем и продифференцируем по времени t левую и правую части формулы (1) для средней скорости, в которой для простоты опустим индексы при Δt и V_cp:

Отсюда после несложных преобразований получаем

или, полагая, что погрешности достаточно малы и поэтому допускается переход от дифференциалов к соответствующим приращениям, получаем общее выражение для относительной погрешности косвенного измерения среднего значения скорости

Как видно из (6), относительная погрешность измерения средней скорости состоит из двух составляющих: погрешности Δ_x/Δx задания точек (координат) регистрации на траектории движения и погрешности Δ_t/Δt определения момента времени для каждого из концов временного интервала Δt_i.

Выражение (6) для относительной погрешности косвенного измерения среднего значения скорости имеет вид

где σ_и, σ_x, σ_t - соответственно, с.к.о. погрешности измерения средней на интервале скорости, с.к.о. погрешности измерения интервала пути и с.к.о. погрешности измерения времени.

Кроме с.к.о. составляющей погрешности измерения среднего значения скорости σ_и введем в рассмотрение с.к.о. методической составляющей погрешности измерения скорости σ_M. После возведения в квадрат левой и правой частей уравнения (7), добавления в левую и правую части полученного уравнения слагаемого извлечения квадратного корня из левой и правой последнего уравнения, получим:

В левой части уравнения (8) числитель представляет собой характеристику случайной погрешности измерения скорости, состоящей из методической погрешности σ_M и погрешности измерения средней скорости

Левую часть уравнения (8) можно трактовать как нормированное значение с.к.о. случайной погрешности измерения скорости

представляющее собой сумму двух составляющих - нормированных значений с.к.о. методической погрешности и с.к.о. погрешности γ_σи средней скорости. Здесь - с.к.о. суммарной погрешности измерения скорости.

Таким образом, выражение (8) может быть представлено в виде:

где γ_σи ²=(σ_x/Δx)²+(σ_t/Δt)².

Исследуем функционал (9) на экстремум с целью определения условий возникновения минимума γ_σΣ на i-м интервале пути Δx_i, то есть минимум выражения

Тогда правая часть уравнения (8) для i-го интервала пути может быть представлена как:

где индексы "i" обозначают i-й интервал пути.

Определим минимум γ_σΣ на i-м интервале пути, приравняв нулю производную по Δх_i от выражения (10):

Преобразуем данное выражение к форме, в которой правая часть будет содержать только погрешности измерения и ускорение на данном интервале пути. Полагая, что расчетный закон движения разгоняемого объекта - равноускоренный [статья: Кириевский Е.В., Михайлов А.А. Выбор расчетного режима для оценки методической погрешности измерителей скорости времяпролетного типа // Известия Сев.-Кавк. научн. центра высш. шк., сер. "Техн. науки", №3-4, 1993, с.92-98] и используя очевидные выражения для i-го интервала пути

2aΔ_i=(V_K+V_H)(V_K-V_H), V_cpi=(V_K+V_H)/2, a_Mi=(V_K-V_H)/2,

имеем

После несложных преобразований из (11) с учетом (12) получаем

Учитывая, что при равноускоренном движении

получаем а=2σ_Mi-1/Δt_i-1.

Подставляя последнее выражение в (13), получаем расчетное выражение для оптимальных значений интервалов пути между соседними точками (координатами) регистрации на контролируемом участке пути:

Выбирая расстояние Δx_i между соседними точками (координатами) регистрации в соответствии с выражением (14), можно обеспечить измерение скорости на i-том интервале пути (начиная со 2-го) с минимальной суммарной погрешностью γ_σ∑.

Анализ выражения (14) показывает, что для определения оптимальных значений интервалов пути Δх_i между соседними точками (координатами) регистрации необходимо знать закон изменения методической погрешности от интервала к интервалу пути и постоянные значения инструментальных погрешностей σ_t и σ_x приборов для измерения времени и интервалов пути соответственно, а в процессе контроля движения объекта измерять время Δt_i-1 прохождения объектом расстояния между соседними точками (координатами) регистрации на предшествующих интервалах пути ΔX_i-1. Закон изменения отношения методических погрешностей согласно [Кириевский Е.В., Михайлов А.А. Исследование методической погрешности измерителей скорости времяпролетного типа // Известия Сев.-Кавк. научн. центра высш. шк., сер. "Техн. науки", №3-4, 1993, с.84-92] определяется из выражения

Тогда, получая из последнего выражения

имеем окончательное выражение для закона измерения отношения методических погрешностей на соседних интервалах, начиная со второго

Следует отметить, что осуществить на первом интервале пути (между первой и второй точками регистрации) требуемую согласно (14) операцию измерения интервала времени прохождения объектом участка траектории, предшествующего участку, на котором измеряется скорость, невозможно в принципе из-за того, что измерения начинаются только с места установки первого датчика. Поэтому необходимо предложить иной механизм определения оптимального интервала пути между первым и вторым датчиками, также обеспечивающий минимизацию суммы методической и инструментальной погрешностей, но не требующий измерения интервала времени прохождения интервала пути, предшествующего первому интервалу пути. Для этого исследуем функционал (9) на экстремум с целью определения условий возникновения минимума γ_σΣ на 1-м интервале пути Δх₁, для которого, как известно [статья: Кириевский Е.В., Михайлов А.А. Исследование методической погрешности измерителей скорости времяпролетного типа // Изв. Сев.-Кавк. науч. центра высш. шк. Техн. науки. 1993. №3-4. С.84-92], характерна максимальная методическая погрешность измерения скорости.

Учитывая, что (как отмечалось выше), в качестве расчетного следует принимать режим равноускоренного движения, а также то, что согласно [там же] с.к.о. методической погрешности на 1-м интервале пути

где Δ_M1mах=aΔt/2 максимальное значение абсолютной методической погрешности на 1-м интервале пути [там же], получаем:

где Δt_i - время движения объекта на 1-м интервале пути.

С учетом (15) правая часть уравнения (8) для 1-го интервала пути имеет вид:

где индексы "1" обозначают 1-й интервал пути.

Определим экстремум описывающей суммарную погрешность функции, взяв производную по Δx_i от выражения (16) и приравняв результат нулю. В результате получаем условие обеспечения минимума суммарной погрешности γ_σΣ на 1-м интервале пути

Учитывая, что для равноускоренного движения V² _cp1=аΔх₁/2, из (17) имеем:

Так как согласно [статья: Кириевский Е.В., Михайлов А.А. Исследование методической погрешности измерителей скорости времяпролетного типа // Изв. Сев.-Кавк. науч. центра высш. шк. Техн. науки. 1993. №3-4. С.84-92]

причем, V_cp1=Δ_M1mах или выражение (18), в свою очередь, может быть представлено как

Таким образом, выбирая расстояние Δx между первой (совпадающей с местом установки первого датчика) и второй точками регистрации в соответствии с выражением (19), можно обеспечить измерение скорости на первом интервале пути Δx₁ с минимальной суммарной погрешностью γ_σ∑.

Как видно из сравнения выражений (14) и (19), для определения оптимального интервала пути между первой и второй точками регистрации в отличие от последующих интервалов не требуется операции измерения интервала времени на предшествующем первому интервалу ("несуществующем") интервале пути.

Анализ, приведенный выше, был проведен для точечного объекта регистрации. При решении задач управляемого разгона реальными объектами, например, в электродинамических ускорителях масс (ЭДУМ), эти объекты имеют обычно протяженные размеры с распределенными по объему параметрами. Естественно уменьшение интервала измерения в способе прототипе приводит к нарушению условия точечности объекта разгона (интервал измерения Δx оказывается соизмеримым с длиной самого объекта), а это приводит к необходимости использовать модель объекта с распределенными параметрами. При этом сохраняется требование необходимости иметь точную информацию о скорости объекта в реальном времени в процессе разгона для формирования команд управления плазменным подводом в ЭДУМ и, особенно, на конечном участке контролируемой траектории движения.

Кроме этого, анализ системы управления [Исследование устойчивости системы стабилизации плазмы с учетом характеристик реальных звеньев / Е.С.Паславский // Управление объектами с распределенными параметрами. - Киев: Институт кибернетики АН УССР. - 1979. - С.55-67] показал, что в ней возможно возникновение колебательного процесса при управлении объектом, даже при обеспечении наиболее простого одномодального описания плазмы. Нестационарность объекта управления приводит к тому, что сила , прикладываемая к объекту в ЭДУМ, случайная функция, распределенная по объему разгоняемого объекта. Следовательно, скорость движения разгоняемого объекта тоже случайная функция и определяется проекцией по направлению движения объекта совокупной (интегрированной по объему) силы. Таким образом, распределенная модель разгоняемого объекта приводит к необходимости усреднения этой функции силы на интервале Т_y, что приводит к выражению (2) и к необходимости определения средней скорости разгоняемого объекта. Причем из этого выражения можно сделать вывод о том, что время усреднения Т_y управляющего воздействия определяет и время осреднения измеряемой величины скорости и если усреднять скорость на интервале времени, меньшем интервала времени Т_y, то процесс детеминированного управления скоростью будет нарушен, что соответствует принципу двойственности измерения и управления, по которому процедуры управления и измерения любого параметра должны осуществляться на одинаковых интервалах усреднения.

Как известно, интервал усреднения измеряемой скорости (во временном диапазоне) определяется неопределенностью регистрации момента появления информационного сигнала. Интервал же усреднения (в координатном измерении) разгоняющей силы определяется интервалом неопределенности в поведении плазмы, который определяется геометрическими параметрами разгоняемого плазменного сгустка. А поскольку измерение скорости производится по одной координате, то интервал усреднения разгоняющей силы не должен быть меньше максимальной длины плазменного сгустка Δx_пл. Из данных рассуждении можно сделать вывод о том, что при измерении скорости движения разгоняемого в рассматриваемой системе объекта существует предельная минимальная величина базового расстояния измерения скорости, на которой возможно пропорциональное управление скоростью движения объекта. В противном случае нарушается уравнение (2) и, следовательно, детерминированное управление невозможно.

Проведенный анализ процедуры измерения показывает, что в процессе измерения необходимо осуществлять контроль прогнозируемой длины интервала измерения скорости и если этот интервал оказывается меньше некоторого заданного интервала

Δх₀=kΔx_пл,

где k - определяется из условия обеспечения качественного измерения скорости, то нарушается принцип двойственности измерения и управление скоростью разгона объекта и следовательно измерение скорости становится бессмысленным, т.е. существует ограничение на диапазон измерения скорости разгона объекта данного класса.

Для исследования возможностей расширения измерения скорости разгона объекта данного класса преобразуем выражение (14) к следующему виду

а для начального участка разгона аналогично выражение (19) к виду

Полученные выражения (20), (21) для σ_t указывают на возможность осуществления управления периодом импульсов эталонной частоты Т_i (T₁ на начальном интервале измерения скорости), которые используются при измерении временного интервала Δt_i. Это обеспечивает дальнейшую минимизацию суммы методической и инструментальной погрешностей измерения скорости, в условиях ограничения на интервал пути между соседними точками регистрации Δx_i. Анализ инструментальных погрешностей измерения временного интервала при методе прямого счета [Орнатский П.П. Автоматические измерения и приборы. Киев. Высшая школа. 1986] показывает, что они определяются, в первую очередь, погрешностью, возникающей при формировании старт-стопных сигналов (δ_к - погрешность формирования стопового сигнала, δ_н - погрешность формирования стартового сигнала) и погрешностью измерения временных интервалов (Δ_к - погрешность измерения конца временного интервала, которая определяется несовпадением импульса эталонной частоты с концом измеряемого интервала времени, Δ_н - погрешность измерения начала временного интервала, которая определяется несовпадением импульса эталонной частоты с началом измеряемого интервала времени). Причем предельная частота дискретизации в методе прямого счета равна максимальной погрешности формирования временного интервала, которая определяется погрешностью формирования старт-стопных сигналов (δ_к+δ_н). Это следует из того, что нецелесообразно производить измерения временного интервала импульсами эталонной частоты, меньшими, чем величина дисперсии его формирования. Предельная же погрешность измерения временных интервалов (Δ_к, Δ_н) также определяется периодом импульсов эталонной частоты.

Таким образом, суть предлагаемого технического решения заключается в том, что, в отличие от способа-прототипа, согласно которому точки регистрации располагают с неравномерным шагом таким образом, что выбор интервалов пути между соседними точками регистрации в соответствии с выражениями (19) на первом интервале пути и (14) на всех последующих интервалах пути, в предлагаемом способе осуществляется также управление периодом эталонной частоты, определяемой по формулам (20) и (21) на начальном интервале измерения скорости, что обеспечивает дальнейшую минимизацию суммы методической и инструментальной погрешностей измерения скорости без нарушения принципа двойственности управления и измерения для детерминированного управления разгоном объекта. В связи с этим заявляемый способ по сравнению со способом-прототипом обеспечивает повышенную точность измерения в более широком диапазоне скоростей.

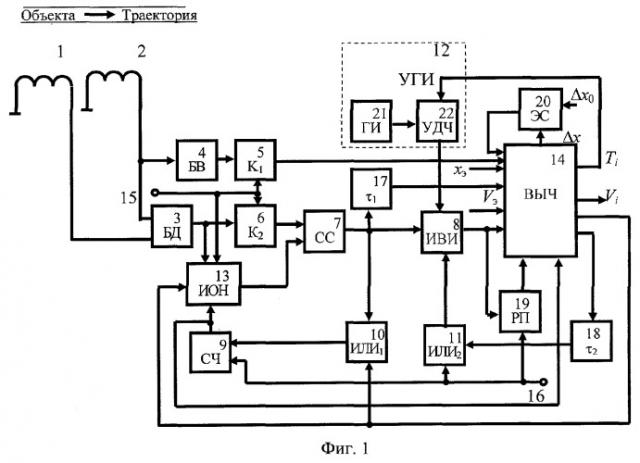
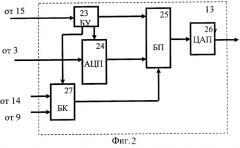
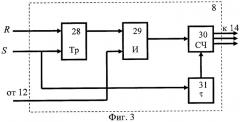
На фиг.1 приведена структурная схема устройства, реализующего способ, на фиг.2 - пример схемной реализация блока памяти 13, на фиг.3 - пример реализации измерителя временных интервалов 8.

Устройство для измерения скорости по данному способу (фиг.1) содержит два датчика положения 1 и 2 (например, индукционных), подключенных к первому и второму входам блока деления (БД) 3. Кроме того, выход второго датчика подключен к блоку выделения (БВ) максимума сигнала 4. Выход БВ 4 соединен с входом управляемого ключа (К₁) 5, выход которого в свою очередь соединен с первым входом вычислителя 14. Второй вход ключа (К₁) 5 объединен с входом управляемого ключа (К₂) 6, выход которого подключен к входу схемы сравнения (СС) 7. Выход СС 7 соединен с измерителем временных интервалов (ИВИ) 8. Кроме того, устройство содержит счетчик импульсов (СЧ) 9, к входу которого подсоединен выход первого элемента "ИЛИ1" 10, вход которого соединен с выходом СС 7. К двум другим входам ИВИ 8 подключены соответственно выход второго элемента "ИЛИ2" 11 и управляемый генератор импульсов (УГИ) 12. К выходу СЧ 9 подключены вход управляемого источника опорного напряжения (ИОН) 13, второй вход вычислителя (ВЫЧ) 14. Выход ИОН 13 подключен к другому входу СС 7. Устройство содержит также шину управления 15, к которой подключены другой вход ИОН 13 и входы ключей 5 и 6. Выход БД 3 соединен с дополнительным входом ИОН 13 и другим входом ключа 6.

Кроме того, устройство содержит шину установки устройства в исходное состояние 16, к которой подключен другой вход СЧ 9 и вход ИЛИ2 11. К третьему входу ВЫЧ 14 подсоединен выход элемента задержки импульсов (τ₁) 17, вход которого соединен с выходом СС7 и входом ИЛИ1 10.

Ко второму входу элемента ИЛИ2 11 подключен выход элемента задержки импульсов (τ₂) 18, к входу которого подключен выход ВЫЧ 14. В устройство входит регистра памяти (РП) 19, первый вход которого соединен с выходом ИВИ В и с четвертым входом вычислителя 14. Второй вход регистра памяти РП 19 соединен с шиной установки устройства в исходное состояние 16, а его выход соединен с пятым входом ВЫЧ 14.

К соответствующим входам ВЫЧ 14 подводятся задаваемые значения x_э и скорости V_э. Первый выход ВЫЧ