Способ и устройство управления ориентируемой ракетой посредством привода, следящего за ориентацией траектории

Способ и устройство управления ориентируемой ракетой посредством привода, следящего за ориентацией траектории

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение касается способа и устройства управления приводимой в движение ракетой, снабженной средствами управления ориентацией, в частности ракетой-носителем с ориентируемыми соплами.

При управлении полетом ракеты-носителя различают наведение и управление. Обобщенно можно сказать, что

- система наведения выдает команды, позволяющие выполнить задачу (заданные значения ориентации). Эти команды позволяют определить движение центра тяжести ракеты-носителя, чтобы она достигла заранее определенной цели (как правило, промежуточная орбита),

- система управления выполняет команды, поступающие от системы наведения, стабилизируя движение ракеты-носителя вокруг ее центра тяжести и учитывая изменения во внешней окружающей среде (возмущения, такие как ветер, порывы ветра и т.д.) и во внутренней среде (разброс и погрешности в параметрах ракеты-носителя и т.д.).

Два предыдущих положения можно уточнить следующим образом.

На основании известных места нахождения цели и текущего положения ракеты-носителя, измеряемого инерционными датчиками, система наведения рассчитывает траекторию, которой должна соответствовать отметка заданного значения ориентации ракеты-носителя (ее начало устанавливают на центре тяжести ракеты-носителя, а одна из ее осей является направлением, которому должна следовать ось ракеты; инерционные измерения ракеты-носителя определяют ориентацию ракеты-носителя, определенную относительно неподвижного ориентира на земле в системе координат, считающейся галилеевой).

Когда на ракету-носитель не действуют никакие возмущения, контур управления откликается мгновенно, ось ракеты совпадает с одной из осей заданной системы координат.

Система управления является контуром автоматического регулирования, первой задачей которого является стабилизация движений ракеты-носителя вокруг ее центра тяжести (понятие устойчивости), как правило, путем регулирования направления реактивной тяги. С другой стороны, система управления по мере возможности реализует заданное значение ориентации, поступающее от системы наведения (система управления является автоматической «исполнительной» системой), и обеспечивает определенный иммунитет ракеты-носителя по отношению к действующим на нее возмущениям (система управления является контуром регулирования). Для этого функциональный блок управления на основании инерциальных измерений ориентации (тех же, что использует система наведения) определяет наиболее приемлемое направление реактивной тяги.

Такое возмущение, как ветер, является помехой для полета ракеты-носителя, создавая движение вокруг ее центра тяжести. В действительности, ветер создает также общее движение ракеты-носителя (поступательное движение или снос). Поскольку система наведения учитывает текущее положение ракеты-носителя (при помощи инерционных измерений) для выработки новой траектории вплоть до конечной точки, то не будет ошибкой рассматривать только движения вокруг центра тяжести для выработки данных, предназначенных для эффективной работы функционального блока управления.

Функция управления должна учитывать некоторые особенности, в частности то, что по своей сути ракета-носитель не является стационарной системой. Ее физические характеристики (положение центра тяжести, масса, инерция) и аэродинамические характеристики изменяются в зависимости от полета. С функцией управления взаимосвязаны переходные фазы, среди которых такие, как отделение ступени, наличие внешних возмущений (ветер) и внутренних возмущений (например, смещение направления реактивной тяги). Наконец, как и в любой физической системе, на параметры ракеты-носителя влияют погрешности.

Функцию управления устанавливают на основании полетного задания строго с учетом указанных выше элементов. Обычно это полетное задание включает в себя:

стабилизацию ракеты-носителя;

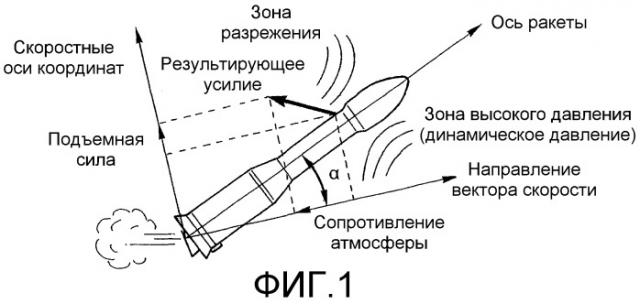
выравнивание ракеты-носителя и минимизацию угла атаки α в фазе полета в слоях атмосферы (фиг.1);

следование заданному значению ориентации, вырабатываемому системой наведения;

устранение последствий внешних и внутренних возмущений;

учет характеристик серворуля.

Как правило, алгоритм управления вводится в виде рекуррентных уравнений (повторно) в цифровую вычислительную машину. На основании информации, поступающей от датчиков (ориентация, скорость ориентации, ускорения) и навигационных приборов, алгоритм наведения рассчитывает заданные значения ориентации, которые реализует контур управления и которые, таким образом, используются в алгоритме управления.

Обычно правила управления формируют на основании предположения о возможности разъединения осей тангажа (горизонтальная ось), рысканья (вертикальная ось) и крена (продольная ось). Это предположение позволяет синтезировать (сформулировать) правило с использованием одноосной модели, действительной для малых углов. Эффект объединения трех правил (по одному для каждой оси) впоследствии проверяется трехосным моделированием.

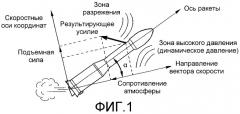
На фиг.2 показана одноосная функциональная схема управления. Алгоритм управления рассматривается как «черный ящик», содержащий информацию, поступающую от датчиков ракеты-носителя (инерционный блок для измерения ориентации и гирометр для измерения скорости ориентации), и определяющий команду для одноосного привода, в данном случае сопла.

Одноосная схема предполагает, что движение ракеты-носителя является движением в плоскости. С другой стороны, положение привода регулируется автоматически. Он принимает положение, соответствующее заданному значению регулирования сопла, выражающегося в удлинении.

Предшествующий уровень техники

Основной трудностью, с которой сталкивается разработчик системы управления, является использование физических условий, которым должно удовлетворять правило управления для определения математического критерия, который затем может быть оптимизирован. Для такого использования необходимо отойти от физической сущности условий, чтобы найти адекватное математическое выражение.

Например, устойчивость (с физической точки зрения) выражается в качестве затухания временного отклика контура управления, на который действует возмущение или подается команда. С математической точки зрения можно также сказать, что степень устойчивости (качество затухания) связана с коэффициентом перенапряжения контура управления (резонанс контура управления на данной частоте). Четкая связь между затуханием и коэффициентом перенапряжения существует только, в так называемых, академических системах (системах второго порядка).

Несмотря на эти ограничения, в современных разработках правил управления используют скорее понятие перенапряжения, чем понятие затухания, чтобы учитывать проблему устойчивости, так как это понятие перенапряжения наиболее соответствует критериям, выработанным на основании минимизации математической нормы. Поскольку связь между перенапряжением и затуханием не является прямой, то затухание определяют только впоследствии путем моделирования по времени.

В известных правилах управления используют следующие алгоритмы синтеза:

метод LQG (А4, М45, А5);

метод Н∞ (А5).

В каждом алгоритме используются параметры синтеза, позволяющие оптимизировать правило, чтобы оно отвечало требованиям и условиям, необходимым для управления (устойчивость, эффективность выравнивания, надежность устойчивости и работы).

Указанные методы синтеза предназначены для обобщения различных задач с использованием понятия стандартной системы. Большинство задач анализа, а также синтеза управления могут быть записаны в виде одной и той же стандартной схемы, с помощью которой можно формулировать условия в виде математического критерия, который стремится минимизировать (норма Н₂ или Н∞). Таким образом, понятие стандартной проблемы имеет огромное значение для обобщения задач в виде единого математического критерия. Однако такое обобщение происходит за счет отхода от физического смысла, который будет иметь результирующий критерий.

С другой стороны, приведение к стандартной форме, как правило, приводит к усложнению алгоритма. Поскольку параметры стандарта не обязательно подходят для решения поставленной проблемы, то приходится допускать дополнительные степени свободы (откуда происходит увеличение порядка) для правильного ретранскрибирования поставленных задач.

Используемые в настоящее время новейшие методы вносят неоспоримый вклад в анализ и синтез задач управления. С другой стороны, получаемый в результате критерий, на основании которого осуществляют синтез задач управления, приводит к применению метода «проб и ошибок» для нахождения удовлетворительного результата.

Решения, полученные с помощью этих алгоритмов, не позволяют добиться взаимосвязи между поведением по частоте и поведением во времени иначе, как путем моделирования, в частности, высокого уровня перенапряжения замкнутого контура, коррелированного с удовлетворительным затуханием. Таким образом, оптимальное правило можно получить только путем последовательных итераций «синтез-моделирование-проверка».

Краткое изложение сущности изобретения

Технической задачей настоящего изобретения является создание способа и устройства ориентируемой ракетой посредством следящего привода по отношению к траектории, подверженной воздействию внешних возмущений, в которых используют алгоритм управления, параметры которого могут коррелироваться с физическими условиями, задаваемыми для управления.

Поставленная задача решена путем создания способа управления ориентируемой ракетой посредством привода, следящего за ориентацией траектории, подверженной воздействию внешних возмущений, указанный способ заключается в том, что по меньшей мере для тангажа (горизонтальная ось)

предварительно определяют правило управления, содержащее поправочный член первого порядка, переходный член, содержащий характеристические параметры ракеты и внешних возмущений, коэффициент усиления ориентации и коэффициент усиления скорости ориентации,

предварительно определяют коррелирующие связи между коэффициентом усиления скорости ориентации и параметрами поправочного члена в зависимости от коэффициента усиления ориентации, параметров переходного члена ракеты и двух членов, представляющих собой заданные значения быстроты и затухания контура управления,

по меньшей мере для одной фазы полета определяют значения параметров переходного члена ракеты и выбирают коэффициент усиления ориентации и члены быстроты и затухания, из которых выводят параметры поправочного члена и коэффициент усиления скорости, и для привода используют правило управления с этими значениями параметров.

Согласно изобретению предложено также устройство управления, предназначенное для реализации описанного выше способа, содержащее вход, для приема по меньшей мере одного измерения ориентации тангажа, выход, предназначенный для передачи команды на привод, по меньшей мере один контур автоматического регулирования тангажа, подключенный между входом и выходом и содержащий корректировочный фильтр первого порядка, при этом переходный член содержит характеристические параметры ракеты и внешних возмущений, коэффициент усиления ориентации и коэффициент усиления скорости ориентации.

Можно отметить, что столь простой выбор правила управления идет вразрез с современным анализом, используемым специалистами в данной области техники, согласно которому простой алгоритм, то есть содержащий небольшое число параметров, мало подходит для нормального управления. Тем не менее, вопреки ожиданиям, столь простой выбор правила управления позволить сформулировать правила, позволяющие, с некоторым упрощением, например, путем ограниченного развертывания замкнутого контура, коррелировать параметры правила с физическими параметрами, такими как затухание (значит, устойчивость) и быстрота автоматического регулирования (значит, эффективность во времени), коэффициентом усиления ориентации вокруг рассматриваемой оси, а также с физическими параметрами моделирования.

Краткое описание чертежей

В дальнейшем отличительные признаки и преимущества настоящего изобретения поясняются описанием предпочтительного варианта воплощения со ссылками на сопровождающие чертежи, на которых:

фиг.1 изображает классическую схему воздействий на ракету, на которую действует динамическое давление;

фиг.2 - известную схему одноосной системы управления;

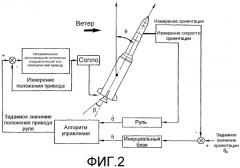
фиг.3 - известную схему, определяющую различные углы для данных осей;

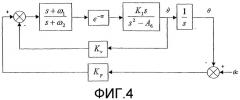
фиг.4 - схему архитектуры аналитического правила управления, используемого для данной оси согласно изобретению;

фиг.5 - вариант схемы архитектуры для случая, когда угловая скорость вокруг рассматриваемой оси не измерена, согласно изобретению;

фиг.6 - кривую, коррелирующую коэффициент усиления и фазу разомкнутого контура в номинальном случае и в так называемых случаях НЧ и ВЧ, согласно изобретению;

фиг.7 и 8 - кривые, показывающие реагирование ракеты по ориентации, регулированию сопла и угла атаки замкнутого контура управления для НЧ (А6_min, K1_max) и ВЧ (A6_max, K1_min), согласно изобретению.

Подробное описание предпочтительных вариантов воплощения изобретения

В соответствии с настоящим изобретением используют необходимый (в смысле сложности) алгоритм управления для обеспечения управления ракетой.

Алгоритм основан на родовой структуре, параметры которой рассчитывают строго в зависимости от параметров соответствующей ракеты и требуемых характеристик управления (отслеживание траектории, минимизация угла атаки, промежуточные фазы и т.д.). Правило четко учитывает погрешности параметров ракеты и запаздывание глобализованной цепи (запаздывание, обусловленное динамикой привода + запаздывание датчиков + запаздывание по причине дискретизации).

Это правило применимо для нестационарных систем (изменение параметров ракеты-носителя). Нестационарное правило получают быстро, так как его параметры являются формальными. В силу родовой структуры не возникает проблем, связанных с интерполяционными приемами, широко используемыми в системах управления ракетами-носителями.

Неоспоримым преимуществом этого метода является то, что параметры синтеза являются физическими параметрами высшего уровня (затухание замкнутого контура, полоса пропускания). Известно приведение к этим параметрам соответствующей физической величины и соответствующей задачи. Таким образом, регулирование осуществляют непосредственно на основании физических условий, устанавливаемых разработчиком.

Это вытекает из нижеследующих пояснений, которые для большей простоты ограничиваются управлением жестким режимом полета ракеты. Возможное присутствие гибких режимов может быть учтено при выборе «осторожной политики», то есть избегая возбуждения гибких режимов при помощи контурного усиления правила управления (например, путем добавления фильтра-аттенюатора).

Разработка правила управления требует использования модели ракеты-носителя, называемой моделью синтеза. Некорректируемая динамика разомкнутого контура может быть представлена двумя объединенными уравнениями, описывающими движения при ориентации и сносе ракеты-носителя (фиг.3).

Разработка правила управления требует выбора соответствующей модели ракеты-носителя, называемой моделью синтеза.

Некорректируемая динамика разомкнутого контура может быть представлена, со ссылками на величины, определенные на фиг.3, в виде двух объединенных уравнений, описывающих движения ориентации и сноса ракеты.

Прежде всего, если ограничиться малыми углами, момент для тангажа может быть определен уравнениями (1), приведенными в Приложении, тогда как силы, действующие поперечно относительно оси скорости воздуха, могут быть определены при помощи уравнений (2).

Кроме того, различные углы (фиг.3) связаны уравнением (3), которое после дифференцирования по времени дает уравнение (4).

После исключения γ в уравнениях (2) и (4) получают систему уравнений (5), где s является переменной Лапласа.

Если предположить, что члены, идентифицированные в условии (С), являются малыми для значений, содержащихся в полосе пропускания контура управления, то к выражению (5) можно прийти через выражение (6).

Это выражение показывает, что система является системой второго порядка с динамикой первого порядка, неустойчивой при пульсации

Система уравнений (6) представляет собой модель синтеза, на основании которой будут выработаны основы аналитического синтеза.

Отсюда вытекает, что переход команды, то есть переход между контролируемой переменной (θ) и командой (регулирование сопла β) выражается членом K₁/(s²-A₆).

Поведение серворуля и измерительной цепи может быть смоделировано при помощи общего чистого запаздывания τ цепи последовательно с переходом команды, откуда получают выражение (7), где G' с точки зрения автоматики является математическим выражением физической системы, которую необходимо облечь в контур.

Чистое запаздывание в упомянутом выражении получено путем аппроксимации PADE первого порядка.

Включение в контур осуществляют таким образом, чтобы соответствующий замкнутый контур отвечал требованиям устойчивости и эффективности.

Примеры родовых архитектур аналитического правила управления

На фиг.4 показана родовая архитектура аналитического правила управления. Она представлена с предположением того, что измерения ориентации, а также скорости ориентации являются доступными, но, как будет показано ниже, это предположение не является ограничением метода.

В этой архитектуре запаздывание τ объединяет запаздывание цепи, запаздывание в результате дискретизации-блокировки, а также запаздывание, эквивалентное фазовому отставанию руля. Это запаздывание может также включать в себя отставание по фазе фильтра, предназначенного для локальной аттенюации контурного усиления правила управления, чтобы обеспечить надежность усиления в гибком режиме ракеты-носителя.

В прямую цепь вводят поправочный член первого порядка и коэффициент усиления скорости ориентации (К_v) и коэффициент усиления ориентации (К_р). В этом случае порядок правила управления равен 1.

Производят оценку первой динамики способа в замкнутом контуре для его фиксирования на модели второго порядка параметров (ζ, ω_n). Этот прием позволяет аккуратно сконденсировать компромисс эффективность-устойчивость. Затухание обеспечивает определенную степень устойчивости, тогда как ω_n (быстрота автоматического регулирования) порождает эффективность во времени. Таким образом, параметры (ζ, ω_n) представляют собой регулировочные параметры «высшего уровня».

После этого осуществляют ограниченное развертывание замкнутого контура до третьего порядка. Получают систему трех уравнений, на основании которых выводят три из четырех регулировочных параметров правила управления (К, ω₁, ω₂) в зависимости от (К_р, ω_n, ζ) при помощи уравнений (8).

Чтобы не загромождать изложение, предыдущие решения были сформулированы без учета общего запаздывания контура τ. При его наличии эти решения становятся гораздо более сложными. Тем не менее, решения всегда есть и могут быть легко интегрированы в компьютерную программу синтеза правила. При этом можно сформулировать следующие замечания:

полюс поправочного члена прямой цепи является нестабильным (ω₂<0);

параметры (К_v, ω₁, ω₂) являются функцией К_р. С точки зрения математики можно было бы определить К_р и два других параметра в зависимости от четвертого. Однако будет более правильным оставить К_р в качестве свободного параметра, так как его можно выбирать независимо от динамики замкнутого контура. Нулевое значение К_р способствует минимизации угла атаки ракеты, тогда как не нулевое значение приведет к отслеживанию и регулированию ориентации ракеты-носителя;

ноль поправочного члена компенсирует устойчивую динамику ракеты (ω₁=);

при А₆=0 полюс и ноль поправочного члена прямой цепи стремятся к 0. Устойчивость системы обеспечивается опережением фазы, хорошо известным в классических способах управления и определяемым как К_р+sK_v.

Определение параметров правила показывает, что они были рассчитаны на основании параметров высшего уровня (затухание и быстрота замкнутого контура). Это позволяет установить связь между затуханием и запасом устойчивости автоматического регулирования, выраженным в виде предела усиления М₀ (напомним, что предел усиления является значением коэффициента усиления разомкнутого контура, когда его вход и выход смещены по фазе на 180°, при этом правильную нестабильность получают при значении предела усиления=1), получаемого при помощи уравнения (9).

Заметим, что доводку предела усиления осуществляют по ζ (затухание замкнутого контура). В частности, он является минимальным при нулевом коэффициенте усиления ориентации (К_р=0). Его значение получают из уравнения (10).

Если выбирают динамику замкнутого контура, определяемую как ω_n= (в этом случае ракета-носитель стабилизирована), то предел усиления определяется выражением (11).

Это выражение устанавливает прямую связь между затуханием и запасом устойчивости.

Вышеуказанный метод можно применять, даже если измерение скорости ориентации недоступно. В этом случае ее оценивают при помощи чистого (наличие члена прямой передачи на высоких частотах) или строго чистого (ограничение коэффициента усиления фильтра на высоких частотах с крутизной, по меньшей мере, равной 20 дБ на декаду) фильтра высоких частот. Выберем фильтр высоких частот с ограничением в 20 дБ на декаду. Его выражение определяется уравнением (12).

В этом случае правило управления становится моноконтурным правилом, архитектура которого показана на фиг.5.

Как и в случае с обратным сигналом скорости ориентации, выражения правила управления (ω₁, ω₂, К_v) могут быть полностью определены путем развертывания замкнутого контура до третьего порядка и в зависимости от параметров К_р, ω_n, ζ, ω_c и τ.

Выбор параметров регулирования

Отслеживание ориентации обязательно приводит к измерению угла атаки, которое может быть затруднено с точки зрения общих усилий, действующих на ракету-носитель. Поэтому выбор коэффициента усиления ориентации осуществляют следующим образом.

Необходимо установить ненулевое значение К_р, если требуется обеспечить хорошее отслеживание ориентации (старт, фаза полета за пределами атмосферы).

Низкое или нулевое значение К_р необходимо выбирать для минимизации угла атаки в критических фазах полета, соответствующих максимальному динамическому давлению.

Значение ω_n определяет быстроту ответной реакции контура управления. Пульсацию ω_n следует выбирать таким образом, чтобы выравнивание ракеты-носителя при максимальном динамическом давлении было совместимым с допустимым углом атаки и характеристиками серворуля. Таким образом, регулировочный параметр ω_n тесно связан с задачей эффективности правила управления. При выборе ω_n необходимо учитывать погрешности в параметрах ракеты-носителя (задача надежности при эффективности).

Устойчивость и надежность устойчивости устанавливаются параметром ζ таким образом, чтобы все ракеты-носители, характеризующиеся вариациями параметров А₆ и К₁ были стабилизированы при затухании, по меньшей мере, равном затуханию, заданному разработчиком.

Нестационарное развитие правила

Учитывая различные условия, возникающие во время полета (старт, отслеживание траектории, устойчивость ракеты в критических фазах, точность вывода на орбиту (гражданская ракета-носитель) или точность стрельбы (военная ракета)), наиболее приемлемое правило вытекает из интерполяции нескольких линейных правил, рассчитываемых в различные моменты полета. В данном случае параметры правила становятся функциями времени. Поскольку структура поправочного члена является родовой, интерполяцию этих параметров можно осуществить напрямую, при этом они сохраняют одну и ту же физическую сущность от одного момента к другому.

В момент t полета определяют:

параметры ракеты-носителя A₆(t) K₁(t);

коэффициент усиления ориентации Kp(t);

быстроту контура управления ω_n(t);

затухание ζ(t), которое можно выбирать постоянным для всего полета.

Параметры правила, соответствующие моменту t, оцениваются на основании формул, получаемых при ограниченном развертывании замкнутого контура.

Процесс синтеза возобновляется для n точек полета рассматриваемой ступени. Общее нестационарное правило получают путем интерполяции n стационарных правил.

Расширение структуры правила

Аналитическое правило имеет две родовые базовые формы в зависимости от наличия или отсутствия обратного сигнала скорости ориентации, которые получают при помощи уравнений (13) и (14).

Эти формы могут быть расширены, хотя сущность решения определяется одной из двух базовых форм. Первое предложение состоит в усложнении одной или другой базовой формы путем их умножения при помощи фильтра любого порядка. Этот фильтр предназначен либо для локального ограничения коэффициента усиления по частотам, чтобы избежать возбуждения гибких режимов ракеты-носителя на отдельных частотах, либо для аттенюации коэффициента усиления контура, начиная с какой-либо частоты, определяемой разработчиком.

Само собой разумеется, что можно использовать другой тип фильтра, который не выполняет никакой другой специальной функции, кроме видимого усложнения одной из двух базовых форм.

Физическая сущность и типовые значения параметров

С учетом аналитического выражения параметров К_v, ω₁ и etω₂ некоторым из них можно придавать данный физический смысл.

Пульсация ω₁ равна в силу динамики самой ракеты-носителя. Осуществляют ее компенсацию. В частности, можно записать, что пульсация ω₁ пропорциональна динамическому давлению в рассматриваемый момент полета и обратно пропорциональна инерции ракеты-носителя. Ее значение изначально трудно определить количественно, так как оно зависит от характеристик ракеты-носителя.

Выражение пульсации ω₂ является функцией быстроты, выбранной для контура управления. Так же, как и в предыдущем случае, можно уточнить, что чем больше будет значение ω₂, тем быстрее будет работать контур управления. На практике быстроту контура выбирают такой, чтобы он не заставлял средство (ракета-носитель) выходить за пределы собственной динамики ().

Выражение коэффициента усиления К_v является относительно сложным. Кроме членов К₁, А₆, К_р и ω_n появляется член затухания ζ, являющийся параметром, устанавливающим устойчивость и надежность устойчивости контура управления. С точки зрения качества степень устойчивости автоматического регулирования тем выше, чем больше числовое значение K_v, которое пропорционально ζ.

Пример

Приведенный ниже пример показывает применение аналитического синтеза стационарного правила управления для ракеты-носителя Х. Значения параметров А6 и К1 при максимальном динамическом давлении (соответствующем фиксированной траектории) получают из:

А6=35±15 с^-2

К1=30±10 с^-2

Мажоранта для устойчивости ракеты-носителя соответствует:

А6=А6max=50 с^-2

K1=K1min=20 с^-2

Правило управления синтезируют при максимальном динамическом давлении с вышеуказанными параметрами ракеты-носителя. Затухание динамики замкнутого контура устанавливают:

ζ=0,3 (это требуемое затухание, соответствующее мажоранте)

С целью минимизации угла атаки при максимальном динамическом давлении устанавливают нулевой коэффициент усиления положения, то есть:

Кр=0

Выбор параметра ω_n (устанавливающего быстроту автоматического регулирования) определяют, проверяя, чтобы его значение позволяло не превышать скорость и отклонение поворота, которых может достичь руль. Предполагают, что значение ω_n известно и равно:

ω_n=3,5 рад/с

Если это не соответствует предположению, то этап синтеза поправочного члена повторяют до тех пор, пока не найдут значение ω_n, совместимое с характеристиками руля, проверенными при помощи моделирования по времени.

Параметры поправочного члена получают при помощи уравнений, лежащих в основе изобретения. Мы имеем (для Кр=0)

Применение формул предполагает, что цепь управления не вносит запаздывания. Если такое предположение не проверено, то необходимо заново оценить аналитические выражения параметров поправочного члена с учетом наличия запаздывания цепи.

Предел усиления на низкой частоте получают из аналитического выражения

то есть 2 дБ при

Моделирование по времени показывает, что получают максимальный поворот сопла в 5,6° и максимальную скорость поворота сопла в 30°. Эти цифры получены для мажоранты с точки зрения устойчивости (случай A6max, K1min, называемый случаем НЧ).

Частотные характеристики показаны на фиг.6. В частности, при помощи моделирования опять находят предел усиления, рассчитанный в случае мажоранты (A6max, K1min).

Временные характеристики, полученные путем расчетного регулирования, показаны в виде кривых на фиг.7 и 8.

Аналитическое правило управления позволяет быстро выполнить задачи устойчивости и эффективности для совокупности ракет-носителей, описанные при помощи вариаций параметров А6 и К1. В отличие от методов типа LQG или H∞ можно отказаться от частотной итерации, состоящей в последующей проверке запасов устойчивости. Временная итерация, позволяющая выбрать быстроту контура управления, по-прежнему необходима, так как задача эффективности напрямую связана с природой возмущений, действующих на ракету-носитель (ветер, порывы, внутренние возмущения и т.д.). Нестационарное расширение является прямым и не вызывает особых проблем с точки зрения синтеза.

В случае необходимости аналитическое правило управления можно распространить на другие аппараты, кроме ракет-носителей. При принципиальном рассмотрении можно отметить, что его вырабатывают на основании модели синтеза, выведенной из уравнений механики полета, при этом наиболее существенным предположением является неустойчивость летательного аппарата. Поэтому нет никакого ограничения для того, чтобы этот тип правила мог быть применен для самолетов, не устойчивых на одной или нескольких осях полета (тангаж, рысканье и крен). Для этого достаточно применить уравнения механики полета для неустойчивых самолетов. Это позволит получить новую модель синтеза, из которой можно вывести параметры аналитического правила управления.

Предпочтительно:

для фазы полета определяют значения (A6max, K1min) параметров переходного члена, мажорирующие внешние возмущения;

применяют тест принятия моделированием для выбора коэффициента усиления ориентации и членов быстроты и затухания для всего времени полета и эти выбранные параметры применяют в течение всего полета, если они прошли проверку на достоверность, а если нет, то время полета разбивают на несколько фаз;

переходный член определяют для внешних возмущений, в основном возникающих от действия атмосферного воздуха;

по продольной оси и по вертикальной оси применяют правила управления, определенные тем же методом, что и правило управления по горизонтальной оси.

ПРИЛОЖЕНИЕ: ФОРМУЛЫ

где

m: масса ракеты-носителя;

Q: динамическое давление;

C_zα: градиент подъемной силы;

I: инерция по горизонтальной оси;

S: ссылочная поверхность аппарата для подъемной силы;

Pc: реактивная тяга аппарата;

Lf: расстояние (центр тяжести - аэродинамический фокус);

Lt: расстояние (центр тяжести - центр вращения сопла).

где

(Скорость Vz является проекцией скорости ракеты-носителя на вертикальную ось)

1. Способ управления ориентируемой ракетой посредством привода, следящего за ориентацией траектории, подверженной воздействию внешних возмущений, заключающийся в том, что по меньшей мере для тангажа (для горизонтальной оси) предварительно определяют правило управления, содержащее поправочный член первого порядка, переходный член, содержащий характеристические параметры ракеты и внешних возмущений (А₆, К₁), коэффициент (К_р) усиления ориентации и коэффициент (К_v) усиления скорости ориентации, предварительно определяют коррелирующие связи между коэффициентом усиления скорости ориентации и параметрами поправочного члена в зависимости от коэффициента усиления ориентации, параметров переходного члена ракеты и двух членов, представляющих собой заданные значения быстроты (ω_n) и затухания (ζ), по меньшей мере для одной фазы полета ракеты определяют значения параметров переходного члена и выбирают коэффициент усиления ориентации и члены быстроты и затухания, по которым выводят параметры поправочного члена и коэффициента усиления скорости, и для привода применяют правило управления с этими значениями параметров.

2. Способ по п.1, отличающийся тем, что корреляционные правила определяют на основании ограниченного развертывания уравнения замкнутого контура, образованного ракетой и ее приводом.

3. Способ по п.1, отличающийся тем, что для фазы полета определяют значения (А_6mах, K_1min) параметров переходного члена, которые мажорируют внешние возмущения.

4. Способ по п.1, отличающийся тем, что для правила управления дополнительно предусматривают использование фильтра.

5. Способ по любому из пп.1-4, отличающийся тем, что правило управления применяют с использованием измерений ориентации и скорости ориентации.

6. Способ по любому из пп.1-4, отличающийся тем, что правило управления применяют с использованием оценочного фильтра, предназначенного для оценки скорости ориентации в правиле управления.

7. Способ по любому из пп.1-4, отличающийся тем, что применяют тест валидации моделированием для выбора коэффициента усиления ориентации и членов быстроты и затухания в течение всего времени полета и эти выбранные параметры используют в течение всего полета, если выбранные параметры прошли валидацию, а если нет, то время полета разбивают на несколько ф