Устройство и способ для обработки, по меньшей мере, двух входных значений

Устройство и способ для обработки, по меньшей мере, двух входных значений

Иллюстрации

Показать все

Реферат

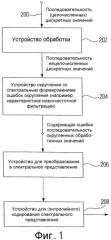
Предложенное изобретение относится к обработке сигналов, более конкретно к обработке сигналов для последовательно поступающих значений, например значений выборок аудиоданных или значений выборок видеоданных, которые, в частности, пригодны для приложений кодирования без потерь.

Предложенное изобретение также подходит для алгоритмов сжатия для дискретных значений, которые имеют аудио- и/или видеоинформацию, в частности для алгоритмов кодирования, которые включают в себя преобразование в частотную область, или временную область, или область местоположения, за которыми следует кодирование, например энтропийное кодирование в форме кодирования Хафмана или арифметического кодирования.

Современные способы аудиокодирования, например, MPEG уровня 3 (MP3) или MPEG AAC применяют преобразования, например так называемое модифицированное дискретное косинусное преобразование (МДКП), чтобы получать блочное частотное представление аудиосигнала. Подобный аудиокодер получает обычно поток дискретных по времени значений выборок аудиосигнала. Поток значений выборок аудиосигнала подвергается взвешиванию функцией окна, чтобы получать взвешенный блок, например, 1024 или 2048 значений выборок аудиосигнала. Для взвешивания функцией окна используются различные функции окна, например синусоидальное окно и т.д.

Взвешенные функцией окна дискретные по времени значения выборок аудиоданных затем преобразуются посредством набора фильтров в спектральное представление. В принципе, для этого может использоваться преобразование Фурье или, из-за особых причин, некоторый производный тип преобразования Фурье, например быстрое преобразование Фурье (БПФ) или МДКП. Блок спектральных значений аудиоданных на выходе набора фильтров может, по мере необходимости, подвергаться дальнейшей обработке. В случае вышеописанных аудиокодеров осуществляется так называемое квантование спектральных значений аудиоданных, причем шаг квантования выбирается таким образом, чтобы шумы квантования, обусловленные квантованием, находились ниже психоакустического порога маскирования, то есть были замаскированными. Квантование представляет собой кодирование с потерями. Чтобы получить дальнейшее сокращение объема данных, квантованные спектральные значения затем кодируются, например, путем энтропийного кодирования Хафмана. За счет добавления вспомогательной информации, например масштабирующих коэффициентов и т.д., из энтропийно кодированных квантованных спектральных значений посредством мультиплексора битового потока формируется битовый поток, который сохраняется или передается.

В аудиодекодере битовый поток посредством демультиплексора битового потока разделяется на кодированные квантованные спектральные значения и вспомогательную информацию. Энтропийно кодированные квантованные спектральные значения сначала подвергаются энтропийному декодированию, чтобы получить квантованные спектральные значения. Квантованные спектральные значения затем подвергаются обратному квантованию, чтобы получить декодированные спектральные значения, содержащие шумы квантования, которые лежат ниже психоакустического порога маскирования и поэтому становятся неслышимыми. Эти спектральные значения затем преобразуются посредством набора фильтров синтеза во временное представление, чтобы получить дискретные по времени декодированные значения выборок аудиосигнала. В наборе фильтров синтеза должен применяться алгоритм преобразования, обратный вышеупомянутому алгоритму преобразования. Кроме того, после обратного частотно-временного преобразования взвешивание функцией окна должно осуществляться в обратном направлении.

Для того чтобы достичь хорошей избирательности по частоте, современные аудиокодеры в типовом случае применяют перекрытие блоков, как показано на фиг.6а. Сначала, например, берутся 2048 дискретных по времени значений выборок аудиосигнала и подвергаются взвешиванию функцией окна посредством устройства 402. Окно, реализуемое устройством 402, имеет длину окна, равную 2N значений выборок, и выдает на выход блок из 2N значений выборок. Чтобы получить перекрытие окон, сначала посредством устройства 404, которое на фиг.6а показано отдельно от устройства 402 только для наглядности, формируется второй блок из 2N взвешенных функцией окна значений выборок. Однако введенные в устройство 404 2048 значений выборок не являются дискретными по времени значениями выборок аудиосигнала, непосредственно примыкающими к первому окну, а содержат вторую половину значений выборок, взвешенных функцией окна с помощью устройства 402, и дополнительно только 1024 "новых" значений выборок. Перекрытие символически представлено на фиг.6а с помощью устройства 406, которое обеспечивает степень перекрытия 50%. Как 2N взвешенных значений выборок, выданных устройством 402, так и 2N взвешенных значений выборок, выданных устройством 404, затем подвергаются обработке в соответствии с алгоритмом МДКП посредством устройства 408 или 410. Устройство 408 выдает, согласно известному алгоритму МДКП, N спектральных значений для первого окна, в то время как устройство 410 выдает также N спектральных значений, но для второго окна, причем между первым окном и вторым окном имеется перекрытие 50%.

В декодере N спектральных значений первого окна, как показано на фиг.6b, подаются на устройство 412, которое выполняет обратное модифицированное дискретное косинусное преобразование. То же самое справедливо для N спектральных значений второго окна. Они подаются на устройство 414, которое также выполняет обратное модифицированное дискретное косинусное преобразование. Как устройство 412, так и устройство 414 выдают соответственно 2N значений выборок для первого окна и 2N значений выборок для второго окна.

В устройстве 416, как обозначено на фиг.6b аббревиатурой TDAC (компенсация наложения спектров во временной области), учитывается тот факт, что оба окна перекрываются. В частности, значение выборки y₁ второй половины первого окна, то есть с индексом N+k, суммируется с значением выборки y₂ первой половины второго окна, то есть с индексом k, так что на выходе, то есть в декодере, получается N декодированных временных значений выборок.

Следует отметить, что за счет функции устройства 416, которая также называется функцией суммирования, взвешивание функцией окна, проводимое в схематично представленном на фиг.6а кодере, в известной степени учитывается автоматически, так что в декодере, представленном на фиг.6b, в явном виде не производится никакого "инверсного взвешивания функцией окна".

Если обозначить функцию окна, реализуемую устройством 402 или 404 как w(k), где индекс k представляет собой временной индекс, то должно выполняться условие, что вес окна w(k) в квадрате, суммированный с весом окна w(N+k) в квадрате, дает 1, причем k изменяется в пределах от 0 до N-1. Если применяется синусное окно, вес которого соответствует первой полуволне функции синуса, то это условие всегда выполняется, так как квадрат синуса и квадрат косинуса для каждого угла в сумме дают 1.

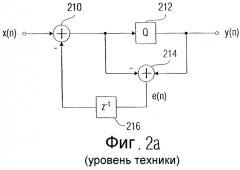
Недостаток способа взвешивания функцией окна, описанного со ссылкой на фиг.6а, с последующим применением функции МДКП заключается в том обстоятельстве, что взвешивание функцией окна реализуется посредством умножения дискретных по времени значений выборок, в предположении синусного окна, с использованием числа с плавающей запятой, так как синус угла в пределах от 0 до 180 градусов, исключая угол 90 градусов, не дает целого числа. И в случае, когда взвешиванию функцией окна подвергаются целочисленные значения выборок, после взвешивания функцией окна возникают также числа с плавающей запятой.

Поэтому, и без применения психоакустического кодера, то есть, когда должно быть реализовано кодирование без потерь, на выходе устройств 408 или 410 необходимо квантование, чтобы иметь возможность проведения до некоторой степени обозримого энтропийного кодирования.

Таким образом, современные известные целочисленные преобразования для аудио- и/или видеокодирования без потерь реализуют за счет разложения применяемых при этом преобразований на Givens-вращения и применения схем поднятия для каждого Givens-вращения. Тем самым на каждом шаге вводится ошибка округления. Для последующих ступеней Givens-вращений ошибка округления все больше аккумулируется. Получающаяся в результате ошибка аппроксимации становится, особенно для аудиокодирования без потерь, проблематичной, в частности, если применяются длинные преобразования, которые вырабатывают, например, 1024 спектральных значения, как это имеет место, например, для известного МДКП с перекрытием и суммированием. В частности, в высокочастотной области, где аудиосигнал и без того имеет в типовом случае очень малое содержание энергии, ошибка аппроксимации может быстро становиться большей по величине, чем действительный сигнал, так что такие применения в отношении кодирования без потерь и, в частности, в отношении достижимой эффективности кодирования являются проблематичными.

Целочисленные преобразования, то есть алгоритмы преобразования, которые вырабатывают целочисленные выходные значения, основываются, в аспекте аудиокодирования, в частности, на известном ДКП-IV, которое не учитывает постоянную составляющую, в то время как целочисленные преобразования применительно к изображениям скорее базируются на ДКП-II, которое содержит режимы, специально предусмотренные для постоянной составляющей. Такие целочисленные преобразования известны, например, из следующих работ: Y.Zeng, G.Bi, Z.Lin, "Integer sinusoidal transforms based on lifting factorization", Proc. ICASSP'01, May 2001, p.1.181-1.184; K.Komatsu, K.Sezaki, "Reversible Discrete Cosine Trasnsform", Proc. ICASSP, 1998, V.3, p.1.769-1.772; P.Hao, Q.Shi, "Matrix factorizations for reversible integer mapping", IEEE Trans. Signal Processing, V.49, p.2.314-2.324; J.Wang, J.Sun, S.Yu, "1-d and 2-d transforms from integers to integers", Proc. ICASSP'03, Hongkong, April 2003.

Как изложено в указанных работах, описанные в них целочисленные преобразования основываются на разложении преобразования на Givens-вращения и на применении известной схемы поднятия к Givens-вращениям, что влечет за собой проблему накопления ошибок округления. Это объясняется, в частности, тем, что в пределах одного преобразования должно многократно осуществляться округление, например, после каждого шага поднятия, так что особенно при длинных преобразованиях, которые сопровождаются соответственно большим количеством шагов поднятия, особенно часто должна проводиться операция округления. Как представлено, это приводит в результате к накоплению ошибок, а также к относительно высоким затратам на обработку, так как всегда после каждого шага поднятия осуществляется округление, чтобы выполнить следующий шаг поднятия.

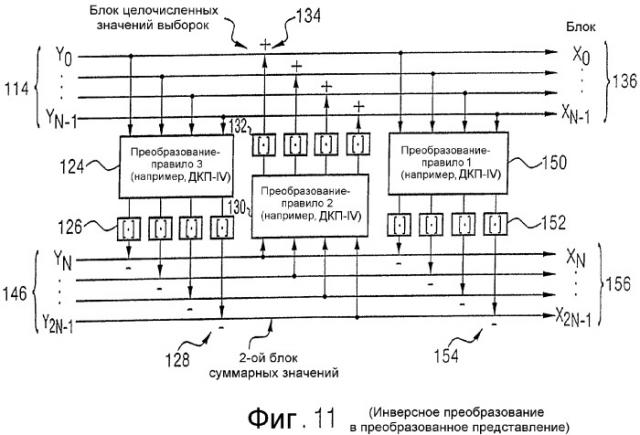
Далее, со ссылкой на фиг.9-11, еще раз представлено разложение взвешивания функцией окна по алгоритму МДКП, как оно описано в документе DE 10129240 А1, причем это разложение взвешивания по алгоритму МДКП на Givens-вращения с матрицами поднятия и соответствующими округлениями, предпочтительным образом, может комбинироваться с принципом, изображенным на фиг.1 для преобразования и на фиг.2 для обратного преобразования, чтобы получить полную целочисленную аппроксимацию МДКП, то есть целочисленное МДКП, согласно настоящему изобретению, причем на примере МДКП может быть реализован как принцип прямого преобразования, так и принцип обратного преобразования.

На фиг.3 показана обобщенная диаграмма соответствующего изобретению предпочтительного способа обработки дискретных по времени значений выборок, которые представляют аудиосигнал, чтобы получить целочисленные значения, на основе которых работает алгоритм целочисленного преобразования МДКП. Дискретные по времени значения выборок, посредством показанного на фиг.3 устройства, подвергаются взвешиванию функцией окна и дополнительно могут преобразовываться в спектральное представление. Дискретные по времени значения выборок, которые подаются на вход 10 устройства, взвешиваются посредством функции окна w с длиной, соответствующей 2N дискретным по времени значениям выборок, чтобы на выходе 12 получить целочисленные взвешенные значения выборок, которые пригодны для того, чтобы посредством преобразования, в частности устройством 14 для выполнения целочисленного ДКП, перевести их в спектральное представление. Целочисленное ДКП выполняется для того, чтобы из N входных значений сформировать N выходных значений, что отличается от функции МДКП 408 по фиг.6а, которая из 2N взвешенных значений выборок на основе уравнения МДКП вырабатывает только N спектральных значений.

Для взвешивания оконной функцией дискретных по времени значений выборок сначала в устройстве 16 выбираются два дискретных по времени значения выборок, которые совместно представляют вектор дискретных по времени значений выборок. Дискретное по времени значение выборки, которое выбирается с помощью устройства 16, расположено в первой четверти окна. Другое дискретное по времени значение выборки находится во второй четверти окна, как это более детально представлено с помощью фиг.5. К сформированному устройством 16 вектору применяется затем матрица вращения размерности 2 х 2, причем эта операция проводится не непосредственно, а посредством множества так называемых матриц поднятия.

Матрица поднятия имеет то свойство, что она имеет только один элемент, который зависит от окна w и не равен "1" или "0".

Факторизация волновых преобразований шагами поднятия представлена в публикации "Factoring Wavelet Transforms Into Lifting Steps", Ingrid Daubechies, Wim Sweldens, Preprint, Bell Laboratories, Lucent Technologies, 1996. В обобщенном смысле, схема поднятия представляет собой простое соотношение между идеально реконструируемыми парами фильтров, которые содержат одинаковые фильтры нижних частот или верхних частот. Каждая пара комплементарных фильтров может быть факторизована шагами поднятия. В частности, это справедливо для Givens-вращений. Можно рассмотреть случай, при котором полифазная матрица соответствует Givens-вращению. Тогда справедливо равенство:

Каждая из трех стоящих в правой части равенства матриц поднятия имеет в качестве элементов главной диагонали значение "1". Кроме того, в каждой матрице поднятия один элемент второстепенной диагонали равен "0" и один элемент второстепенной диагонали зависит от угла поворота α.

Вектор затем умножается на третью матрицу поднятия, то есть на крайнюю справа матрицу поднятия в приведенном выше равенстве, чтобы получить результирующий вектор. Это представлено на фиг.3 устройством 18. Затем первый результирующий вектор округляется с использованием любой функции округления, которая отображает множество действительных чисел на множество целых чисел, как представлено на фиг.3 устройством 20. На выходе устройства 20 получается округленный первый результирующий вектор. Округленный первый результирующий вектор вводится теперь в устройство 22 для его умножения на среднюю, то есть вторую, матрицу поднятия, чтобы получить второй результирующий вектор, который вновь округляется в устройстве 24, чтобы получить округленный второй результирующий вектор. Округленный второй результирующий вектор вводится теперь в устройство 26 для его умножения на приведенную слева в вышеуказанном уравнении, то есть на первую, матрицу поднятия, чтобы получить третий результирующий вектор, который, в итоге, вновь округляется в устройстве 28, чтобы получить на выходе 12 целочисленные взвешенные функцией окна значения выборок, которые затем, если желательно их спектральное представление, должны обрабатываться устройством 14, чтобы получить на спектральном выходе 30 целочисленные спектральные значения.

Предпочтительным образом, устройство 14 выполняется как устройство целочисленного ДКП.

Дискретное косинусное преобразование согласно типу 4 (ДКП-IV) с длиной N определяется следующим равенством:

Коэффициенты ДКП-IV образуют ортогональную матрицу размера N x N. Каждая ортогональная матрица размера N x N может быть разложена на N(N-1)/2 Givens-вращений, как это представлено в публикации P.P.Vaidyanathan, "Multirate Systems And Filter Banks", Prentice Hall, Englewood Cliffs, 1993. Следует отметить, что существуют и другие разложения.

Относительно классификации различных алгоритмов ДКП можно сослаться на работу H.S.Malvar, "Signal Processing With Lapped Transforms", Artech House, 1992. В общем, алгоритмы ДКП различаются по виду их базовой функции. В то время как алгоритм ДКП-IV, который здесь рассматривается в качестве предпочтительного, включает в себя несимметричные базовые функции, то есть четверть волны косинусоиды, 3/4 волны косинусоиды, 5/4 волны косинусоиды, 7/4 волны косинусоиды и т.д., дискретное косинусное преобразование, например, типа II (ДКП-II) имеет асимметричные и центрально симметричные базовые функции. 0-ая базовая функция имеет постоянную составляющую, первая базовая функция представляет собой полуволну косинусоиды, вторая базовая функция представляет собой полную косинусоиду и т.д. На основе того факта, что ДКП-II, в частности, учитывает постоянную составляющую, оно применяется при видеокодировании, но не при аудиокодировании, так как для аудиокодирования, в противоположность видеокодированию, постоянная составляющая не релевантна.

Далее описано, каким образом угол поворота α Givens-вращения зависит от оконной функции взвешивания.

МДКП с длиной окна 2N может быть сокращено до косинусного преобразования типа IV с длиной N. Это реализуется тем, что проводится операция TDAC в явном виде во временной области, и затем применяется ДКП-IV. При 50% перекрытии перекрывается левая половина окна для блока t с правой половиной предыдущего блока, то есть блока t-1. Перекрывающаяся часть двух следующих друг за другом блоков t-1 и t во временной области, то есть перед преобразованием, обрабатывается следующим образом, то есть между входом 10 и выходом 12 по фиг.3:

Обозначенные тильдой значения представляют собой значения на выходе 12 на фиг.3, в то время как значения х без тильды в вышеприведенном уравнении представляют собой значения на входе 10 или после устройства 16 для выбора. Индекс k изменяется от 0 до N/2-1, и w представляет собой оконную функцию взвешивания.

Из условия TDAC для оконной функции взвешивания w следует следующая взаимосвязь:

Для определенного угла α_k, где k=0, ..., N/2-1, эта предварительная обработка во временной области может описываться как Givens-вращение, как оно выполняется.

Угол α Givens-вращения зависит, следовательно, от оконной функции взвешивания w:

Следует отметить, что могут использоваться любые оконные функции взвешивания w, если они выполняют это условие TDAC.

Далее со ссылкой на фиг.4 описываются каскадный кодер и декодер. Дискретные по времени значения выборки от х(0) до x(2N-1), которые выделяются посредством окна, сначала выбираются таким образом с помощью устройства 16 на фиг.3, что выбираются значение выборки х(0) и значение выборки x(N-1), то есть значение выборки из первой четверти окна и значение выборки из второй четверти окна, чтобы сформировать вектор на выходе устройства 16. Пересекающиеся стрелки схематично представляют умножения поднятия с последующими округлениями устройств 18, 20, или 22, 24, или 26, 28, чтобы на входе блоков ДКП-IV получить целочисленные взвешенные оконной функцией значения выборок.

Когда первый вектор обработан, как описано выше, затем второй вектор из значений выборок x(N/2-1) и x(N/2), то есть вновь значение выборки из первой четверти окна и значение выборки из второй четверти окна, выбирается и обрабатывается посредством описанного на фиг.3 алгоритма. Аналогично этому обрабатываются все другие пары значений выборок из первой и второй четверти окна. Та же самая обработка проводится для третьей и четвертой четверти первого окна. После этого на выходе 12 имеется 2N взвешенных целочисленных значений выборок, которые теперь, как изображено на фиг.4, вводятся в преобразование ДКП-IV. В частности, взвешенные целочисленные значения выборок второй и третьей четверти вводятся в ДКП. Взвешенные целочисленные значения выборок первой четверти окна обрабатываются в предыдущем ДКП-IV вместе с взвешенными целочисленными значениями выборок четвертой четверти предыдущего окна. Аналогично этому четвертая четверть взвешенных целочисленных значений выборок на фиг.4 вместе с первой четвертью следующего окна вводятся в преобразование ДКП-IV. Среднее показанное на фиг.4 целочисленное преобразование ДКП-IV 32 вырабатывает N целочисленных спектральных значений от y(0) до y(N-1). Эти целочисленные спектральные значения могут теперь, например, просто энтропийно кодироваться, не требуя промежуточного квантования, так как взвешивание функцией окна и преобразование дают целочисленные выходные значения.

В правой половине фиг.4 представлен декодер. Декодер, состоящий из обратного преобразования и "инверсного оконного взвешивания", работает обратно по отношению к кодеру. Известно, что для обратного преобразования относительно ДКП-IV может применяться инверсное ДКП-IV, как показано на фиг.4. Выходные значения декодера ДКП-IV 34, как показано на фиг.4, теперь подвергаются инверсной обработке с соответствующими значениями предыдущего преобразования или последующего преобразования, чтобы из целочисленных взвешенных значений выборок на выходе устройства 34 или предыдущего и последующего преобразований вновь выработать дискретные по времени значения выборок аудиосигнала от х(0) до х(2N-1).

Операция на стороне выхода осуществляется посредством инверсного Givens-вращения, то есть таким образом, чтобы блоки 26, 28, или 22, 24, или 18, 20 проходились в противоположном направлении. Это более детально представлено с помощью второй матрицы поднятия уравнения (1). Если (в кодере) второй результирующий вектор формируется посредством перемножения округленного первого результирующего вектора с второй матрицей поднятия (устройство 22), то получается следующее выражение:

Значения х, y в правой стороне равенства (6) являются целыми числами. Однако это не имеет места для значения выражения x sin α. В этой связи нужно ввести функцию округления r, как это представлено следующим равенством:

Эту операцию выполняет устройство 24.

Инверсное отображение (в декодере) определяется следующим образом:

С помощью знака "минус" перед операцией округления показано, что целочисленная аппроксимация шага поднятия может обращаться, не вводя ошибок. Применение этой аппроксимации на каждом из трех шагов поднятия приводит к целочисленной аппроксимации Givens-вращения. Округленное вращение (в кодере) может претерпевать обращенное вращение (в декодере), не вводя ошибки, а именно тем, что инверсно округленные шаги поднятия проходятся в обратном порядке, то есть когда при декодировании алгоритм по фиг.3 проходится снизу вверх.

Если функция округления r является центрально симметричной, то инверсно округленное вращение идентично округленному вращению на угол -α и записывается следующим образом:

Матрица поднятия для декодера, то есть для инверсного Givens-вращения, получается в этом случае непосредственно из равенства (1), при этом только выражение "sin α" заменяется на выражение "-sin α".

Ниже со ссылкой на фиг.5 еще раз рассмотрено разложение обычного МДКП с перекрывающимися окнами 40-46. Окна 40-46 перекрываются, соответственно, на 50%. На каждое окно сначала выполняются Givens-вращения в пределах первой и второй четверти окна или в пределах третьей и четвертой четверти окна, как это схематично показано на фиг.5 стрелкой 48. Затем повернутые значения, то есть взвешенные функцией окна целочисленные значения выборок, вводятся в ДКП, реализующее преобразование из N в N (ДКП из N в N) таким образом, что всегда вторая и третья четверть окна или, соответственно, четвертая и первая четверть последующего окна совместно преобразуются в спектральное представление посредством ДКП-IV.

Затем обычные Givens-вращения разлагаются в матрицы поднятия, которые выполняются последовательно, причем после каждого умножения на матрицу поднятия выполняется шаг округления таким образом, что числа с плавающей запятой округляются непосредственно после их образования, так что перед каждым умножением результирующего вектора на матрицу поднятия результирующий вектор содержит только целые числа.

Выходные значения остаются, таким образом, всегда целочисленными, причем предпочтительным является также применение целочисленных входных значений. Это не является каким-то ограничением, так как любые значения выборок, например, сигнала с импульсно-кодовой модуляцией (ИКМ), как они сохранены, например, на компакт-диске (CD), являются целочисленными значениями, диапазон значений которых варьируется согласно длительности бита, то есть в зависимости от того, являются ли дискретные по времени цифровые входные значения 16-битовыми значениями или 24-битовыми значениями. Однако в том виде, как это выполнено, весь процесс является инвертируемым, то есть инверсные вращения выполняются в обратной последовательности. Таким образом, существует целочисленная аппроксимация МДКП с совершенной реконструкцией, то есть преобразование без потерь.

Показанное преобразование формирует на выходе целочисленные выходные значения вместо чисел с плавающей запятой. Оно обеспечивает совершенную реконструкцию, так что не вводятся никакие ошибки, если выполняется прямое, а затем обратное преобразование. Это преобразование, согласно предпочтительному варианту осуществления изобретения, заменяет модифицированное дискретное косинусное преобразование. Однако и другие способы преобразования могут выполняться в целочисленном виде, если возможны разложение на вращения и разложение вращений на шаги поднятия.

Целочисленное МДКП имеет большинство полезных свойств МДКП. Оно имеет структуру с перекрытием, за счет чего получается лучшая частотная избирательность, чем при блочных преобразованиях без перекрытия. На основе функции TDAC, которая учитывается уже при взвешивании функцией окна перед преобразованием, сохраняется критичное взятие выборок, так что общее число спектральных значений, которые представляют аудиосигнал, равно общему числу входных значений выборок.

Сравнение с нормальным МДКП, которое вырабатывает значения выборок с плавающей запятой, показывает при описанном предпочтительном целочисленном преобразовании, что только в спектральной области, в которой имеется низкий уровень сигнала, шум повышен по сравнению с нормальным МДКП, в то время как такое повышение шума не заметно при значительных уровнях сигнала. Зато целочисленная обработка обеспечивает эффективную реализацию в аппаратных средствах, так как применяются только шаги умножения, которые без труда могут разлагаться на шаги сдвига и суммирования, которые просто и быстро могут быть реализованы аппаратными средствами. Разумеется, также возможна реализация с помощью программного обеспечения.

Целочисленное преобразование обеспечивает хорошее спектральное представление аудиосигнала и при этом остается в области целых чисел. Если оно применяется к тональным частям аудиосигнала, то это приводит в результате к хорошей концентрации энергии. Тем самым можно сформировать эффективную схему кодирования без потерь, просто за счет того, что показанные на фиг.3 взвешивание функцией окна и преобразование каскадно связываются с энтропийным кодером. В частности, предпочтительным является поэтапное кодирование с применением значений перехода, как используется в MPEG AAC. Предпочтительным является то, что все значения масштабируются с понижением на определенную степень двух, пока они не будут согласованы с желательной кодовой таблицей, и затем отброшенные менее значимые биты дополнительно кодируются. По сравнению с альтернативой применения более крупных кодовых таблиц описанный вариант является более благоприятным в отношении требований к объему памяти для запоминания кодовых таблиц. Кодер, по существу, без потерь мог бы также быть получен благодаря тому, что определенные из наименее значимых битов просто отбрасываются.

В частности, для тональных сигналов энтропийное кодирование целочисленных спектральных значений обеспечивает высокий выигрыш при кодировании. Для переходных частей сигнала выигрыш при кодировании является низким, а именно ввиду равномерного спектра переходных сигналов, то есть ввиду незначительного числа спектральных значений, которые равны или близки к нулю. Как описано в работе J.Herre, J.D.Johnston: "Enhancing the Performance of Perceptual Audio Coders by Using Temporal Noise Shaping (TNS)" 101. AES Convention, Los Angeles, 1996, Preprint 4384, эта равномерность спектра применяется, однако, в том, что в частной области используется линейное предсказание. Альтернативным вариантом является прогнозирование в разомкнутом контуре. Другая альтернатива обеспечивается устройством прогнозирования с замкнутым контуром. Первый вариант, то есть устройство прогнозирования с разомкнутым контуром, называется TNS. Квантование после прогнозирования приводит к адаптации результирующих шумов квантования к временной структуре аудиосигнала и за счет этого предотвращает возникновение опережающего эха в психоакустических аудиокодерах. Для аудиокодирования без потерь подходит вторая альтернатива, то есть с устройством прогнозирования с замкнутым контуром, так как прогнозирование в замкнутом контуре обеспечивает более точную реконструкцию входного сигнала. Если этот метод применяется к вырабатываемому спектру, после каждого шага фильтра прогнозирования должно выполняться округление, чтобы оставаться в области целых чисел. За счет применения инверсного фильтра и той же самой функции округления можно снова точно восстановить первоначальный спектр.

Чтобы использовать избыточность между двумя каналами для сокращения данных, может также использоваться кодирование средней-боковой областей без потерь, если применяется округленное вращение на угол π/4. По сравнению с альтернативой вычисления суммы и разности левого и правого каналов стереосигнала округленное вращение имеет преимущество по получению энергии. Применение так называемых методов совместного стереокодирования может для каждой полосы включаться или исключаться, как это выполняется также согласно стандарту MPEG AAC. Другие углы поворота также могут учитываться для того, чтобы иметь возможность более гибко сократить избыточность между двумя каналами.

В частности, показанный на фиг.3 принцип преобразования обеспечивает целочисленную реализацию МДКП, то есть целочисленное МДКП, которое работает без потерь по отношению к прямому преобразованию и обратному преобразованию. Кроме того, за счет этапов округления 20, 24, 28 и соответствующих этапов округления в целочисленном ДКП (блок 14 на фиг.3) все еще возможна целочисленная обработка, то есть обработка с более грубо квантованными значениями, чем они, например, формировались при умножении с плавающей запятой с матрицей поднятия (блоки 18, 22, 26 на фиг.3).

Это приводит к тому, что все целочисленное МДКП также может выполняться эффективным вычислительным образом.

Отсутствие потерь этого целочисленного МДКП, говоря в общем, отсутствие потерь всего алгоритма кодирования, обозначаемого как кодирование без потерь, объясняется тем, что сигнал, когда он кодируется, чтобы получить кодированный сигнал, и когда он снова декодируется, чтобы получить кодированный/декодированный сигнал, выглядит точно так, как первоначальный сигнал. Иными словами, первоначальный сигнал идентичен кодированному/декодированному первоначальному сигналу. Это явно противоположно так называемому кодированию с потерями, при котором, как в случае аудиокодеров, которые работают на психоакустической основе, за счет процесса кодирования и особенно за счет процесса квантования, которое управляется психоакустической моделью, данные безвозвратно теряются.

Однако, разумеется, вводятся ошибки округления. Так проводятся этапы округления, как показано на фиг.3 в блоках 20, 24, 28, которые, разумеется, вводят ошибку округления, которая вновь "исключается" только в декодере, когда выполняются обратные операции. Таким образом, принципы кодера/декодера без потерь принципиально отличаются от концепций кодера/декодера с потерями тем, что в случае концепций кодера/декодера без потерь ошибка округления вводится таким образом, что она может вновь исключаться, в то время как в случае концепции кодера/декодера с потерями это не имеет места.

Однако если рассматривается кодированный сигнал, то есть в примере кодеров с преобразованием - спектр блока временных значений выборок, то округление при прямом преобразовании или, в общем случае, квантование такого сигнала приводит к тому, что в сигнал вводится ошибка. Тем самым на идеальный спектр сигнала без ошибок накладывается ошибка округления, которая в типовом случае, например в примере по фиг.3, представляет собой белый шум, который равномерно окружает все частотные составляющие рассматриваемой области спектра. Этот наложенный на идеальный спектр белый шум представляет собой, таким образом, ошибку округления, которая возникла, например, из-за округления в блоках 20, 24, 28 во время взвешивания функцией окна, то есть предварительной обработки сигнала, перед собственно обработкой ДКП в блоке 14. Особенно следует отметить то, что для требования отсутствия потерь вся ошибка округления обязательно должна кодироваться, то есть должна переноситься к декодеру, так как декодеру необходима вся введенная в кодере ошибка округления, чтобы вновь обеспечить корректное восстановление без потерь.

Ошибка округления, правда, не создает проблем, если возникает не в спектральном представлении, то есть когда спектральное представление только переносится в сохраненном виде и вновь декодируется посредством корректно согласованного инверсного декодера. В таком случае всегда выполняется критерий отсутствия потерь, независимо от того, сколько ошибок округления введено в спектр. Если, однако, со спектральным представлением, то есть с идеальным спектральным представлением, подверженным влиянию ошибок округления, первоначального сигнала что-то предпринимается, например формируются уровни масштабируемости и т.д., то все эти вещи функционируют тем лучше, чем меньше ошибка округления.

Таким образом, при кодировании/декодировании также существует требование, что сигнал, с одной стороны, должен быть восстанавливаемым без потерь посредством специального декодера, что сигнал, однако, должен иметь наименьшую возможную ошибку округления в спектральном представлении, чтобы сохранить в значительной степени гибкость, что спектральное представление также может вводиться в неидеальные декодеры без потерь или могут формироваться уровни масштабирования и т.д.

Как уже отмечено, ошибка округления проявляется как белый шум по всему рассматриваемому спектру. С другой стороны, особенно в применениях, характеризуемых высоким качеством, особенно интересных в варианте без потерь, а также в аудиоприложениях с очень высокими частотами выборок, например 96 кГц, аудиосигнал имел бы разумное содержание только в определенной спектральной области, которая могла бы доходить максимум до 20 кГц. В типовом случае область, в которой концентрируется максимальная энергия аудиосигнала, будет областью между 0 и 10 кГц, в то время как в области выше 10 кГц энергия сигнала уже значительно спадает. Однако для шума, введенного округлением, это соотношение является безразличным. Он накладывается на весь рассматриваемый спектральный диапазон энергии сигнала. Это приводит к тому, что в спектральных областях, то есть в типичном случае, в высоком спектральном диапазоне, где аудиосигнал отсутствует или имеется лишь очень малое количество энергии аудиосигнала, будет иметь место только ошибка округления. Ошибка округления, в частности, ввиду своего недерминированного характера, к тому же вызывает пробле