Способ сопровождения групповой воздушной цели

Способ сопровождения групповой воздушной цели

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области вторичной цифровой обработки радиолокационных сигналов и может быть использовано для сопровождения разрешаемых по доплеровской частоте элементов групповой воздушной цели (ГВЦ) и распознавания количества целей в группе, а также варианта динамики их полета (например, распознавание поведенческой активности по принципу «стационарный полет-маневр в группе - маневр составом группы - отделение от группы»; функционального назначения целей в группе по принципу «ведущий-ведомый» в различных формах боевых порядков (БП) «пеленг», «клин», «фронт»).

Известен способ сопровождения ГВЦ, заключающийся в отслеживании ее центроида (среднего кинематического поведения группы) и боковых траекторий, распознавании на основе сравнения переменных состояния центральной и боковых траекторий отделяющихся целей от группы [1].

Недостатком данного способа сопровождения ГВЦ являются его ограниченные функциональные возможности по распознаванию состояния ГВЦ, под которым в дальнейшем понимается определение количества разрешаемых на основе узкополосной доплеровской фильтрации целей в группе и варианта динамики их полета (поведенческой активности, функционального назначения самолетов в группе, формы БП).

Известен способ сопровождения ГВЦ, основанный на процедуре оптимальной многомерной линейной дискретной калмановской фильтрации, применяемой для сопровождения разрешаемых по доплеровской частоте элементов ГВЦ и описываемой следующими выражениями [2]

где

k=0, 1, ... - номер такта работы фильтра;

P^-(k+1) и P(k+1) - ковариационные матрицы ошибок экстраполяции и фильтрации соответственно;

Ф(k) - переходная матрица состояния;

Q(k+1) и R(k+1) - ковариационные матрицы шумов возбуждения и наблюдения соответственно;

K(k+1) - матрица весовых коэффициентов;

I - единичная матрица;

и - вектор текущих и экстраполированных оценок доплеровских частот;

H(k) - матрица наблюдения;

Y(k) - вектор наблюдения отсчетов доплеровских частот;

Z(k+1) - матрица невязок измерения;

ψ(k+1) - матрица априорных ошибок фильтрации;

"-1" - операция вычисления обратной матрицы;

"т" - операция транспонирования матрицы.

Недостатком данного способа сопровождения ГВЦ являются его ограниченные функциональные возможности по распознаванию состояния элементов ГВЦ на этапе их сопровождения по доплеровской частоте.

Целью предлагаемого изобретения является расширение функциональных возможностей по распознаванию состояния элементов ГВЦ на этапе их сопровождения по доплеровской частоте.

Для достижения этой цели в способе сопровождения разрешаемых по доплеровской частоте элементов ГВЦ, основанном на процедуре оптимальной многомерной линейной дискретной калмановской фильтрации, описываемой выражениями (1)-(6), дополнительно аналогичная процедура оптимальной многомерной линейной дискретной калмановской фильтрации (выражения (1)-(6)) осуществляется не в одном, а параллельно в каждом оптимальном фильтре ОФ_mj их матрицы,

где

m=1, М; М - максимальное количество разрешаемых по доплеровской частоте элементов ГВЦ;

j=1, L; L - количество вариантов динамики полета m элементов ГВЦ, при различных априорных данных, принятых при фильтрации в каждом ОФ_mj относительно количества m разрешаемых по доплеровской частоте целей в группе и j варианте динамики их полета в различных формах БП, при этом по строкам матрицы оптимальных фильтров располагаются фильтры, в которых в качестве априорных сведений приняты динамические модели для различных гипотез относительно количества m разрешаемых по доплеровской частоте целей в группе, а по столбцам - фильтры с динамическими моделями для различных гипотез относительно j-x вариантов динамики полета целей в различных формах БП,

для каждого оптимального фильтра их матрицы производится вычисление соответствующих значений случайной величины l² _mj(k+1) в соответствии с выражением

осуществляется сравнение полученных величин l² _mj(k+1) с соответствующими граничными значениями «хи-квадрат» χ² _{гр m}(m, P_ош), одинаковыми для всех оптимальных фильтров, находящихся в m-й строке (m=1, М) их матрицы,

где Р_ош - вероятность ошибки в том, что правильная гипотеза относительно количества m разрешаемых по доплеровской частоте целей будет отвергнута, определяется максимальный номер строки матрицы оптимальных фильтров, где находится один и более оптимальных фильтров, для которых выполняется условие (8), что соответствует оценке количества m целей, разрешаемых по доплеровской частоте,

для тех оптимальных фильтров для которых в -й строке их матрицы выполняется условие (8), производится вычисление соответствующих значений обобщенных дисперсий реальных ошибок фильтрации в соответствии с выражением

определяется номер столбца в строке где находится оптимальный фильтр, для которого величина минимальна, что соответствует оценке варианта динамики полета оцененного количества элементов ГВЦ в соответствующей для данного оптимального фильтра форме БП, на основе значений и осуществляется выбор оценок доплеровских частот с выхода только одного из их матрицы, находящегося на пересечении оцененных номера строки и столбца (т.е. после принятия решения относительно количества разрешаемых по доплеровской частоте элементов ГВЦ и варианта динамики их полета в различных формах БП).

Новыми признаками, обладающими существенными отличиями, являются:

1. Распознавание в процессе параллельного сопровождения на основе процедуры оптимальной многомерной линейной дискретной калмановской фильтрации (выражения (1)-(6)) количества разрешаемых по доплеровской частоте элементов ГВЦ (по критерию хи-квадрат Пирсона (выражения (7), (8)) и варианта динамики их полета в различных формах БП (по критерию минимума обобщенной дисперсии реальных ошибок фильтрации, вычисляемой в соответствии с выражением (9)).

2. Выбор оценки отслеживаемых доплеровских частот с выхода только одного оптимального фильтра из их матрицы, находящегося на пересечении оцененных номера строки и столбца (т.е. после принятия решения относительно количества разрешаемых по доплеровской частоте элементов ГВЦ и варианта динамики их полета в различных формах БП).

Данные признаки обладают существенными отличиями, т.к. в известных способах не обнаружены.

Применение всех новых признаков позволит не только сопровождать разрешаемые по доплеровской частоте элементы ГВЦ, но и распознавать их количество и динамику полета, например поведенческую активность по принципу «стационарный полет-маневр в группе - маневр составом группы - отделение от группы»; функциональное назначение целей в группе по принципу «ведущий-ведомый» в формах БП «пеленг», «клин», «фронт».

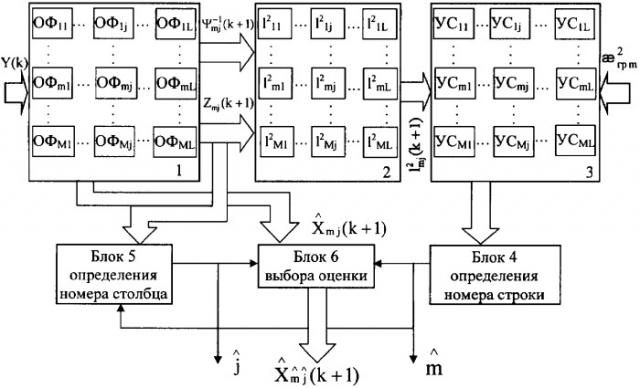
На чертеже приведена блок-схема, поясняющая предлагаемый способ сопровождения ГВЦ.

На вход блока 1 оценок на каждом k такте поступает m (m=1, М) отсчетов доплеровских частот, обусловленных j-м (j=1, L) вариантом динамики полета элементов ГВЦ, т.е. формируется вектор наблюдения Y(k) в выражении (4) при сложной гипотезе Г_mj (m=1, М; j=1, L) о том, что при m разрешаемых по доплеровской частоте целей в группе имеет место j-й вариант динамики их полета.

Блок 1 оценок представляет собой матрицу оптимальных фильтров, в каждом из которых ОФ_mj (m=1, М; j=1, L) реализована в соответствии с выражениями (1)-(6) процедура оптимальной многомерной линейной дискретной калмановской фильтрации. Для осуществления параллельной фильтрации наблюдаемых отсчетов доплеровских частот соответствующие входы ОФ объединены (первые, вторые и т.д). Фильтрация разрешаемых доплеровских частот в каждом ОФ_mj их матрицы осуществляется при различных априорных данных, принятых при фильтрации в соответствующем оптимальном фильтре относительно количества m разрешаемых по доплеровской частоте целей в группе и j варианте динамики их полета в различных формах БП. При этом по строкам матрицы оптимальных фильтров располагаются фильтры, в которых в качестве априорных сведений приняты динамические модели для простых гипотез Г_m (m=1, М) относительно количества m разрешаемых по доплеровской частоте целей в группе, а по столбцам - фильтры с динамическими моделями для простых гипотез Г^(m) _j (j=1, L) относительно j-x вариантов динамики полета целей в различных формах БП при принятой гипотезе Г_m. Динамические модели, принятые при фильтрации в каждом ОФ_mj их матрицы (m=1, М; j=1, L) в виде различных структур матриц Ф_mj(k) и Q_mj(k+1) с соответствующими численными значениями их элементов, выполняют роль динамического эталона, поскольку они одновременно являются априорными сведениями не только для сопровождения элементов ГВЦ, но и для распознавания их состояния. Исходя из этого, при многогипотезном сопровождении элементов ГВЦ и последующем распознавании их состояния будет иметь место структурная и параметрическая неопределенности, обусловленные соответственно многогипотезностью относительно количества разрешаемых по доплеровской частоте целей в группе Г_m (m=1, М) и динамики их полета Г_m (m=1, М; j=1, L).

Разрешение структурной неопределенности в предлагаемом способе осуществляется по критерию хи-квадрат Пирсона, согласно которого для каждого ОФ_mj их матрицы (m=1, М; j=1, L) в вычислителе 2 величин l² на основе значений элементов матрицы невязок измерения Z_mj(k+1) (выражение (4)) и матрицы априорных ошибок фильтрации Ψ_mj(k+1) (выражение (2)), поступающих с блока 1 оценок, производится вычисление соответствующих значений l² _mj(k+1) в соответствии с выражением (7). В блоке 3 сравнения в соответствующем для каждого ОФ_mj устройстве сравнения УС_mj осуществляется сравнение (выражение (8)) полученных величин l² _mj(k+1) с соответствующими значениями χ² _{гр m}(m, Р_ош), одинаковыми для всех оптимальных фильтров, находящихся в m-й строке их матрицы. По результатам сравнения в блоке 4 определения номера строки находится максимальный номер строки матрицы оптимальных фильтров, где расположен один и более , для которых выполняется условие (8), что соответствует оценке количества целей, разрешаемых по доплеровской частоте. Поскольку условие (8) может быть выполнено одновременно в нескольких оптимальных фильтрах в -й строке матрицы, то из этого следует, что по критерию хи-квадрат Пирсона может быть разрешена только структурная неопределенность.

Разрешение параметрической неопределенности в предлагаемом способе осуществляется по критерию минимума обобщенной дисперсии реальных ошибок фильтрации следующим образом. Для тех оптимальных фильтров, находящихся в оцененном номере строки их матрицы и для которых выполняется условие (8), в блоке 5 определения номера столбца производится вычисление соответствующих значений обобщенных дисперсий реальных ошибок фильтрации в соответствии с выражением (9) и определяется номер столбца в строке где находится ОФ, для которого величина минимальна, что и будет соответствовать оценке варианта динамики полета оцененного количества элементов ГВЦ в соответствующей для данного ОФ форме боевого порядка. На основе значений и в блоке 6 выбора оценки, куда поступают оценки (m=1, М; j=1, L) с выходов всех оптимальных фильтров, осуществляется выбор оценок доплеровских частот с выхода только одного из их матрицы, в котором динамический эталон по критериям хи-квадрат Пирсона и минимума обобщенной дисперсии реальных ошибок фильтрации будет наилучшим образом соответствовать реальному количеству разрешаемых по доплеровской частоте элементов ГВЦ и реальной динамике их полета на входе блока 1 оценок. Таким образом, оценка вектора формируется на выходе только после принятия решения об истинности сложной гипотезы Г_mj (m=1, М; j=1, L).

Примеры технических устройств, реализующих предложенный способ сопровождения ГВЦ, приведены в [3, 4, 5]. Так, в [3] приведено устройство, в котором осуществляется сопровождение ГВЦ, состоящей из пары самолетов (m=2), и распознавание поведенческой активности (по принципу «стационарный полет пары - маневр в паре - маневр составом пары» (j=1, 2, 3)) по критерию минимума обобщенной дисперсии реальных ошибок фильтрации (выражение (9)). В [4] приведено устройство, в котором осуществляется сопровождение ГВЦ, состоящей из четырех самолетов (m=4), и распознавание формы БП с его параметрами (по принципу «пеленг-клин-фронт») также по критерию минимума обобщенной дисперсии реальных ошибок фильтрации (выражение (9)). При этом количество ОФ равно 72×L (где L - количество вариантов набора параметров полета ГВЦ, состоящей из четырех самолетов, в каждой форме БП). В [5] приведено устройство, в котором осуществляется сопровождение одиночной цели и ГВЦ, состоящей из двух, трех и четырех самолетов (m=1, 2, 3, 4), и распознавание количества целей в группе по критерию хи-квадрат Пирсона (выражения (7) и (8)) и формы БП с его параметрами (по принципу «пеленг-клин-фронт») по критерию минимума обобщенной дисперсии реальных ошибок фильтрации (выражение (9)). При этом количество ОФ в каждой строке их матрицы является различным.

При математическом моделировании работы устройств, реализующих предлагаемый способ, на их вход подавались дискретные отсчеты доплеровских частот, полученные в результате узкополосной доплеровской фильтрации (полоса пропускания доплеровского фильтра составляла 10 Гц) и статистической обработки радиолокационных сигналов, отраженных от реальных ГВЦ и летящих в различных формах сомкнутых БП (интервал, дистанция составляли 20-500 м). Динамические эталоны (модели), принятые при фильтрации в каждом оптимальном фильтре ОФ_mj их матрицы, представляли собой линейные стохастические дифференциальные уравнения, структуры и численные значения параметров модели определялись на основе анализа траекторных статистических характеристик радиолокационных сигналов, отраженных от реальных ГВЦ. При этом неадекватность по траекторным статистическим характеристикам моделей реальному полету элементов ГВЦ не превышала 12%. Дискретность изменения численных значений параметров динамических моделей от фильтра к фильтру составляла 6-8%. В результате моделирования при отношениях сигнал/шум 14-24 дБ получены следующие обобщенные характеристики устройств, реализующих предлагаемый способ.

Точность сопровождения элементов ГВЦ по доплеровской частоте (СКО оценки доплеровской частоты) - 0,36-1,55 Гц.

Вероятность ошибки в оценке количества разрешаемых по доплеровской частоте элементов ГВЦ - не более 0,005.

Вероятность распознавания поведенческой активности элементов ГВЦ по принципу «стационарный полет-маневр в группе-маневр составом группы) - 0,75-0,98 (вероятность ложного распознавания - не более 0,01).

Вероятность распознавания формы БП по принципу «пеленг-клин-фронт» и функционального назначения самолетов в группе по принципу «ведущий-ведомый» - 0,96-0,98 (вероятность ложного распознавания - не хуже 10^-4).

Время распознавания - не более 3,5 с.

Таким образом, применение предлагаемого изобретения позволит расширить функциональные возможности по распознаванию состояния элементов ГВЦ (определить количество целей в группе, их поведенческую активность, форму боевого порядка и функциональное назначение самолетов в нем) на этапе их сопровождения по доплеровской частоте.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Фарина А., Студер Ф. Цифровая обработка радиолокационной информации. Сопровождение целей. / Пер. с англ. - М.: Радио и связь, 1993, с.246-248 (аналог).

2. Казаринов Ю.М., Соколов А.И., Юрченко Ю.С. Проектирование устройств фильтрации радиосигналов. - Л.: изд. Ленинградского университета, 1985, с.150-151 (прототип).

3. Патент РФ на изобретение №2084921, 1997.

4. Патент РФ на изобретение №2123709, 1998.

5. Патент РФ на изобретение №2166771, 2001.

Способ сопровождения разрешаемых по доплеровской частоте элементов групповой воздушной цели, заключающийся в вычислении процедуры оптимальной многомерной линейной дискретной калмановской фильтрации, описываемой выражениями

где k=0, 1, ... - номер такта работы фильтра;

P^-(k+1) и P(k+1) - ковариационные матрицы ошибок экстраполяции и фильтрации соответственно;

Ф(k) - переходная матрица состояния;

Q(k+1) и R(k+1) - ковариационные матрицы шумов возбуждения и наблюдения соответственно;

K(k+1) - матрица весовых коэффициентов;

I - единичная матрица;

и - вектор текущих и экстраполированных оценок доплеровских частот;

H(k) - матрица наблюдения;

Y(k) - вектор наблюдения отсчетов доплеровских частот;

Z(k+1) - матрица невязок измерения;

Ψ(k+1) - матрица априорных ошибок фильтрации;

"-1" - операция вычисления обратной матрицы;

"т" - операция транспонирования матрицы,

отличающийся тем, что процедура оптимальной многомерной линейной дискретной калмановской фильтрации, описываемая выражениями (1)-(6), осуществляется не в одном, а параллельно в каждом оптимальном фильтре ОФ_mj их матрицы,

где m=1, М;

М - максимальное количество разрешаемых по доплеровской частоте элементов групповой воздушной цели;

j=1, L;

L - количество вариантов динамики полета m элементов групповой воздушной цели,

при различных априорных данных, принятых при фильтрации в каждом ОФ_mj относительно количества m разрешаемых по доплеровской частоте целей в группе и j варианте динамики их полета в различных формах боевого порядка, при этом, по строкам матрицы оптимальных фильтров располагаются фильтры, в которых в качестве априорных сведений приняты динамические модели для различных гипотез относительно количества m разрешаемых по доплеровской частоте целей в группе, а по столбцам - фильтры с динамическими моделями для различных гипотез относительно j вариантов динамики полета целей в различных формах боевого порядка, для каждого оптимального фильтра их матрицы производится вычисление соответствующих значений l² _mj(k+1) в соответствии с выражением

осуществляется сравнение полученных величин l² _mj(k+1) с соответствующими значениями χ² _{гр m}(m, Р_ош), одинаковыми для всех оптимальных фильтров, находящихся в m-й строке их матрицы,

где Р_ош - вероятность ошибки в том, что правильная гипотеза относительно количества m разрешаемых по доплеровской частоте целей будет отвергнута, определяется максимальный номер строки матрицы оптимальных фильтров, где находится один и более оптимальных фильтров, для которых выполняется условие (8), что соответствует оценке количества m целей, разрешаемых по доплеровской частоте,

для тех оптимальных фильтров для которых в строке их матрицы выполняется условие (8), производится вычисление соответствующих значений обобщенных дисперсий реальных ошибок фильтрации в соответствии с выражением

определяется номер столбца в строке , где находится оптимальный фильтр, для которого величина минимальна, что соответствует оценке варианта динамики полета оцененного значения элементов групповой воздушной цели в соответствующей для данного оптимального фильтра форме боевого порядка,

на основе значений и осуществляется выбор оценок доплеровских частот с выхода только одного из их матрицы, находящегося на пересечении оцененных номера строки и столбца .