Разностно-дальномерный способ пеленгования источника радиоизлучения

Разностно-дальномерный способ пеленгования источника радиоизлучения

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники и может быть использовано в пеленгационных комплексах для определения угловых координат источника радиоизлучения (ИРИ).

Современные системы определения направления на ИРИ построены с использованием известных способов пеленгования: амплитудного (метод максимума, метод минимума, метод сравнения и др.), фазового, частотного и временного.

Известны способы и устройства пеленгования [1-5, 10-20 и др.].

Так, например, известен ряд способов пеленгования, основанных на том, что фазовые соотношения между сигналами, принимаемыми в пространственно разнесенных точках, можно преобразовать в амплитудную зависимость суммы принятых сигналов от местоположения ИРИ.

Наиболее очевидным и широко применяемым является амплитудный способ пеленгования, при котором используется антенная система, имеющая диаграмму направленности с ярко выраженным максимумом. За счет механического изменения положения (ориентации) антенны осуществляется сканирование пространства, в результате чего определяется положение антенны, при котором выходной сигнал антенны имеет максимальную амплитуду, а направление, совпадающее с максимумом диаграммы направленности антенны, принимается за направление на ИРИ.

Этот способ пеленгования можно рассматривать как вырожденный случай разностно-дальномерного способа, когда за счет механического перемещения антенной системы подбирается такое ее положение, чтобы разности дальностей от ИРИ до симметричных точек антенны были равны нулю (а следовательно, и разности фаз сигналов, приходящих в эти точки, были равны нулю). Синфазное сложение сигналов, пришедших по различным траекториям, обеспечивает максимум энергии в точке приема.

Основным недостатком такого способа является необходимость механического перемещения антенной системы или, по крайней мере, ее отдельных элементов (например, облучателя).

Известен также способ пеленгования на основе измерения разности времен приема сигналов от ИРИ двумя разнесенными антеннами [например, 6]. При отклонении положения ИРИ от перпендикуляра к центру базы возникает разность хода сигналов Δr=r₁-r₂ (r₁ и r₂ - расстояния от ИРИ до первой и второй антенн соответственно). Относительное запаздывание τ сигналов вследствие постоянства скорости и прямолинейности распространения радиоволн пропорционально разности хода

τ=Δr/с.

Значение азимута α ИРИ вычисляется по формуле

α≈arccos(Δr/d),

где d - расстояние между антеннами,

при этом

где r=min(r₁, r₂).

В общем случае системы, использующие рассмотренный принцип, являются разностно-дальномерными, однако при больших удалениях ИРИ от центра базы, когда расстояние до ИРИ существенно превышает размер базы, гиперболические линии положения, свойственные разностно-дальномерному способу, в дальней зоне практически совпадают с их асимптотами, исходящими в виде лучей из центра базы. В этом случае разностно-дальномерные системы допустимо считать угломерными.

Пеленгование возможно так же произвести на основе измерения доплеровского смещения частоты Δf_д [см., например, 7]. Поскольку

Δf_д=-ν_r/λ,

где λ - длина волны сигнала ИРИ;

ν_r - радиальная скорость ИРИ относительно приемной антенны,

то, измеряя Δf_д на предельно малом интервале, можно получить вариант частотного способа, именуемый доплеровским дифференциальным, который позволяет определить значение углового параметра местоопределения α:

α=2arccos(ν_r/ν),

где ν - скорость движения ИРИ в системе координат, начало которой совпадает с точкой расположения приемной антенны.

Такой подход к измерению угла основан на допущении о том, что при малых измерительных базах («малых» по сравнению с расстоянием до лоцируемого объекта) гиперболическая поверхность положения асимптотически стремится к конической, форма которой в свою очередь однозначно описывается точкой вершины и углом при основании.

Основными недостатками перечисленных способов является возможность пеленгования ИРИ только в дальней зоне, т.е. при выполнении условия

r>>d,

где r - расстояние до ИРИ;

d - длина измерительной базы.

Выполнение данного условия позволяет принять допущение о плоскости фронта распространения электромагнитной волны.

Известно, что точность определения пеленга ИРИ зависит от величины отношения размера измерительной базы к величине дальности до ИРИ (зависимость характеризуется выражением, учитывающим нижнюю границу Крамера-Рао [6]). Однако значительное увеличение размера измерительной базы приводит к росту систематической погрешности пеленгования, обусловленной сферичностью фронта электромагнитной волны. Величина ошибки пеленгования при значениях дальности r<10d может достигать десяти и более процентов от значения угловой координаты ИРИ. Для снижения погрешности пеленгования используют пеленгационные устройства (например, [20]), в которых систематическая погрешность пеленгования сводится к минимуму за счет учета сферичности волнового фронта.

Из известных способов пеленгования наиболее близким к предлагаемому является способ [20], который предполагает выполнение следующих операций:

- располагают три антенны в вершинах треугольника ΔАВС:

- принимают сигнал ИРИ на все три антенны;

- измеряют разности времен Δt_AC и Δt_BC приема сигнала ИРИ антеннами, размещаемыми в парах точек {A, C} и {B, C} соответственно;

- вычисляют значение γ азимута ИРИ с использованием выражения

где x₃=(b²-c²)/a;

- вычисляют координаты {x_f, y_f} точки F, принадлежащей линии пеленга ИРИ, с использованием выражений:

где

- отображают полученные результаты.

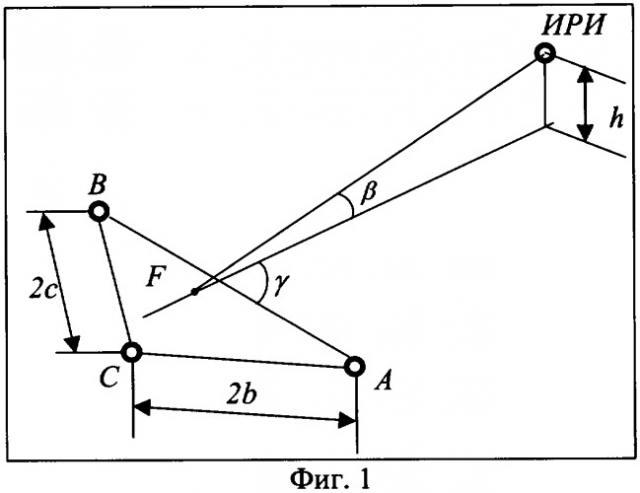
Недостаток данного способа пеленгования состоит в том, что определяется только одна угловая координата ИРИ - азимут, тогда как для однозначного определения линии пеленга ИРИ необходимо определить также угол места β (см. фиг.1)

Данный способ выбран в качестве прототипа.

Целью изобретения является разработка способа, позволяющего вычислять угол β - угол места ИРИ.

Поставленная цель достигается тем, что в способе пеленгования ИРИ, основанном на приеме его сигнала тремя антеннами, образующими две пары измерительных баз, измерении разностей времен прихода сигнала ИРИ на антенны и вычислении с помощью используемых в прототипе выражений (приведенных выше):

- значений разностей дальностей от ИРИ до пар точек {A, C} и {B, C} размещения антенн;

- значения угла γ азимута ИРИ;

- координат {x_f, y_f} точки F, принадлежащей линии пеленга ИРИ,

дополнительно вычисляют значение угла места β ИРИ с использованием выражения

где

и отображают полученные результаты.

Предлагаемый способ предполагает выполнение следующих операций:

- располагают три антенны в вершинах треугольника ΔАВС;

- принимают сигнал ИРИ на все три антенны;

- измеряют разности времен приема сигнала ИРИ антеннами, образующими измерительные базы [А, С} и {В, С];

- вычисляют значение угла γ азимута ИРИ;

- вычисляют значение координат точки, принадлежащей линии положения ИРИ;

- вычисляют значение угла β места ИРИ;

- отображают полученные результаты.

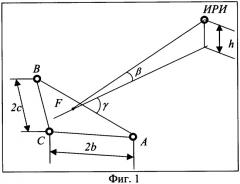
Устройство, реализующее данный способ пеленгования, аналогично устройству, описанному в [20], и состоит из трех функционально взаимосвязанных элементов (фиг.2):

- антенной системы, содержащей три антенны 1, 2 и 3;

- системы измерения, содержащей блоки 4 и 5, предназначенные для измерения разностей времен приема сигнала ИРИ парами антенн {1; 3} и {2; 3};

- системы обработки и отображения, содержащей вычислительный блок 6 и блок 7, осуществляющий визуализацию результатов.

Отличие от устройства, описанного в [20], состоит в том, что в вычислительном блоке 6 осуществляется также вычисление значения угла места β.

Принцип работы устройства, реализующего предлагаемый способ, состоит в следующем: антенны 1, 2 и 3 располагают в трех точках трехмерного пространства А, В, С, имеющих координаты <x_A, y_A, z_A>, <x_B, y_B, z_B> и <х_C, y_C, z_C>, соответственно.

Для удобства и наглядности дальнейшего изложения предположим, что точка расположения ИРИ совпадает с некоторой точкой D, имеющей неизвестные координаты <x, y, z>. Обозначим разность расстояний от нее до точек А и В через Δr_AB, а разность расстояний до точек А и С через Δr_AC.

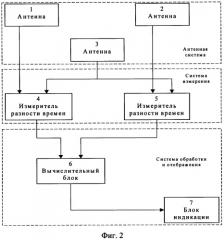
Введем в рассмотрение систему координат Oxyz, заданную таким образом, чтобы ее начало совпадало с серединой отрезка АВ, ось Ох была коллинеарная вектору , а плоскость хОу совпадала с плоскостью АВС (фиг.3). Тогда координаты точек А, В и С в системе Oxyz соответственно равны

х_A=-a; у_A=0; z_A=0;

x_B=a; y_B=0; z_B=0;

x_C=x₃; y_C=y₃; z_C=0;

где

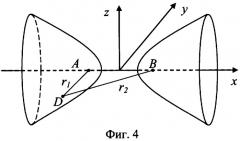
В данной системе координат, в соответствии с [20], уравнение поверхности положения точки D имеет вид канонического уравнения двуполостного гиперболоида вращения (см. фиг.4)

где

Аналогично, введя в рассмотрение систему координат О'х'у'z', начало которой совпадает с серединой отрезка АС, ось O'х' коллинеарна полупрямой АС, а плоскость х'O'у' совпадает с плоскостью Oxyz, можно получить, что точка D принадлежит поверхности, описываемой уравнением

где

х', у', z' - координаты точки D в системе координат O'х'у'z'.

Поскольку точка D принадлежит одновременно двум поверхностям, следовательно, она принадлежит линии пересечения этих поверхностей.

Поскольку плоскости хОу и х'О'у' совпадают, то уравнение (2) в системе координат Oxyz можно получить, произведя замену переменных в соответствии с известными выражениями [8]:

х'=(х-x₀)cosα+(у-у₀)sinα,

у'=-(х-x₀)sinα+(у-y₀)cosα,

где x₀, y₀ - координаты точки O'х' в системе координат Oxyz;

α - угол между координатными осями Ох и O'х' (см. фиг.5).

В результате такого преобразования уравнение (2) примет вид

a₂х²+b₂у²+с₂ху+d₂x+е₂у+f₂=z²,

где а₂=(а+х₃)²/Δr² _AC - 1;

b₂=y² ₃/Δr² _AC - 1;

c₂=2y₃(a+x₃)/Δr² _AC;

d₂=x₃-a-2(a+x₃)(2b²-a(a+х₃))/Δr² _AC;

e₂=y₃-2y₃(2b²-a(a+x₃))/Δr² _AC;

f₂=(2b²-a(a+x₃))²/Δr² _AC-((a-x₃)²+y² ₃+4b²-Δr² _AC)/4;

Если рассмотреть разность разностей расстояний от точки D до пар точек {А, В} и {А, С}, то очевидно, что

то есть разность разностей расстояний от точки D до пар точек {А, В} и {А, С} равна разности расстояний от точки D до пары точек {С, В}. Из чего следует, что точка D также принадлежит и третьей поверхности, описываемой уравнением

а₃х²+b₃y²+с₃ху+d₃x+е₃у+f₃=z²,

где а₃=(а-х₃)²/Δr² _BC - 1;

b₃=y₃ ²/Δr² _BC - 1;

c₃=-2y₃(a-x₃)/Δr² _BC;

d₃=x₃+a+2(а-х₃)(2c²-а(а-х₃))/Δr² _BC;

e₃=y₃-2y₃(2c²-a(a-x₃))/Δr² _BC;

f₃=(2с²-a(а-х₃))²/Δr² _BC-((а+х₃)²+y² ₃+4c²-Δr² _BC)/4.

Таким образом, местоположение точки D в системе координат Oxyz определяется системой уравнений

где a₁=(2a/Δr_AB)²-1; b₁=-1; f₁=(Δr_AB/2)²-а².

Система уравнений (3) связывает неизвестные значения координат точки D с известными координатами точек А, В, С и значениями разностей дальностей Δr_AB, Δr_AC и Δr_BC. Однако ввиду наличия функциональной взаимосвязи между входящими в систему уравнениями, данная система имеет бесконечное множество решений. В состав множества решений будут входить векторы координат всех точек пересечения поверхностей положения точки D, описываемых входящими в систему (3) уравнениями.

Определим вид пространственной линии, содержащей все точки, координаты которых являются корнями системы уравнений (3). Для этого рассмотрим сечение поверхностей положения точки D плоскостью, описываемой уравнением z=z_S=const (см. фиг.6).

Для произвольного значения z_S можно записать

где f'_i=f_i-z² _S; i=1...3.

Входящие в систему (4) уравнения являются уравнениями гипербол. Таким образом, решить систему уравнений (4) - значит найти координаты точек пересечения трех гипербол, описываемых входящими в систему уравнениями.

С целью нахождения решений системы (4) приведем ее к виду

где l₁=(a₁Δ_bd+Δ_ad)/K; m₁=(a₁Δ_be+Δ_ae)/K; n₁=(a₁Δ_bf+Δ_af+f₁1Δ_ab)/K;

l₂=-a₁Δ_cd/K; m₂=-a₁Δ_ce/K; n₂=-(a₁Δ_cf+f₁Δ_ac)/K;

l₃=-Δ_cd/K; m₃=-Δ_ce/K; n₃=(-Δ_cf+f₁Δ_bc)/K;

K=a₁Δ_bc+Δ_ac;

Из первого уравнения системы (5) следует, что

y=-(l₁x+n₁)/(x+m₁),

поэтому систему уравнений (5) можно представить в виде

где В₁=l² ₁+2l₂m₁-l₁m₂+n₂;

C₁=2l₁n₁+l₂m₁ ²-m₂n₁-l₁m₁m₂+2m₁n₂;

D₁=n² ₁-m₁m₂n₁+m² ₁n₂;

В₂=m₁+l₃;

С₂=l₃m₁-l₁m₃+n₃;

D₂=m₁n₃-m₃n₁.

Решениями квадратного уравнения системы (6) являются два значения переменной х, определяемые общеизвестными выражениями:

где a, b, c - коэффициенты квадратного уравнения, для данного конкретного случая равные:

Если ввести обозначения

y₁=-(l₁x₁+n₁)/(x₁+m₁) и y₂=-(l₁x₂+n₁)/(x₂+m₁),

то частное разности y₂ и y₁ и разности корней квадратного уравнения х₂ и x₁ определяется выражением

а суммы этих величин - выражениями:

где

Полученный результат может быть интерпретирован следующим образом: поскольку значение отношения (7) не зависит от значения переменной z, следовательно, с учетом (8), все точки, координаты которых являются решениями системы уравнений (3), лежат в одной плоскости, перпендикулярной плоскости хОу, пересекающей ось Ох под углом

и проходящей через точку F с координатами

Полученный результат означает, что два значения разностей дальностей от двух пар опорных точек до искомой точки расположения ИРИ определяют направление (угол азимута γ) на источник радиоизлучения, расположенный на произвольной высоте h над плоскостью ABC (см. фиг.1).

Таким образом, значение угла γ азимута ИРИ вычисляется с использованием выражения

Координаты {x_f, y_f} точки F, принадлежащей линии пеленга ИРИ, вычисляются с использованием выражений:

где

Трем вычисленным значениям (γ, x_f, у_f) соответствует плоскость Ω, проходящая через точку F под углом γ к оси Ох и перпендикулярная плоскости ABC. Поскольку точка D принадлежит одновременно плоскости Ω и поверхности положения, описываемой уравнением (1), следовательно, она принадлежит линии пересечения этих поверхностей (см. фиг.7).

Если ввести в рассмотрение систему координат Ex''y''z'', начало которой совпадает с точкой пересечения плоскости Ω с осью Ox, ∠xEx''=∠γ, (см. фиг.8), то уравнение поверхности положения, описываемой уравнением (1), в данной системе координат имеет вид

где

Поскольку плоскость Ω совпадает с плоскостью x''Ez'', то уравнение гиперболы, являющейся линией пересечения плоскости Ω и поверхности положения, описываемой уравнением (9), получается путем приравнивания у''=0 и имеет вид (см. фиг.9)

Преобразуя уравнение (10), получим

где

m=a₁ ²l²+b²2x₀ ²cos²γ-l²x₀ ²;

x''₀=-b₁ ²x₀cosγ/l².

Поскольку гипербола, описываемая каноническим уравнением вида

асимптотически стремится к прямой (асимптоте) [8], описываемой уравнением

следовательно, за угол места ИРИ можно принять угол наклона асимптоты гиперболы в плоскости х''Ez'' (см. фиг.10), значение которого вычисляется по формуле

Вычисленные значения γ, β с выхода блока анализа поступают в блок индикации, который предназначен для визуализации результатов предлагаемого способа пеленгования.

Таким образом, предлагаемый способ пеленгования, по сравнению с прототипом, обеспечивает возможность определения угла места ИРИ.

ЛИТЕРАТУРА

1. Шебшаевич B.C. Введение в теорию космической навигации. М.: Сов. радио, 1971. - 296 с.

2. Дулевич В.Е., Коростелев А.А., Мельник Ю.А. и др. Теоретические основы радиолокации. / Под ред. В.Е.Дулевича. - М.: Сов. радио, 1964. - 732 с.

3. Теоретические основы радиолокации. Учебное пособие для вузов. / Под ред. Я.Д.Ширмана. - М.: Сов. радио, 1970. - 560 с.

4. Финкельштейн М.И. Основы радиолокации. - М.: Сов. радио, 1973. - 496 с.

5. Белоцерковский Г.Б. Основы радиолокации и радиолокационные устройства. - М.: Сов. радио, 1975. - 336 с.

6. Клименко Н.Н., Клименко С.В. Современное состояние теории и практики радиоинтерферометрии // Зарубежная радиоэлектроника, 1990, N1. - С.3-14.

7. Международная космическая радиотехническая система обнаружения терпящих бедствие. / Под ред. В.С.Шебшаевича. - М.: Радио и связь, 1987. - 376 с.

8. Корн Г., Корн М. Справочник по математике для научных работников и инженеров. - М.: Наука, 1984. - 832 с.

9. Wuu Chenn, Pearson Allan E. On time deley estimation involving received signals // IEEE Trans. Acount., Speech, and Signal Process., 1984, 32, N4, C.828-835.

10. Радиопеленгационная система, использующая круглую антенную решетку. Пат. 4633257, США.

11. Пеленгатор: А.с. 1555695 СССР, МКИ⁵ G 01 S 3/46 / Дикарев В.И., Провоторов Г.Ф., Шерстобитов В.В.

12. Активная радиоинтерференционная система. Пат. 57-51632, Япония.

13. Интерферометр. Пат. 290308, ГДР.

14. Способ и аппаратура для пеленгации и частотной идентификации. Пат. 4443801, США.

15. Одноточечная система определения местоположения. Пат. 4819053, США.

16. Способ определения местоположения передатчика путем измерения разности времен задержек. Пат. 274102, ГДР.

17. Метод гиперболического определения места и устройство для его реализации. Пат. 229866, ГДР.

18. Радиопеленгатор. Пат. 57-51910, Япония.

19. Пеленгование источника радиоизлучений с помощью адаптивной антенной решетки. Пат. 4862180, США.

20. Сайбель А.Г. РДМ способ пеленгования ИРИ и реализующее его устройство. Патент РФ №2258242 от 31.05.2005.

Способ пеленгования источника радиоизлучения (ИРИ), основанный на приеме его сигнала тремя антеннами, измерении разности времен приема сигнала ИРИ антеннами, образующими две измерительные базы, вычислении значений разностей дальностей от ИРИ до антенн, образующих измерительные базы, вычислении значения угла азимута ИРИ, вычислении значений координат точки, принадлежащей линии положения ИРИ, и отображении полученных результатов, отличающийся тем, что вычисляют значение угла места ИРИ с использованием выражения

где α₁=Δr_АВ/2, γ - значение угла азимута ИРИ, Δr_AB - разность расстояний от точки расположения ИРИ до точек А и В расположения соответствующих антенн.