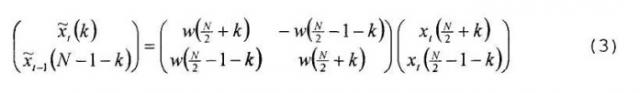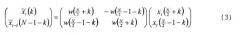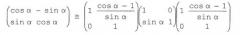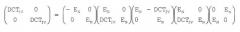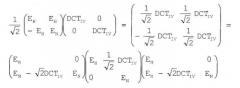Устройство и способ обработки сигнала, имеющего последовательность дискретных значений

Устройство и способ обработки сигнала, имеющего последовательность дискретных значений

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к обработке сигнала и, в частности, к обработке сигнала в виде последовательных значений, например выборок аудиосигнала или выборок видеосигнала, которые, в частности, особенно пригодны для приложений кодирования без потерь.

Настоящее изобретение также применимо к алгоритмам сжатия для дискретных значений, содержащих аудиоинформацию и/или информацию изображения, и, в частности, для алгоритмов кодирования, включающих в себя преобразование в частотной области, или временной области, или пространственной области, предшествующее кодированию, например энтропийному кодированию по методу Хаффмана или арифметическому кодированию.

Современные методы аудиокодирования, например MPEG Layer3 (МР3) или MPEG AAC, используют преобразования, например так называемое модифицированное дискретное косинусное преобразование (MDCT), для получения блочного частотного представления аудиосигнала. Такой аудиокодер обычно получает поток выборок аудиосигнала с дискретизацией по времени. Поток выборок аудиосигнала подвергается вырезанию для получения вырезанного блока, например, из 1,024 или 2,048 вырезанных выборок аудиосигнала. Для вырезания применяются различные вырезающие функции, например синусоидальная вырезающая функция и т.д.

Вырезанные выборки аудиосигнала с дискретизацией по времени преобразуются к спектральному представлению посредством гребенки фильтров. В принципе, для этого можно применять преобразование Фурье или, в особых случаях, разновидность преобразования Фурье, например FFT, или рассматриваемое MDCT. Блок спектральных значений аудиосигнала на выходе гребенки фильтров можно, при необходимости, дополнительно обрабатывать. В вышеописанных аудиокодерах затем обычно производится квантование спектральных значений аудиосигнала, причем стадии квантования обычно выбирают так, чтобы шум квантования, обусловленный квантованием, был ниже порога психоакустической маскировки, т.е. был «вырезан с помощью маски». Квантование является кодированием с потерями. Для получения дополнительного сокращения объема данных квантованные спектральные значения подвергают энтропийному кодированию, например, посредством кодирования по Хаффману. Мультиплексор битового потока формирует из энтропийно-кодированных квантованных спектральных значений битовый поток, который можно сохранять или передавать, путем добавления дополнительной информации, например масштабных коэффициентов и т.д.

В аудиодекодере битовый поток разделяется на кодированные квантованные спектральные значения и дополнительную информацию посредством демультиплексора битового потока. Энтропийно-кодированные квантованные спектральные значения сначала подвергаются энтропийному декодированию для получения квантованных спектральных значений. Затем квантованные спектральные значения подвергаются обратному квантованию для получения декодированных спектральных значений, содержащих шум квантования, который, однако, ниже порога психоакустической маскировки и потому не слышен. Эти спектральные значения затем преобразуются к временному представлению посредством синтезирующей гребенки фильтров для получения декодированных выборок аудиосигнала с дискретизацией по времени. В синтезирующей гребенке фильтров должен применяться алгоритм преобразования, обратный к упомянутому алгоритму преобразования. Кроме того, вырезание должно быть обращено после обратного преобразования частота-время.

Для достижения хорошей частотной избирательности современные аудиокодеры обычно используют перекрытие блоков. Такой случай показан на фиг. 6A. Сначала берут, например, 2,048 выборок аудиосигнала с дискретизацией по времени и обрезают посредством средства 402. Средство 402 реализации окна обрезки имеет длину окна 2N выборок и обеспечивает блок из 2N вырезанных выборок на выходной стороне. Для достижения перекрытия окон второй блок из 2N вырезанных выборок формируется посредством средства 404, которое показано отдельно от средства 402 на фиг. 6A только для ясности. Однако 2,048 выборок, поступающих на средство 404, не являются выборками аудиосигнала с дискретизацией по времени, непосредственно следующими за первым окном, но содержат вторую половину выборок, вырезанных средством 402, и дополнительно содержат только 1,024 «новых» выборок. Перекрытие символически показано на фиг. 6A как средство 406, обеспечивающее степень перекрытия 50%. 2N вырезанных выборок, выводимые средством 402, и 2N вырезанных выборок, выводимые средством 404, затем обрабатываются согласно алгоритму MDCT посредством средств 408 и 410 соответственно. Средство 408 обеспечивает N спектральных значений для первого окна согласно известному алгоритму MDCT, а средство 410 также обеспечивает N спектральных значений, но для второго окна, причем между первым окном и вторым окном существует перекрытие 50%.

В декодере N спектральных значений первого окна, показанные на фиг. 6B, поступают на средство 412, осуществляющее обратное модифицированное дискретное косинусное преобразование. То же самое происходит с N спектральными значениями второго окна. Они поступают на средство 414, также осуществляющее обратное модифицированное дискретное косинусное преобразование. Каждое из средств 412 и 414 обеспечивают 2N выборок для первого окна и 2N выборок для второго окна соответственно.

На средстве 416, обозначенном TDAC (отмена перекрытия во временной области) на фиг. 6B, учитывается тот факт, что два окна перекрываются. В частности, выборка y₁ второй половины первого окна, т.е. с индексом N+k, суммируется с выборкой y₂ из первой половины второго окна, т.е. с индексом k, так что на выходной стороне, т.е. на декодере, получается N декодированных временных выборок.

Заметим, что посредством функции средства 416, которая также называется функцией сложения, вырезание, осуществляемое на кодере, схематически изображенном на фиг. 6A, учитывается в каком-то роде автоматически, поэтому на декодере, показанном на фиг. 6B, не требуется никакого явного «обратного (обращенного) вырезания».

Если вырезающую функцию, реализуемую средством 402 или 404, обозначить w(k), где индекс k представляет индекс времени, должно выполняться условие, состоящее в том, что вырезающий весовой коэффициент w(k) в квадрате плюс вырезающий весовой коэффициент w(N+k) в квадрате равно 1, где k принимает значения от 0 до N-1. Если используется синусоидальная вырезающая функция, в которой вырезающие весовые коэффициенты выражаются первой полуволной синусоидальной функции, это условие всегда выполняется, поскольку квадрат синуса плюс квадрат косинуса равно 1 для любого угла.

Метод вырезания с последующим применением функции MDCT, описанный на фиг. 6A, страдает тем недостатком, что вырезание путем умножения выборки с дискретизацией по времени, с использованием синусоидальной вырезающей функции, осуществляется посредством числа с плавающей точкой, поскольку синус угла от 0 до 180 градусов не дает целое число, за исключением угла 90 градусов. Даже при вырезании целочисленных выборок с дискретизацией по времени после вырезания получаются числа с плавающей точкой.

Поэтому, даже если не используется психоакустический кодер, т.е. необходимо обеспечить кодирование без потерь, на выходе средств 408 и 410 соответственно необходимо квантование, чтобы можно было осуществлять разумно управляемое энтропийное кодирование.

В общем случае, известные в настоящее время целочисленные преобразования для аудио- и/или видеокодирования без потерь получаются путем разложения используемых в нем преобразований на повороты Гивенса и применения схемы поднятия к каждому повороту Гивенса. При этом на каждом этапе вносится ошибка округления. Для последующих стадий поворотов Гивенса ошибка округления продолжает накапливаться. Результирующая ошибка аппроксимации создает проблемы, в частности, для подходов аудиокодирование без потерь, в частности, когда используются длинные преобразования, обеспечивающие, например, 1,024 спектральных значений, например, это происходит в известном MDCT с перекрытием и сложением (MDCT = модифицированное дискретное косинусное преобразование). В частности, в более высоком частотном диапазоне, где аудиосигнал обычно имеет очень низкую энергию, ошибка аппроксимации может быстро превысить фактический сигнал, поэтому эти подходы создают проблемы в отношении кодирования без потерь и, в частности, в отношении эффективности кодирования, которой при этом можно добиться.

В отношении аудиокодирования целочисленные преобразования, т.е. алгоритмы преобразования, генерирующие целые выходные значения, в частности, основаны на известном DCT-IV, которое не учитывает компонент DC, тогда как целочисленные преобразования для приложений обработки изображений, напротив, основаны на DCT-II, которое особо содержит обеспечения для компонента DC. Такие целочисленные преобразования, например, известны из Y. Zeng, G. Bi и Z. Lin, "Integer sinusoidal transforms based on lifting factorization", в Proc. ICASSP'01, май 2001, стр. 1,181 - 1,184, K. Komatsu и K. Sezaki, "Reversible Discrete Cosine Transform", в Proc. ICASSP, 1998, т. 3, стр. 1,769 - 1,772, P. Hao и Q. Shi, "Matrix factorizations for reversible integer mapping", IEEE Trans. Signal Processing, Signal Processing, т. 49, стр. 2,314 -2,324, и J. Wang, J. Sun и S. Yu, "1-d и 2-d transforms from integers to integers", в Proc. ICASSP'03, Hong Kong, апрель 2003.

Как отмечено выше, описанные здесь целочисленные преобразования основаны на разложении преобразования на повороты Гивенса и на применении известной схемы поднятия к поворотам Гивенса, что создает проблему накопления ошибок округления. Это, в частности, обусловлено тем фактом, что в преобразовании округления должны осуществляться много раз, т.е. после каждого этапа поднятия, поэтому, в частности, в длинных преобразованиях, обуславливающих соответственно большое число этапов поднятия, должно быть особенно большое число округлений. Согласно описанному это приводит к накоплению ошибки и, в частности, также к относительному усложнению обработки, поскольку округление осуществляется после каждого этапа поднятия для осуществления следующего этапа поднятия.

Впоследствии разложение вырезания MDCT будет вновь описано со ссылкой на фиг. 9-11 согласно описанному в DE 10129240 A1, где это разложение вырезания MDCT на повороты Гивенса с помощью матриц поднятия и соответствующими округлениями преимущественно совместимо с концепцией, рассмотренной согласно фиг. 1 для преобразования и согласно фиг. 2 для обратного преобразования, для получения полностью целочисленной аппроксимации MDCT, т.е. целочисленного MDCT (Int-MDCT) согласно настоящему изобретению, в котором концепция прямого и обратного преобразования проиллюстрированы на примере MDCT.

На фиг. 3 показана общая схема предпочтительного устройства изобретения для обработки выборок с дискретизацией по времени, представляющей аудиосигнал для получения целых значений, на основании которых может работать алгоритм целочисленного преобразования Int-MDCT. Выборки с дискретизацией по времени вырезаются устройством, показанным на фиг. 3, и, в необязательном порядке, преобразуются к спектральному представлению. Выборки с дискретизацией по времени, поступающие на устройство на входе 10, вырезаются с помощью окна w, длина которого соответствует 2N выборкам с дискретизацией по времени, для получения на выходе 12 целочисленных вырезанных выборок, пригодных для преобразования к спектральному представлению посредством преобразования и, в частности, средством 14 для осуществления целочисленного DCT. Целочисленное DCT предназначено для генерации N выходных значений из N входных значений, в чем состоит отличие от функции MDCT 408, показанной на фиг. 6A, которая генерирует только N спектральных значений из 2N вырезанных выборок согласно уравнению MDCT.

Для вырезания выборок с дискретизацией по времени, средство 16 выбирает первые две выборки с дискретизацией по времени, которые совместно представляют вектор выборок с дискретизацией по времени. Выборка с дискретизацией по времени, выбранная средством 16, является первой четвертью окна. Другая выборка с дискретизацией по времени является второй четвертью окна, что описано более подробно со ссылкой на фиг. 5. Вектор, генерируемый средством 16, можно представить матрицей вращения размером 2x2, в которой эта операция осуществляется не напрямую, а посредством нескольких так называемых матриц поднятия.

Свойство матрицы поднятия состоит в том, что она содержит только один элемент, зависящий от окна w и не равный "1" или "0".

Разложение преобразований элементарной волны на этапах поднятия представлено в публикации для специалистов "Factoring Wavelet Transforms Into Lifting Steps", Ingrid Daubechies and Wim Sweldens, Preprint, Bell Laboratories, Lucent Technologies, 1996. В общем случае, схема поднятия является простым отношением между парами фильтров с хорошим восстановлением, имеющими одинаковые низкочастотные или высокочастотные фильтры. Каждую пару комплементарных фильтров можно разложить на этапы поднятия. Это применимо, в частности, к поворотам Гивенса. Рассмотрим случай, когда многофазная матрица является поворотом Гивенса. Затем применяется следующее:

Каждая из трех матриц поднятия в правой стороне с одинаковым знаком имеет значение "1" в качестве элемента главной диагонали. Кроме того, в каждой матрице поднятия элемент второй диагонали равен нулю и элемент второй диагонали зависит от угла поворота α.

Вектор умножается на третью матрицу поднятия, т.е. матрицу поднятия, находящуюся в самом правом положении в вышеприведенном уравнении, для получения первого результирующего вектора. Это проиллюстрировано на фиг. 3 средством 18. После этого первый результирующий вектор округляется любой функцией округления, отображающей множество действительных чисел в множество целых чисел, что проиллюстрировано на фиг. 3 средством 20. На выходе средства 20 получается первый результирующий вектор. Округленный первый результирующий вектор поступает на средство 22 для умножения на среднюю, т.е. вторую матрицу поднятия для получения второго результирующего вектора, который снова округляется средством 24 для получения округленного второго результирующего вектора. Затем округленный второй результирующий вектор поступает на средство 26 для умножения на матрицу поднятия, показанную слева в вышеприведенном уравнении, т.е. первую матрицу, для получения третьего результирующего вектора, который окончательно округляется посредством средства 28 для окончательного получения целочисленных вырезанных выборок на выходе 12, которые, если нужно их спектральное представление, должны обрабатываться средством 14 для получения целочисленных спектральных значений на спектральном выходе 30.

Предпочтительно средство 14 реализовано как целочисленное DCT.

Дискретное косинусное преобразование 4-го типа (DCT-IV) с длиной N задается следующим уравнением:

Коэффициенты DCT-IV образуют ортонормальную матрицу N x N. Каждую ортогональную матрицу N x N можно разложить на N (N-1)/2 поворотов Гивенса, как описано в публикации для специалистов P. P. Vaidyanathan, "Multirate Systems And Filter Banks", Prentice Hall, Englewood Cliffs, 1993. Заметим, что существуют и другие разложения.

В отношении других классификаций различных алгоритмов DCT, см. H. S. Malvar, "Signal Processing With Lapped Transforms", Artech House, 1992. В общем случае, алгоритмы DCT отличаются родом своих базисных функций. Хотя предпочтительное здесь DCT-IV включает в себя несимметричные базисные функции, т.е. четвертьволна косинуса, 3/4 волны косинуса, 5/4 волны косинуса, 7/4 волны косинуса и т.д., дискретное косинусное преобразование, например, типа II (DCT-II) имеет осесимметричные и центральносимметричные базисные функции. 0-я базисная функция имеет компонент DC, первая базисная функция имеет половину волны косинуса, вторая базисная функция имеет целую волну косинуса и т.д. В силу того что DCT-II делает особый упор на компонент DC, оно используется в видеокодировании, но не в аудиокодировании, поскольку компонент DC не относится к аудиокодированию, в отличие от видеокодирования.

Ниже будет описано, как угол поворота α для поворота Гивенса зависит от вырезающей функции.

MDCT с длиной окна 2N можно свести к дискретному косинусному преобразованию типа IV длиной N. Для этого в явном виде осуществляется операция TDAC во временной области, после чего применяется DCT-IV. В случае 50% перекрытия левая половина окна для блока t перекрывается с правой половиной предыдущего блока, т.е. блока t-1. Область перекрытия двух последовательных блоков t-1 и t предварительно обрабатывается во временной области, т.е. до преобразования, следующим образом, т.е. обрабатывается между входом 10 и выходом 12 на фиг. 3:

Значения, помеченные тильдой, это значения на выходе 12 на фиг. 3, тогда как значения х, не помеченные тильдой в вышеприведенном уравнении, это значения на входе 10 и/или следующие за средством 16 для выбора. Переменный индекс k принимает значения от 0 до N/2-1, а w представляет вырезающую функцию.

Из условия TDAC для вырезающей функции w, следует:

Для определенных углов α_k, k = 0,..., N/2-1, эту предварительную обработку во временной области можно записать как поворот Гивенса, как рассмотрено.

Угол α поворота Гивенса зависит от вырезающей функции w следующим образом:

α = arctan[w(N/2-1-k) / w(N/2 + k)] (5)

Заметим, что любую вырезающую функцию w можно использовать, пока она удовлетворяет этому условию TDAC.

Ниже, со ссылкой на фиг. 4, описаны каскадные кодер и декодер. Выборки с дискретизацией по времени с x(0) по x(2N-1), которые совместно «вырезаются» окном, сначала выбираются средством 16 на фиг. 3, так что выборка x(0) и выборка x(N-1), т.е. выборка из первой четверти окна и выборка из второй четверти окна, выбираются для формирования вектора на выходе средства 16. Пересекающиеся стрелки схематически представляют умножения с поднятием и последующие округления, выполняемые средствами 18, 20 и 22, 24 и 26, 28, соответственно, для получения целочисленных вырезанных выборок на входе блоков DCT-IV.

После обработки первого вектора согласно описанному выше, второй вектор дополнительно выбирается из выборок x(N/2-1) и x(N/2), т.е., опять же, выборки из первой четверти окна и выборки из второй четверти окна, и, опять же, обрабатывается алгоритмом, описанным на фиг. 3. Аналогично обрабатываются все остальные пары выборок из первой и второй четвертей окна. Такая же обработка применяется для третьей и четвертой четвертей первого окна. Теперь существует 2N целочисленных вырезанных выборок на выходе 12, которые поступают на преобразование DCT-IV, что проиллюстрировано на фиг. 4. В частности, целочисленные вырезанные выборки второй и третьей четвертей поступают на DCT. Целочисленные вырезанные выборки первой четверти окна обрабатываются в предыдущее DCT-IV совместно с целочисленными вырезанными выборками четвертой четверти предыдущего окна. Аналогично, согласно фиг. 4, четвертая четверть целочисленных вырезанных выборок поступает на преобразование DCT-IV совместно с первой четвертью следующего окна. Среднее целочисленное преобразование 32 DCT-IV, показанное на фиг. 4 обеспечивает N целых спектральных значений с y(0) по y(N-1). Затем эти целые спектральные значения можно, например, просто подвергать энтропийному кодированию без необходимости вставлять квантование, поскольку вырезание и преобразование дают целые выходные значения.

В правой части фиг. 4 показан декодер. Декодер, состоящий из обратного преобразования и «обратного вырезания», действует обратно кодеру. Показано, что обратное DCT-IV можно использовать для обратного преобразования DCT-IV, показанного на фиг. 4. Выходные значения декодера DCT-IV 34 подвергаются обратному преобразованию с соответствующими значениями предыдущего преобразования и/или последующего преобразования, как показано на фиг. 4, для повторной генерации выборок аудиосигнала с дискретизацией по времени с x(0) по x(2-N1) из целочисленных вырезанных выборок на выходе средства 34 и/или предыдущего и последующего преобразования.

Операция на выходной стороне осуществляется посредством обратного поворота Гивенса, т.е. при этом блоки 26, 28 и 22, 24 и 18, 20, соответственно, проходят в противоположном направлении. Это будет проиллюстрировано более подробно применительно ко второй матрице поднятия уравнения 1. Когда (на кодере) второй результирующий вектор формируется путем умножения округленного первого результирующего вектора на вторую матрицу поднятия (средство 22), следующее выражение дает:

Значения x, у в правой стороне уравнения 6 являются целыми. Это, однако, не применяется к значению x sin α. Здесь нужно ввести функцию округления r, проиллюстрированную следующим уравнением:

Эта операция осуществляется средством 24.

Обратное отображение (в декодере) определяется следующим образом:

По причине знака минус перед операцией округления становится очевидно, что целочисленную аппроксимацию этапа поднятия можно обратить, не внося ошибку. Применение этой аппроксимации к каждому из трех этапов поднятия приводит к целочисленной аппроксимации поворота Гивенса. Округленный поворот (на кодере) можно обратить (на декодере), не внося ошибку при прохождении обратных этапов поднятия с округлением в обратном порядке, т.е. при декодировании алгоритма на фиг. 3, осуществленном снизу вверх.

Если функция округления r центральносимметрична, то обратный округленный поворот идентичен округленному повороту на угол -α и выражается следующим образом:

Матрицы поднятия для декодера, т.е. для обратного поворота Гивенса, в этом случае получаются непосредственно из уравнения (1) простой заменой выражения "sin α" выражением "-sin α".

Ниже, разложение общего MDCT с перекрывающимися окнами 40-46 проиллюстрировано со ссылкой на фиг. 5. Каждое из окон 40-46 имеет 50% перекрытие. Сначала повороты Гивенса осуществляются для каждого окна в первой и второй четвертях окна и/или в третьей и четвертой четвертях окна, что схематически показано стрелками 48. Затем повернутые значения, т.е. целочисленные вырезанные выборки, поступают на DCT из N в N, так что всегда вторая и третья четверти окна и четвертая и первая четверти последующего окна, соответственно, совместно преобразуются в спектральное представление посредством алгоритма DCT-IV.

Поэтому общие повороты Гивенса разлагаются на матрицы поднятия, которые выполняются последовательно, причем после каждого умножения на матрицу поднятия вставляется этап округления, так что числа с плавающей точкой округляются сразу же после генерации, так что до каждого умножения результирующего вектора на матрицу поднятия результирующий вектор имеет только целые компоненты.

Таким образом, выходные значения всегда остаются целыми, причем предпочтительно использовать также целые входные значения. Это не представляет ограничения, поскольку любые иллюстративные выборки PCM, сохраняемые на CD, являются целочисленными значениями, диапазон которых варьируется в зависимости от битовой ширины, т.е. в зависимости от того, являются ли цифровые входные значения с дискретизацией по времени 16-битовыми значениями или 24-битовыми значениями. Тем не менее, процесс в целом можно обратить, как рассмотрено выше, осуществляя обратные повороты в обратном порядке. Таким образом, это целочисленная аппроксимация MDCT с хорошим восстановлением, т.е. преобразование без потерь.

Показанное преобразование обеспечивает целые выходные значения, а не значения с плавающей точкой. Это обеспечивает хорошее восстановление, т.е. при осуществлении прямого, а затем обратного преобразования не вносится никаких ошибок. Согласно предпочтительному варианту осуществления настоящего изобретения преобразование является заменой для модифицированного дискретного косинусного преобразования. Однако, пока возможно разложение на повороты и разложение поворотов на этапы поднятия, можно осуществлять и другие методы преобразования с целыми числами.

Целочисленное MDCT имеет большинство полезных свойств MDCT. Оно имеет структуру перекрытия, благодаря чему достигается более высокая частотная эффективность, чем у преобразований с неперекрывающимися блоками. Поскольку при вырезании до преобразования уже учитывается функция TDAC, поддерживается критическое осуществление выборки, так что полное количество спектральных значений, представляющих аудиосигнал, равно полному количеству входных выборок.

По сравнению с нормальным MDCT, обеспечивающим выборки с плавающей точкой, описанное предпочтительное целочисленное преобразование показывает, что шум по сравнению с нормальным MDCT повышается только в спектральном диапазоне, где имеется низкий уровень сигнала, тогда как при значительных уровнях сигнала это повышение шума не становится заметным. Однако обработка целых чисел предусматривает экономичную аппаратную реализацию, поскольку используются только этапы умножения, которые можно легко разложить на этапы сдвига/сложения, которые допускают простую и быструю аппаратную реализацию. Возможна, конечно, и программная реализация.

Целочисленное преобразование обеспечивает хорошее спектральное представление аудиосигнала и одновременно остается в области целых чисел. В случае применения к тональным частям аудиосигнала, оно дает хорошую концентрацию энергии. При этом можно построить экономичную схему кодирования без потерь, просто каскадируя вырезание/преобразование, показанное на фиг. 3, с энтропийным кодером. В частности, преимуществом обладает стековое кодирование, использующее переходные значения, которое применяется в MPEG AAC. Предпочтительно масштабировать в сторону уменьшения все значения с определенным коэффициентом два, пока они не впишутся в нужную кодовую таблицу, после чего дополнительно кодировать опущенные младшие биты. По сравнению с альтернативным использованием более крупных кодовых таблиц описанная альтернатива более предпочтительна в отношении потребления емкость хранения для хранения кодовых таблиц. Почти беспотерьный кодер также можно получить, просто опуская некоторые единицы в младших битах.

В частности, для тоновых сигналов энтропийное кодирование целых спектральных значений позволяет добиться высокой эффективности кодирования. Для переходных частей сигнала эффективность кодирования низка, конкретно, вследствие плоского спектра переходных сигналов, т.е. вследствие малого количества спектральных значений, равных или почти равных 0. Однако согласно описанному в J. Herre, J. D. Johnston: "Enhancing the Performance of Perceptual Audio Coders by Using Temporal Noise Shaping (TNS)" 101^st AES Convention, Los Angeles, 1996, препринт 4384, эту плоскостность можно использовать, применяя линейное прогнозирование в частотной области. Альтернативой является прогнозирование с открытым циклом. Другой альтернативой является прогнозирование с замкнутым циклом. Первая альтернатива, т.е. прогнозирование с открытым циклом, называется TNS. Квантование после прогнозирования обеспечивает адаптацию результирующего шума квантования к временной структуре аудиосигнала и, таким образом, предотвращает предварительные эхо в психоакустических аудиокодерах. Для аудиокодирования без потерь вторая альтернатива, т.е. прогнозирование с замкнутым циклом, более подходящая, т.к. позволяет точно восстанавливать входной сигнал. В случае применения этого способа к генерируемому спектру этап округления нужно осуществлять после каждого этапа фильтра прогнозирования, чтобы оставаться в области целых чисел. Используя обратный фильтр и ту же функцию округления, можно точно воспроизвести исходный спектр.

Для использования избыточности между двумя каналами для предварительной обработки данных центрально-боковое кодирование также можно применять без потерь, если используется округленный поворот на угол π/4. По сравнению с альтернативой вычисления суммы и разности левого и правого канала стереосигнала округленный поворот имеет преимущество экономии энергии. Использование методов так называемого комбинированного стереокодирования может включаться или выключаться для каждого диапазона, что также осуществляется в стандартном MPEG AAC. Можно также учитывать дополнительные углы поворота, чтобы иметь возможность более гибко снижать избыточность между двумя каналами.

В частности, концепция преобразования, проиллюстрированная в отношении фиг. 3, обеспечивает целочисленную реализацию MDCT, т.е. IntMDCT, которая действует без потерь в отношении прямого преобразования и последующего обратного преобразования. Благодаря этапам округления 20, 24, 28 и соответствующим этапам округления в целочисленном DCT (блок 14 на фиг. 3), также всегда возможна обработка целых чисел, т.е. обработка с более грубо квантованными значениями, чем на момент их генерации, например, путем умножения с плавающей точкой на матрицу поднятия (блоки 18, 22, 26 на фиг. 3).

В результате, все IntMDCT можно эффективно осуществлять в отношении вычисления.

Беспотерьность этого IntMDCT или, в целом, беспотерьность всех алгоритмов кодирования означает, что отсутствие потерь связано с тем, что сигнал, будучи кодирован для получения кодированного сигнала, а затем снова декодирован для получения кодированного/декодированного сигнала, «выглядит» в точности, как исходный сигнал. Другими словами, исходный сигнал идентичен кодированному/декодированному исходному сигналу. Это, очевидно, контрастирует с так называемым кодированием с потерями, в котором, как в случае аудиокодеров, работающих на психоакустической основе, данные безвозвратно теряются вследствие процесса кодирования и, в частности, процесса квантования под управлением психоакустической модели.

Конечно, по-прежнему, вносятся ошибки округления. Таким образом, согласно фиг. 3, в блоках 20, 24, 28 осуществляются этапы округления, которые, конечно, вносят ошибку округления, которая «устраняется» в декодере при осуществлении обратных операций. Таким образом, концепция кодирования/декодирования без потерь существенно отличается от концепций кодирования/декодирования с потерями в том, что в концепциях кодирования/декодирования без потерь ошибка округления вносится так, что ее можно вновь устранить, в отличие от концепций кодирования/декодирования с потерями.

Однако если рассматривать кодированный сигнал, т.е. в примере кодеров с преобразованием, спектр блока временных выборок, округление при прямом преобразовании и/или, в целом, квантование такого сигнала приводит к внесению ошибки в сигнал. Таким образом, ошибка округления "накладывается" на идеальный, свободный от ошибок спектр сигнала, причем ошибка обычно, например в случае фиг. 3, представляет собой белый шум, в равной степени включающий в себя все частотные компоненты рассматриваемого спектрального диапазона. Этот белый шум, наложенный на идеальный спектр, представляет, таким образом, ошибку округления, которая имеет место, например, при округлении в блоках 20, 24, 28 в ходе вырезания, т.е. в ходе предварительной обработки сигнала до фактического DCT в блоке 14. В частности, отметим, что при необходимости отсутствия потерь вся ошибка округления непременно должна кодироваться, т.е. передаваться на декодер, поскольку декодер требует всю ошибку округления, внесенную в кодере, для достижения точного восстановления без потерь.

Ошибка округления может не представлять проблемы, когда со спектральным представлением «ничего не делается», т.е. когда спектральное представление только сохраняется, передается и декодируется, опять же, точно согласованным обратным декодером. В этом случае, критерий отсутствия потерь всегда будет выполняться, независимо от того, насколько большая ошибка округления была внесена в спектр. Если же со спектральным представлением что-то делается, т.е. с идеальным спектральным представлением исходного сигнала, содержащим ошибку округления, например, если генерируются уровни масштабирования и т.д., все это работает тем лучше, чем меньше ошибка округления.

Таким образом, для кодирования/декодирования без потерь требуется, с одной стороны, чтобы сигнал был восстанавливаемым без потерь специальными декодерами, но, с другой стороны, чтобы сигнал имел минимальную ошибку округления в своем спектральном представлении для сохранения гибкости в том, что спектральное представление можно также подавать на неидеально беспотерьные декодеры или что можно генерировать уровни масштабирования и т.д.

Согласно рассмотренному выше ошибка округления выражается как белый шум на всем рассматриваемом спектре. С другой стороны, в частности, в приложениях высокого качества, поскольку для них особенно важно отсутствие потерь, т.е. в аудиоприложениях с очень высокими частотами дискретизации, например 96 кГц, аудиосигнал имеет сигнал осмысленного содержания только в некотором спектральном диапазоне, который обычно достигает, самое большее, 20 кГц. Обычно диапазон, в котором в основном сконцентрирована энергия сигнала для аудиосигнала, заключен от 0 до 10 кГц, тогда как в диапазоне свыше 10 кГц энергия сигнала будет значительно снижаться. Однако это не относится к белому шуму, внесенному округлением. Он накладывается на весь рассматриваемый спектральный диапазон энергии сигнала. В результате, в спектральных диапазонах, т.е. обычно в верхних спектральных диапазонах, где нет энергии аудиосигнала или она очень мала, будет присутствовать только ошибка округления. В то же время, в частности, вследствие ее недерминистического характера ошибку округления также трудно кодировать, т.е. она кодируется только с относительно высокими битовыми требованиями. Битовые требования не играют решающей роли, в частности, в некоторых беспотерьных приложениях. Однако, чтобы приложения кодирования без потерь получали все более широкое распространение, очень важно, чтобы они работали с высокой битовой эффективностью для объединения преимущества отсутствия снижения качества, свойственного беспотерьным приложениям с соответствующей битовой эффективностью, которая известна из концепций кодирования с потерями.

Задачей настоящего изобретения является обеспечение эффективного принципа обработки сигналов.

Эта задача решается посредством устройства для обработки сигнала, имеющего последовательность дискретных значений, по п.1, способа обработки сигнала, имеющего последовательность дискретных значений, по п.18 или компьютерной программы по п.19.

В основе настоящего изобретения лежит тот факт, что, в частности, в контексте кодирования/декодирования без потерь, спектрально ошибка округления формируется так, что она «размещается» в частотном диапазоне сигнала, подлежащего кодированию, в котором сигнал имеет высокую энергию сигнала, и что вследствие этого ошибка округления отсутствует в диапазонах, где сигнал не имеет энергии. В то время как согласно предшествующему уровню техники ошибка округления распределяется белым шумом по всему спектру сигнала при кодировании без потерь и, в частности, при кодировании без потерь на основании целочисленных алгоритмов согласно изобретению ошибка округления накладывается на идеальный спектр в форме розового шума, т.е. так, что энергия шума, обусловленная округлением, присутствует там, где сигнал имеет свою наивысшую энергию сигнала, и, таким образом, так, что шум, обусловленный ошибкой округления, также имеет малую или даже нулевую энергию там, где сигнал, подлежащий кодированию, сам не имеет энергии. Это позволяет избежать наихудшего случая, когда ошибка округления, которую трудно кодировать по причине ее стохастического характера, является единственным сигналом, подлежащим кодированию в частотном диапазоне, из-за чего без необходимости повышается расход битов.

В отношении аудиосигнала, энергия которого находится в нижнем частотном диапазоне, средство округления согласно изобретению выполнено с возможностью формировать низкочастотный спектр генерируемой ошибки округления, вследствие чего на высоких частотах кодированного сигнала нет ни энергии сигнала, ни энергии шума, в то время как ошибка округления отображается в диапазон, где сигнал имеет большую энергию.

В частности, для приложени