Способ исследования структурно-динамических свойств вещества

Способ исследования структурно-динамических свойств вещества

Иллюстрации

Показать все

Реферат

Изобретение относится к неразрушающим методам исследования структурно-динамических свойств вещества, а именно к области анализа атомных и молекулярных движений (колебания, диффузия, релаксация) в реальном времени на наноскопических масштабах с помощью неупругого рассеяния нейтронов. Микроскопическая динамика в значительной степени определяет комплекс макроскопических физических свойств вещества, таких как теплоемкость и теплопроводность, электромагнитные, акустические, вязкоупругие и прочностные свойства. Знание динамики создает фундаментальную основу для понимания физических свойств конденсированных сред, что в особенности актуально и значимо при анализе динамики с высоким энергетическим разрешением (до 10^-9 эВ) на временах 10^-12-10^-8 c для решения проблем физики, химии и технологии наноструктур (макромолекулы, коллоидные частицы, атомные и молекулярные кластеры - фуллерены, нанострубы). Указанные объекты служат элементами функциональных материалов в электронике, лазерной оптике, микромеханике, биохимии и фармацевтике и молекулярной медицине. В связи с этим крайне необходимо осуществлять аттестацию и контроль, прогнозировать поведение указанных объектов прямыми микроскопическими методами, что и обеспечивает предлагаемый способ.

Подчеркнем, что в отличие от квантовых объектов атомного уровня нанообъекты и структуры, как правило, являются квазиклассическими. Для адекватного описания динамики на уровне наноструктуры анализ частотных спектров возбуждений этих систем оказывается недостаточным, требуется изучение их поведения в реальном пространстве и времени, что диктует необходимость развития нейтронных Фурье-методов, обеспечивающих уникальную информацию, недоступную известным методам.

Известен Фурье-способ исследования структуры вещества с помощью малоуглового рассеяния нейтронов, описанный в А.С. №1673934 [1]. Способ основан на том, что на исследуемый образец направляют монохроматический сфокусированный пучок нейтронов, промодулированный по интенсивности с помощью решетки (Фурье-фильтра) с периодической функцией пропускания, установленной перпендикулярно к оси пучка. Производят анализ рассеянного пучка с помощью второй решетки с периодической функцией пропускания, сдвинутой на половину периода относительно функции пропускания первой решетки и установленной симметрично относительно образца и первой решетки. Далее производят линейные перемещения по оси пучка и угловые перемещения решеток в собственных плоскостях, сохраняя симметрию их расположения относительно образца и сдвиг их функций пропускания. Затем измеряют интенсивность рассеянного пучка при каждом линейном и угловом положениях решеток. На основе измеренных интенсивностей определяют статическую корреляционную функцию рассеяния образца, по которой судят о его структуре.

Данный Фурье-метод действительно характеризует структуру образца в реальном пространстве, однако не позволяет получить информацию об атомной динамике вещества.

Известен Фурье-метод исследования структурно-динамических свойств вещества, описанный в работе [2]. Способ заключается в том, что Фурье-фильтры, описанные в [1], используются для модуляции спектра нейтронов по энергии (длине волны) и анализа энергии нейтрона после рассеяния в образце, что позволяет измерять корреляционную функцию изучаемого объекта, характеризующую его поведение во времени. Результат достигается тем, что Фурье-фильтры, установленные эквидистантно до и после образца, приводятся в движение в направлении, поперечном пучку. Вариация скорости движения служит для сканирования диапазона времени 10^-12-10^-8 с, в котором проявлена динамика образца на наноскопическом уровне.

Недостатком данного метода является его низкая светосила. Потери потока нейтронов при модуляции исходного пучка и энергетическом анализе рассеянных нейтронов достигают 90%. Другой недостаток метода заключается в том, что он дает неполную информацию о структурно-динамических свойствах вещества, измеряя только косинус-Фурье-преобразование частотного спектра объекта. Данные, предоставляемые этим методом, отражают только четную по частоте часть спектра возбуждений образца, а нечетная часть спектра вообще не учитывается.

Наиболее близким по технической сущности к заявляемому объекту является способ исследования структурно-динамических свойств вещества с помощью неупругого рассеяния нейтронов, описанный в [3]. Способ [3], называемый нейтронное спин-эхо (neutron spin-echo, NSE) и направленный на исследование динамики наноскопических систем в реальном времени, заключается в следующем. Монохроматизированный пучок поляризованных нейтронов последовательно проходит через две области магнитного поля. Первоначально при отсутствии образца вектор поляризации нейтронов совершает одинаковое число прецессий вокруг направления каждого из полей. Затем между областями поля устанавливают образец. В результате неупругого рассеяния в образце скорость и длина волны нейтронов становятся отличными от исходных величин. В итоге число прецессий вектора поляризации во втором поле отличается от такого в первом, а разность числа прецессий показывает наличие неупругого рассеяния. В способе-прототипе измеряют косинус-Фурье-образ интегральной по энергетическому спектру нейтронов поляризации, по которой судят о динамике образца, связанной с четной частью его частотного спектра возбуждений. Способ-прототип обладает высокой светосилой и разрешением, позволяя изучать структурно-динамические свойства вещества в диапазоне времени 10^-12-10^-8 c.

Однако существенным недостатком способа-прототипа является то, что в нем анализируется только четная часть S_even=[S(ω,q)+S(-ω,q)]/2 частотного спектра образца S(ω,q), так как способ позволяет определить лишь косинус-Фурье-преобразование частотного спектра изучаемого объекта S_even(t,q,)˜, где t - время, ω - частота, q - импульс, переданный нейтрону при рассеянии в образце. Возможности способа-прототипа ограничены измерением четной части спектра S_even, a нечетная часть спектра S_odd=[S(ω,q)-S(-ω,q)]/2 вообще не анализируется в силу того, что она в экспериментальных данных не выявляется. Тем самым теряется существенная информация о динамике объекта и его взаимодействии с нейтроном в процессах рассеяния, при которых в среднем энергия нейтрона возрастает или уменьшается, что отражено в нечетной части спектра возбуждений образца.

Задачей заявляемого изобретения является обеспечение полного анализа структурно-динамических свойств вещества путем получения всего объема данных о спектре возбуждений образца с целью обнаружения всех типов возбуждений, присутствующих в четной и нечетной частях спектра (путем Фурье-анализа компонент при измерении S_even(t,q), S_odd(t,q) и обратного Фурье-преобразования для определения искомой функции рассеяния S(ω,q) изучаемого образца).

Поставленная задача достигается тем, что в известном способе исследования структурно-динамических свойств вещества с помощью рассеяния нейтронов, заключающемся в том, что на исследуемый образец направляют пучок поляризованных нейтронов, вектор поляризации которых прецессирует в магнитных полях до и после образца, и измеряют косинус-Фурье-образ интегральной по энергетическому спектру нейтронов поляризации, по которой судят об атомной и молекулярной динамике вещества, связанной с четной частью его частотного спектра возбуждений, новым является то, что на выходе второго поля прецессии создают поле, вращающее поляризацию вокруг оси, перпендикулярной осям предшествующих вращений, и дополнительно измеряют синус-Фурье-образ интегральной по энергетическому спектру нейтронов поляризации, определяют нечетную составляющую частотного спектра возбуждений образца и получают полную информацию о структурно-динамических свойствах вещества, содержащуюся в четной и нечетной составляющих частотного спектра возбуждений в нем.

При анализе патентной и научно-технической литературы не было обнаружено заявляемой совокупности признаков, что свидетельствует о соответствии заявляемого объекта критерию "новизна".

Существенное отличие предлагаемого метода от известного уровня заключается в создании такой конфигурации магнитных полей по траектории нейтронного пучка, которая обеспечивает измерение Фурье-образа нечетной части спектра, а затем после измерения его четной части по способу-прототипу - восстановление всего спектра. Тем самым предлагаемый метод позволяет достигнуть качественно более глубокого уровня анализа структурно-динамических свойств вещества в реальном времени с высоким разрешением, что невозможно с помощью способа-прототипа и другими известными методами.

Известны отдельные исследования, когда наблюдались нечетные эффекты в частотном спектре возбуждений в кристаллах [4, 5, 6]. Однако до сих пор не было предложено метода, позволяющего анализировать временные спектры, связанные с нечетной динамикой.

Это, на наш взгляд, свидетельствует о соответствующем изобретательском уровне заявляемого способа.

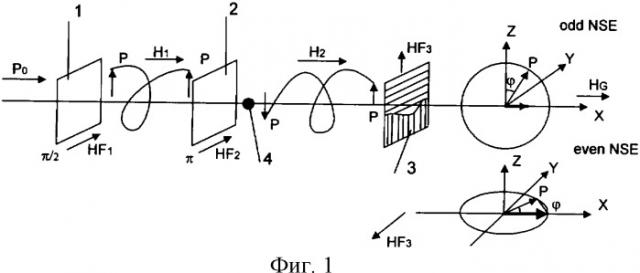
На фиг.1 условно показан принцип измерения нечетной (odd) и четной (even) компонент (S_odd(t,q) и S_even(t,q)) Фурье-образа функции рассеяния образца S(ω,q). Показаны вращатели поляризации нейтронов (флипперы 1-3) и образец 4.

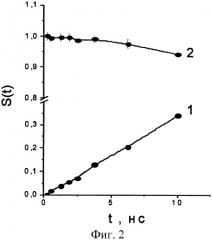
На фиг.2 приведены результаты измерения Фурье-образов нечетной (1) и четной (2) компонент функции рассеяния для образца феррожидкости (ФЖ) - коллоидного раствора, содержащего 20 об.% феррочастиц Fe₃O₄ диаметром 10 нм. Феррочастицы покрыты поверхностно-активным веществом (ПАВ, бислой олеиновой и додецилбензолсульфоновая кислоты). Это предотвращает агрегацию и стабилизирует ансамбль частиц, находящихся в тепловом движении.

Данные (1, 2) неупругого рассеяния нейтронов (длина волны λ=0.6 нм, угол рассеяния θ=1.7°, переданный импульс q=0.3 нм^-1) на образце ФЖ представляют собой нечетную и четную корреляционные функции S(t) в зависимости от времени в диапазоне t=0-10 нс.

Четная компонента (2) в гауссовом приближении S(t)=S_even(t)=exp[-q²Г(t)/2] зависит от среднего смещения частицы ΔХ=Г(t)^1/2=[a²+(vt)²]^1/2, где а=0.4±0.1 нм - амплитуда быстрых колебаний, v=8.7±0.3 см/с - компонента скорости частицы вдоль импульса q. Совершая колебания малой амплитуды, частица медленно дрейфует. Скорость ее дрейфа v=8.7 см/с на порядок меньше оценки тепловой скорости частицы V_T=(kT/m_P)^1/2˜100 см/с (m_P - масса частицы). Следовательно, частица увлекает при движении растворитель и соседей, затрагивая две координационные сферы объемом в 100 раз больше объема самой частицы.

В отличие от слабо меняющейся четной компоненты (ΔS_even˜5%), нечетная корреляционная функция (1), растущая в несколько раз быстрее в том же диапазоне времени, отражает не тепловое движение отдельных частиц, а коллективную динамику ансамбля. В ансамбле феррочастиц нейтроны возбуждают мягкие моды частотой ˜3·10⁷ рад./с и периодом Т=2π/<ω>˜200 нс. Отношение <ω>/q˜U˜10 см/с дает оценку скорости распространения такой мягкой моды, которая на 4 порядка ниже, чем у акустических волн в жидкости. Наблюдение "нечетной" динамики позволяет судить о тонких эффектах взаимодействия частиц в ФЖ, приводящих к возбуждению коллективных мод в ансамбле феррочастиц, тогда как "четная" динамика показывает лишь тепловое движение частиц.

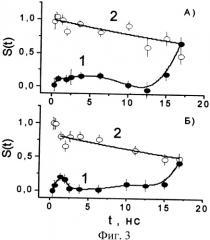
На фиг.3 представлены результаты измерения Фурье-образов нечетной и четной (1, 2) компонент частотной функции рассеяния для раствора поли-N-винилкапролактама в тяжелой воде (ПВКЛ, молекулярная масса М=1·10⁶, содержание полимера в растворе С=1.4 мас.%) в тяжелой воде при импульсе q=0.55 нм^-1˜1/L_S порядка обратного масштаба сегмента цепи (L_S˜2 нм) и температурах T₁=25.9°С и Т₂=26.2°С (А, Б), близких к точке конформационного перехода клубок-глобула (Т_C=32°С) [7]. Обнаружена сильная зависимость нечетной части от температуры. При T₁ наблюдается широкий максимум S_odd(t) в интервале t=0-12 нс и быстрый рост S_odd(t) при t>12 нс, тогда как при Т₂>T₁ максимум сравнительно узкий и занимает область t=0-4 нс, а при больших временах наблюдается слабое изменение S_odd(t) при t<15 нс. Нечетная часть демонстрирует быструю сегментальную релаксацию в согласии с модельной функцией S_odd(t/τ)=S_oo·(t/τ)·exp(-t/τ) с параметрами: S_oo1=0.47±0.09; τ₁=3.1±0.5 нс; S_oo2=0.41±0.17; τ₂=1.1±0.3 нс при температурах T₁ и Т₂. Время релаксации для данной релаксационной моды, возбуждаемой нейтроном при рассеянии на полимерной цепи, уменьшается в три раза при нагревании системы всего на 0.3°С, что указывает на коллективный характер данного возбуждения, пространственный масштаб которого должен быть сопоставим с размером клубка ПВКЛ. С другой стороны, четная часть следует обычной для сегментальной диффузии автокорреляционной функции S_even(t)=S_o·exp(-Dq²е) с параметрами: S_o1=0.995±0.049, D₁=(2.5±0.8)·10^-6 см²/c при Т=T₁; S_o2=0.836±0.041, D₂=(3.1±0.7)·10^-6 см²/с при Т=Т₁. При указанных температурах константы диффузии близкие и дают гидродинамический диаметр частицы D_H=kT/3πη≈1.6 нм на уровне размера сегмента. Таким образом, данные, предоставляемые измерениями по способу-прототипу, ограничены всего лишь локальными событиями и не позволяют судить о коллективной динамике объекта, которая отражена в нечетной части спектра.

Природа обнаруженной нечетной динамики становится ясной из модели резонанса шириной δ на частоте ω_о. Резонанс имеет частотный спектр S(ω,ω_o)=[(ω-ω_o)²+δ²]^-1. Для случая мягкой моды (ω_о˜δ) в первом приближении имеем сумму четной и нечетной частей S(ω,ω_o)≈(ω²+δ²)^-1-2ω_оω(ω²+δ²)^-2 и функции S_even(tδ)=exp(-tδ); -S_odd(t/τ)=A_ω·(tδ)·exp(-tδ), где А_ω=ω_о/δ при условии нормировки S_even(t=0)=S_0even=1, параметр δ=1/τ связан с временем релаксации. При Т₂ амплитудные параметры, S_0even=1-S_o2=0.16, S_oo2=0.41, дают величину А_ω=ω_о/δ=S_oo2/S_0even=2.6 и частоту ω_о=δ(S_oo2/S_0even)=2.3·10 рад./с. Период молекулярных колебаний на данной частоте 2π/ω_o˜3·10^-9 c на 3 порядка выше, чем период крутильных колебаний отдельных звеньев (˜10^-12 с). Следовательно, данная мода характеризует именно коллективную динамику клубка (˜10⁴ звеньев).

В соответствии с фиг.1 заявляемый способ заключается в следующем. Пучок монохроматизированных нейтронов с поляризацией Р_о, направленной вдоль скорости по оси X, проходит через флиппер 1, поле которого HF1 имеет направление, поперечное поляризации, и поворачивает вектор поляризации Р_о на угол π/2 в плоскость (Y, Z), ортогональную скорости нейтрона. Далее происходит прецессия вектора поляризации Р вокруг магнитного поля H₁ в первой области прецессии перед образцом. Прецессирующий вектор поляризации нейтронов лежит в плоскости (Y, Z). На границе первой области прецессии вектор поляризации поворачивается флиппером 2 на угол π. Затем нейтроны, рассеянные в образце 4 на определенный угол θ, которому отвечает значение упругого переданного импульса q=(4π/λ)sin(θ/2), двигаются через вторую область прецессии с полем Н₂ того же направления, что и в первой области. Магнитные поля первого и второго флипперов, HF1 и НF2, направлены вдоль оси Y. На выходе второй области прецессии нейтроны попадают в поле флиппера 3 HF3, ориентация которого задается двумя способами. Чтобы измерить Фурье-образ нечетной компоненты функции рассеяния, поле HF3 флиппера 3 выставляют вдоль направления Z поперечного направлению полей флипперов 1, 2 (т.е. на выходе второго поля прецессии создают поле, вращающее поляризацию вокруг оси, перпендикулярной осям предшествующих вращений). После вращения вокруг поля HF3 флиппера 3 вектор поляризации нейтронов Р имеет проекцию на направление ведущего поля HG (по оси X), равную P_X=Р·sinϕ. Здесь ϕ=ωt - результирующая фаза прецессии вектора поляризации после прохождения пучка через оба поля прецессии, t - время, - частота, связанная с энергией ΔЕ, переданной нейтрону при рассеянии. В эксперименте измеряется интегральная по частотному спектру неупругого рассеяния компонента поляризации <Р_X>˜S_odd(t,q). Напряженность полей прецессии H₁=H₂ варьируется, чтобы получить зависимость указанных Фурье-образов от времени где N(H) - число оборотов вектора поляризации в области поля прецессии Н для нейтрона с энергией Е. Эта компонента и дает искомый Фурье-образ нечетной части спектра S_odd(t,q). Чтобы измерить Фурье-образ четной компоненты функции рассеяния образца, поле в флиппере 3 ориентируют по оси Y. Затем производят измерение компоненты поляризации Р_X=P·cosϕ, что дает <Р_X>˜˜S_even(t,q). Так в результате измерений при двух ориентациях поля флиппера 3 определяют нечетный и четный Фурье-образы функции рассеяния, тем самым получают полную информацию о динамике образца. Общепринятый метод измерения поляризации нейтронов описан в работе [8].

Дополнительно здесь необходимо отметить, что показанная на фиг.1 эволюция вектора поляризации нейтронов в полях прецессии Н_{1, 2} и полях HF1, HF2, HF3 флипперов 1-3 относится к ситуации, когда поляризация нейтронов не меняется при рассеянии в образце, а возможно только изменение их энергии. В областях прецессии, сформированных флипперами 1-3, поляризация набирает фазу ϕ=γ_L(L₁H₁/v₁-L₂H₂/v₂), где L₁, L₂ - протяженности полей, γ_L - гиромагнитное отношение, v₁ и v₂ - скорости нейтрона в полях. В итоге поляризация, нормированная на исходную величину Р_о, приобретает компоненты Р_Y/Р_о=sinϕ, P_Z/P_o=cosϕ на выходе второго поля прецесии, т.е. перед флиппером 3.

Дальнейший анализ Z-компоненты в методе-прототипе, где флипперы 1-3 находятся в параллельной позиции (поля HF1, HF2, HF3 направлены по оси Y), приводит к определению Фурье-образа четной части частотного спектра S_even(t,q)˜. Обратное Фурье-преобразование позволяет восстановить четную часть спектра S_even(ω,q)=[S(ω,q)+S(-ω,q)]/2. Однако данные, полученные с помощью метода-прототипа, не содержат информации о нечетной части спектра S_odd=[S(ω,q)-S(-ω,q)]/2.

Следовательно, полный спектр S(ω,q)=S_even(ω,q)+S_odd(ω,q) из них не может быть восстановлен. Таким образом, корректное применение метода-прототипа возможно лишь для систем, имеющих четный спектр. Это не только вносит существенные ограничения к применению способа-прототипа, но и вообще в конкретном опыте не позволяет сделать заключение о корректности результатов, так как полный спектр S(ω,q) остается неизвестным.

Суть заявляемого способа заключается в определении Фурье-образа нечетной части путем создания специальной конфигурации магнитных полей флипперов, при которой флиппер 3 создает поле, перпендикулярное полям флипперов 1, 2 (т.е. на выходе второго поля прецессии создают поле, вращающее поляризацию вокруг оси, перпендикулярной осям предшествующих вращений). Это позволяет провести анализ компоненты поляризации на выходе второго поля прецессии Р_Y/Р_о=sinϕ и в итоге получить Фурье-образ нечетной части частотного спектра образца. Существенное отличие заявляемого способа от известных методов нейтронной спектроскопии среднего разрешения (время-пролетный, кристалл-дифракционный) [9], измеряющих частотную функцию рассеяния S(ω,q), заключается в том, что с помощью заявляемого метода отдельно определяется Фурье-образ нечетной части S(ω,q), содержащий данные о новых, неизвестных ранее, свойствах вещества. Имеются в виду данные неупругого рассеяния нейтронов, когда в среднем по спектру рассеянных нейтронов наблюдается увеличение или уменьшение их энергии. При этом с высоким разрешением (˜10^-9 эВ) детектируются спектр возбуждений (например, мягкие осциллирующие или релаксационные коллективные моды в ансамблях наночастиц и макромолекулах, фиг.2, 3). В измерениях с помощью указанных известных методов [2], [3] нечетная часть оказывается скрытой, она маскируется четной частью спектра, что не позволяет получить информацию о тонких эффектах нечетной динамики, подобных тем, что впервые обнаружены автором для феррожидкости и полимера (фиг.2, 3).

Результаты, полученные для феррожидкости и полимера, впервые дают представление о четной и нечетной динамике наносистем, о своеобразии неизвестных ранее явлений, связанных с нарушением четности функции рассеяния. Новая область NSE открывает возможности исследования неравновесных состояний, стохастической динамики, нелинейных возбуждений наноскопических систем, многие другие явления, бывшие за пределами экспериментальных возможностей.

Конкретно на приведенных примерах (фиг.2, 3) показано, что измерение нечетной части спектра возбуждений в молекулярных системах позволяет обнаружить неизвестные ранее явления коллективной динамики в виде мягких колебательных (релаксационных) мод. Анализ параметров этих мод позволяет судить о природе и потенциалах взаимодействия частиц, взаимосвязи структуры и динамики конденсированных сред, получая новое знание о микроскопических свойствах вещества, что невозможно другими известными методами. Тем самым предлагаемый метод позволяет достигнуть качественно более высокого уровня анализа атомной и молекулярной динамики вещества, что невозможно с помощью способа-прототипа и другими известными методами.

Исследование нечетных эффектов в динамике конденсированных сред имеет фундаментальное значение. Нарушение четности следует из принципа детального равновесия [10]. В физических системах при заселенности уровней энергии по Больцману переходы с низких уровней на более высокие являются более вероятными, чем обратные переходы, что приводит к следующему соотношению для функции рассеяния: В равновесных системах равенство S(-ω,-q)≈S(ω,q) достигается при малых переданных энергиях (низкочастотные возбуждения).

В примерах (фиг.2, 3) фактор весьма мал и не может быть причиной обнаруженных эффектов нарушения четности в динамике. Эти эффекты показывают, что изученные системы на уровне наноскопических масштабов не достигают равновесной заселенности энергетических уровней. В отличие от известных методов изучения четной динамики, предлагаемый метод позволяет анализировать тонкие эффекты поведения наносистем во времени, обусловленные отклонениями от равновесных состояний. Получение новых знаний в этой области недоступно другим известным методам, что доказывает преимущества предлагаемого способа изучения динамики вещества с высоким энергетическим разрешением в особенности для широкого класса необратимых явлений и стохастических процессов [11]. Среди немногих примеров анализа нечетных эффектов в динамике, когда среднее разрешение по энергии достаточно и работают известные методы неупругого рассеяния нейтронов (кристалл-дифракционный метод), следует упомянуть эксперименты по обнаружению трехспиновых корреляций при фазовых переходах второго рода [4, 5] и киральное рассеяние в магнетиках [6]. В качестве перспективного круга задач здесь можно назвать анализ динамики полимеров вблизи θ-температуры, когда изчезают парные взаимодействия звеньев, удаленных по цепи, и становятся существенными молекулярные корреляции высоких порядков [12].

Конкретная реализация способа (фиг.2,3) выполнена на нейтронном пучке (длина волны λ=0.6 нм, Δλ/λ=0.1) для образцов феррожидкости и раствора полимера известных химических составов и рассеивающей способности в Петербургском институте ядерной физики РАН.

Результаты испытаний, приведенные на фиг.2, 3, свидетельствуют о технической реализации способа, доказывают работоспособность способа и его эффективность для решения задач по исследованию структурно-динамических свойств наносистем (полимеров, коллоидов, систем с наночастицами - фуллеренами, нанокристаллами).

На основании данных испытаний для магнитных коллоидов и полимерных растворов следует заключить, что способ найдет применение в исследованиях динамики наноскопических систем и новых функциональных материалов, технологиях их производства для контроля функциональных свойств и оптимизации технологических процессов, мониторинге свойств материалов при длительной эксплуатации, экстремальных воздействиях (механические нагрузки, температуры, давления, проникающие излучения и др.).

Преимущества способа по отношению к прототипу и другим известным подходам (приведенные аналоги, методы анализа динамики по времени пролета нейтронов, кристалл-дифракционные методы) заключаются в следующем:

1. достигается разделение и дифференциальный анализ нечетной и четной компонент неупругого сечения рассеяния наноскопических объектов, что позволяет судить в целом о характере динамики, наличии процессов релаксации и мягких колебательных мод и дает новое знание о динамике вещества на атомном и молекулярном уровне;

2. гарантирует определение динамических характеристик объектов (констант диффузии, времен релаксации затухающих мод и частотного спектра возбуждений) в широком временном диапазоне 10^-12-10^-7, недоступном перечисленным выше методам;

3. способ является неразрушающим и не возмущает структуру и состояние образцов (так же, как и прототип).

Литература

1. А.С. №1673934, RU.

2. Лебедев В.Т., Д.Торок. Анализ квазиупругого рассеяния нейтронов в конденсированных средах периодическими пространственными фильтрами.//Письма в ЖТФ. 1999. Т.25. N 3. С.77-81.

3. F.Mezei. Neutron Spin-Echo: a new concept in polarized neutron techniques.//Z.Physik. 1972. V.255. P.146-160 - прототип.

4. Гукасов А.Г., Окороков А.И., Ф.Фужара, О.Шерп. О возможности исследования динамики трехспиновых корреляций в ферромагнетиках выше Т_с методом псевдослучайной модуляции поляризации нейтронов. Письма в ЖЭТФ. 1983. т.37.

5. Малеев С.В. Рассеяние поляризованных нейтронов в магнетиках. УФН. 2002., т.172, №6, с.617-646.

6. Plakhty V.P., Kulda J., Visser D., Moskvin E.V., Wosnitza J. Chiral critical exponents of the triangular-lattice antiferromagnet CsMnBr3 as determined by polarized neutron scattering. Phys. Rev. Lett. 2000. V.85, N18. P.3942-3945.

7. Lebedev V., Torok Gy., Cser L., Treimer W., Orlova D., Sibilev A. Polymer hydration and microphase decomposition in poly (N-vinylcaprolactam)-water complex. Appl. Cryst. 2003. V.36, P.967-969.

8. Абов Ю.Г., Гулько А.Д., Крупчицкий П.А. Поляризованные медленные нейтроны. М., Атомиздат, 1966, с.268.

9. Турчин В.Ф. Медленные нейтроны. М., Госатомиздат, 1963, с.372.

10. Bee М. Quasielastic Neutron Scattering. Bristol and Phyladelphia: A.Hilger, 1988, p.373.

11. Гинзбург С.Л., Савицкая Н.Е. Самоорганизация критического состояния в гранулированных сверхпроводниках. Материалы XXXIII зимней школы ПИЯФ РАН.

12 Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука. 1989, с.342.

Способ исследования структурно-динамических свойств вещества с помощью неупругого рассеяния нейтронов, заключающийся в том, что на исследуемый образец вещества направляют пучок поляризованных нейтронов, вектор поляризации которых прецессирует в магнитных полях до и после образца, и измеряют косинус-Фурье-образ интегральной по энергетическому спектру нейтронов поляризации, по которой судят о структурно-динамических свойствах вещества, связанных с четной частью его частотного спектра возбуждений, отличающийся тем, что на выходе второго поля прецессии создают поле, вращающее поляризацию вокруг оси, перпендикулярной осям предшествующих вращений, и дополнительно измеряют синус-Фурье-образ интегральной по энергетическому спектру нейтронов поляризации, определяют нечетную составляющую частотного спектра возбуждений образца и получают полную информацию о структурно-динамических свойствах вещества, содержащуюся в четной и нечетной составляющих частотного спектра возбуждений в нем.