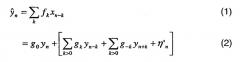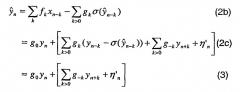Способ и устройство для гибридной коррекции с решающей обратной связью

Способ и устройство для гибридной коррекции с решающей обратной связью

Иллюстрации

Показать все

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится, в общем, к коррекции принятого сигнала и более конкретно к гибридной коррекции с решающей обратной связью.

Уровень техники

При передаче цифровой информации обычно используется модулятор, который отображает цифровую информацию в аналоговых сигналах. Это отображение обычно выполняется на блоках битов, содержащихся в информационной последовательности, подлежащей передаче. Сигналы могут отличаться друг от друга амплитудой, фазой, частотой или их комбинацией. Затем данная информация передается как соответствующий сигнал. Процесс отображения из цифровой области в аналоговую область называется модуляцией.

В беспроводной системе связи модулированный сигнал передается по радиоканалу. Затем приемник демодулирует принятый сигнал, чтобы извлечь из него исходную цифровую информационную последовательность. В приемнике переданный сигнал подвергается воздействию линейных искажений, вводимых каналом, а также внешнего аддитивного шума и помех. Характеристики канала обычно изменяются во времени, и поэтому они не известны априори для приемника. Приемники компенсируют искажения и помехи, внесенные каналом, различными способами. Один способ компенсации искажений и уменьшения помех в принятом сигнале заключается в применении эквалайзера (корректора). Коррекция обычно включает в себя методы, используемые для уменьшения эффектов искажения в канале связи. Из принятого сигнала эквалайзер вырабатывает оценки исходной цифровой информации.

Известные способы коррекции построены на основе предположений, касающихся принятого сигнала. Такие предположения обычно не корректны для различных сценариев кодирования, модуляции и передачи, и поэтому работа этих эквалайзеров во многих условиях бывает неудовлетворительной. Кроме того, известные эквалайзеры с использованием решающей обратной связи часто страдают от эффектов распространения ошибок, которые усиливают действие изолированных ошибок решения. Также в процессе решающей обратной связи используются жесткие решения для каждого символа и не учитывается вероятность того, что решение символа правильное.

Таким образом, существует потребность в способе коррекции, который бы уменьшал линейные искажения в принятом сигнале в широком спектре рабочих условий. Также существует потребность в уменьшении распространения ошибок в эквалайзере с решающей обратной связью. И еще существует потребность в обеспечении степени правдоподобия для процесса с решающей обратной связью.

Краткое описание чертежей

Фиг.1А изображает структурную схему компонентов системы связи,

фиг.1В детально изображает часть системы связи по фиг.1А,

фиг.2 изображает концептуальную модель эквалайзера с решающей обратной связью в системе связи,

фиг.3 изображает структурную схему эквалайзера с решающей обратной связью, подобного изображенному на фиг.2,

фиг.4 изображает математическую модель ограничителя уровня символа,

фиг.5 изображает алгоритм оптимизации коэффициентов фильтров в эквалайзере с решающей обратной связью,

фиг.6 изображает алгоритм адаптивной фильтрации по методу наименьших средних квадратов для оптимизации коэффициентов фильтров в эквалайзере с решающей обратной связью,

фиг.7 изображает алгоритм адаптивной фильтрации по методу наименьших средних квадратов для оптимизации коэффициентов фильтров в эквалайзере с решающей обратной связью для системы с использованием периодического пакетного пилот-сигнала,

фиг.8А изображает отображение совокупности для 8-позиционной фазовой манипуляции (PSK),

фиг.8В иллюстрирует области сетки, использованные для решений мягкого ограничителя, наложенные на отображение совокупности на фиг.8А,

фиг.9А изображает отображение совокупности для случая бинарной фазовой манипуляции (BPSK), или 2-PSK,

фиг.9В иллюстрирует области сетки, использованные для решений мягкого ограничителя, наложенные на отображение совокупности на фиг.9А,

фиг.10 изображает эквалайзер с решающей обратной связью, в котором реализуется процесс решения "с мягким ограничением",

фиг.11 изображает процесс решения "с мягким ограничением",

фиг.12 изображает процесс решения "с мягким ограничением", в котором применяется вычисление ряда Тейлора,

фиг.13 изображает структурную схему "мягкого ограничителя",

фиг.14 изображает структурную схему "мягкого ограничителя" с применением вычисления ряда Тейлора.

Подробное описание изобретения

В данном контексте слово "примерный" используется в смысле "служащий в качестве примера, случая или иллюстрации". Любой вариант, описанный как "примерный", не следует обязательно считать предпочтительным или имеющим преимущество по сравнению с другими вариантами.

На фиг.1А показана часть компонентов системы связи 100. В дополнение к проиллюстрированным блокам в систему связи можно ввести другие блоки и модули. Биты, вырабатываемые источником (не показан), кадрируются, кодируются и затем преобразуются в символы в сигнальной совокупности. Последовательность двоичных чисел, сформированная источником, называется информационной последовательностью. Информационная последовательность кодируется кодером 102, который выдает битовую последовательность. Выходной сигнал кодера 102 подается в блок 104 отображения, который служит в качестве интерфейса с каналом связи. Блок 104 отображения отображает выходную последовательность кодера в символах y(n) в комплексной оцененной сигнальной совокупности. Дальнейшая обработка передачи, включая блоки модуляции, а также канал связи и обработка аналогового приемника смоделированы секцией 120.

На фиг.1В показаны некоторые детали, входящие в состав секции 120 на фиг.1А. Как видно на фиг.1В, комплексные символы y(n) модулированы на импульсе аналогового сигнала, а полученный комплексный модулирующий сигнал синусоидально модулирован на синфазной и квадратурной ветвях несущего сигнала. Полученный аналоговый сигнал передается ВЧ антенной (не показана) по каналу связи. Таким образом можно использовать целый ряд схем модуляции, например, M-арную фазовую манипуляцию (М-PSK), 2^M-арную квадратурную амплитудную модуляцию (2^M QAM) и т.п.

Каждая схема модуляции имеет соответствующую "сигнальную совокупность", которая отображает один или несколько битов в уникальном комплексном символе. Например, при модуляции типа 4-PSK два закодированных бита отображаются одним из четырех возможных комплексных значений {1,i,-1,-i}. Следовательно, каждый комплексный символ y(n) может принимать четыре возможных значения. В общем, для M-PSK log₂M кодированных битов отображаются одним из М возможных комплексных значений, лежащих на единичном круге комплекса.

Также на фиг.1В показано, что в приемнике аналоговый сигнал подвергается понижающему преобразованию, фильтрации и выборке, например, с подходящим кратным частоты Найквиста. Полученные выборки обрабатываются эквалайзером 110, который корректирует искажения сигнала и другой шум и помехи, внесенные каналом, как смоделировано секцией 120. Эквалайзер 110 выдает оценки переданных символов y(n). Эти оценки символов затем обрабатываются декодером для определения исходных информационных битов, т.е. битов источника, которые были введены в кодер 102.

Комбинация импульсного фильтра, I-Q модулятора, канала и аналогового процессора на входном каскаде приемника, показанная на фиг.1А и 1В, моделируется линейным фильтром 106, имеющим импульсную характеристику {h_k} и z-преобразование H(z), в котором введенные каналом помехи и шум моделируются как аддитивный белый гауссов шум (АБГШ).

На фиг.1В детально изображена секция 120, содержащая блок обработки 122 входного каскада, подсоединенный к фильтрам 126 и 128 основной полосы для обработки синфазной (I) и квадратурной (Q) компонент, соответственно. Каждый фильтр 126, 128 основной полосы далее подключен к умножителю для умножения на соответствующую несущую. Полученные сигналы затем суммируются в суммирующем блоке 134 и передаются по каналу связи в приемник. В приемнике блок 142 аналоговой предварительной обработки принимает переданный сигнал, который обрабатывается и подается в согласованный фильтр 144. Выходной сигнал согласованного фильтра 144 затем подается в аналогоцифровой преобразователь (A/Ц) 146. Следует отметить, что можно использовать и другие модули в соответствии с конструктивными и операционными критериями. Компоненты и элементы на фиг.1А и 1В представлены в целях обеспечения понимания следующего описания и не предназначены для полного описания системы связи.

Как было описано выше, последовательности передаваемых символов обозначены как {y(n)}. Для целей данного описания предположим, что символы {y(n)} нормированы по средней единице энергии, т.е. E|y_n|²=1. Если выходной сигнал канала подвергнуть фильтрации и выборке с частотой символов (которая может быть, хотя и не обязательно, равна частоте Найквиста), то выходной сигнал канала будет:

где η_n - белый гауссов шум с дисперсией (E_s/N₀)^-1. Эквалайзер обычно реализуется как линейный фильтр с коэффициентами {f_k} и характеризуется z-преобразованием F(z). Пусть означает выходной сигнал эквалайзера, где определяется как:

где G(z)=F(z)H(z) и

Следует отметить, что второй член в квадратных скобках [...] в ур.(2) представляет межсимвольные помехи (ISI) и шум. Первый член ур.(2) соответствует помехам, связанным с прошлыми символами, а второй член соответствует помехам, связанным с будущими символами. Первый член часто называют "причинными" ISI, а второй член часто называют "антипричинными" ISI. Если разработчик предполагает, что прошлые символы были обнаружены корректно, то член причинных ISI можно удалить. В идеальном случае, если эквалайзеру известны символы совокупности y_n-1, y_n-2,K, т.е. символы совокупности, переданные до момента времени n, при определении оценки эквалайзер может удалить часть межсимвольных помех путем вычитания первого члена [...] ур.(2). Однако в практических системах эквалайзеру известны только ранее сформированные оценки символов, такие как , ,K. Если помехи и шум достаточно малы, то можно ожидать, что эти решения символов на оценке дадут исходный переданный символ y_n совокупности. Устройство, выполняющее такие решения для символов, называется "ограничитель" и его работа обозначена как σ(.). При этом приемник может сформировать оценку причинных ISI с помощью последовательности решений для символов из ограничителя и вычесть эту оценку из выходного сигнала эквалайзера, чтобы получить:

в предположении, что σ()≈y_n-k. В этом состоит основной принцип коррекции с обратной решающей связью, при которой причинные ISI удаляются посредством причинной фильтрации решений для символов, выполненных ограничителем уровня символов, оперирующим на выходе эквалайзера.

На фиг.3 показана система связи 350, в которой используется эквалайзер 340 с решающей обратной связью (ЭРОС). Система связи 350 смоделирована таким образом, что она имеет эквивалентный линейный канал 352, который фильтрует последовательность символов y_n. Шум и помехи, η_n, добавляются в суммирующем блоке 354, и выходной сигнал x_n означает выборки сигнала, полученные после обработки входным каскадом и выборки в приемнике. ЭРОС 340 обрабатывает x_n и фильтрует x_n, чтобы сформировать оценку . ЭРОС 340 смоделирован с линейным фильтром 356 прямой связи и линейным фильтром 358 обратной связи. Фильтр 356 прямой связи имеет коэффициенты отводов, обозначенные как {f_k}, и применяет z-преобразование F(z). ЭРОС 340 также содержит чисто причинный фильтр 358 обратной связи, подключенный к ограничителю 360, образующий петлю обратной связи, которая формирует оценку причинных ISI. Иными словами, фильтр 358 обратной связи удаляет из оценки настоящего символа часть ISI, вызванную ранее обнаруженными символами. Оценка причинных ISI из фильтра 358 обратной связи подается в суммирующий блок 308, который вычитает оценку причинных ISI из выходного сигнала фильтра 356 прямой связи. Полученный выходной сигнал суммирующего блока 308 является выходным сигналом эквалайзера. Выходной сигнал эквалайзера также является оценкой переданного символа y_n и подается в декодер 364 для определения исходной информационной последовательности.

Ограничитель 360 обрабатывает выходной сигнал эквалайзера из суммирующего блока 308 и в ответ принимает решение относительно исходного символа у_n. Выходной сигнал ограничителя 360 затем подается в чисто причинный фильтр 358 обратной связи. Фильтр 356 прямой связи также называется "ФПС". Фильтр 358 обратной связи также называется "ФОС". В ЭРОС оптимизация коэффициентов фильтров фильтра 356 прямой связи и фильтра 358 обратной связи прямо влияет на работу эквалайзера. Устройство, которое выполняет данную оптимизацию, на фиг.3 обозначено как оптимизатор 362 коэффициентов. Существует целый ряд путей оптимизации коэффициентов фильтров. Традиционно коэффициенты ФПС и ФОС оптимизируются в неявном предположении, что решения ограничителя для символов совершенно надежны и что причинные ISI, т.е. помехи от прошлых символов, совершенно удаляются с помощью ФОС. При этом предположении коэффициенты ФПС оптимизируются таким образом, чтобы член остаточных помех и шума в ур.(3) был малым. Более точно, z-преобразование ФПС, F(z), оптимизируется так, что в ур.(3) приближается к y_n в среднеквадратическом смысле.

На практике ФПС и ФОС часто реализуются фильтрами с конечной импульсной характеристикой (ФКИХ) и во время начального периода тренировки/преамбулы/адаптации ФПС и ФОС "тренируются" на символах пилот-сигнала в предположении совершенной работы ограничителя, т.е. σ()=y_n. Это реализуется посредством обхода ограничителя и обратной подачи локально сформированных (и поэтому правильных) символов пилот-сигнала, вместо ограниченных (а значит возможно ошибочных) решений для символов пилот-сигнала, в ФОС. Можно применить целый ряд алгоритмов для оптимизации коэффициентов фильтров во время периода тренировки, включая адаптивные алгоритмы, такие как алгоритм наименьших средних квадратов (НСК), рекурсивный алгоритм наименьших квадратов (РНК), алгоритм прямого обращения матриц и другие. После завершения тренировочного периода включается ограничитель 360, и ограниченные символы данных подаются обратно через ФОС.

Обычные алгоритмы оптимизации ЭРОС вносят ряд потенциальных проблем. В системах с применением сильного кодирования решения ограничителя часто имеют высокую частоту появления ошибочных символов (ЧОС). Например, в системе с применением совокупности среднего размера, такой как 16-QAM, и низкоскоростного турбокода, например, со скоростью 1/3, при работе на уровне частоты появления ошибочных пакетов величиной 1% часто встречается ЧОС 25% или выше. С другой стороны, коэффициенты ФПС и ФОС в ЭРОС обычно оптимизируются с неверным предположением, что решения ограничителя совершенно надежны.

Кроме того, коэффициенты ФПС и ФОС оптимизируются в предположении, что причинные ISI совершенно удалены. В результате антипричинные ISI уменьшаются за счет более высоких причинных ISI. Обычные алгоритмы оптимизации ЭРОС в смысле представленных уравнений (особенно ур.(1)-(3)) приводят к значениям g_k, которые имеют тенденцию быть больше для k>0, но меньше для k<0. Однако когда ЧОС ограничителя не является пренебрежимо малой, ошибочные решения для символов заражают ФОС и после этого вычитаются ошибочно. Когда значения g_k для k>0 большие, возрастают остаточные помехи, а это может приводить к дальнейшим ошибкам ограничителя на последующих символах. Такое явление называется распространением ошибок.

Попытки уменьшить распространение ошибок включают в себя обратную подачу ограниченных символов пилот-сигнала во время тренировки, в отличие от тренировки ФПС и ФОС посредством обратной подачи локально генерированных (а значит правильных) выборок пилот-сигнала. Ограниченные символы пилот-сигнала время от времени бывают ошибочными, что вынуждает соответственно корректироваться ФПС и ФОС. Однако этот способ также не лишен проблем. Ограниченные символы пилот-сигнала и ограниченные символы данных могут иметь очень разные частоты появления ошибок, так как символы пилот-сигнала обычно передаются через BPSK, т.е. 2-PSK (или другую меньшую совокупность), а символы данных обычно передаются через совокупность большего размера. В результате, ЧОС символов пилот-сигнала и символов данных могут быть совершенно разными. В этом случае коэффициенты ФПС и ФОС оптимизируются на основании ограниченных символов пилот-сигнала, и эффект этих коэффициентов в обработке символов данных приводит к работе ниже оптимального уровня.

Эти проблемы можно решить посредством оптимизации коэффициентов ФПС и ФОС в целях учета ошибок, обусловленных ограничителем 360 на фиг.3. Иными словами, оптимизатор 362 коэффициентов модифицируют, признавая, что из-за ошибок ограничителя причинные ISI невозможно удалить совершенно. Этот принцип отличается от известных методов, в которых неявно предполагается, что ограничитель свободен от ошибок, и поэтому причинные ISI совершенно удаляются.

Теория, положенная в основу одного варианта, заключается в моделировании работы ограничителя с помощью независимого, одинаково распределенного (н.о.р.) "канала", обозначенного Q(). Предполагается, что этот "канал" не зависит от шумового процесса, обозначенного как {η_n} в ур.(0), и передаваемой последовательности символов, обозначенной как {y_n}. Этот "канал" полностью характеризуется его условной плотностью Q(), где и y соответственно означают выходной сигнал ограничителя и действительный переданный символ. Допустим, что канал является причиной ошибочных символов в ФОС. На практике ошибочные символы возникают в пакетах, потому что ошибка ограничителя на текущем символе подразумевает, что следующие символы могут быть неправильно ограничены с более высокой вероятностью. В рассматриваемой упрощенной модели ограничителя предполагается, что ошибки ограничителя являются н.о.р.

На фиг.2 показана концептуальная модель 300 системы связи с эквалайзером с решающей обратной связью. Символы, переданные по каналу связи 302, смоделированному передаточной функцией H(z), искажены аддитивным шумом в суммирующем блоке 304. Результирующий сигнал фильтруется в ФПС 306. Оценка исходного переданного символа формируется путем вычитания вектора ошибок в суммирующем блоке 308. Оценка исходного переданного символа передается в декодер 316. Вектор ошибок формируется причинным фильтром 310 обратной связи, с передаточной функцией В(z), который фильтрует выходные сигналы "канала" 314. Вектор ошибок, сформированный фильтром 310 обратной связи, представляет оценку причинных ISI, присутствующих в выходном сигнале ФПС 306. "Канал" копирует статистическое поведение ограничителя 360 на фиг.3, т.е. статистическое соотношение между входным и выходным сигналами канала 314 идентично статистическому соотношению между переданным символом у_n и соответствующим выходным сигналом ограничителя 360. Оптимизатор 320 коэффициента осуществляет оптимизацию коэффициентов фильтров для ФПС 306 и ФОС 310. Следует отметить, что основное отличие между фиг.3 и фиг.2 заключается в замене ограничителя 360 концептуальной моделью "канала" Q() 314.

Как отмечалось выше, ограничитель смоделирован на фиг.2 посредством выбора "канала" Q(), чтобы смоделировать статистическое поведение действительного ограничителя без учета статистической зависимости ошибок ограничителя во времени. Так как действительный ограничитель оперирует с выходным сигналом эквалайзера, соответствующая маргинальная статистика содержит остаточные помехи. Пусть SINR представляет отношение сигнал/помеха+шум в выходном сигнале эквалайзера, т.е. в выходном сигнале суммирующего блока 308 на фиг.2. Допустим, что остаточные помехи и шум в выходном сигнале эквалайзера можно смоделировать как нулевую среднюю комплексную гауссову случайную переменную Z с независимыми действительной и мнимой частями, каждая с дисперсией σ², где

Маргинальная статистика определяется эквивалентным каналом Q(), в котором

где σ() означает функцию ограничения по минимальному расстоянию, определенную как

и Z в ур.(7) является нулевой средней комплексной гауссовой случайной переменной, моделирующей остаточные помехи со свойствами, описанными выше. На фиг.4 показан канал смоделированный согласно представленным выше предположениям и уравнениям. В частности, математическое описание 314 на фиг.2 показано в виде системы 380. Входной сигнал в ограничитель 384 обозначен как и смоделирован как переданный символ y, искаженный аддитивным шумом и помехами. Шум и помехи смоделированы комплексной гауссовой случайной переменной Z. Ограничитель 384 применяет функцию ограничения по минимальному расстоянию, как описано в ур.(8), чтобы получить выходной сигнал ограничителя, обозначенный Совместная статистика, объединяющая и y, составляет полное математическое описание модели канала Конструкция канала показанная на фиг.4, является новой и отличается от известных методов тем, что шум Z может иметь ненулевую дисперсию. В известных методах неявно предполагается, что Z тождественно равно нулю. Следовательно, в данной модели ограничителя предполагается наличие ошибок решения, в отличие от известных методов, в которых ограничитель предположительно лишен ошибок.

Пусть на фиг.2 f_Qи b_Q означают коэффициенты ФПС и ФОС, выбранные таким образом, чтобы минимизировать среднеквадратическую ошибку между переданным символом y_n (вход канала 302) и оценкой символа (выходом суммирующего блока 308). Иными словами, коэффициенты f_Q и b_Q являются оптимальной винеровской минимальной среднеквадратической ошибкой (MMSE). По причинам, которые будут описаны ниже, эти коэффициенты называются "винеровскими коэффициентами гибридного ЭРОС". Коэффициенты f_Q и b_Q можно определить посредством стандартной оптимизации Винера-Хопфа с применением следующего уравнения:

где R_F означает ковариацию содержаний ФПС, R_B - ковариацию содержаний ФОС, R_F,B - взаимную ковариацию содержаний ФПС и ФОС, и p_F - взаимную ковариацию между содержанием ФПС и переданным символом. Эти ковариации и взаимные ковариации зависят от линейного канала 302, описанного H(z). Допустим, что символы в Y, т.е. совокупности передачи используются с равной вероятностью, тогда ρ_Q определяется как

где |Y| означает количество элементов Y, т.е. количество возможных символов в совокупности передачи. Следовательно, для данного и канала с Z-преобразованием H(z) коэффициенты MMSE f_Q и b_Q определяются с помощью ур.(4) и (5).

Напомним, что Q() определялся согласно ур.(6) и (7) с применением гипотетического значения SINR на выходе эквалайзера. Применение ур.(4) и (5) приводит к получению коэффициентов MMSE f_Q и b_Q. Когда эти значения коэффициентов ФПС и ФОС используются в ФПС 306 и ФОС 310 на фиг.2, результирующее SINR на выходе эквалайзера может отличаться от исходного гипотетического значения SINR. Следовательно, гипотетическое значение SINR может быть состоятельным или несостоятельным. Однако состоятельное значение SINR, а значит и состоятельный набор коэффициентов MMSE f_Q и b_Q, можно найти путем итерации, т.е. использования вновь найденного значения SINR для определения нового "канала" нахождения нового набора соответствующих коэффициентов MMSE и т.д. Этот итеративный процесс можно схематически представить следующим образом:

В частности, итеративный алгоритм можно использовать для вычисления винеровского гибридного ЭРОС. Алгоритм данного варианта проиллюстрирован на фиг.5. Процесс 400 начинается с установки n=0 на этапе 402 и произвольного выбора SINR⁰. Этот процесс продолжается определением SINRⁿ и вычислением ρ(SINRⁿ) с помощью ур.(5),(6) и (7) на этапе 404. Коэффициенты f_n,b_n фильтров вычисляются на этапе 406 с помощью ур.(4). Согласно данному варианту изобретения, процесс вычисляет SINRⁿ⁺¹= SINR(f_n,b_n,SINRⁿ) на этапе 408. Следует отметить, что SINR(f,b,x) означает SINR на выходе эквалайзера с коэффициентами f ФПС и коэффициентами b ФОС и каналом Q(.|.) ограничителя с SINR х. Канал ограничителя определяется с помощью ур.(6) и ур.(7). Если процесс сходится в блоке решения 410, то обработка продолжается на этапе 412 установкой коэффициентов фильтров. Если процесс не сходится, обработка возвращается к этапу 404.

Следует отметить, что, как описано в итеративном алгоритме на фиг.5, значение SINR⁰ можно выбирать произвольно. Два предела, SINR⁰=0, SINR⁰=∞, соответствуют запуску с абсолютно ненадежным ограничителем или совершенным ограничителем, соответственно.

Следует отметить, что ρ представляет корреляцию между выходным сигналом ограничителя и действительно переданным символом, и ρ, как таковая, является функцией SINR выходного сигнала эквалайзера. Если выходной сигнал эквалайзера очень шумный, то эта корреляция низкая. В этом случае решения для символов ограничителя в основном ненадежные, и точная оценка причинных ISI невозможна. Как ожидается, в этом случае алгоритм на фиг.5 сходится к коэффициентам ФПС и ФОС, которые близко напоминают коэффициенты линейного эквалайзера, т.е. эквалайзера, в котором коэффициенты ФОС ограничены нулем. С другой стороны, когда выходной сигнал эквалайзера почти бесшумный, корреляция ограничителя ρ имеет тенденцию приближаться к единице. В этом случае алгоритм на фиг.5 сходится к коэффициентам ФПС и ФОС, которые близко напоминают коэффициенты "идеального" ЭРОС, т.е. ЭРОС с совершенно надежным ограничителем. Между этими пределами алгоритм на фиг.5 сходится к коэффициентам ФПС и ФОС, которые являются "гибридами" упомянутых двух ограничительных пределов. Такая "гибридизация" выполняется автоматически итеративным алгоритмом. По этой причине полученные таким образом коэффициенты ФПС и ФОС называются "гибридными коэффициентами ЭРОС".

Описанные выше варианты требуют явного знания канала H(z), чтобы построить различные ковариации и взаимные ковариации ур.(4). При этом винеровские гибридные коэффициенты ФПС и ФОС определяются путем решения ур.(4) для f_Q,b_Q. Однако на практике H(z) обычно не известно в приемнике, поэтому желателен альтернативный метод определения винеровских гибридных коэффициентов ЭРОС для ФПС и ФОС. Альтернативный вариант, именуемый как "адаптивный гибридный ЭРОС", не требует явного знания канала H(z). Сначала определим среднеквадратическую ошибку (MSE):

где X_n - содержание ФПС в момент времени n, Z_n - содержание ФОС в предположении безошибочной обратной связи, и Δ - ошибочные символы обратной связи, введенные "каналом" Так как предполагается, что ошибки, введенные являются н.о.р. и независимыми, ур.(9) можно записать следующим образом:

где E_Q означает "ожидание" в отношении Используя тот факт, что совокупность передачи нормирована по единице энергии, и определение ρ_Q в ур.(5), получаем:

где

Объединение ур.(9b) с ур.(9а) дает

Следует отметить, что появившийся в ур. (9с), можно интерпретировать как "энергию" в коэффициентах ФОС. Уравнение (9с) является отправной точкой для получения целого ряда адаптивных алгоритмов. Например, для получения адаптивного алгоритма на основе рекурсивного метода наименьших квадратов (РНК) новая функция стоимости определяется путем замены статистического ожидания на выборочное среднее, например, n=1,...,N. Затем применяются стандартные методы для получения рекурсивного оптимизатора этой функции стоимости. В одном варианте применяется оптимизатор РНК функции стоимости, определенный следующим образом:

где

Следует отметить, что α_Q можно назвать "модифицированной мерой энергии коэффициентов фильтра обратной связи" или "вектором коррекции ошибок". Оптимизацию РНК можно выполнять на символах пилот-сигнала, присутствующих в передаче.

Алгоритм наименьших средних квадратов: Другой вариант оптимизации ур. (9с) основан на алгоритме наименьших средних квадратов (НСК). Алгоритм НСК рекурсивно корректирует коэффициенты ФПС и ФОС гибридного ЭРОС, чтобы минимизировать MSE, определенную в ур. (9с). Для фиксированного канала корректировки алгоритма наименьших средних квадратов (НСК) определяются как

где MSE определено в ур.(9с), μ - размер шага НСК и E^- означает отброс статистического ожидания в определении ур.(9с). Вычисление частичных производных приводит к

Когда выбирается достаточно малое значение μ, последовательность итераций, определенная в ур.(11)-(13), стабильная и сходится к набору коэффициентов, которые решают ур.(4). Следует отметить, что эта последовательность итераций не требует явной оценки ковариаций и взаимных ковариаций в ур.(4).

На фиг.6 проиллюстрирован алгоритм НСК согласно одному варианту изобретения. Алгоритм 500 начинается с выбора исходного значения SINR⁰ на этапе 502. Кроме того, индекс k инициализируется как k=0. На этапе 504 оценивается значение SINR^k и вычисляется или определяется α(SINR^k) из заранее вычисленной справочной таблицы (СПТ). Ур.(11)-(13), приведенные выше, вычисляются итеративно на основании символов пилот-сигнала в передаче до тех пор, пока не будут удовлетворены критерии сходимости на этапе 506. Результат такой итерации определяет значения для (f_k,b_k). На этапе 508 процесс оценивает SINR^k+1, который является SINR на выходе эквалайзера, когда коэффициенты ФПС и ФОС равны (f_k,b_k). Эта оценка может быть выполнена с помощью символов пилот-сигнала при передаче. Затем процесс приращивает индекс k. После достижения сходимости SINR^k в блоке решения 510 процесс переходит к этапу 512 для применения коэффициентов фильтров. Затем процесс возвращается к этапу 504.

Алгоритм с периодическими пакетами пилот-сигнала. Согласно другому варианту изобретения, в системе связи применяются периодически передаваемые пакеты пилот-сигнала, которые используются приемниками для коррекции коэффициентов фильтров в эквалайзере приемника. Такая коррекция часто называется "тренировкой" эквалайзера. Примером такой системы является система, поддерживающая высокую скорость передачи данных (ВСД), которая описана в стандарте "TIA/EIA-IS-856 CDMA2000 High Rate Packet Data Air Interface Specification" (стандарте IS-856). В системе ВСД через каждые 0,833 мс передаются 96 символов пилот-сигнала. Каждая группа из 96 символов пилот-сигнала называется "пакетом пилот-сигнала". Между пакетами пилот-сигнала система ВСД передает символы данных, предназначенные для приемников. На фиг.7 показан алгоритм для применения гибридного ЭРОС на основе НСК в такой системе. Вначале алгоритм 600 устанавливает SINR⁰ равным 0 или ∞ на этапе 602. Первоначальный выбор SINR не указан и может быть неважным, хотя для обеспечения наиболее быстрой сходимости может быть предпочтительным SINR⁰ равный ∞. Также инициализируется индекс k, который устанавливается равным 0. На этапе 604 алгоритм определяет SINR^k и вычисляет α(SINR^k) или определяет необходимое значение путем обращения к заранее вычисленной справочной таблице. Исходные значения f и b устанавливаются как f₀=0 и b₀=0 на этапе 606. Во время (k+1)-го пакета пилот-сигнала процесс итерирует ур.(11)-(13) для всех элементов пакета пилот-сигнала на этапе 608. В данном примере ВСД алгоритм 600 осуществляет итерацию для 96 элементов пакета пилот-сигнала и сохраняет конечные значения f и b. На этапе 610 процесс оценивает SINR^k+1, используя 96 элементов предыдущего пакета пилот-сигнала. Во время части данных, следующей за (k+1)-ым пакетом пилот-сигнала, сохраненные значения f и b загружаются в ФПС и ФОС, и символы данных компенсируются стандартным методом с решающей обратной связью. На этапе 614 процесс вычисляет значение α(SINR^k+1) и приращивает k. Процесс продолжается применением этого алгоритма во время операций демодуляции.

Алгоритм на фиг.7 является адаптивным для медленно изменяющихся во времени каналов, как квази-устойчивое состояние SINR^k, и поэтому не ожидается, что α(SINR^k) сильно изменится в течение времени сходимости алгоритма НСК.

Мягкий ограничитель: Как обсуждалось выше, распространение ошибок существенно ограничивает использование ЭРОС в системах связи с кодированием каналов. Так как причинные ISI аннулируются путем обратной подачи решений для индивидуальных символов, одна изолированная ошибка решения может привести к пакету последующих ошибок решения, что существенно увеличит остаточные помехи на выходе эквалайзера. Если применяется сильное кодирование каналов, то вероятность ошибки решения для символа не является пренебрежимо малой (обычно она составляет около 25 процентов), и распространение ошибки может серьез