Способ вычисления сдвига в датчике перемещения с высокой разрешающей способностью

Способ вычисления сдвига в датчике перемещения с высокой разрешающей способностью

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к области навигационной техники и может быть использовано для создания датчиков перемещения и скорости.

В связи со стремительным развитием вычислительной техники и постоянным расширением областей ее применения, существует постоянно возрастающая потребность в устройствах ручного ввода координат (манипуляторы типа «мышь», трекболы и т.п.). Постоянно возрастают требования к их точности, разрешающей способности, быстродействию и другим параметрам.

В настоящее время широко известны устройства для ручного ввода координат, типа «оптическая мышь» (см. [1]), пришедшие на смену механическим манипуляторам благодаря более высокой надежности, разрешающей способности и другим преимуществам. Их работа основана на получении микрофотографий поверхности, по которой движется манипулятор (далее - рабочая поверхность), и вычислении относительного сдвига путем сравнения последовательно сделанных кадров. Они содержат в своем составе осветитель, 2-мерную фотоприемную оптическую матрицу, оптическую систему, формирующую изображение рабочей поверхности, на поверхности оптической матрицы и устройство обработки сигнала, получаемого с выхода оптической матрицы. Оптическая матрица формирует последовательность кадров, представляющих собой изображения рабочей поверхности, которые изменяются по мере того, как манипулятор перемещается вдоль рабочей поверхности.

Известен способ вычисления сдвига, описанный в [2], который включает следующие существенные шаги:

- Формирование изображения рабочей поверхности, по которой движется датчик, в виде 2-мерной непрерывной картинки, описываемой функцией А(х,y), на поверхности фотоприемной оптической матрицы

- Дискретизацию сформированного изображения в пространстве и во времени и представление его в виде последовательности кадров, в каждом из которых исходное изображение представлено дискретным набором точек A_j,j

- Запоминание кадра, сформированного в первый момент времени, в первом буфере памяти в качестве опорного кадра Aref_i,j

- Запоминание кадров, сформированных в последующие моменты времени, во втором буфере памяти в качестве текущего кадра Acur_i,j

- Вычисление сдвига между опорным и текущим кадрами путем их сравнения

- Перезапись, при необходимости, текущего кадра из второго буфера памяти в первый буфер памяти для использования его в дальнейшем в качестве опорного

Кратко рассмотрим суть данного способа.

Изображение рабочей поверхности, представленное на текущем кадре, сдвинуто по отношению к изображению, представленному на опорном кадре. Если сдвинуть текущий кадр по отношению к опорному на величину сдвига, то пересекающиеся части изображения должны совпасть. Поскольку кадры можно сдвигать на величину, кратную шагу дискретизации изображения (в данном случае он равен размеру оптической ячейки), точное совпадение получится только в том случае, если величина сдвига по обеим осям х, y кратна шагу дискретизации. Поэтому совмещение кадров ведется по методу наименьших квадратов. На каждом из кадров выбирается фрагмент изображения фиксированного размера М×М точек (далее - реперный модуль). На опорном кадре реперный модуль сдвинут относительно центра кадра на вектор R_r и представлен элементами A_r(i,j), а на текущем реперный модуль сдвинут на вектор R_c и представлен элементами A_c(i,j). Корреляционная функция f(R_r, R_c) определяется по формуле

Если вычислить корреляционную функцию f(R_r, R_c) для всех возможных значений R_r, R_c, то положение ее минимума соответствует наилучшей корреляции между опорным и текущим кадрами. Если минимуму f(R_r, R_c) соответствуют значения R_r=R1 и R_c=R2, то сдвиг между кадрами вычисляется по формуле:

R=R1-R2

Чтобы уменьшить объем вычислений, частоту кадров выбирают такой, чтобы за время одного кадра сдвиг по каждому из направлений не превышал ±1 шаг дискретизации. В этом случае, если известен результат предыдущего вычисления, то в текущем цикле вычислений необходимо вычислить только 9 значений корреляционной функции, соответствующих нулевому сдвигу и сдвигам на 1 шаг по 8 возможным направлениям по отношению к предыдущему сдвигу.

Когда сдвиг между опорным и текущим кадрами становится таким, что размер области пересечения кадров по одному из направлений меньше или равен размеру реперного модуля, возникает необходимость смены опорного кадра. В этом случае текущий кадр, хранящийся во втором буфере памяти, переписывается в первый буфер памяти и в дальнейшем используется в качестве опорного кадра. Для вычисления общего сдвига относительно исходного положения, к сдвигу, который далее будет вычисляться в соответствии с изложенным выше алгоритмом, добавляется сдвиг нового опорного кадра по отношению к первоначальному опорному кадру.

Очевидным недостатком данного способа вычисления сдвига является то, что разрешающая способность ограничена величиной шага дискретизации (размером ячейки фотоприемной матрицы). Если попытаться увеличить разрешение за счет уменьшения размера оптической ячейки, это приведет к пропорциональному уменьшению максимально допустимой скорости перемещения, так как максимально допустимый сдвиг за время одного кадра согласно условиям рассмотренного алгоритма не должен превышать ±1 шаг дискретизации.

Рассмотренный способ имеет также ограниченную интегральную точность вычислений. На каждом шаге вычислений ошибка равна ошибке округления. Среднеквадратичное значение ошибки округления по каждому направлению равно 1/. Суммарная ошибка по двум направлениям равна 1/. Если размер кадра равен N×N точек, максимально допустимый сдвиг между опорным кадром и текущим составляет S_max=N-M, после чего необходимо менять опорный кадр. Каждый раз при смене опорного кадра ошибка вычисления будет добавляться к уже накопленной ошибке. Таким образом, относительная ошибка вычислений по отношению к пройденному пути составляет 1/((N-M)·).

Наиболее существенным недостатком данного способа вычисления сдвига является неправильная работа алгоритма при пересечении ровной протяженной контрастной границы.

Протяженной - в данном случае означает, что длина границы превышает размер оптической матрицы.

Такая ситуация часто возникает, если рабочая поверхность представляет собой лист белой бумаги, на котором напечатан текст. Если оптический сенсор пересекает контрастную границу под прямым или близким к прямому углом с малой скоростью, рассмотренный алгоритм вычисления сдвига покажет, что сдвиг происходит вдоль границы, то есть в направлении, перпендикулярном к истинному направлению движения. Величина вычисленного сдвига при этом может во много раз превосходить истинное значение сдвига. Это обусловлено тем, что минимум корреляционной функции ищется не на всей области определения, а по дискретному набору точек. Поэтому вместо истинного минимума корреляционной функции находится условный минимум, положение которого может сильно искажать результат вычислений. Более подробно данный вопрос рассмотрен в разделе описания предлагаемого изобретения.

Известен способ вычисления сдвига, описанный в [3], в котором проблему повышения точности и разрешающей способности вычислений предлагается решать с помощью интерполяции. После вычисления корреляционной функции для 9 вариантов сдвига находятся промежуточные значения корреляционной функции, как среднее арифметическое близлежащих значений. Это позволяет удвоить разрешающую способность и точность вычислений. Однако для удвоения разрешающей способности количество обрабатываемых точек возрастает в 4 раза, то есть объем вычислений растет пропорционально квадрату разрешающей способности. Поэтому такой способ увеличения разрешающей способности не пригоден для создания прецизионных датчиков сдвига. Кроме того, никак не решается проблема контрастной границы, так как здесь по-прежнему при совмещении кадров и поиске минимума корреляционной функции используется дискретный набор возможных сдвигов.

То, что исходное изображение представлено дискретным набором точек, является принципиальным ограничением, приводящим к неправильной работе алгоритма при пересечении контрастной границы, что не позволяет обеспечить высокую точность вычислений на произвольных рабочих поверхностях.

Наиболее близким к предлагаемому способу вычисления сдвига является способ вычисления, описанный в [2].

Задачей настоящего изобретения является достижение технического результата, повышающего разрешающую способность и точность способа вычисления сдвига в датчике перемещения, а также расширение класса рабочих поверхностей, на которых возможна нормальная работа способа.

Для достижения названного технического результата в способе вычисления сдвига в датчике перемещения [2], включающем:

- формирование изображения рабочей поверхности, по которой движется датчик, в виде 2-мерной непрерывной картинки, описываемой функцией А(х,y), на поверхности фотоприемной оптической матрицы,

- дискретизацию сформированного изображения в пространстве и во времени и представление его в виде последовательности кадров, в каждом из которых исходное изображение представлено дискретным набором точек A_j,j,

- запоминание кадра, сформированного в первый момент времени в первом буфере памяти в качестве опорного кадра Aref_i,j,

- запоминание кадров, сформированных в последующие моменты времени, во втором буфере памяти в качестве текущего кадра Acur_i,j,

- вычисление сдвига между опорным и текущим кадрами путем их сравнения,

- перезапись, при необходимости, текущего кадра из второго буфера памяти в первый буфер памяти для использования его в дальнейшем в качестве опорного,

предложены следующие операции, являющиеся отличительными признаками предлагаемого способа вычисления сдвига:

- при формировании изображения поверхности, по которой движется датчик, устраняют компоненты изображения с пространственной длиной волны меньше удвоенного размера оптической ячейки,

- перед вычислением сдвига между опорным и текущим кадрами по дискретным наборам чисел Arefij и Acurij, хранящимся в первом и втором буферах памяти, восстанавливают исходные непрерывные функции Aref(x,y), Acur(x,y),

- вычисляют сдвиг между кадрами путем сравнения восстановленных непрерывных функций.

Проведенные патентные исследования показали, что в литературе отсутствует указание на использование вышеперечисленной совокупности отличительных признаков для повышения разрешающей способности и точности способа вычисления сдвига в датчике перемещения, а также расширения класса рабочих поверхностей, на которых возможна нормальная работа способа вычисления сдвига, что подтверждает новизну данного изобретения.

Рассмотрим более подробно суть предложенного способа.

Исходное изображение, спроектированное на поверхность фотоприемной матрицы, можно представить, как непрерывную 2-мерную функцию А(х,y). При преобразовании изображения в электрический сигнал с помощью оптической матрицы непрерывным координатам (х,у) ставится в соответствие дискретный набор точек (х_i,y_j). Точки (x_i,y_j) образуют координатную сетку, шаг которой - L равен размеру фотоячейки. Сигнал на выходе оптической матрицы представляет собой дискретный набор чисел A_i,j=A(x_i,y_j). Для того чтобы из дискретного набора значений A_i,j можно было восстановить исходную функцию А(х,y), функция А(х,y) должна удовлетворять условиям теоремы о дискретизации [4]. Если разложить функцию А(х,y) в ряд Фурье, длина волны самых коротковолновых компонентов ряда - λ_min должна удовлетворять условию:

λ_min>2·L,

Таким образом, для последующего восстановления исходной функции А(х,y) при формировании изображения необходимо обеспечить отсутствие в нем компонентов изображения с пространственной длиной волны меньше удвоенного размера оптической ячейки. Это можно обеспечить, например, расфокусировкой изображения так, чтобы размер пятна, соответствующего изображению точечного источника, был больше размера оптической ячейки.

Запоминание опорного и текущего кадров в первый и во второй буферы памяти соответственно происходит аналогично способу, рассмотренному выше [2]. Аналогично, вводится понятие реперных модулей и корреляционной функции. Далее, в нашем способе вычисления сдвига перед началом процедуры сравнения, т.е. поиска минимума корреляционной функции производится восстановление яркостных функций - А_r(х,y) и А_с(х,y), представляющих исходные изображения опорного и текущего кадров соответственно. Благодаря этому корреляционная функция становится определенной не на дискретном множестве точек, а на всей плоскости (х,y). Это дает возможность искать абсолютный минимум корреляционной функции, соответствующий максимально достоверному совмещению опорного и текущего кадров. Поскольку сдвиг реперных модулей при таком подходе может быть произвольным, а не кратным размеру решетки, разрешающая способность и точность вычисления сдвига ограничена только разрядностью представления данных. По этой же причине не возникает ошибок вычисления при пересечении контрастной границы.

Для увеличения вдвое разрешающей способности и точности вычисления в данном способе вычисления сдвига необходимо добавить 1 разряд в двоичном представлении исходных данных (т.е. увеличить на 1 разрядность АЦП) и в блоке вычисления. Это приводит к логарифмической зависимости роста аппаратных затрат от требуемой точности вычислений. Для сравнения, при использовании интерполяции в [3] для удвоения точности вычисления необходимо вчетверо увеличить количество точек изображения, что, в свою очередь, приводит к пропорциональному росту объема вычислений. Таким образом, в [3] рост аппаратных затрат от требуемой точности вычислений описывается квадратичной зависимостью. Поэтому очевидно, что по мере роста требований к точности и разрешающей способности датчиков перемещения, их стоимость при использовании предлагаемого способа будет существенно ниже.

Конкретный вариант реализации предлагаемого способа вычисления сдвига поясняется на фиг.1÷10.

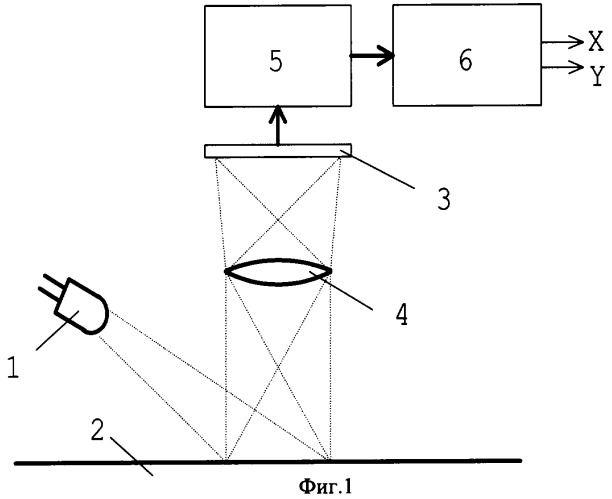
На фиг.1 показана структурная схема датчика перемещения.

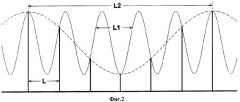
На фиг.2 показаны возможные искажения изображения при его дискретизации в оптической матрице без устранения компонентов изображения с пространственной длиной волны меньше удвоенного размера оптической ячейки.

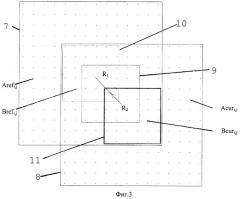
На фиг.3 поясняется способ совмещения кадров с помощью реперных модулей.

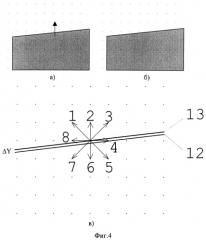
На фиг.4 поясняется причина неправильной работы способов вычисления сдвига с использованием дискретного представления кадра (в том числе [2], [3]) при пересечении контрастной границы.

На фиг.5 представлен результат работы способа вычисления сдвига с использованием дискретного представления кадра [3] при пересечении контрастной границы.

На фиг.6 поясняется способ восстановления непрерывной функции по набору дискретных значений.

На фиг.7 поясняется способ совмещения реперных модулей, когда сдвиг между опорным и текущим кадрами не превышает размера ячейки.

На фиг.8 поясняется способ совмещения реперных модулей для произвольной величины сдвига между опорным и текущим кадрами.

На фиг.9 представлена последовательность операций при вычислении сдвига предлагаемым способом.

На фиг.10 представлены сравнительные результаты вычисления траектории курсора при движении датчика по окружности для предлагаемого способа и для способа с использованием дискретного представления кадров [2].

Структурная схема датчика перемещения в конкретном варианте реализации изобретения приведена на фиг.1. Она содержит источник света 1, освещающий поверхность 2, по которой движется датчик, оптический матричный фотоприемник 3 форматом N×N фото ячеек (пусть для определенности N=18), оптическую систему 4, создающую изображение рабочей поверхности 2 на поверхности оптической матрицы 3, блок аналоговой обработки и преобразования 5, осуществляющий усиление сигнала оптической матрицы и преобразование его в цифровую форму, блок цифровой обработки 6, содержащий в своем составе память для хранения опорного и текущего кадров и специализированное вычислительное устройство для вычисления сдвига.

Шаг, с которым располагаются оптические ячейки в матрице по осям х и y, - L в дальнейшем для удобства примем за 1 длины. При проектировании изображения на поверхность оптической матрицы 3 его яркость описывается непрерывной функцией А(х,y). После преобразования изображения в оптической матрице в электрическую форму оно представляется дискретным набором точек A_i,j, образующих кадр. Чтобы при таком преобразовании не произошло потери информации, необходимо, чтобы размер самых мелких элементов изображения был больше L. При точной фокусировке это условие может не выполняться. Для того чтобы по дискретному набору точек можно было восстановить исходное изображение, необходимо расфокусировать оптическую систему 4, так чтобы точечному объекту на рабочей поверхности 2 соответствовало пятно на поверхности оптической матрицы 4 с размером, большим или равным L. Если это условие не выполнено, в процессе дискретизации изображения могут произойти искажения, которые в дальнейшем приводят к ошибкам и не могут быть исправлены.

Эта ситуация поясняется на фиг.2. Изображение имеет пространственную длину волны L1, что соответствует пространственной частоте 1/L1. Поскольку L1 не удовлетворяет условию L1>2·L, после дискретизации изображения в оптической матрице образуются компоненты с пространственной длиной волны L2, которая определяется уравнением:

1/L2=1/L-1/L1.

При этом величина L2 может быть значительно больше, чем L1. Если картинка на поверхности оптической матрицы сдвигается на L1, то на выходе оптической матрицы дискретизированное изображение сдвинется на L2>>L1. Таким образом, сдвиг, который покажет любой способ вычисления сдвига, будет значительно больше реального смещения.

Расфокусировка оптической системы играет роль фильтра нижних частот, устраняющего компоненты изображения с пространственными частотами выше 1/(2·L). Это гарантирует, что после дискретизации изображения в оптической матрице по дискретному набору точек может быть восстановлено исходное непрерывное изображение. При практической реализации предлагаемого способа вычисления сдвига сигнал с выхода оптической матрицы необходимо дополнительно пропустить через полосовой фильтр. Эта необходимость продиктована двумя обстоятельствами.

Во-первых, осветитель 1 (фиг.1) дает, как правило, неравномерную освещенность поверхности 2. Поскольку осветитель движется вместе с датчиком, яркость кадра в центре всегда отличается от яркости на краях. Неравномерность освещенности воспринимается при сравнении кадров как элемент изображения, который всегда стоит на месте. Если контрастность элементов изображения поверхности в кадре меньше или сравнима с неравномерностью освещенности, способ вычисления сдвига может давать большую ошибку. Чтобы устранить эту проблему, необходимо отфильтровать элементы изображения, сравнимые с размером матрицы.

Во-вторых, на выходе блока аналоговой обработки 5 (фиг.1) наряду с полезным сигналом присутствует шум. Это также может привести к ошибкам при сравнении кадров. Как будет показано ниже, при сравнении кадров для восстановления исходного изображения необходимо вычислять производные по координатам. При вычислении производных наибольший вклад в ошибку вычислений дают коротковолновые компоненты шума. Поэтому требуется дополнительная фильтрация коротковолновых компонентов изображения.

Совместить перечисленные выше два требования можно, пропустив сформированный блоком 5 кадр через полосовой фильтр. В качестве примера конкретного исполнения можно использовать 2-мерный FIR-фильтр с матрицей коэффициентов размером 5×5. Параметры фильтра задаются набором коэффициентов F_k,m; k, m=(-2÷2). Сигнал на выходе фильтра - Af_i,j вычисляется из входного сигнала - A_i,j по общепринятой формуле для фильтров [5]

Если размер кадра на входе фильтра равен N×N, то размер кадра на выходе фильтра уменьшается до (N-4)×(N-4). Поскольку размер кадра на выходе фильтра меньше, чем на входе, для экономии памяти в память записывается кадр с выхода фильтра. Поэтому далее каждый раз, когда идет речь о запоминании или обработке кадра, имеется в виду кадр с выхода полосового фильтра. Учитывая, что исходный размер кадра был выбран 18×18, размер кадра в дальнейшем в процессе обработки будет равен 14×14 точек.

Для того чтобы вычислить сдвиг датчика за какое-то время, необходимо сравнить кадр, сделанный в начальный момент времени, и кадр, сделанный в текущий момент времени. Кадр, сделанный в начальный момент времени, записывается в первый буфер памяти и хранится там в качестве опорного кадра. Кадр, сделанный в следующий момент времени за опорным, записывается во второй буфер памяти и используется в качестве текущего кадра. Текущий кадр сравнивается с опорным, и вычисляется величина сдвига между ними. Затем во второй буфер записывается следующий кадр и повторяется процедура вычисления сдвига. Когда сдвиг между опорным и текущим кадрами становится настолько большим, что дальнейшее их сравнение становится невозможно, текущий кадр переписывается из второго буфера памяти в первый буфер памяти и далее используется в качестве опорного. Далее сдвиг текущего кадра вычисляется относительно нового опорного кадра. Суммарный сдвиг текущего кадра равен сумме текущего вычисленного сдвига и сдвига нового опорного кадра относительно первоначального опорного кадра. Каждый раз при смене опорного кадра увеличивается суммарная погрешность вычисления общего сдвига. Поэтому для минимизации погрешности алгоритма необходимо как можно реже менять опорный кадр.

Способ совмещения опорного и текущего кадров поясняется на фиг.3. Рассмотрим сначала более простой случай, когда сдвиг в каждом из направлений кратен целому количеству L. Если текущий кадр 8 сдвинут относительно опорного кадра 7, то в области их пересечения изображения должны совпадать. Выберем в области пересечения фрагмент 9 размером М×М точек (пусть для определенности М=6), который в дальнейшем будем называть реперным модулем. Реперный модуль выделяет на опорном кадре фрагмент Bref_i,j, который сдвинут по отношению к центральному положению 10 на вектор R₁, а на текущем кадре фрагмент Bcur_i,j, который сдвинут по отношению к центральному положению 11 на вектор R₂. Корреляционную функцию определим в соответствии с методом наименьших квадратов выражением

Минимум корреляционной функции соответствует положению реперных модулей, при котором опорный и текущий кадр совмещены наилучшим образом. Если найдены векторы R₁, R₂, соответствующие минимуму корреляционной функции, то сдвиг между кадрами вычисляется по формуле

D=R₁-R₂.

Корреляционная функция легко вычисляется для R₁, R₂ кратных L. В известных способах вычисления сдвига реперные модули сдвигаются в каждом из направлений на целое количество периодов решетки L, и минимум корреляционной функции ищется при условии, что векторы R₁, R₂ в каждом из направлений кратны величине L, или если принять L=1, векторы R₁, R₂ - имеют целочисленные значения. Помимо ограниченной точности, такой подход ведет к неправильной работе алгоритма при пересечении контрастной ровной границы. Эта ситуация поясняется на фиг.4.

На фиг.4а показан опорный кадр, а на фиг.4б - текущий. За время одного кадра происходит небольшой сдвиг границы раздела между черной и белой областями вверх. На фиг.4в показано положение границы раздела на опорном кадре 12 и на текущем 13, из которого видно, что граница раздела сдвинулась вверх на величину ΔY. Для того чтобы наилучшим образом совместить кадры, текущий кадр необходимо сдвинуть вниз в направлении 6 на величину ΔY<<1. Если алгоритм совмещения кадров не допускает дробный сдвиг, то из 8 возможных направлений сдвига, показанных на фиг.4, алгоритм выберет сдвиг в направлении 4, так как именно в этом направлении получается наилучшее совмещение границ раздела. При этом мелкие, малоконтрастные фрагменты кадров не совместятся. Однако их вклад в корреляционную функцию гораздо меньше, чем вклад контрастной границы. Таким образом, вычисленное значение сдвига по величине и направлению сильно отличается от истинного сдвига. Возникает эффект скольжения вдоль контрастной границы.

Этот эффект хорошо виден на фиг.5, где показан пример как влияет дискретное перемещение реперных модулей при совмещении кадров на результат вычисления сдвига. Датчик перемещения движется по дуге окружности 14, а вычисленная траектория проходит по кривой 15. Скорость движения датчика составляет 0.005 ячеек/кадр. Уменьшение шага решетки путем уменьшения размера ячейки или с помощью интерполяции принципиально не устраняет данного эффекта. Оно только изменяет масштаб скорости, при которой эффект проявляется максимально сильно.

Чтобы устранить указанный эффект, необходимо при поиске минимума корреляционной функции допустить сдвиг реперных модулей 10,11 (фиг.3) на произвольную величину, включая дробное значение. Для этого необходимо по дискретным наборам данных Aref_i,j, Acur_i,j, представляющих опорный и текущий кадр соответственно, восстановить непрерывные функции Aref(x,y), Acur(x,y).

Способ восстановления поясняется на фиг.6. Для восстановления функции А(х,y) в окрестности точки (х_i, y_j) используются 9 ближайших значений из дискретного набора, а именно: A_i+kj+m (k, m=-1, 0, +1). Значения функции А(х,у) аппроксимируются полиномом 2-го порядка:

Аппроксимация производится методом наименьших квадратов. Сумма квадратов разностей между значениями функции А(х,у) в 9-ти указанных выше точках (см. фиг.6) и значениями A_i+kj+m (k, m=-1, 0, +1) должна быть минимальна. Это означает, что необходимо найти минимум функции

Прежде, чем подставлять в уравнение (2) значения А(х_i+k, y_j+m) из уравнения (1), необходимо отметить, что (х_i+k-x_i)=k, a (y_j+m-y_j)=m, так как размер ячейки L принят за 1. Тогда для F имеем уравнение.

Чтобы найти минимум функции F, необходимо продифференцировать уравнение (3) по переменным A₀, А_х, А_у, A_xx, A_yy, A_xy и приравнять производные нулю. После дифференцирования получаем линейную систему 6-ти уравнений с 6-ю неизвестными:

После выполнения суммирования система (4)÷(9) преобразуется к виду:

Решение системы (10)÷(15) записывается в виде:

где введены следующие обозначения:

Таким образом, уравнения (1), (16)÷(27) позволяют аппроксимировать функцию А(х,y) в окрестности любой точки (х_i, y_j), кроме крайних точек, находящихся на периферии кадра. Следовательно, восстановленный кадр А(х,y) имеет размер 12×12 точек. Операция восстановления заключается в вычислении для каждой точки (х_i,y_j) исходного кадра чисел A₀(i,j), A_x(i,j), A_y(i,j) по формулам (16)÷(18), (22)÷(24). Коэффициенты A_xx(i, j), A_yy(i, j), A_xy(i, j), как будет показано дальше, для дальнейших вычислений не потребуются, и поэтому не вычисляются. Поскольку аппроксимация производится по 8-ми точкам из ближайшего окружения точки (х_i, y_j), полученные выражения справедливы в окрестности±1 относительно точки (х_i, y_j) в каждом направлении, то есть внутри области 16, показанной на фиг.6 пунктирной линией.

В уравнении (1) для аппроксимации функции А(х,y) используется многочлен второго порядка. Для повышения точности восстановления функции А(х,y) можно использовать многочлен более высокого порядка. Это приведет к увеличению количества коэффициентов в уравнении (1). В итоге придется решать линейную систему уравнений более высокого порядка. Однако, если сигнал с выхода оптической матрицы помимо полезного сигнала содержит шум, повышение порядка аппроксимирующего многочлена может понизить точность вычисления сдвига. Это связано с тем, что аппроксимирующий многочлен играет роль фильтра, который ослабляет шум. Чем выше порядок многочлена, тем меньше ослабляется шум. Поэтому в данном варианте реализации способа вычисления сдвига используется второй порядок аппроксимации.

Следующим шагом в вычислении сдвига является совмещение реперных модулей на опорном и текущем кадре. Для того чтобы существенно сузить область поиска при совмещении реперных модулей, частота кадров - F_FR выбирается таким образом, чтобы при максимальной скорости движения датчика - V_max величина сдвига между двумя соседними кадрами не превышала в каждом из направлений - х, у размера оптической ячейки - L. В частности, если максимальную скорость перемещения датчика положить равной V_max=1 м/с, а размер ячейки L=50 мкм, частота кадров должна составлять F_FR=20 кГц. Это ограничение не является принципиальным для реализации рассматриваемого способа вычисления сдвига, однако оно позволяет значительно сократить объем вычислений, что ведет к экономии размера и стоимости устройства в рассматриваемом варианте исполнения. При выполнении указанного условия первый текущий кадр, записанный сразу после записи опорного кадра, будет сдвинут по отношению к опорному на расстояние, не превышающее по каждой из координат размер ячейки.

Эта ситуация поясняется на фиг.7. Здесь опорный кадр представлен набором точек 17, а текущий кадр - набором точек 18. Текущий кадр сдвинут по отношению к опорному на вектор ΔR=(Δх,Δy), где Δх<1, Δy<1. Для совмещения реперных модулей реперный модуль на опорном кадре необходимо сдвинуть на вектор ΔR/2=(Δх/2, Δy/2), а на текущем кадре реперный модуль необходимо сдвинуть на вектор -ΔR/2=(-Δx/2, -Δy/2).

Исходный, не сдвинутый реперный модуль на опорном кадре (поз.10 на фиг.3) представлен набором чисел Bref_i,j (i, j=1÷6). Если реперный модуль сдвигается на (Δх/2, Δy/2), новые значения Bref_i,j (Δх, Δy) могут быть выражены через значения восстановленных функций яркости, соответствующим точкам (х_i, y_j), входящим в состав не сдвинутого реперного модуля. Они могут быть записаны с помощью уравнения (1). Поскольку сдвиг по каждой из координат не превышает ½, в уравнении (1) можно оставить только линейные члены. Это приводит к выражению для сдвинутого реперного модуля:

Аналогично для сдвинутого реперного модуля на текущем кадре можно записать

Корреляционная функция, как отмечалось выше, определяется выражением:

С учетом (28), (29) уравнение (30) перепишется в виде:

Чтобы совместить реперные модули, необходимо найти минимум корреляционной функции по переменным Δх, Δy, то есть уравнение (31) необходимо продифференцировать по Δх, Δy и приравнять производные нулю. При этом получается линейная система 2-х уравнений относительно Δх, Δy:

Система (32), (33) приводится к нормальному виду:

где введены следующие обозначения:

Решение системы (34), (35) записывается в виде:

Уравнения (36)÷(42) позволяют вычислить сдвиг между опорным и текущим кадрами, когда величина сдвига каждого реперного модуля не превышает по каждой из координат ±1, то есть, если суммарный сдвиг по каждому направлению не превышает ±2. Как отмечалось ранее, в начальный момент времени это условие выполняется, если скорость датчика не превышает максимально допустимого значения.

Дальнейшая процедура вычисления для произвольной величины сдвига поясняется на фиг.8. Здесь опорный кадр представлен набором точек 19, а текущий кадр - набором точек 20. Центр опорного кадра расположен в точке А, центр текущего кадра - в точке D. Сдвиг, который предстоит вычислить, равен вектору AD. Из предыдущего цикла вычислений известно, что сдвиг был равен АВ. Так как за время одного кадра сдвиг не превышает 1, длина вектора BD не превышает 1 в каждом из направлений. Если компоненты вектора АВ округлить до ближайших целых значений, получится вектор АС. Суть предлагаемого способа вычисления заключается в том, что известная заранее целочисленная часть сдвига АС компенсируется сдвигом реперных модулей на целое количество шагов решетки, а оставшаяся дробная часть CD вычисляется. Поскольку длина вектора СВ по каждому из направлений не превышает 0.5 согласно правилам округления, а длина вектора BD не превышает по каждому из направлений 1, длина суммарного вектора CD по каждому из направлений не превышает 1.5, что позволяет использовать уравнения (36)÷(42) для его вычисления. Для вычисления вектора AD необходимо выполнить следующую последовательность действий.

- Округлить до ближайшего целого значения компоненты вектора АВ. Получаем вектор АС, равный округленному значению суммарного сдвига, вычисленного в предыдущем кадре.

- Делим вектор АС пополам и округляем его компоненты до целого в большую сторону. Получаем вектор АЕ. Сдвигаем реперный модуль в опорном кадре на вектор АЕ.

- Вычисляем вектор DF по формуле: DF=AE-АС. Поскольку компоненты векторов АЕ и АС - целые, компоненты вектора DF - тоже целые. Сдвигаем реперный модуль на текущем кадре на вектор DF.

- Совмещаем реперные модули в точке G и вычисляем вектор EF с помощью уравнений (36)÷(42).

- Вычисляем вектор AD по формуле: AD=AC+EF.

Поскольку размер реперного модуля в рассматриваемом примере исполнения равен 6×6, а размер кадра после восстановления непрерывной функции А(х,у) равен 12×12, максимально допустимая целочисленная величина сдвига межд