Устройство для измерения характеристик светорассеяния оптико-электронных приборов

Устройство для измерения характеристик светорассеяния оптико-электронных приборов

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерений характеристик светорассеяния оптико-электронных приборов (ОЭП) и может быть использовано в технике экспериментального измерения индикатрисы отражения, пеленгационной характеристики и эффективной площади рассеяния ОЭП в лабораторных условиях.

Известно, что для сравнительной оценки световозвращательной способности различных ОЭП используются основные световозвращательные характеристики. К ним относятся [ЛАЗЕР-ИНФОРМ. Информационный бюллетень Лазерной ассоциации №4 (259) февраль, 2003, Н.В.Барышников, к.т.н., В.Е.Карасик, д.т.н., проф., МГТУ им.Н.Э.Баумана, Москва, 7 мая 2003 г]:

- эффективная площадь рассеяния (ЭПР) - σ;

- индикатриса отражения;

- пеленгационная характеристика.

Совокупность ЭПР по всем направлениям относительно оптической оси световозвращателя составляет его пространственную индикатрису отражения.

Пеленгационной характеристикой ОЭП - σ(j) называют зависимость ЭПР от угла пеленга j - угла между осью оптической системы ОЭП и направлением на источник подсвета.

При этом известно, что в ходе процессов локации и измерении характеристик светорассеяния ОЭП, как правило, используются лазерные пучки [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.], а расстояния между источником и ОЭП, и приемником и ОЭП могут не совпадать [патент RU №2256871, 2003 г.]

Известно устройство для определения эффективной площади рассеяния ОЭП (см., например, патент RU №2284486, по классу G01J 1/10, 2006 г.), включающее расположенные по ходу зондирующего излучения лазер подсвета и светорасщепитель, между которыми последовательно установлены по ходу зондирующего лазерного излучения коллиматор и объектив, с фокусным расстоянием f, равным удвоенному расстоянию между светорасщепителем и держателем исследуемого ОЭП, между светорасщепителем и фотоприемником по ходу ответвленного светорасщепителем отраженного от ОЭП средства излучения.

Недостатком данного устройства является большая систематическая погрешность измерений значений ЭПР, обусловленная реализацией посредством этого устройства метода локации в сходящемся пучке.

Проведем оценку систематической погрешности измерений, возникающей при использовании описанного выше устройства. Согласно [Ю.Л.Козирацкий, В.Д.Попело, Методы экспериментального исследования характеристик отражения оптико-электронных средств, Научно-методические материалы, 5 ЦНИИИ МО РФ, 1998 г. 186 с. (стр.120)]:

расстояние между входным зрачком ОЭП и объективом равно L=0,5f;

диафрагма устанавливается в плоскости анализа отраженного от ОЭП излучения, удаленной от входного зрачка ОЭП на расстояние, также равное L=0,5f.

При этом радиус отверстия диафрагмы rd зависит от моделируемой трассы локации Lm и определяется с помощью следующего выражения:

,

где: ro - радиус входного зрачка приемного канала реального образца лазерного локатора.

Известно, что отношение мощностей принимаемого расположенным за диафрагмой приемником излучения, проходящего через отверстия с одинаковыми значениями их радиусов, пропорционально отношению плотности мощности в плоскости этих отверстий. В свою очередь плотность мощности в сходящемся пучке зависит от удаления плоскости анализа относительно его перетяжки (точки его фокусировки), а отношение плотностей мощности равно отношению квадратов радиусов пучков в плоскости анализа, которые зависят от удаления плоскости анализа от перетяжки.

Определим удаление перетяжки отраженного от ОЭП сходящегося пучка.

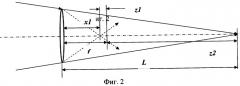
Рассмотрим ход проходящих в прямом направлении лучей при локации оптико-электронных средств (ОЭП) в сходящемся пучке, который показан на Фиг.2.

На Фиг.2 приведены следующие обозначения: L - радиус кривизны волнового фронта в плоскости входного зрачка ОЭП (дальность локации ОЭП в сходящемся пучке); f - значение параксиального фокуса объектива ОЭП; x1 - расстояние между задней главной плоскостью объектива ОЭП и точкой пересечения сфокусированного им сходящегося пучка с осью; z1 - расстояние между параксиальным фокусом объектива и точкой пересечения сфокусированного им сходящегося пучка с оптической осью; z2 - расстояние между параксиальным фокусом объектива и точкой пересечения направлений лучей падающего на входной зрачок пучка с оптической осью.

Значение расстояния между задней главной плоскостью объектива ОЭП и точкой пересечения сфокусированного им сходящегося пучка x1 может быть определено с помощью уравнения Гаусса [Прикладная оптика / Дубовик А.С.и др.; Учебное пособие для вузов, М., Недра, 1982, 621 с. (стр.40-41)]:

.

Из Фиг.2 следует, что расстояние между параксиальным фокусом объектива и точкой пересечения направлений лучей падающего на входной зрачок пучка с осью z2 равно:

.

Подставляя (3) в (2) после простых преобразований и сокращений получим:

.

Из (4) видно, что значение х1 меньше значения параксиального фокуса объектива ОЭП.

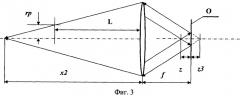
На Фиг.3 приведен ход проходящих в прямом и обратном направлениях лучей при локации оптико-электронных средств (ОЭП) в сходящемся пучке.

На Фиг.3 приняты следующие обозначения: ОП - отражающая плоская поверхность, расположенная в параксиальной фокальной плоскости объектива перпендикулярно его оптической оси; х2 - расстояние между передней главной плоскостью объектива и точкой пересечения лучей отраженного им сходящегося пучка излучения; z3 - расстояние между отражающей поверхностью и точкой пересечения продолжения отраженных ОП лучей.

Из Фиг.2 и 3 и геометрических соображений следует:

;

поскольку углы падения и отражения лучей относительно ОП равны, то и равны значения расстояний между параксиальным фокусом объектива и точкой пересечения сфокусированного им сходящегося пучка с оптической осью z1 и между отражающей поверхностью и точкой пересечения продолжения отраженных ОП лучей z3;

отраженный от ОП пучок лучей может быть заменен на эквивалентный гомоцентрический пучок, точка излучения которого находится на оптической оси и удалена от ОП на расстояние z3.

С учетом изложенного выше значение расстояния между передней главной плоскостью объектива ОЭП и точкой пересечения сфокусированного им отраженного от ОП сходящегося пучка х2 как эквивалентного гомоцентрического пучка может быть определено с помощью уравнения Гаусса [Прикладная оптика / Дубовик А.С.и др.; Учебное пособие для вузов, М., Недра, 1982, 621 с. (стр.40-41)]:

.

Последовательно подставляя (6) в (5) и (4) и производя последовательные преобразования и сокращения, получим:

.

Из приведенных выше рассуждений и выражения (7) следует, что систематическая погрешность измерений, возникающая при использовании описанного выше устройства, вызвана установкой диафрагмы в заявленном устройстве (смещением плоскости анализа) относительно плоскости перетяжки отраженного от ОЭП сходящегося пучка на расстояние, равное 2f.

Из Фиг.2 и выражения (7) следует, что значение радиуса пучка в плоскости, удаленной от передней главной плоскости объектива на расстояние L, может быть определено с помощью следующего выражения:

,

где r_ОЭП - радиус входного зрачка лоцируемого ОЭП.

Принимая, что радиус пучка в плоскости, удаленной от ОЭП на расстояние, равное 2f+L, равен радиусу диафрагмы, с учетом (7) и (8) можно получить следующее выражение, позволяющее получить значение отношения мощностей сигналов К, регистрируемых после диафрагмы, находящейся от объектива на расстоянии 2f+L и L соответственно:

.

Пусть Lm=3 км, r_ОЭП=ro=3 см, L=1 м, а f=10 см.

Проведенные с помощью выражения (9) расчеты показали, что в этом случае К=9·10⁶. То есть измерение ЭПР в сходящемся пучке в рассмотренном случае приводит к занижению истинного значения ЭПР почти на семь порядков.

Изложенное выше показывает, что использование устройства по патенту RU 2284486 C1 no классу G01J 1/10 приводит к систематическим ошибкам измерения значений ЭПР ОЭП на несколько порядков.

Известно устройство для определения эффективной площади рассеяния ОЭП (см., например, Майзельс Е.Н., Торгованов В.А, Измерение характеристик рассеяния радиолокационных целей. - М.: Советское радио, 1972, с.41), включающее лазер подсвета, держатель исследуемого ОЭП, установленные по ходу зондирующего лазерного излучения, фотоприемник, установленный по ходу отраженного от ОЭП лазерного излучения, и регистратор выходного сигнала фотоприемника, вход которого подключен к выходу фотоприемника.

Недостатками данного устройства являются наличие систематической погрешности измерений, связанной с малой длиной измерительной трассы (ограниченной длиной лабораторного помещения), а также невозможность измерения данным устройством индикатрис отражения ОЭП.

Так известно, что наиболее распространенным и простым способом измерения значений ЭПР ОЭП является способ прямых измерений, основанный на регистрации величины напряжения на выходе приемного канала измерителя U₀, пропорционального уровню отраженного от ОЭП сигнала излучения в плоскости его приема. Измерения проводятся с помощью предварительно прокалиброванной с использованием ЭС аппаратуры. Уравнение прямых измерений имеет следующий вид:

σ=g_ЭU₀,

где g_э - цена деления шкалы измерительного устройства.

Наиболее распространенным способом калибровки является градуировка измерительной аппаратуры по эталонному отражателю, размещаемому на той же дальности, что и исследуемое ОЭП. При условии линейности рабочей характеристики измерительного тракта аппаратуры значение g_Э определяется как:

,

где σ_Э - ЭПР ЭС (ЭС), U_э - величина сигнала, пропорционального уровню отраженного от ЭС излучения в плоскости его приема.

Как правило, при проведении калибровки в качестве ЭС используются сферические выпуклые зеркала с известными значениями радиуса кривизны R_з и коэффициента отражения р_з зеркальной поверхности. При этом значения R_з колеблются в пределах единиц - десятков метров, а значения р_з от 0.8 до 0,95. В [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.] показано, что значение ЭПР такого ЭС может быть рассчитано с помощью следующего выражения:

Из выражения (10) следует, что ЭПР сферического выпуклого зеркала зависит только от параметров, характеризующих это зеркало.

Однако результаты экспериментальных исследований показали, что выражение (10) для расчета ЭПР сферического выпуклого зеркала как ЭС при проведении калибровки измерительной аппаратуры на трассах ограниченной протяженности (особенно в лабораторных условиях) не справедливо, что приводит к погрешности калибровки измерителя ЭПР и, следовательно, к систематическим погрешностям измерения ЭПР реальных образцов ОЭП.

Этот факт был обнаружен в ходе сопоставления результатов измерения ЭС с известными значениями ЭПР и объясняется тем, что значения ЭПР эталонных отражателей зависят от условий их локации, которые при выводе выражения (10) в [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.] не учитывались. Под условиями локации в рассматриваемом случае понимаются параметры, характеризующие:

расстояние между ЭС и источником зондирующего излучения;

расстояние между ЭС и входным зрачком приемного канала измерительной аппаратуры.

Известно, что условию облучению ЭС лазером без коллиматора на его выходе соответствует расходящийся пучок.

В дальнейшем будем считать, что в этом случае источник облучения является точечным и расходящимся.

Вывод выражения (10) для точечного источника приведен, например, в [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.], где было показано, что если известна сила излучения источника зондирующего излучения (ЗИ) (облучателя цели) I_изи, то величина лучистого потока, который достигнет входного зрачка приемного канала измерителя после отражения от объекта сферической формы с зеркальной поверхностью, будет определяться следующим выражением:

.

где: S_п - площадь отражающей круглой площадки на поверхности ЭС, от которой отраженное излучение будет попадать во входной зрачок приемного канала измерителя; L - дальность локации; τ_с - коэффициент пропускания зондирующего излучения на трассе длиной L.

.

где: r - радиус площадки на поверхности ЭС, от которой отраженное излучение будет попадать во входной зрачок приемного устройства;

D - диаметр входного зрачка объектива приемного канала измерителя.

При выводе выражений (10), (11) и (12) предполагалось следующее:

- источник ЗИ является точечным;

- центр точечного источника ЗИ совпадает с центром входного зрачка объектива приемного канала локатора;

- расстояния от центра ЭС до источника и от центра ЭС до центра входного зрачка объектива приемного канала равны;

- оптические оси пучка ЗИ и оптического тракта приемного канала совпадают и проходят через центр ЭС;

- диаметр пучка отраженного от ЭС излучения меньше, чем диаметр входного зрачка приемного канала (ПК);

- поперечные размеры сформированного отраженным от ЭС излучением пятна на фоточувствительной поверхности приемника меньше поперечных размеров этой поверхности;

- радиус кривизны ЭС значительно меньше дальности локации.

Однако, как показали предварительные оценки, последнее условие на трассах локации ограниченной протяженности (особенно в лабораторных условиях) практически не выполняется.

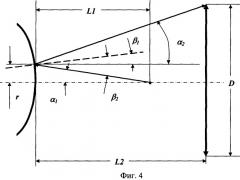
Для оценки влияния соотношения между радиусом кривизны ЭС и дальностью локации на значение ЭПР ЭС рассмотрим процессы облучения ЭС и отражения от него излучения точечного источника ЗИ (Фиг.4).

На Фиг.4 обозначено: α1 - угол между оптической осью приемного канала (ПК) и направлением распространения луча от источника ЗИ, попадающего после отражения от ЭС на край входного зрачка объектива ПК (далее крайнего луча); α2 - угол между направлением распространения крайнего луча после отражения от ЭС и оптической осью ПК; β1 - угол между нормалью к ЭС в точке отражения крайнего луча и оптической осью ПК; β2 - угол между нормалью к ЭС в точке отражения крайнего луча и падающим в эту точку лучом; L1 - расстояние между источником и точкой ЭС, расположенной на оптической оси ПК; L2 - расстояние между точкой ЭС, расположенной на оптической оси ПК и плоскостью входного зрачка объектива ПК.

Пусть, как и в [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.] точечный источник ЗИ находится на оптической оси ПК, и оптическая ось пучка совпадает с оптической осью ПК. В этом случае, как это следует из фигуры 3, угол α2 равен:

.

Выражение (13) отличается от выражения для угла α2, полученного в [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.], наличием в числителе вычитаемого, равного 2r. В то же время из фигуры 3 следует, что:

α2=β1+β2 и β2=β1+α1

откуда: .

Поскольку L1 много больше r, то α1=r/L1, откуда:

.

Подставляя (15) в (13) и принимая, что поскольку радиус кривизны сферического выпуклого зеркала много больше радиуса площадки на поверхности ЭС, от которой отраженное излучение будет попадать во входной зрачок приемного устройства r, то β1=r/R_з. В этом случае получим, что при L1≠L2 радиус г будет равен:

.

При преобразуется к следующему виду:

.

Площади отражающей круглой площадки на поверхности ЭС, от которой отраженное излучение будет попадать во входной зрачок приемного устройства, для различных условий локации ЭС точечным источником будут соответственно равны:

.

Известно, что, уровень сигнала, снимаемого с фотоприемника ПК локатора, прямо пропорционален облученности его входного зрачка, которая напрямую зависит от ЭПР ЭС. Поскольку во входной зрачок объектива ПК попадает только та часть ЗИ, которая отражается от круглой площадки на поверхности ЭС радиусом r, то отношение облученности в плоскости этого объектива, рассчитанной с помощью выражений (18) H(L1≠L2) или (19) H(L1=L2=L), к облученности, рассчитанной с помощью известного выражения (12) Н₃, будут соответственно равны:

,

.

В таблице 1 приведены рассчитанные с помощью выражений (20) и (21) отношения ПСВ ЭС для различных дальностей локации и значений радиуса кривизны отражающей поверхности ЭС.

Таблица 1
Отношения ПСВ ЭС для различных дальностей локации и значений радиуса кривизны отражающей поверхности ЭС при его облучении точечным источником.
L1, м	10 (лаб. усл.)	20	50	100	200	500	750	1000	1500
К1, R3=5 м L2=0,5L1	0,327	0,529	0,756	0,865	0,929	0,971	0,98	0,985	0,99
К1, R3=10 м L2=0,5L1	0,16	0,327	0,592	0,756	0,865	0,943	0,961	0,971	0,98
К1, R3=15 м L2=0,5L1	0,095	0,221	0,476	0,666	0,808	0,916	0,943	0,956	0,971
К2, R3=5 м	0,44	0,64	0,826	0,907	0,952	0,98	0,987	0,99	0,993
К2, R3=10 м	0,25	0,444	0,694	0,826	0,907	0,961	0,974	0,98	0,987
К2, R3=15 м	0,16	0,327	0,592	0,756	0,865	0,943	0,961	0,971	0,98

Из таблицы 1 и выражений (20) и (21) следует, что:

текущее значение ПСВ ЭС при дальностях локации, соизмеримых с радиусом кривизны отражающей поверхности, будет в несколько раз меньше значения ПСВ, рассчитанного с помощью известного выражения (10), что приведет к аналогичному завышению значений ЭПР ОЭП при измерениях прокалиброванной с помощью таких ЭС аппаратуры;

только при дальности локации L, превосходящей радиус кривизны ЭС R₃ более чем на два порядка, отношения измеренных значений ПСВ К1 и К2 становятся примерно равными единице.

Поскольку в известном устройстве для определения эффективной площади рассеяния ОЭП [Майзельс Е.Н., Торгованов В.А. Измерение характеристик рассеяния радиолокационных целей. - М.: Советское радио, 1972, с.41] отсутствуют элементы перемещения фотоприемника относительно оптической оси отраженного от ОЭП пучка зондирующего излучения и регистрации значений углов между направлением на приемник относительно центра входного зрачка ОЭП и оптической осью ОЭП, то индикатрису отражения ОЭП данным устройством нельзя.

Таким образом, применение известного устройства для определения эффективной площади рассеяния ОЭП [Майзельс Е.Н., Торгованов В.А. Измерение характеристик рассеяния радиолокационных целей. - М.: Советское радио, 1972, с.41] не учитывает зависимости значений ЭПР эталонных сферических отражателей от дальности, что приводит к занижению измеренных значений ЭПР ОЭП до шести раз, а также не обеспечивает возможность измерения данным устройством индикатрисы отражения ОЭП.

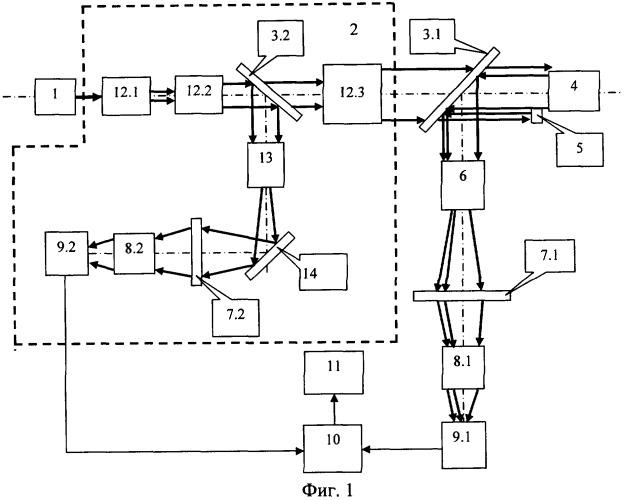
Наиболее близким по технической сущности и достигаемому результату является устройство для измерения показателя световозвращения оптико-электронных приборов [Россия, Патент №2202814 по классу G02В 23/12, 2003 г.], которое включает источник излучения и последовательно установленные по ходу его излучения формирующую оптическую систему, установленные с возможностью замены оптико-электронный или оптический приборы и эталонный световозвращатель, первый светоделитель, приемный коллиматор, второй светоделитель, в одном плече которого установлена проекционная система и матрица ПЗС, плоскость установки которой оптически сопряжена с фокальной плоскостью приемного коллиматора, а в другом плече - конденсорная линза и приемник излучения, выход которого сопряжен со входом цифрового вольтметра, выходы матрицы и цифрового вольтметра соединены со входом микропроцессора, выход которого соединен с монитором, при этом микропроцессор выполнен с возможностью регулирования измерительного телесного угла усреднения Ω_изм в соответствии с величиной измеряемого показателя световозвращения и телесного угла усреднения Ω_эт, соответствующего индикатрисе отражения от эталонного световозврвщателя, а также вычисления значения показателя R_св световозвращения инспектируемого световозвращателя, усредненного в телесном угле Ω_изм по выражению

где Uсв^max напряжение сигнала, снимаемого с приемника излучения при регистрации излучения, отраженного от инспектируемого световозвращателя, и вычисленное микропроцессором в телесном усреднения Ω_изм;

U_эт ^max - напряжение сигнала, снимаемого с приемника излучения при регистрации излучения, отраженного от ЭС, и вычисленное микропроцессором в телесном угле усреднения Ω_эт;

Ф_св( Ω_изм) - поток, падающий на матрицу ПЗС при регистрации излучения, отраженного от инспектируемого световозвращателя, и вычисленный микропроцессором в телесном угле усреднения Ω_изм;

Ф_СВ( Ω_эт) - поток, падающий на матрицу ПЗС при регистрации излучения, отраженного от инспектируемого световозвращателя, и вычисленный микропроцессором в телесном угле усреднения Ω_эт;

R_эт - показатель световозвращения ЭС.

Известно, что показатель световозвращения (ПСВ) оптико-электронных приборов R(p) связан с их ЭПР σ(р) следующей зависимостью [В.Р.Муратов, Ю.А.Филимонов, А.Ф.Ширанков О терминологии, связанной со световозвращающим отражением, Оптико-механическая промышленность, 1980, №3]:

.

Из выражения (22) следует, что устройство для измерения показателя световозвращения оптико-электронных приборов по патенту 2202814 по классу G02В 23/12 одновременно позволяет измерять и ЭПР ОЭП.

Следует отметить, что входящая в устройство-прототип матрица ПЗС, как это следует из формулы изобретения, предназначена для регистрации индикатрисы отражения ОЭП. При этом индикатриса отражения регистрируется только для условий локации в дальней зоне, соответствующей бесконечному удалению плоскости анализа от лоцируемого ОЭП.

Недостатком устройства-прототипа является наличие систематических погрешностей измерения ЭПР и индикатрис отражения ОЭП, обусловленных:

- невозможностью учета зависимости текущего значения эталонных отражателей ЭПР от дальности их локации;

- невозможностью воспроизведения пространственных характеристик зондирующего излучения в плоскости входного зрачка лоцируемого ОЭП, соответствующих заданной дальности локации формирующей оптической системой устройства;

- невозможностью контроля пространственных характеристик зондирующего излучения в плоскости входного зрачка лоцируемого ОЭП, соответствующих заданной дальности локации;

- измерением значений ЭПР на неопределенной дальности от ОЭП до приемника, а индикатрисы отражения только в дальней зоне локации, соответствующей бесконечному удалению плоскости анализа от лоцируемого ОЭП;

- невозможностью определения знака кривизны волнового фронта индикатрисы отражения ОЭП;

- не контролируемым режимом работы систем автоматической регулировки усиления (АРУ) в электронном тракте матрицы ПЗС.

Указанные причины возникновения систематических погрешностей обусловлены принципами построения, способами технической реализации и установки основных элементов в оптическом тракте устройства-прототипа.

С целью подтверждения наличия приведенных выше причин возникновения систематических погрешностей предварительно проведем подробный анализ физических процессов, происходящих при облучении ОЭП лазерными пучками и переотражении ОЭП этих пучков в обратном направлении.

Физика процесса облучения ОЭП лазерным пучком заключается в следующем.

Известно, что при облучении ОЭП пучками с разными значениями знака и радиуса кривизны перетяжка сфокусированного объективом пучка будет смещаться относительно параксиального фокуса объектива. При этом:

абсолютная величина смещения перетяжки относительно параксиального фокуса объектива будет обратно пропорциональна радиусу кривизны волнового фронта;

при облучении ОЭП расходящимся пучком перетяжка относительно параксиального фокуса будет смещаться в сторону удаления от объектива;

при облучении ОЭП сходящимся пучком перетяжка относительно параксиального фокуса будет смещаться в сторону приближения к объективу;

при увеличении смещения точки пересечения прошедших через объектив его лучей с оптической с его осью относительно отражающей поверхностью оптического элемента, расположенного в фокальной плоскости объектива, значение ЭПР ОЭП будет уменьшаться.

Из изложенного выше следует, что помимо аберрационных характеристик объектива ОЭП форма индикатрисы отражения ОЭП и ее максимальное значение будет зависеть от значения знака и радиуса кривизны пучка излучения в плоскости входного зрачка лоцируемого ОЭП.

В тоже время известно, что в ходе процесса локации ОЭП, как правило, используются расходящиеся лазерные пучки [А.В.Павлов. Характеристики излучения и методы из расчета. М.: МО СССР, 1979, 148 с.].

При этом необходимо учитывать положение, согласно которому реальный лазерный пучок представляет собой волну, отличную как от сферической, так и от плоской волны. Так, основным отличием лазерного пучка от сферических и плоских пучков является то, что на заданном уровне энергии он ограничен однополосным гиперболоидом вращения, ось которого совпадает с осью резонатора [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.].

В общем случае огибающую лазерного пучка в плоскости, проходящей через его центр, можно описать с помощью следующего выражения [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.]:

где:

а - радиус пучка в перетяжке (минимальном сечении) пучка;

b - конфокальный параметр резонатора, равный значению Х, при котором значение асимптоты гиперболы равно а;

Х - расстояние от плоскости анализа до перетяжки.

Физический смысл параметров а и b наглядно виден на Фиг.5.

В [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.] также показано, что условия преобразования линзой лазерного пучка отличаются от условий преобразования сферического пучка, поскольку:

- плоскости перетяжек исходного и сформированного линзой пучков не являются взаимно сопряженными, то есть сформированная перетяжка не является изображением исходной;

- параметры гиперболы а и b, описывающей преобразованный линзой пучок, а также положение его перетяжки зависят от параметров исходной гиперболы, дальности от перетяжки исходного пучка до линзы и от фокусного расстояния линзы.

В дополнение к изложенному выше необходимо отметить следующий факт. Поскольку огибающая пучок гипербола сформирована множеством распространяющихся в нем отдельных лучей, то можно найти параметры отдельного крайнего луча, являющимся касательным к гиперболе в точке его соприкосновения с поверхностью линзы. В связи с тем, что толщина линзы мала по сравнению с радиусами кривизны ее поверхностей, линзу можно считать тонкой. Тогда уравнение касательной (искомого луча) примет следующий вид [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.]:

где: а и b - параметры гиперболы;

Х - текущее значение координаты на оси пучка;

Х_П - удаление линзы от перетяжки.

Из выражения (24) нетрудно получить формулу для оценки значения координаты точки пересечения касательной с осью Х относительно плоскости перетяжки:

Смысл значения ΔХ ясно виден на Фиг.6.

Из выражения (25) следует, что точка пересечения крайних касательных в пучке с осью Х зависит только от параметра b гиперболы и дальности от линзы до перетяжки. Это, в свою очередь, свидетельствует о том, что на линзу, удаленную на расстояние Х_П от перетяжки, падает сферический фронт, радиус которого R определяется следующим выражением

С учетом (26) и простых геометрических соображений можно получить выражение, позволяющее проводить точную оценку угловой расходимости лазерного пучка, падающего на линзу (объектив ОЭП), удаленную на расстояние Х_П от перетяжки пучка зондирующего излучения

или

В тоже время в [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.] было показано, что основным требованием к пространственному подобию условий облучения входного зрачка лоцируемого ОЭП на реальных и моделируемых трассах является равенство углов прихода падающих на зрачок лучей в обоих этих случаях.

Поскольку выражения (27а) и (27б) справедливы для углов прихода в обоих случаях, то условие подобия может быть обеспечено только при выполнении следующего равенства:

где: R_ОЭП - радиус входного зрачка ОЭП;

Х_{П р} и Х_{П м} - дальность от входного зрачка ОЭП до перетяжки в реальных и моделируемых условиях соответственно;

ΔХ_р и ΔХ_м - дальность от точки пересечения касательных до плоскости перетяжки в реальных и моделируемых условиях.

Для последующего анализа с учетом (25) приведем выражение (28) к следующему виду

Анализ выражений (28) и (29) показывает следующее:

- для оценки и соблюдения условия подобия облучения входного зрачка в моделируемых условиях реальным условиям необходима исходная информация о параметрах гипербол, огибающих реальный и моделируемый пучки, а также значения расстояний между перетяжками этих пучков и входными зрачками реального и моделируемого ОЭП;

- в общем случае условия подобия могут быть обеспечены с помощью только одного коллиматора, реализующего заданные параметры гиперболы и расстояние до перетяжки.

Необходимо отметить, что практически во все вышеприведенные выражения в качестве исходных данных входят параметры гиперболы, огибающей исходный лазерный пучок. Однако, как правило, в паспортных данных на лазер они отсутствуют.

В тоже время они достаточно просто могут быть найдены экспериментально. Поскольку лазерные пучки имеют относительно небольшую расходимость (порядки десятка угловых минут) в качестве значения размера перетяжки можно принять радиус пятна на выходе лазера, который, как правило, приводится в паспорте на лазер. Данное приближение становится полностью справедливым для газовых лазеров, у которых перетяжка совпадает с выходным зеркалом. Для других типов лазеров принято считать, что перетяжка находится на середине резонатора. Параметр b_ИЗИ пучка может быть вычислен с помощью выражения, полученного из (23):

где:

a_u - радиус перетяжки пучка ИЗИ;

у(L) - радиус пятна на экране, удаленном на расстояние L от лазера.

Практика показывает, что для расчета b_ИЗИ реальных лазеров длина измерительной трассы может не превышать 10÷15 м. Необходимо отметить, что практически во все вышеприведенные выражения в качестве исходных данных входят параметры гиперболы, огибающей исходный лазерный пучок. Однако, как правило, в паспортных данных на лазер они отсутствуют.

В тоже время они достаточно просто могут быть найдены экспериментально. Поскольку лазерные пучки имеют относительно небольшую расходимость (порядки десятка угловых минут) в качестве значения размера перетяжки можно принять радиус пятна на выходе лазера, который, как правило, приводится в паспорте на лазер. Данное приближение становится полностью справедливым для газовых лазеров, у которых перетяжка совпадает с выходным зеркалом. Для других типов лазеров принято считать, что перетяжка находится на середине резонатора. Параметр b_ИЗИ пучка может быть вычислен с помощью выражения, полученного из (23):

где:

a_u - радиус перетяжки пучка ИЗИ;

у(L) - радиус пятна на экране, удаленном на расстояние L от лазера.

Практика показывает, что для расчета b_ИЗИ реальных лазеров длина измерительной трассы может не превышать 10÷15 м.

В тоже время из законов геометрической оптики следует, что при удалении ОЭП от источника лазерного излучения угловая расходимость пучка, прошедшего через входной зрачок ОЭП, будет уменьшаться, что в свою очередь, приведет к уменьшению расстояния между параксиальным фокусом объектива ОЭП и плоскостью перетяжки с фокусированного им пучка.

В качестве примера была проведена численная оценка зависимости углов прихода касательных к огибающей пучок гиперболе в плоскости входного зрачка ОЭП от дальности. При расчетах использовались следующие исходные данные:

- радиус перетяжки лазерного пучка а равен 2 мм;

- параметр гиперболы пучка b, определяющий его угловую расходимость, равен 2000 мм;

- расстояние между входной линзой коллиматора и перетяжкой равно 100 мм;

- фокусные расстояния входной и выходной линзы коллиматора соответственно равны 20 и 200 мм, коэффициент увеличения коллиматора равен 10;

- расходимость пучка на выходе коллиматора равна одной угловой минуте.

С помощью выражений, приведенных в [И.И.Пахомов, А.Б.Цибуля. Расчет оптических систем лазерных приборов. М.: Радио и связь, 1986, 151 с.] для перечисленных выше исходных данных были рассчитаны параметры пучка на выходе коллиматора и в плоскости входного зрачка ОЭП для различных расстояний между зрачком и локатором. Расчеты показали, что выходящий из коллиматора локатора пучок характеризуется следующими параметрами:

- диаметр пучка на выходе коллиматора равен 19.95 мм;

- угловая расходимость, составляющая одну минуту, достигается при расстоянии 0.55 мм от входной линзы коллиматора к выходной;

- параметр b (см. Фиг.6) равен 5.276·10³ мм;

- расстояние между перетяжкой и выходной линзой равно 7.234·10⁴ мм (пучок расходящийся).

На Фиг.7 приведена графическая зависимость этих углов от дальности локации. На Фиг.7 по оси Х отложены значения угловой расходимости лазерного пучка, проходящего через входной зрачок ОЭП, выраженные в радианах, а по оси Х - расстояние между ОЭП и перетяжкой лазерного пучка, выраженное в сантиметрах. Из приведенной на Фиг.7 зависимости видно, что значения углов прихода касательных к гиперболам пучков во входном зрачке ОЭП диаметром 50 мм на дальностях 3 км и 30 м соответственно равны 8.132·10^-6 и 2.443·10^-4 рад. Эти значения соответствуют 1,8 угловым секундам и 8.4 угловым минутам. То есть при изменении дальности локации с 30 м до 3 км угол прихода изменяется почти в триста раз.

Этот факт показывает, что в ходе измерения характеристик отражения ОЭП (ЭПР и индикатрисы) в лабораторных условиях необходимо воспроизводить условия облучения входного зрачка ОЭП, соответствующие реальным (заданным) дальностям локации.

Физика процесса отражения ОЭП ла