Устройство видения объекта

Устройство видения объекта

Иллюстрации

Показать все

Реферат

Изобретение относится к оптическому приборостроению, к устройствам видения объектов, и может быть использовано при конструировании оптических систем построения изображения различного назначения со средствами защиты оптических и оптико-электронных узлов от воздействия излучения, в частности, лазерного, а также для решения широкого спектра народнохозяйственных задач, связанных с управлением интенсивностью и направлением света. За устройствами, содержащими объектив для формирования изображения и фотоприемник и размещаемыми на аэрокосмических носителях, в последнее время в научно-технической литературе закрепился термин "устройства видения".

К числу таких задач можно отнести дистанционное зондирование земной поверхности фотографическими и оптико-электронными системами, высокоточное измерение текущих навигационных параметров космических аппаратов, мониторинг околоземного космического пространства. При разработке измерительных и регистрирующих систем учитывается возможность ослепления фотоприемных устройств в оптическом диапазоне в силу высокой чувствительности последних. Проблема защиты оптико-электронных систем от воздействия излучения актуальна в особенности при геодезической съемке, регистрации удаленных объектов, практической космонавтике.

Известны устройства видения объекта с защитой оптических систем от воздействия лазерного излучения одноразового действия. Это оптические системы построения изображения с тонким пленочным зеркалом на стеклянной подложке и размещенным между зеркалом и подложкой в капсуле из эпоксидной смолы зарядом взрывчатого вещества, детонирующим при облучении лазерным излучением. Или устройства видения с затворами невзрывного типа с использованием прогорающих зеркал при облучении системы излучением с интенсивностью выше определенного порога.

Однако такие устройства обладают низким ресурсом работы, требуют постоянной замены, сложны в изготовлении, и их эксплуатация связана с использованием средств защиты оптики от продуктов взрыва и горения.

Известны устройства видения объекта с использованием специальных затворов многоразового действия, предотвращающих ослепление регистрирующих систем.

Это "Устройство для наблюдения удаленных объектов с узлом защиты от воздействия лазерного излучения" [Пат. RU №2089887, МПК G01N 21/84, приор, от 24.03.95.]. Устройство включает объектив, фотоприемник с фотозатвором, выполненным в виде коромысла на подвесе. На одном плече коромысла укреплено поворотное зеркало, направляющее в объектив световой поток, а на другом плече противовес. При попадании на поворотное зеркало помеховой (лазерной) засветки коромысло под действием светового давления поворачивается и смещает световой поток с входного зрачка объектива, защищая фотоприемник от ослепления.

Однако время срабатывания затвора велико для надежной защиты фотоприемника.

Известно устройство видения объекта с системой защиты фотоприемника от ослепления, выбранное нами в качестве прототипа [С.В.Кулагин, А.С.Гоменюк, В.Н.Дикарев и др. «Оптико-механические приборы», М.: «Машиностроение», 1984, с.161-162]. Устройство включает объектив, формирующий изображение объекта на фотоприемнике, затвор, состоящий из световой заслонки и привода, обеспечивающего ее перемещение, и электронного узла, вырабатывающего сигнал на закрывание заслонки.

Устройство функционирует следующим образом. Объектив формирует на фотоприемнике (например, ПЗС-матрице) изображение объекта. Часть светового пучка, поступающего во входной зрачок объектива от объекта регистрации, попадает на электронный узел, размещенный в ходе лучей за объективом. Узел вырабатывает сигнал, пропорциональный попавшей на него энергии. Сигнал поступает далее на привод световой заслонки. Чем выше яркость объекта, тем больше вырабатываемый сигнал, тем больше заслонка перекрывает световой поток, поступающий на фотоприемник, защищая его от ослепления.

Однако скорость срабатывания затвора и в этом техническом решении невелика (около 10 м/с). Поэтому для смещения заслонки на величину, равную размеру светочувствительной площадки фотоприемника (около 1-2 см), требуется время 1-2 мс. Это время недостаточно мало для надежной защиты приемника от импульсного лазерного излучения: случайного блика или световой помехи. Степень распознавания удаленных объектов у таких систем невелика.

Предложенное нами изобретение при минимальных массо-габаритных характеристиках системы построения изображения обеспечивает видение объекта с высокой степенью распознавания и с высокой степенью защиты оптической системы от ослепления. Оно удобно и надежно в работе, дает стабильные результаты.

Нами теоретически обосновано и экспериментально подтверждено, что возможно построение полного, не искаженного изображения предмета, представленного выборочными значениями непрерывной функции, т.е. интенсивностью в отдельных точках, не только при выполнении условий теоремы Котельникова (двумерный вариант теоремы приведена [1]).

Несколько неискаженных изображений предмета мы получили при размещении дифракционной решетки в сходящемся пучке лучей и выполнении щелей решетки специально выбранной формы, а именно, вырезанными вдоль ветвей семейства гипербол, описываемых уравнением определенного вида, и выполнении при этом специально выбранных условий.

Заявленный технический результат получен нами, когда в устройстве видения объекта, включающем установленные на оптической оси объектив для формирования изображения объекта, размещенный в сходящемся пучке лучей фотозатвор с приводом, соединенным с электронным узлом, вырабатывающим сигнал для срабатывания затвора, и фотоприемный узел с блоком обработки информации, новым является то, что фотозатвор выполнен в виде установленных с возможностью движения вдоль линии дисперсии навстречу друг другу и нормально к оптической оси двух параллельных пластин, в каждой из которых выполнены образующие дифракционные решетки щели, вырезанные вдоль ветвей семейства гипербол, описываемых уравнением:

причем a² и b² - выбраны из условия:

где а - действительная полуось гипербол, лежащая на оси дисперсии решетки;

b - мнимая полуось;

х и y - декартовы координаты в плоскости пластин,

n - номер гиперболы в семействе, который последовательно принимает значения ряда целых чисел 0, 1, 2 и т.д.;

λ_m - минимальная длина волны излучения, формирующего изображение;

d - размер фотоприемника вдоль оси, лежащей в плоскости фотоприемника и параллельной оси дисперсии;

l - расстояние от фотоприемника до пластины, которое выбрано из условия выполнения скалярной теории дифракции;

щели выполнены одинаковой ширины t, которая выбрана из условия t≤Т/2,

где Т - минимальное в семействе расстояние между ветвями соседних гипербол,

при этом блок фотоприемников и блок обработки сигнала выполнены многоспектральными.

Гипербола, задаваемая уравнением вида:

состоит из двух ветвей (см. фиг.2), симметрично расположенных относительно оси y: левой ветви 14 и правой ветви 14' гиперболы. Расстояние PQ между вершинами ветвей называют действительной осью гиперболы и обозначают как 2а. Расстояние MN между точками, лежащими на асимптотах 15 и 16, называют мнимой осью гиперболы и обозначают как 2b. Как следует из (1), каждая гипербола однозначно определяется величиной своих осей а и b, причем, если a²=(nλb)²/(d²-(nλ))² и b²=(d/2)²+l²-(nλ/2)², то, считая d, l и λ заданными числами и придавая n ряд последовательных целочисленных значений n=0; 1; 2; 3 и т.д., получим набор значений а и b, и соответственно этому набору по уравнению (1) семейство гипербол на плоскости с координатами (х, y). Значению n=0 соответствует вырожденная гипербола 12, которая совпадает с осью y. Значению n=1 соответствует ближайшая к ней гипербола, ветви 14 и 14' которой симметрично расположены относительно оси y. Щели, вырезанные вдоль ветвей гипербол, образуют дифракционную решетку: световые пучки, падающие на решетку, отклоняются вдоль оси x, и по отношению к решетке эта ось будет осью дисперсии. То есть, ось дисперсии совпадает с действительной осью гиперболы.

Скалярная теория дифракции применяется для решения задач инструментальной оптики. Расчеты, выполненные в соответствии со скалярной теорией, согласуются с экспериментом при условии, что длина волны мала по сравнению с размером препятствия, на котором происходит дифракция [2, с.416]. Системы, формирующие изображение и содержащие амплитудные решетки, корректно рассчитываются в рамках скалярной теории, если размер щелей значительно превосходит длину волны излучения [2, с.440]. На практике соответствие реальных параметров устройств расчетным значениям реализуется, если размер щели пятикратно или более превосходит длину волны.

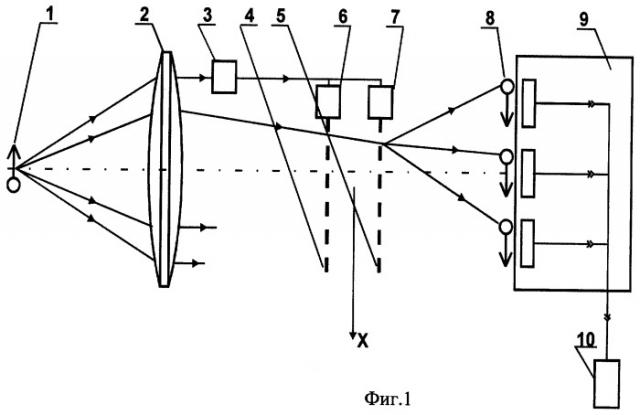
На фиг.1 представлена схема устройства видения объекта с фотозатвором, где объект 1, объектив 2, электронный узел 3, вырабатывающий сигнал на закрывание затвора, первая и вторая пластины 4 и 5 с дифракционными решетками, приводы 6 и 7 для смещения решеток, плоскость 8 изображения объекта, фотоприемный узел 9, блок обработки сигналов 10,

х - ось дисперсии дифракционных решеток,

→ - световые лучи,

-» - электрический сигнал, поступающий от фотоприемного узла в блок 10 обработки сигналов,

-•-•- - оптическая ось системы.

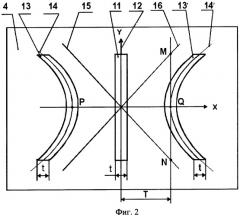
На фиг.2 представлен макет геометрической схемы формирования щелей дифракционных решеток, вырезанных в пластинах вдоль ветвей семейства гипербол, где: пластина 4, щель 11 вдоль вырожденной гиперболы 12 с номером n=0, щели 13 и 13' вдоль ветвей 14 и 14' гиперболы с номером n=1, первая и вторая асимптоты 15 и 16 гиперболы с ветвями 14 и 14',

x - координатная ось, совпадающая с осью дисперсии дифракционных решеток;

y - координатная ось, с которой совпадает вырожденная гипербола;

T - расстояние между гиперболой с номером n=0 и правой ветвью 14' гиперболы с n=1, измеренное вдоль оси дисперсии;

t - ширина щелей дифракционной решетки, измеренная вдоль линии параллельной оси дисперсии;

MN - действительная ось гиперболы, равная 26;

PQ - мнимая ось гиперболы, равная 2а.

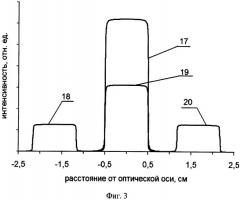
На фиг.3 представлено распределение интенсивности по сечению в плоскости изображения равномерно освещенного образца - квадратного отверстия, где: интенсивность 17 - в изображении, сформированном системой в отсутствие решеток, интенсивность 18 и 20 - в минус первом и плюс первом порядках дифракции, соответственно, интенсивность 19 - в изображении в нулевом порядке дифракции.

Предложенное устройство работает следующим образом. Изображение объекта 1 формируют объективом 2 в плоскости изображения 8, в непосредственной близости от которой расположены фотоприемники 9.

Качество изображения характеризуют разрешающей способностью оптической системы. Предельно возможную (дифракционно ограниченную) разрешающую способность обеспечивает сферическая сходящаяся волна [2, с.235].

Между объективом 2 и плоскостью 8 в сходящемся пучке лучей установлены две одинаковые пластины 4 и 5, в каждой из которых сделаны щелевые отверстия в форме гипербол, подчиняющихся уравнениям (1-3).

В исходном состоянии решетки установлены напротив друг друга, нормально к оптической оси объектива, и их прозрачные участки (щели) совмещены, поэтому часть светового потока от объекта проходит за решетки. При этом за счет дифракции на решетках пучок расщепляется вдоль оси дисперсии x на несколько пучков, каждый из которых формирует в плоскости 8 изображение объекта.

Для того чтобы решетка не вносила искажения в изображение предмета, необходимо, чтобы изображения в плоскости 8, сформированные пучками в отдельных порядках дифракции, не накладывались друг на друга и чтобы волны, распространяющиеся от решеток к плоскости изображения, были сходящимися сферическими волнами.

О неналожении изображений в порядках дифракции.

Размер d фотоприемника в системе видения задается как конструктивный параметр, и, например, для фоточувствительной ПЗС-матрицы этот размер не превышает 1-1,5 см. Будем считать, что система рассчитана согласованной, это значит, что размер регистрируемого изображения также равен d.

Решетка, образованная семейством гипербол, имеет переменный (возрастающий вдоль оси дисперсии) период (расстояние между любыми двумя соседними ветвями гипербол). (Фиг.2 изображает не в масштабе макет решетки: реальная решетка в виде квадрата со стороной 3-5 см содержит порядка 80-100 гипербол (т.е. n - это ряд чисел от 0 до 80-100), а ширина каждой щели около 10 мкм). При этом угол дифракции в первый порядок определяется минимальным периодом решетки. Минимальный период находится на оси дисперсии между гиперболой с n=0 и ветвью гиперболы с n=1. Это расстояние (по определению, см. фиг.2) равно величине полуоси а для гиперболы с n=1. Подставляя в (2) значение b из (3) и полагая n=1, получим;

а²=(λ((d/2)²+l²-(λ/2)²))²/(d²-λ²)

Учитывая, что (d/2)²<<l² (для примера: (d/2)²≅0,25 см², а l²≥100 см²), (λ/2)²<<l², λ²<<d², получим; a=(λl)/d. Минимальное значение а получим при минимальном значении λ=λ_m, а следовательно, и искомый период Т решетки определится выражением Т=(λ_m)/d. Смещение s изображения на расстоянии l составит s=(λl)/T и, подставляя Т, получим, s=(λd)/(λ_m), то есть для любой длины волны излучения λ≥λ_m выполняется условие: s≥d.

Следовательно, определяя параметры решетки по уравнениям (1-3) для минимальной длины волны, обеспечиваем условие неналожения изображений в порядках дифракции.

Таким образом, получаем, что поскольку изображение в первом (а также и минус первом) порядках дифракции смещено с оптической оси вдоль оси дисперсии на величину, не меньшую размера d самого изображения, то изображения в порядках не накладываются друг на друга.

О сферичности сходящихся волн.

С плоскостью решеток связана система координат (х, y). С плоскостью изображения свяжем систему координат (х₁, y₁), оси которой параллельны осям первой системы координат. Приемник размером d займет вдоль оси х₁ отрезок с координатами (-d/2,+d/2). Введем расстояние r₁(x, y) и r₂(x, y), соответственно, от точек (-d/2, 0) и (+d/2, 0) до плоскости (x, y). Тогда для любого числа С уравнение

описывает в плоскости (x, y) гиперболу [3]. Если положим С=nλ, где n - непрерывный ряд последовательных целых чисел, то в плоскости (x, y) получим семейство гипербол, в котором каждому n соответствует своя гипербола (пара ветвей). При этом уравнение (4), выраженное через координаты точек на плоскости (x, y), после преобразований принимает вид, задаваемый соотношениями (1-3).

Амплитудная гиперболическая решетка D(x, y), соответствующая этому семейству, описывается выражением:

где j - мнимая 1;

m - номер члена ряда.

В выражении (5) k=2π/λ - волновое число. Информация о том, что штрихи решетки имеют форму гипербол, заложена в выражении r₁-r₂ под экспонентой.

Пусть на решетку падает сферическая волна U(x, y), сходящаяся в плоскости изображения (x₁, y₁) на оптической оси, т.е. в точке с координатами х₁=0 и y₁=0. Если r₀ - расстояние от точек плоскости (x, y) до точки схождения, то волна U запишется в виде:

где А - амплитуда волны. Такая волна формирует с предельным разрешением изображение предмета в отсутствии решеток.

Если на пути волны установлена решетка D(x, y), то непосредственно за решеткой распределение V(x, y) поля будет равно произведению

которое представляет собой множество сходящихся в плоскости изображения волн, дифрагировавших на решетке. Каждая волна соответствует произведению U на один из членов суммы (5).

Волна, дифрагировавшая в нулевой порядок, связана со свободным членом ряда (5) и дается выражением

Это сферическая сходящаяся волна, тождественная сходящейся волне (6) в отсутствии решеток. Отличие в величине амплитуды (множитель t/T) не влияет на качество изображения. Следовательно, в нулевом порядке дифракции формируется изображение, тождественное изображению в отсутствии решеток.

Волна, дифрагировавшая в плюс первый порядок, описывается произведением U на член ряда (5) с m=+1 и дается выражением:

Покажем, что эта волна - сферическая сходящаяся. Для этого достаточно показать, что величина r₂-r₁+r₀ равна расстоянию r₃, от некоторой точки (точки схождения) до точки с координатами (x, y) в плоскости решеток, то есть выполняется соотношение:

Запишем расстояния в явном виде: , , . Положим d=1 см, l=10 см, х=0,5 см, y=0,5 см. Подставляя эти значения в левую часть (10), получим: r₂-r₁+r₀=10,16157 см.

Положим, что точка схождения имеет координаты х₁=d, y₁=0 и расположена на расстоянии l₁ от плоскости решеток. Расстояние r₃ в явном виде запишется как . Подставляя принятые значения d=1 см, х=0,5 см, y=0,5 см и полагая l₁=9,95025 см, получим r₃=10,16157 см. Равенство r₂-r₁+r₀=r₃ доказывает, что (9) есть сферическая волна, сходящаяся в точке x₁=d, y₁=0 на расстоянии l₁=9,95025 см от решеток. То, что волна сходится на расстоянии l₁=9,95025 см, то есть ближе к решеткам, чем плоскость изображения (l=10 см), вызвано известным явлением в оптике - кривизной поля: плоскость изображения, строго говоря, - (слегка) искривленная поверхность. Это, однако, не снижает качества изображения, так как, во-первых, существуют методы коррекции кривизны, во-вторых, можно скомпенсировать изменение расстояния, передвинув приемник в первом порядке дифракции ближе к решеткам на 0,5 мм, в-третьих, в большинстве оптических систем, используемых на космических носителях, глубина резкости (длина каустики объектива) заметно превышает 0,5 мм. Следовательно, волна, дифрагировавшая в плюс первый порядок, имеет вид:

сферической волны, сходящейся в плоскости изображения к точке, смещенной вдоль оси дисперсии на расстояние d от волны V₀(x, y) в нулевом порядке. Выражение V₁(x, y) свидетельствует о том, что волна в плюс первом порядке дифракции тождественна (с точностью до численного множителя, не влияющего на разрешающую способность системы) волне в отсутствии решеток. Следовательно, в плюс первом порядке дифракции изображение тождественно изображению в отсутствии решеток.

Аналогичный результат можно получить и для волны, распространяющейся в минус первый порядок.

При других формах штрихов решетки волна, дифрагировавшая в плюс первый и минус первый порядок, имеет дополнительное слагаемое к r₃ и, следовательно, содержит аберрации, поэтому изображения в плюс и минус первом порядке дифракции не тождественны изображению в отсутствии решеток.

Таким образом, выбор формы штрихов решеток в виде, соответствующем уравнениям (1-3), позволяет получить, по крайней мере, три изображения, тождественных изображению, полученному в системе без решеток.

Выбор расстояния l от фотоприемника до пластины из условия выполнения скалярной теории дифракции позволяет следующим образом рассчитать его численное значение. Из выражения для ширины щелей t≤T/2 следует, что T≥2t при этом, как показано выше, Т=(λ_ml)/d, и, следовательно,

Как упоминалось, ширина щели в соответствии со скалярной теорией дифракции должна быть значительно больше λ, на практике достаточно положить t≥5λ_max, где λ_max - максимальная длина волны излучения, формирующего изображения. Подставляя это значение в (11), получим выражение для численного расчета величины l≥10d(λ_max/λ_m).

Фотоприемный узел 9 состоит из нескольких отдельных фоточувствительных элементов, каждый из которых (фиг.1) имеет свою область спектральной чувствительности. Поэтому сигнал, поступающий из узла в блок 10 обработки, содержит изображение одного и того же объекта в нескольких спектральных диапазонах. Выделение конкретной спектральной области, в которой на данном фотоприемнике регистрируют изображение, может быть выполнено, например, подбором материала фотоприемника, либо путем помещения перед каждым фотоприемником отдельного светофильтра, выделяющего соответствующий спектральный диапазон. Подходы к решению этой задачи известны.

На фиг.3 представлено распределение интенсивности по сечению в плоскости изображения равномерно освещенного квадратного отверстия. Распределения получены расчетом с использованием формул (6), (8) и (9). При установке решеток интенсивности в изображениях (18, 19, 20) ниже, чем в изображении без решеток (17). Однако разрешающая способность одинакова во всех четырех изображениях. Это доказывается тем, что если изображения путем изменения масштаба привести к одной высоте и наложить друг на друга, то они совмещаются всеми своими точками.

Размещение в сходящемся пучке двух пластин с решетками в виде семейства гипербол позволяет получить как минимум три раздельных изображения, тождественных объекту и зарегистрированных в трех различных спектральных диапазонах.

Совместная обработка изображений одного и того же объекта, полученных в различных спектральных диапазонах, позволяет существенно расширить возможности космических систем наблюдения (видения), получить качественно новую информацию о земной поверхности [4-6], что особенно актуально при многоспектральном дистанционном зондировании земной поверхности, относящемся к числу наиболее важных направлений развития прикладной космической оптики.

С другой стороны, выбор ширины щели t из условия t≤T/2, где Т - минимальное расстояние между соседними гиперболами, позволяет выполнить быстрое закрывание затвора, поскольку в этом случае ширина прозрачной части t решеток не превышает ширины непрозрачной части.

В момент облучения объектива помеховой лазерной засветкой часть светового потока поступает на электронный узел 3, вырабатывающий сигнал на закрывание затвора. Сигнал от электронного узла поступает на оба привода 6 и 7 решеток. Каждая из решеток смещается навстречу друг другу на половину ширины щели и перекрывает опасный световой поток, поскольку ширина каждой щели не превышает размера непрозрачного промежутка. Для закрывания достаточно сместить каждую решетку на расстояние, равное половине ширины щели (около 5 мкм). При оптимальном выборе привода 6 и 7 такое смещение может быть выполнено за время до 10 мкс. Это время достаточно мало, чтобы успеть закрыть затвор и обеспечить защиту фотоприемника от лазерной помехи.

Ширину щелей в решетках выбирают следующим образом (фиг.2).

Минимальный промежуток Т между двумя соседними кривыми (ветвями гипербол) находится между гиперболой 12 с n=0, совпадающей с осью y, и соседней с ней ветвью 14 гиперболы с n=1 (то же самое можно сказать про ветвь 14', так как ветви симметричны относительно оси y). Этот промежуток расположен на оси x дисперсии. Вдоль каждой ветви вырежем отверстие в виде щели (11, 13, 13' на фиг.2), считая центральной линией щели соответствующую ветвь гиперболы, а ширину щели t, измеренную вдоль оси дисперсии, установим равной T/2. В этом случае прозрачные части решетки не шире непрозрачных частей. Поэтому, если изготовить две одинаковые решетки, прорезав в металлических пластинах щели, как указано выше, и совместить решетки, то при их взаимном смещении вдоль оси дисперсии навстречу друг другу на расстояние t прозрачные части одной решетки полностью закроются непрозрачными частями другой решетки.

Следовательно, такая пара решеток может служить затвором для светового потока, проходящего через решетки. Полное закрывание затвора произойдет также в том случае, если ширина t прозрачных щелей будет меньше T/2. Поэтому ширина щелей t может быть выбрана из условия t≤T/2, где Т - минимальное расстояние между соседними гиперболами, которое среди всего семейства гипербол получается для гипербол с номерами n=0 и n=1 на оси дисперсии.

Таким образом, предложено устройство видения, позволяющее с высокой степенью распознавания получать изображения удаленных объектов. Высокая степень распознавания обеспечивается путем регистрации неискаженных изображений в нескольких спектральных диапазонах. Такой метод позволяет с предельным разрешением и контрастом зарегистрировать в каждом отдельном спектральном диапазоне свой набор элементов предмета (например, в инфракрасном диапазоне с предельным разрешением и контрастом регистрируются нагретые части объекта, в ультрафиолетовом - металлические и т.д.). Результирующее изображение получается как синтез высококачественных изображений в отдельных диапазонах. Этим обеспечивается высокая степень распознавания удаленных объектов.

Малая ширина щелей решетки (около 10-15 мкм) позволила реализовать быстродействующий затвор, который защищает оптическую систему от повреждения помеховой засветкой.

Литература

1. Дж.Гудмен. Введение в фурье-оптику. М., Мир, 1970, с.39-44.

2. М.Борн, Э.Вольф. Основы оптики. М.: Наука, 1970.

3. И.Н.Бронштейн и К.А.Семендяев. Справочник по математике. М., ГИТТЛ, 1954, с.206.

4. А.В.Перцов. Состояние и направление развития методологии космоаэрогеологических исследований. Исследование Земли из космоса, 1995, №2, с.46-49.

5. Б.В.Шилин, В.В.Хотяков. Видеоспектральная аэросъемка - ведущее направление развития дистанционного зондирования в оптическом диапазоне. Оптический журнал, 2004, том 71, №3, с.55-58.

6. В.Ф.Фатеев, Г.Н.Мальцев. Прикладная оптика и космос. Оптический журнал, 2000, том 67, №7, с.3-4.

Устройство видения объекта, включающее установленные на оптической оси объектив для формирования изображения объекта, размещенный в сходящемся пучке излучения фотозатвор с приводом, соединенным с электронным узлом, вырабатывающим сигнал для срабатывания затвора, и фотоприемный узел с блоком обработки информации, отличающийся тем, что фотозатвор выполнен в виде установленных с возможностью движения вдоль линии дисперсии навстречу друг другу и нормально к оптической оси двух параллельных пластин, в каждой из которых выполнены образующие дифракционные решетки щели, вырезанные вдоль ветвей семейства гипербол, описываемых уравнением:

причем а² и b² - выбраны из условия:

где a - действительная полуось гипербол, лежащая на оси дисперсии решетки;

b - мнимая полуось;

х и y декартовы координаты в плоскости пластин;

n - номер гиперболы в семействе, который последовательно принимает значения ряда целых чисел 0, 1, 2 и т.д.;

λ_m - минимальная длина волны излучения, формирующего изображение;

d - размер фотоприемника вдоль оси, лежащей в плоскости фотоприемника и параллельной оси дисперсии;

l - расстояние от фотоприемника до пластины, которое выбрано из условия выполнения скалярной теории дифракции;

щели выполнены одинаковой ширины t, которая выбрана из условия t≤T/2, где Т минимальное в семействе расстояние между ветвями соседних гипербол,

при этом блок фотоприемников и блок обработки сигнала выполнены многоспектральными.