Способ прогнозирования развития гипоплазии кроветворения при цитостатической терапии больных иммуноопосредованными заболеваниями нервной и мышечной систем
Иллюстрации
Показать всеИзобретение относится к медицине, а именно к неврологии, и может быть использовано для прогнозирования развития гипоплазии кроветворения при цитостатической терапии больных иммуноопосредованными заболеваниями нервной и мышечной систем. Сущность способа: у больного определяют количество форменных элементов крови до начала лечения и повторно в процессе лечения. Затем на основании полученных данных определяют коэффициент пропорциональности k, зависящий от индивидуальных свойств организма больного, по формуле Q=Q0ekt, где Q - количество форменного элемента крови, Q0 - количество форменного элемента крови до начала лечения, t - длительность цитостатической терапии, в днях, принимая, что Q=Q1, где Q1 - количество форменных элементов крови при повторном анализе, t=t1, где t1 - длительность цитостатической терапии до повторного анализа крови, в днях. Далее, используя полученные значения Q0 и k, по формуле для расчета Q определяют срок прогнозируемого развития гипоплазии кроветворения. Использование способа позволяет повысить точность и эффективность прогнозирования побочных эффектов при цитостатической терапии, а также дает возможность проведения патогенетической терапии с возможностью предупреждения лейкопении. 2 ил.
Реферат
Изобретение относится к медицине, а именно к неврологии, и может быть применено для решения фундаментальных задач гематологии. Применение данного изобретения позволит проводить патогенетическую терапию с возможностью предупреждения лейкопении.
При лечении иммуноопосредованных заболеваний нервной и мышечной систем, таких как: хроническая воспалительная демиелинизирующая полиневропатия, хронический аутоиммунный полимиозит, миастения Gravis, прогредиентные формы рассеянного склероза, поражения нервной системы при диффузных заболеваниях соединительной ткани и системных васкулитах, а также при лечении ряда онкологических заболеваний, применяются цитостатические препараты, например азатиоприн. Известны побочные эффекты данной группы препаратов, одним из которых является панцитопения, вследствие чего снижается резистентность организма к инфекциям, возникают нарушения в свертывающей системе крови, гемическая гипоксия тканей. Другой причиной развития панцитопении является воздействие на человека доз проникающих радиоактивных излучений, превышающих допустимые нормы. Однако до сих пор не найдены математические модели, адекватно описывающие процесс снижения количества форменных элементов крови, при применении результатов которых возможно решение задачи прогноза уровня лейкоцитов, тромбоцитов, эритроцитов в сыворотке крови. В прикладной медицине нередко возникают ситуации, когда даже опытный врач, назначая цитостатики, не может быть уверен в том, что пациенты в силу своего физического состояния (например, больные с центральным или периферическим парапарезом, тяжелой миастенией) или удаленности лабораторной службы, будут выполнять его рекомендации по контролю форменных элементов крови в процессе лечения. Т.е. несмотря на существующие мировые рекомендации [1] о контроле за содержанием форменных элементов крови в процессе терапии цитостатиками в виде выполнения клинического анализа крови 1 раз в 14 дней, пациенты не всегда придерживаются строгих рекомендаций. Возникает противоречивая ситуация: с одной стороны врачу из опыта работы известно, что адекватного лабораторного контроля не будет, с другой, следуя показаниям, врач обязан назначить цитостатики. Изложенное противоречие может быть решено либо расширением сети учреждений лабораторной службы, что в настоящее время сопряжено со значительными экономическими трудностями, либо созданием способа, применение которого позволяет прогнозировать состояние больного.
Известен способ прогнозирования развития гипоплазии кроветворения при цитостатической терапии больных иммуноопосредовнными заболеваниями нервной и мышечной систем (Иммуносупрессивная химиотерапия: Пер. с нем. / Под ред. Д.Нелиуса. - М.: Медицина, 1984, - 288 с., с.68-69) [1], согласно которому при динамическом наблюдении за пациентами необходимо исследовать клинический анализ крови, осуществлять контроль за функцией печени (контроль билирубина, АЛТ, ACT), осуществлять контроль за функцией почек (креатинин, мочевина, общий анализ мочи), исследование белков сыворотки крови, иммуноглобулинов, циркулирующих аутоантител. Интервалы между необходимыми исследованиями опубликованы в [1, с.69], причем, как указывается в монографии, в зависимости от конкретной ситуации интервалы могут меняться. Недостатком существующего метода, по мнению авторов монографии, является то, что, несмотря на исследование периферической крови, результат влияния цитостатиков на гемопоэз распознается поздно и безобидное уменьшение количества гранулоцитов может внезапно перейти в агранулоцитоз. Т.е. недостатками этого способа является невозможность выполнения прогноза гипоплазии кроветворения для своевременной коррекции терапии.
Технический результат, на достижение которого направлено настоящее изобретение, заключается в повышении эффективности прогнозирования побочных эффектов при цитостатической терапии, путем создания математической модели, адекватно описывающей процесс снижения количества форменных элементов крови при лечении больных иммуноопосредованными заболеваниями нервной и мышечной систем цитостатиками и позволяющую без применения большого количества лабораторных исследований с требуемой в медицине точностью определять срок, при котором следует осуществлять коррекцию терапии.
Методологической основой исследования является поиск дифференциального уравнения, семейства решений которого есть аналитическое описание временного изменения форменных элементов крови.
Указанный технический результат достигается за счет того, что в способе прогнозирования развития гипоплазии кроветворения при цитостатической терапии больных иммуноопосредованными заболеваниями нервной и мышечной систем, включающем клинический анализ крови, согласно изобретению, у больного определяют количество форменных элементов крови до начала лечения и повторно в процессе лечения, на основании полученных данных по формуле Q=Q0ekt, где
Q - количество форменного элемента крови,
Q0 - количество форменного элемента крови до начала лечения,
t - длительность цитостатической терапии в днях,
принимая, что
Q=Q1, где Q1 - количество форменных элементов крови при повторном анализе,
t=t1, где t1 - длительность цитостатической терапии до повторного анализа крови, в днях,
определяют коэффициент пропорциональности k, зависящий от индивидуальных свойств организма больного, и, используя полученные значения Q0 и k, по формуле для расчета Q определяют срок прогнозируемого развития гипоплазии кроветворения.
Следуя существующим рекомендациям по составлению дифференциальных уравнений [2] (Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. - 2-е изд., испр. - М.: Физматлит, 2001, - 320 с.), обозначим через Q количество лейкоцитов в сыворотке крови в начальный момент времени. Используя результаты решений известной задачи о брахистохроне [3] (Классики естествознания. Под общ. ред. И.И.Агола, С.И.Вавилова, М.Я.Выгодского, Б.М.Гессена, М.Л.Левина, А.А.Максимова, А.А.Михайлова, И.П.Роцена и А.Я.Хинчина. Метод нахождения кривых линий, обладающих свойствами максимума, либо минимума или решение изопериметрической задачи, взятой в самом широком смысле Леонарда Эйлера королевского профессора и члена императорской петербургской академии наук. М.-Л.: Государственное технико-теоретическое издательство. 1934, - 600 с., с.12) будем считать, что аналитическое выражение, описывающее закон снижения количества лейкоцитов в сыворотке крови, есть монотонно убывающая дифференцируемая функция, т.е, Q(t)∈C1.
Пусть в момент времени t количество лейкоцитов в крови равно Q. Тогда, применив результаты теоремы Лагранжа [4] (Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. Изд. 7-е стереотипное. М.: Издательство «Наука» Главная редакция физико-математической литературы. 1969. - 607 с., с.226), приходим к заключению, что за бесконечно малый промежуток времени dt количество лейкоцитов dQ, на которое произошло снижение их количества, по предположению, равно
где k - коэффициент пропорциональности, зависящий от индивидуальных свойств организма, q - минимально возможное количество лейкоцитов в крови человека.
Из физиологических соображений очевидно, что q - неотрицательная константа. Неумаляя общности будем считать, что q=0. Нетрудно заметить, что уравнение (1) есть дифференциальное уравнение с разделяющимися переменными. Выполнив разделение переменных, находим, что
Взяв квадратуры, находим общий интеграл
Потенцируя обе части равенства (3) и выполнив очевидные преобразования, находим, что аналитическое выражение
есть общее решение уравнения (1), представленное двухпараметрической интегральной кривой семейства решений.
Начальные условия Q0=Q при t=0 дает возможность найти численное значение постоянной интегрирования С:
Q0=С=const.
Таким образом, находим:
Q=Q0·еkt
Коэффициент k может быть найден применением дополнительных условий Q=Q1
при
t=t1, что в рамках постулата непрерывности времени t позволят использовать аналитическое выражение (4) в качестве математической модели изменения количества лейкоцитов Q в крови пациента.
Применение найденного результата - аппроксимационной кривой, являющейся математической моделью, записанной аналитическим выражением (4), позволяет выполнить прогноз количества лейкоцитов в сыворотке крови человека при диагностике и лечении ряда заболеваний.
В целях полноты изложения, рассмотрим применение модели (4) в рамках конкретного примера.
Пример 1. Больному З., находившемуся на лечении в ГМПБ №2 (№17528 - С) с диагнозом хроническая воспалительная демиелинизирующая полиневропатия была назначена патогенетическая терапия - лечение таблетированной формой азатиоприна в дозировке 2 мг/кг веса два раза в сутки. В клиническом анализе крови от 9.07.02 число лейкоцитов было 9.6·109/л. При исследовании от 23.08.02 число лейкоцитов снизилось до 2.6·109/л. (№23702 - С). В силу своего физического состояния в виде наличия у больного грубого периферического тетрапареза и удаленности лабораторной службы (пациент не являлся жителем Санкт-Петербурга), выполнение клинического анализа крови по предложенной рекомендации 1 раз в 14 дней, не представлялось для него возможным.
Таким образом, концептуально-структурной задачей в нашем случае является нахождение зависимости между дозами приема азатиоприна и ответной реакцией организма, проявляющейся как изменение количества лейкоцитов крови.
Выполним математическую постановку задачи. Применив общее решение (4) дифференциального уравнения (2) и применив результаты клинических анализов крови больного, найти частное решение уравнения (2). А именно, из семейства решений, заданных аналитическим выражением (4), найти аналитическое выражение, описывающее интегральную кривую, учитывающую индивидуальные особенности конкретного больного.
Исходными численными значениями результатов измерений в нашем случае являются:
1) дата первого анализа крови больного, выполненного до назначения азатиоприна - 9.07.02.
2) количество лейкоцитов в крови больного 9.07.02, до приема азатиоприна - 9.6·109/л.
3) дата повторного анализа крови больного, выполненного после прохождения 46 дневного курса лечения азатиоприном - 23.08.02.
4) результаты анализа - содержание лейкоцитов в крови больного 23.08.02 - 2.6·109/л.
Применением результатов измерений, перечисленных в пунктах 1,2, сформулируем задачу Коши [5] (Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Изд. 3-е испр. и доп. М.: Издательство «Высшая школа», 1967, - 564 с., с.21). Будем считать, что 9.07.02 соответствует моменту времени t0=0, начальное значение количества лейкоцитов Q0=9.6·109/л. Сформулируем дополнительное условие. Так как между 9 июля и 23 августа прошло 46 дней, то момент времени t1=46, соответствующее ему содержание лейкоцитов Q1=2.6·109/л.
Решим задачу Коши. Подставив значения t0=0 и Q0=9.6·109/л в аналитическое выражение (4), находим, что численные значения постоянной интегрирования с=9.6·109/л.
Замечание 1. В целях краткости изложения в дальнейшем размерность единиц будем опускать.
Применив результаты дополнительных условий Q1=2.6 и t1=46 и значения постоянной С=9.6, находим, что
Применив к равенству (5) логарифмирование и выполнив очевидные алгебраические преобразования, находим, что k=-0,028. Подставив в (4) значение постоянной интегрирования С=9.6 и коэффициент k=-0.028, находим, что
Найденный результат - аналитическое выражение (6) есть интегральная кривая связи между содержанием лейкоцитов и численными значениями хрональных характеристик анализов.
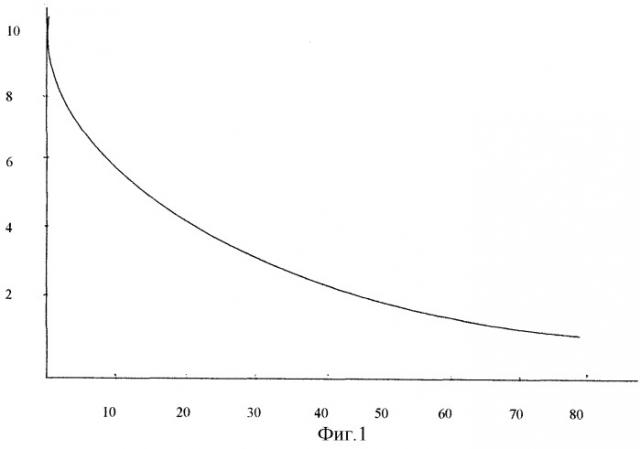
Выполним проверку модели (6). Известно, что 6.09.02 при продолжающемся курсе азатиоприна у больного З. взят анализ крови. В результате анализа найдено, что количество лейкоцитов в крови равно 1.2·109/л. Нетрудно вычислить, что 6.09.02 соответствует значение t=61 день. Подставив численное значение t=61 в равенство (6), находим, что Q=1.7·109/л. То есть предсказанное значение количества лейкоцитов Q=1.7 отличается от найденного в результате анализа Q=1.2 на 1.7-1.2=0.5. Известно, что ±0.5·109/л - точность результатов анализа. Следовательно, результаты выполненного применения модели (4) прогноза в точности совпадают с результатами анализа. На фиг.1 изображено изменение числа лейкоцитов крови при терапии азатиаприном.
Применив известное численное значение характеристики точности результатов метода определения содержания лейкоцитов, найдем значения характеристик Δ-коридора, определяющего область устойчивых решений уравнения (1). По мнению авторов, решение задачи о точном вычислении границ области существования допустимых решений требует отдельного исследования, выходящего за рамки данной работы. Поэтому ограничимся решением задачи о вычислении приближенных границ. Будем называть такое решение тривиальным.
Перепишем аналитическое выражение (6), учитывая точность измерения количества лейкоцитов крови
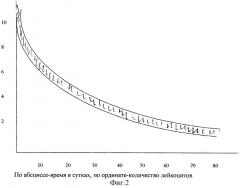
Аналитическими выражениями (7) записаны границы Δ-коридора значений лейкоцитов, учитывающего точность результатов измерений. Иначе говоря, при практической оценке содержания лейкоцитов следует принимать во внимание, что множество интегральных кривых, являющихся частными решениями, заключено в интервале, ограниченном кривыми, записанными аналитическими выражениями (7). Графическая интерпретация найденных результатов напечатана на фиг.2 в виде графиков функций (7).
Применив известную аксиому о не отрицательности количественной меры, приходим к заключению, что количество лейкоцитов не может быть отрицательным, т.е. Q≥0. Вследствие этого отрицательные значения величины Q, найденные применением формулы (7), отбрасываются. Очевидно, что множество интегральных кривых, принадлежащих обозначенному Δ-коридору, суть не пересекающиеся кривые. Следовательно, каждое решение единственно. Однако вследствие того, что значения результата измерения, находящегося в границах Δ-коридора, есть случайная величина с неизвестным законом распределения, возможны колебания результатов анализов в границах Δ-коридора. Иначе говоря, при практическом применении модели (1) результатом измерения может оказаться не точное решение (4) уравнения (2), а возмущенное решение.
где g(t, x) - ограниченная Δ-коридором случайная функция случайного аргумента, функция возмущения. Методы нахождения законов распределения изложены в работах [4], [5].
Применим модель (1) к решению задачи об изменении концентрации тромбоцитов и эритроцитов сыворотки крови того же больного. Клиническим анализом крови найдено, что 9 июля 2002 г. содержание тромбоцитов и эритроцитов в сыворотке крови больного было равно соответственно 242·109/л и 4.5·1012/л. В повторном анализе крови, выполненном 3 сентября 2002 г., уровень тромбоцитов и эритроцитов был равен соответственно 120·109/л и 2.14·1012/л. (Данные взяты из вышеуказанных историй болезни.) Ошибка метода при измерении числа тромбоцитов ±45·109/л, эритроцитов ±0.2·1012/л. Выполнив вычисления применением результатов модели (4), находим, что значение постоянной интегрирования С1=242 для тромбоцитов и С2=4.5 для эритроцитов. Значение коэффициента k соответственно: k1=-0.012, k2=-0.013. В результате расчетов находим, что прогнозируемая концентрация тромбоцитов Q1=116·109/л, Q2=2.03·1012/л для эритроцитов. Результаты анализов, выполненных 6.09.02, показали, что Q1=152·109/л, Q2=1.92·1012/л, т.е. разности между результатами прогноза и анализа для тромбоцитов Δ1=36, для эритроцитов Δ2=0.11. Найденные разности доказывают, что точность результатов прогнозов не выходит за границы Δ-коридоров.
Результаты работы внедрены в клиническую практику Городской многопрофильной больницы №2 и Александровской больницы, клиническое применение полностью подтверждает адекватность найденной модели. Результаты апробации модели, выполненной на 22 пациентах с миастенией Gravis с II-IV классом заболевания [6], 5 пациентах с идеопатической воспалительной миопатией и 1 пациенте с хронической воспалительной демиелинизирующей полиневропатией, являются свидетельством в пользу того, что точность модели - вероятность ошибки первого рода не превосходит 0.05.
Таким образом:
1) Впервые найдена математическая модель, применение результатов которой позволяет выполнить временной прогноз изменения содержания форменных элементов крови: лейкоцитов, тромбоцитов, эритроцитов и вычислить прогноз развития гипоплазии кроветворения.
2) Доказана правильность найденной модели и области ее применения, что подтверждено клиническим испытанием: применение результатов моделирования к диагностике и лечению. Результаты апробированы на базе Городской Многопрофильной Больницы №2 и Александровской больницы.
3) Доказано, что применение способа прогнозирования побочных эффектов при цитостатической терапии на основании метода математического моделирования позволяет значительно уменьшить количество результатов измерений, находимых опытным путем для нахождения законов изменения количеств форменных элементов крови.
4) По мнению авторов, предложенный способ может быть применен в целях решения фундаментальных задач гематологии.
Предложенный способ прогнозирования побочных эффектов при цитостатической терапии может быть применен также при решении прикладных задач гематологии - задач идентификации и прогноза. А также в решении задач теоретической и прикладной неврологии. А именно, при решении задач прикладной неврологии применение найденной модели позволяет проводить патогенетическую терапию с возможностью предупреждения лейкопении. Иначе говоря, предложен способ, позволяющий вывести лечение на уровень рациональной терапии, удовлетворяющей современным требованиям доказательной медицины.
Способ прогнозирования развития гипоплазии кроветворения при цитостатической терапии больных иммуноопосредованными заболеваниями нервной и мышечной систем, включающий клинический анализ крови, отличающийся тем, что у больного определяют количество форменных элементов крови до начала лечения и повторно в процессе лечения, на основании полученных данных, по формуле
Q=Q0еkt,
где Q - количество форменного элемента крови;
Q0 - количество форменного элемента крови до начала лечения;
t - длительность цитостатической терапии, в днях,
принимая, что
Q=Q1,
где Q1 - количество форменных элементов крови при повторном анализе,
t=t1,
где t1 - длительность цитостатической терапии до повторного анализа крови, в днях,
определяют коэффициент пропорциональности k, зависящий от индивидуальных свойств организма больного, и, используя полученные значения Q0 и k, по формуле для расчета Q определяют срок прогнозируемого развития гипоплазии кроветворения.