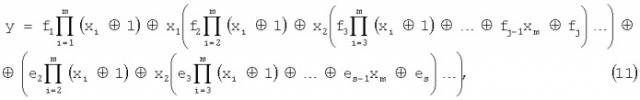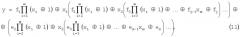Способ запоминания цифровой информации

Способ запоминания цифровой информации

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой вычислительной техники и может быть использовано для запоминания цифровой информации.

Способ, описанный в настоящей заявке, может применяться в вычислительных системах с программируемыми логическими интегральными схемами (ПЛИС). В таких схемах может изменяться структура связей между логическими элементами, что обеспечивает возможность схемотехнической реализации различных логических функций. Совокупность комбинаций таких связей позволяет запоминать и хранить большие объемы цифровой информации.

Известен способ запоминания цифровой информации, заключающийся в том, что по заданному адресу выбирается определенная ячейка памяти, в которой затем запоминается цифровая информация (Алексеенко А.Г., Шагурин И.И. Микросхемотехника. Учеб. пособие для вузов. / Под ред. И.П.Степаненко. - М.: Радио и связь, 1982, стр.246).

Недостатком этого способа является большое число ячеек памяти и большие аппаратные затраты, необходимые для запоминания большого объема информации, поскольку для запоминания одного бита информации требуется одна ячейка памяти.

Наиболее близким к предлагаемому способу является способ запоминания цифровой информации (прототип), заключающийся в том, что при записи запоминаемой информации строится функция, параметры которой устанавливают в зависимости от запоминаемой информации, информация хранится в виде схемотехнической реализации построенной функции, и при считывании запоминаемая информация восстанавливается по значениям этой функции [Кохонен Т. Ассоциативные запоминающие устройства: Пер. с англ. - М.: Мир, 1982, стр.39-45].

Недостатком этого способа являются большие схемотехнические затраты при запоминании большого объема цифровой информации, так как сложность схемотехнической реализации построенной функции может быть большой.

Цель изобретения - уменьшение схемотехнических затрат и, тем самым, увеличение объема запоминаемой цифровой информации за счет запоминания цифровой информации в ПЛИС в виде минимизированной булевской логической функции.

Для достижения цели предложен способ, заключающийся в том, что при записи запоминаемой информации строится функция, параметры которой устанавливают в зависимости от запоминаемой информации, информация хранится в виде схемотехнической реализации построенной функции, и при считывании запоминаемая информация восстанавливается по значениям этой функции. Новым является то, что по запоминаемой информации строится булевская логическая функция в совершенной нормальной дизъюнктивной форме, аргументом которой является адрес запоминаемой информации, а значением является запоминаемая информация, затем булевская логическая функция преобразуется в форму многочлена Жегалкина, далее минимизируется число элементарных булевских операций, входящих в многочлен Жегалкина, и затем минимизированный многочлен Жегалкина реализуется на программируемой логической интегральной схеме.

Предлагаемый способ запоминания цифровой информации реализуется следующим образом.

При записи информации по запоминаемой цифровой информации строится булевская логическая функция в совершенной нормальной дизъюнктивной форме (СНДФ), значения которой равны битам запоминаемой информации. При задании последовательных величин аргумента булевской функции ее значения будут равны запоминаемой информации. Для этого запоминаемая цифровая информация представляется в виде таблицы истинности. Таблица истинности (табл.1) булевской логической функции состоит из двух столбцов. В левом столбце располагаются адреса памяти или значения двоичного m-разрядного аргумента или переменной х₁x₂x₃...x_m булевской функции, а в правом - биты запоминаемой цифровой информации или значения булевской логической функции y=f(x₁x₂x₃...x_m)=0,1.

Булевская логическая функция строится в СДНФ (1) в следующем порядке. Записывается дизъюнкция конъюнкций всех разрядов аргумента булевской функции для тех значений аргумента, при которых булевская логическая функция согласно таблице истинности принимает значение 1. Затем ставится знак инверсии над теми разрядами аргумента, которые равны 0 в таблице истинности.

Таблица 1
x1x2x3...xm	y
000...0	f(000...0)
100...0	f(100...0)
010...0	f(010...0)
111...1	f(111...1)

Далее булевская логическая функция преобразуется к форме многочлена Жегалкина

где а_i=0,1, i=1...n, n=2^m - максимально возможное число конъюнкций в многочлене Жегалкина от m переменных, а ⊕ - операция суммирования по модулю два.

Для этого преобразования все операции дизъюнкции и инверсии в уравнении (1) заменяются на операции сложения по модулю два и конъюнкции согласно формул

и затем приводятся подобные члены.

В многочлене Жегалкина (2) от m независимых входных переменных x₁x₂x₃...x_m содержится не более n=2^m конъюнкций входных переменных, соединенных операцией суммирования по модулю два. Количество элементарных булевских операций, входящих в многочлен Жегалкина (2), будет не более 2^m-1<n операций сложений по модулю два и не более

операций логического умножения, а значит, всего не более n₁=(m+2)·n/2 элементарных булевских операций.

Далее многочлен Жегалкина минимизируют по количеству входящих элементарных булевских операций. Заметим, что многочлен Жегалкина, содержащий всевозможные конъюнкции (а_i=1, i=1...n), тождественно равен конъюнкции всех переменных, взятых с инверсией, то есть

Процедура минимизации многочлена Жегалкина заключается в следующем.

Шаг 1. Сначала подсчитаем число элементарных булевских операций n₁ в многочлене Жегалкина (2).

Затем сделаем тождественное преобразование многочлена Жегалкина (2)

где b_i=а_i⊕1, i=1...m.

Подсчитаем число элементарных булевских операций n₂ в выражении (7). Если n₁≤n₂, то многочлен Жегалкина (2) остается без изменения, иначе многочлен (2) заменяем тождественным выражением (7).

Поскольку n₁+n₂=(m+2)·n/2, а выбирается min{n₁,n₂}, то полученное в результате выражение (2) или (7) будут содержать не более n₃=(m+2)·n/4 элементарных булевских операций.

Шаг 2. Затем либо члены оставшегося без изменения многочлена Жегалкина (2), либо многочлена Жегалкина, входящего в выражение (7) вида

разделим на две группы или два новых многочлена Жегалкина. В первом многочлене Жегалкина y2 сгруппируем члены, в которые входит множитель x₁ (или x₂, х₃,...), а во втором многочлене Жегалкина y3 - члены, в которые не входит множитель x₁.

При выносе общего множителя x₁ в многочлене (9) количество элементарных булевских операций уменьшается на число дизъюнкций в этом многочлене.

Шаг 3. Процедура минимизации многочлена Жегалкина заканчивается, когда многочлены Жегалкина типа (9) и (10) будут содержать не более одного члена, иначе переходим к шагу 1 процедуры минимизации для многочленов (9) и (10).

После окончания процедуры минимизации получим многочлен следующего вида

где f_i,е_i=0,1.

При выполнении шагов 1 и 2 процедуры минимизации количество элементарных булевских операций уменьшается вдвое по сравнению с их максимально возможным числом для данного числа независимых переменных многочлена Жегалкина, однако при этом число многочленов Жегалкина удваивается.

Из выражения (11) рекуррентные соотношения для количества элементарных булевских функций S_m при выполнении процедуры минимизации запишутся

отсюда

Значит, после окончания процедуры минимизации через m-1 шагов будем иметь

Поэтому количество элементарных булевских операций после минимизации можно оценить величиной

Таким образом, для запоминания n бит информации используется минимизированная булевская функция, для реализации которой требуется не более порядка O(n) элементарных булевских операций.

Затем выполняется схемотехническая реализация минимизированной булевской функции, например, на ПЛИС, как это описано в Кнышев Д.А., Кузелин М.О. ПЛИС фирмы «XILINX»: описание структуры основных семейств. - М.: Издательский дом «Додэка-XXI», 2001.

Для запоминания n бит информации ПЛИС должна позволять реализовывать булевскую логическую функцию с O(n) элементарными булевскими операциями. Критерием окончания процедуры минимизации булевской логической функции может быть также получение многочлена Жегалкина с O(n) и менее элементарными булевскими операциями.

Сложность схемотехнической реализации элементарной булевской операции примерно соизмерима со сложностью реализации одной ячейки памяти, однако в известном способе дополнительно требуется дешифрация этой ячейки памяти. Поэтому, если сложность схемотехнической реализации предлагаемого способа запоминания цифровой информации имеет порядок O(n), то сложность схемотехнической реализации способа, при котором информация запоминается в ячейках памяти, имеет порядок O(m·n), так как для реализации одной ячейки памяти требуется 1 элементарная булевская функция и для реализации дешифратора этой ячейки памяти - m-1 элементарных булевских функций. Поскольку O(n)<<O(m·n), то предлагаемый способ проще.

В качестве примера рассмотрим случай, когда запоминается 16 бит информации 1010011100101101. Эта информация адресуется 4 независимыми булевскими переменными и таблица истинности для нее представлена таблицей 2. Булевская логическая функция в СНДФ запишется

Используя формулы (3) после приведения подобных членов, получим многочлен Жегалкина

содержащий 21 элементарную булевскую операцию.

Минимизируем этот многочлен. Поскольку число членов в многочлене Жегалкина равно 11, то есть больше 16/2=8, то представим многочлен Жегалкина в виде

Таблица 2
x1x2x3x4	y
0000	1
1000	0
0100	1
1100	0
0010	0
1010	1
0110	1
1110	1
0001	0
1001	0
0101	1
1101	0
0011	1
1011	1
0111	0
1111	1

Количество элементарных булевских операций в последнем выражении равно 13. Преобразуем его согласно процедуры минимизации к следующей форме

содержащей уже 10 элементарных булевских операций.

Таким образом, для запоминания заданных 16 бит информации требуется схемотехническая реализация всего 10 элементарных булевских операций, что существенно меньше, чем необходимо для реализации 16 ячеек памяти и дешифратора на эти ячейки памяти (64 элементарные булевские операции).

С увеличением объема запоминаемой цифровой информации выигрыш в схемотехнических затратах на реализацию предлагаемого способа возрастает.

В предлагаемом способе цифровая информация объемом n бит запоминается в ПЛИС в виде минимизированной булевской логической функции, схемотехническая сложность которой составляет для любой запоминаемой информации не более O(n) элементарных булевских операций, что существенно меньше схемотехнической сложности порядка O(m·n) запоминания цифровой информации в отдельных ячейках памяти. Например, схемотехнические затраты при реализации памяти объемом 1 Гбайт могут быть уменьшены примерно в 30 раз. Кроме того, схемотехническая сложность зависит от конкретного вида информации, и для информации, которой соответствуют простые булевские функции, будет весьма незначительной, но в любом случае не будет превосходить величины O(n).

Достигаемым техническим результатом предлагаемого способа является уменьшение схемотехнических затрат на запоминание цифровой информации.

Способ запоминания цифровой информации, заключающийся в том, что при записи запоминаемой информации строится функция, параметры которой устанавливают в зависимости от запоминаемой информации, информация хранится в виде схемотехнической реализации построенной функции и при считывании запоминаемая информация восстанавливается по значениям этой функции, отличающийся тем, что по запоминаемой информации в вычислительной системе строится булевская логическая функция в совершенной нормальной дизъюнктивной форме, аргументом которой является адрес запоминаемой информации, а значением является запоминаемая информация, затем булевская логическая функция преобразуется в форму многочлена Жегалкина, далее минимизируется число элементарных булевских операций, входящих в многочлен Жегалкина, и затем минимизированный многочлен Жегалкина реализуется на программируемой логической интегральной схеме.