Способ получения энергии и устройство для его реализации

Способ получения энергии и устройство для его реализации

Иллюстрации

Показать все

Реферат

Изобретение относится к области теоретической физики и предназначено для получения энергии в беззатратных процессах взаимодействия статического насыщающего магнитного поля постоянных магнитов с движущимся в этом поле ферромагнитным веществом, обладающим свойством магнитной вязкости.

Магнетизм - особая форма взаимодействия электрических токов и магнитов (тел с магнитным моментом) между собой и одних магнитов с другими магнитными материалами. Магнитное взаимодействие пространственно разнесенных тел осуществляется через магнитное поле Н, которое, как и электрическое поле Е, представляет собой проявление электромагнитной формы движения материи. Между магнитными и электрическими полями нет полной симметрии, так как источниками электрических полей являются электрические заряды, а магнитные заряды - монополи пока не обнаружены, хотя теория предсказывает их существование. Источник магнитного поля - движущийся электрический заряд, то есть электрический ток. В атомных масштабах движение электронов и протонов создает орбитальные микротоки, связанные с переносным движением этих частиц в атомах или атомных ядрах, кроме того, наличие у микрочастиц спина обусловливает существование у них спинового магнитного момента.

Поскольку электроны, протоны и нейтроны, образующие атомные ядра, атомы, молекулы и все макротела (газы, жидкости, кристаллические и аморфные твердые тела), имеют собственный магнитный момент, то, в принципе, все вещества подвержены влиянию магнитного поля - обладают магнитными свойствами, то есть являются магнетиками. Магнетики подразделяются на диамагнетики, парамагнетики и ферромагнетики. Последние имеют наибольшую магнитную восприимчивость и используются в технике в качестве эффективных магнитов. В них атомные магнитные моменты спонтанно коллинеарно самоориентируются, образуя аномально большие магнитные моменты. У лучших современных магнитных материалов энергетическое произведение (В Н)_max достигает величины 320 Тл·кА/м (40 млн Гс·Э), например, у материала с высокой коэрцитивной силой SmCo₃ (см., напр., Преображенский А.А., Биширд Е.Г. Магнитные материалы и элементы, 3 изд., М., 1986; Февралева И.Е., Магнитотвердые материалы и постоянные магниты. К., 1969; Постоянные магниты. Справочник, М., 1971).

Сложность атомной структуры веществ, построенных из огромного числа микрочастиц, дает практически неисчерпаемое разнообразие их магнитных свойств, связь которых с немагнитными свойствами (электрическими, механическими, оптическими и др.) позволяет использовать исследования магнитных свойств для получения информации о внутренней структуре и других свойствах микрочастиц и макротел. Отметим, что магниты обладают внутренней энергией. В случае однородного магнитного поля в объеме магнита V энергия запасенного магнитного поля W˜μ₀H²V/2, где μ₀=1,256·10^-6 Г/м - абсолютная магнитная проницаемость. Причем эта величина энергии практически не расходуется при силовых взаимодействиях с другими магнетиками и сохраняется благодаря постоянному движению заряженных микрочастиц вещества.

Источником энергии является само вещество магнитов, обладающее запасом магнитной энергии, который за счет процессов, происходящих на микроуровне (атомов и молекул вещества), непрерывно восполняется, а точнее, поддерживается на неизменном уровне, если не считать факторов, приводящих к так называемому старению магнитов. Кроме того, механическая энергия возникает в процессе движения ферромагнитовязкого вещества в пространственно локализованном насыщающем магнитном поле.

Известный принцип возрастания энтропии и первое и второе начала термодинамики оперируют с теплоэнергетическими преобразованиями, которые всегда (кроме состояния равновесия) идут с затратой энергии при совершении какой-либо работы, большей той, которая составляет саму проделанную работу, а часть затраченной энергии безвозвратно превращается в тепловую. Поэтому к.п.д. всех известных преобразователей энергии всегда меньше единицы. Однако в микромире действует иной процесс: движение микрочастиц обусловлено тепловой энергией - импульс р движения микрочастиц массой m₁ определяется как где k - постоянная Больцмана, - температура по шкале Кельвина, а соударения микрочастиц между собой вызывают тепловые процессы - среда нагревается, то есть происходит самовоспроизводящийся обмен энергией, при котором беспредметно говорить о тепловых потерях, поскольку тепловая энергия является источником движения микрочастиц, а это движение порождает саму тепловую энергию. Таким образом, на микроуровне взаимообратные процессы преобразования энергии, например тепловой и кинетической, происходят с к.п.д., равным единице, то есть самоподдерживаются непрерывно во времени. Это находит свое выражение в «вечном» существовании материи в различных ее формах и видах, состоящей из массовых частиц - атомов и молекул, находящихся в постоянном движении и взаимодействии как между собой, так и с различного рода внешними полями и силами. С другой стороны, на макроуровне в космических масштабах можно констатировать такую же устойчивость «вечного» существования Вселенной, в которой происходят процессы преобразования энергии, однако не приводящие к термодинамическому равновесию и так называемой «тепловой смерти» Вселенной.

Эти обстоятельства позволяют считать, что должны существовать способы беззатратного получения энергии, что соответствовало бы принципу уменьшения энтропии. Так, в работе автора [1] было показано, что при обнаружении явления сверхпрозрачности станет возможной передача электромагнитным полем энергии от более холодного тела к более горячему, что пока считается невозможным согласно современным представлениям термодинамики.

Для ферромагнетиков, подчиняющихся закону Кюри, существует так называемая критическая температура Θ, при которой магнитная восприимчивость оказывается сравнимой с единицей или даже становится меньшей единицы, и вещество становится из парамагнитного диамагнитным (закон Кюри-Вейсса), то есть магнитная восприимчивость зависит от действия различных факторов - температуры, величины напряженности магнитного поля, механического напряжения и некоторых других.

Одним из интересных свойств ферромагнитных материалов является их так называемая магнитная вязкость, магнитное последействие - отставание по времени намагниченности ферромагнетика от изменения напряженности магнитного поля. В наиболее простых случаях изменение намагниченности ΔJ в зависимости от времени t описывается формулой

где J₀ и J_∞ - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент t=0 и после установления нового равновесного состояния, τ - константа, характеризующая скорость процесса и называемая постоянной времени релаксации (магнитной вязкости). Значение τ зависит от природы магнитной вязкости и в различных материалах может изменяться от 10^-9 с до нескольких десятков часов. В общем случае для описания процесса последействия одного значения τ недостаточно.

Различают два вида магнитной вязкости: диффузионный (рихтеровский) и термофлуктуационный (иордановский). В первом из них магнитная вязкость определяется диффузией примесных атомов или дефектов кристаллической структуры. Объяснение роли примесей было дано J.Snock, а более строгая теория построена L.Neel и базируется на предположении о преимущественной диффузии примесных атомов в те межатомные промежутки кристалла, которые определенным образом ориентированы относительно направления спонтанной намагниченности. Это создает локальную наведенную анизотропию, приводящую к стабилизации доменной структуры. Поэтому после изменения магнитного поля новая доменная структура устанавливается не сразу, а после диффузного перераспределения примеси, а также, возможно, с учетом эффекта Баркгаузена (скачкообразное изменение намагниченности ферромагнетиков при непрерывном изменении внешних условий, например магнитного поля), что и является причиной магнитной вязкости.

Второй вид магнитной вязкости более универсален и наблюдается практически во всех ферромагнетиках, особенно в области магнитных полей, сравнимых с коэрцитивной силой. Неелем был предложен термофлуктуационный механизм для объяснения этого вида магнитной вязкости. Тепловые флуктуации способствуют преодолению доменными стенками энергетических барьеров в магнитных полях, меньших критического поля. В высококоэрцитивных сплавах, состоящих из однодоменных областей, наблюдается особенно большая магнитная вязкость, так как в этом случае термические флуктуации сообщают дополнительную энергию для необратимого вращения спонтанной намагниченности тех частиц, потенциальная энергия которых во внешнем магнитном поле недостаточна для их перемагничивания.

Кроме этих основных механизмов магнитной вязкости, существуют и другие. Например, в некоторых ферритах вклад магнитной вязкости дает перераспределение электронной плотности (диффузия электронов между ионами разной валентности). С магнитной вязкостью тесно связаны такие явления в ферромагнетиках, как потери на перемагничивание, временной спад относительной магнитной проницаемости μ и ее частотная зависимость (см., напр., Kronmüller H., Nachwirkung in Ferromagnetika, 1068; C.B.Вонсовский, Магнетизм, М., 1971; Д.Д.Мишин. Магнитные материалы, М., 1981).

Известное свойство магнитной вязкости ферромагнетиков использовано в заявляемом техническом решении.

Заявляемый способ получения энергии аналогов не имеет.

Заявляемый способ получения энергии состоит в том, что образуют на некотором промежутке пространства L насыщающее магнитное поле для ферромагнитовязкого вещества, которое продвигают в указанном промежутке пространства с некоторой скоростью V, величину которой согласуют с постоянной времени τ магнитной вязкости ферромагнитовязкого вещества, например, по формуле L/V≈2,8 τ, в результате чего получают механическую энергию вследствие возникающей силы, приложенной к ферромагнитовязкому веществу со стороны насыщающего магнитного поля и направленной коллинеарно вектору скорости V.

Заявляемый способ объясняется уменьшением с временным запаздыванием магнитной восприимчивости движущегося ферромагнитовязкого вещества, помещаемого в насыщающее магнитное поле, в результате чего втягивающая ферромагнитовязкое вещество сила от действия насыщающего магнитного поля оказывается больше силы торможения этого вещества магнитным полем на выходе промежутка взаимодействия. Интегрирование парциальных сил втягивания и торможения дифференциальных объемов dV ферромагнитовязкого вещества, находящегося в промежутке его активного взаимодействия с магнитным полем, по длине магнитного зазора определяет результирующую силу, приложенную к взаимодействующему с магнитным полем ферромагнитовязкому веществу, направленную вдоль вектора скорости V.

В качестве ближайшего аналога (прототипа) заявляемому техническому решению - устройству, реализующему заявляемый способ, является «Магнитовязкий маятник», известный из заявки того же автора №2005111823/28 (013701) от 20.04.2005, по которой выдан патент РФ на изобретение №2291546 (опубликован в бюллетене №1 от 10.01.2007). Экспертиза проведена в отделе измерительной техники и приборостроения ФИПС.

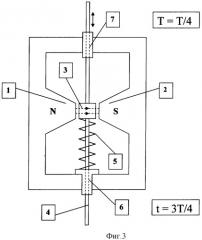
В устройстве-прототипе использован постоянный магнит с насыщающим магнитным полем для ферромагнитного тела из магнитовязкого материала, подвешенного на пружине и совершающего колебательное движение относительно магнитного зазора постоянного магнита, причем постоянная релаксации магнитной вязкости тела из ферромагнитного материала выбрана соизмеримой со временем пребывания ферромагнитного тела в насыщающем магнитном поле, например, с одной десятой периода свободных колебаний этого тела. Приведением внешними силами ферромагнитного маятника в движение в дальнейшем колебания маятника продолжаются неограниченно долго с определенными амплитудой и частотой без воздействия внешних сил. При этом возникающая кинетическая энергия маятника является результатом взаимодействия насыщающего магнитного поля постоянного магнита и движущегося ферромагнитовязкого вещества (см. фиг.3 и 4).

Недостатком известного устройства является относительно малая его энергетическая эффективность, обусловленная низкочастотностью механических колебаний.

Указанный недостаток устранен в заявляемом техническом решении.

Целью изобретения является повышение кинетической энергии, получаемой от взаимодействия движущегося ферромагнитовязкого вещества с насыщающим магнитным полем.

Указанная цель достигается в совокупности реализующих заявляемый способ получения энергии устройств, использующих принцип вращения ферромагнитного диска с осью вращения, выполненного из магнитовязкого вещества, кромка которого помещена в насыщающее магнитное поле постоянного магнита (свободного от источников питания) на некотором промежутке взаимодействия. Конструктивная реализация таких устройств отличается значительным разнообразием, в частности, выполнения профилей магнитных систем и их количества в одном устройстве. Ниже рассматривается базовая модель заявляемого технического решения - устройства, а также различные ее модификации.

Устройство, содержащее постоянный магнит и взаимодействующее с ним ферромагнитовязкое вещество, отличающееся тем, что ферромагнитовязкое вещество выполнено в виде диска радиуса R, связанного с осью его вращения, кромка диска помещена в локализованное в пространстве длиной L по касательной к диску насыщающее магнитное поле постоянного магнита, при этом запуск устройства в работу осуществлен однократным приложением к диску достаточного для пуска устройства момента импульса от внешнего источника, а постоянная времени магнитной вязкости τ ферромагнитовязкого вещества выбрана из условия τ=0,36L/ω₀R, где ω₀ - значение угловой скорости диска, соответствующее максимуму его вращательного момента.

Поставленная цель в заявляемом техническом решении достигается благодаря замен» колебательного движения некоторой массы ферромагнитного тела на ее вращательное движение и является следствием отставания в динамике вращательного движения ферромагнитовязкого диска его магнитного «центра тяжести» размещенной в поле постоянного магнита части ферромагнитовязкого диска в каждый произвольный момент времени от центра притяжения постоянного магнита, что создает тангенциальную силу тяготения со стороны постоянного магнита, приложенную к краевой части ферромагнитного диска, в результате чего возникает вращательный момент, поддерживающий вращательное движение ферромагнитовязкого диска угловой скоростью, определяемой постоянной релаксации магнитной вязкости ферромагнитовязкого вещества диска. В случае однородного магнитного поля в зазоре между полюсами постоянного магнита реализуется так называемый «жесткий режим» самовозбуждения вращательного движения, при котором необходимо принудительно (под действием внешних сил) привести ферромагнитовязкий диск во вращательное движение с необходимой угловой скоростью. По мере достижения указанной угловой скорости магнитный «центр тяжести» части ферромагнитовязкого диска, связанной с магнитным полем постоянного магнита, смещен относительно центра тяготения поля постоянного магнита и эта величина смещения между указанными центрами определяет постоянно действующий вращательный момент, уравновешиваемый величиной момента трения (нагрузочного момента) в оси диска. Отставание магнитного «центра тяжести» вышеуказанной части ферромагнитовязкого диска от центра притяжения магнитного поля постоянного магнита определяется магнитной вязкостью, при которой дифференциальные объемы указанной части ферромагнитовязкого диска, более длительное время находящиеся в насыщающем магнитном поле постоянного магнита, в большей степени уменьшают свою магнитную восприимчивость, чем дифференциальные объемы, магнитное насыщение в которых еще не наступило. Это создает перераспределение в указанной части ферромагнитовязкого диска величин магнитной восприимчивости, градиент которой направлен противоположно к вектору действующей на ферромагнитовязкий диск силы со стороны магнитного поля постоянного магнита. В такой системе магнитное поле постоянного магнита является статическим, а роль его временного изменения в тангенциальном направлении (как известное условие движения [2]) выполняют краевые участки ферромагнитовязкого диска с переменными параметрами магнитной восприимчивости, то есть система является параметрическим генератором вращательного движения. Замена колебательного движения ферромагнитовязкой массы на ее вращательное движение в заявляемом техническом решении энергетически более эффективна, так как можно использовать достаточно быстрое вращение этой массы, повышая тем самым кинетическую энергию последней.

Заявляемое техническое решение (способ и реализующие его устройства) будет понятно из представленных чертежей.

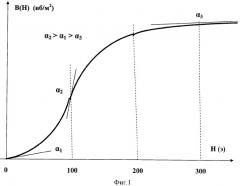
На фиг.1 представлен график зависимости магнитной индукции В в ферромагнетике от напряженности Н внешнего магнитного поля, при некотором значении которой в ферромагнетике возникает насыщение (на данном графике этот участок насыщающего магнитного поля соответствует диапазону напряженностей 200-300 эрстед).

На фиг.2 приведен соотнесенный к фиг.1 график зависимости магнитной восприимчивости χ ферромагнетика от напряженности Н приложенного к нему магнитного поля. Видно, что при Н=0 величина магнитной восприимчивости относительно невелика и имеет конечное значение. С ростом напряженности поля она также растет до максимальной величины (при Н*=100 Э), а затем снова падает и может иметь при этом весьма малые значения (это - так называемая кривая Столетова).

На фиг.3 приведена схема устройства-прототипа - магнитовязкого маятника, содержащая постоянный магнит с его полюсами 1 и 2, между которыми размещен образец ферромагнитовязкого вещества 3 на скользящей оси 4, задающей одну степень свободы для движения образца 3, подвешенного на пружине 5, другой конец которой связан с неподвижным постоянным магнитом, а скольжение оси 4 происходит во втулках 6 и 7 с малым трением.

На фиг.4 графически представлены гармоническое колебательное движение ферромагнитовязкого образца 3 (фиг.3) - пружинного маятника и силовое воздействие на этот образец со стороны магнитного поля постоянного магнита. Видно, что действие магнитной вязкости ферромагнетика снижает тормозящую силу выходящего по инерции из магнитного зазора образца и увеличивает силу его втягивания в магнитный зазор при обратном ходе образца в каждом полупериоде его колебаний. Сила торможения имеет максимум, меньший, чем максимум силы втягивания вследствие уменьшения величины магнитной восприимчивости ферромагнетика, пока он находится в насыщающем магнитном поле, и в результате увеличения величины магнитной восприимчивости ферромагнетика, пока он движется в свободном пространстве до верхней или до нижней «мертвых» точек в соответствующих полупериодах колебаний.

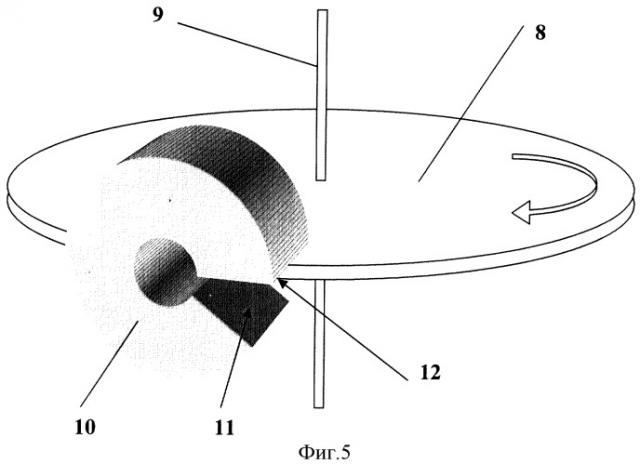
На фиг.5 показано устройство в упрощенном виде, состоящее из вращающегося ферромагнитовязкого диска 8 с осью вращения 9 и постоянного магнита 10 с полюсами 11 и 12, образующими магнитный зазор, в который введен край диска 8. Магнитное поле в зазоре в его определенной части выбрано насыщающим для ферромагнитовязкого вещества диска 8.

На фиг.6 приведена базовая модель ферромагнитовязкого двигателя, содержащая ферромагнитовязкий диск 8 с осью вращения 9, помещенный в магнитное поле статора 10 из четырех полюсных пар 11 (12) (число их может быть произвольным), в зазорах которых, лежащих в одной плоскости, размещена кромка диска 8. Указаны геометрические параметры полюсных пар 11 (12) и диска 8, обозначены направление и величина угловой скорости вращения диска 8.

На фиг.7 дана развертка статора 10 магнитной системы в обозначениях базовой модели устройства (фиг.6) с помещенной в зазоры полюсных пар 11 (12) кромкой диска 8 из ферромагнитовязкого вещества и обозначено направление движения последнего.

На фиг.8 представлен график мгновенного (в любой произвольный момент времени) распределения величины магнитной восприимчивости ферромагнитовязкого вещества кромки диска, находящейся в насыщающем магнитном поле зазора и у его краев с учетом оптимального движения этого вещества вдоль магнитного зазора, обусловленного вращением диска. В рабочей зоне длиной L магнитного зазора насыщающее магнитное поле приводит к экспоненциальному уменьшению величины магнитной восприимчивости, а по выходе из зазора магнитная восприимчивость вновь восстанавливается экспоненциально, стремясь к величине, соответствующей действующему вне магнитного зазора магнитному полю.

На фиг.9 показана развертка двухкомпонентного статора ферромагнитовязкого двигателя (без диска). Основной компонентой такого статора является полюсная пара, создающая насыщающее магнитное поле в ферромагнитовязком веществе диска (300 Э на фиг.2) и имеющая минимальный по высоте зазор. Другой компонентой такого статора является полюсная пара с большим зазором, создающая магнитное поле, соответствующее максимуму магнитной восприимчивости ферромагнитовязкого вещества (100 Э на фиг.2).

На фиг.10 представлена эпюра напряженности магнитного поля в соответствующих магнитных зазорах двухкомпонентного статора двигателя, рассмотренного на фиг.9 (на фиг.2 имеем Н_max=300 Э, Н*=100 Э).

На фиг.11 дан график распределения магнитной восприимчивости вдоль координаты х развертки двухкомпонентного статора (фиг.9), соответствующий эпюре напряженности магнитного поля в зазорах такого статора (фиг.10) для случая неподвижного диска. Расстояния δх отражают зоны действия краевых эффектов насыщающего магнитного поля.

На фиг.12 представлено распределение величины относительной магнитной восприимчивости ферромагнитовязкого вещества в динамике вращения диска с квазиоптимальной угловой скоростью ω=ω₀=0,36L/Rτ относительно магнитного зазора с насыщающим магнитным полем Н_max. Видно, что восстановление магнитной восприимчивости по выходе ферромагнитовязкого вещества из зазора происходит достаточно быстро, поскольку согласно (1) процесс восстановления задан величиной χ_max, соответствующей максимуму магнитной восприимчивости (при Н*=100 Э на фиг.2), что увеличивает величину импульса торможения диска.

На фиг.13 изображена весовая функция G(x), принимающая значения от +1 до -1 при расчете сил втягивания и торможения ферромагнитовязкого диска магнитным полем в динамике его вращения. Эта функция показывает, что в центре магнитного притяжения магнитной полюсной пары (для однородного магнитного поля этот центр находится в середине длины L магнитного зазора) она не оказывает силового воздействия вдоль направления движения ферромагнитовязкого вещества на элемент его объема, находящийся в центре магнитного притяжения.

На фиг.14 представлена развертка конструкции трехкомпонентного статора двигателя (без диска), которая отличается от двухкомпонентной конструкции (фиг.9) введением после рабочего зазора с насыщающим магнитным полем полюсной пары с наклонными плоскостями, внутри которой образовано возрастающее неоднородное магнитное поле по координате х. Это позволяет существенно ослабить момент торможения диска, поскольку магнитная восприимчивость ферромагнитовязкого вещества по выходе его из зазора с насыщающим магнитным полем стремится к величине, меньшей максимальной, равной χ(Н_min)<χ_max(Н*).

На фиг.15 дано распределение величины относительной магнитной восприимчивости χ(х)/χ_max по координате х внутри зазора с насыщающим магнитным полем и за его пределами для трехкомпонентного статора (фиг.14). Видно, что при использовании трехкомпонентной структуры статора снижается фактор торможения диска.

На фиг.16 представлена модифицированная структура статора (развертка), соответствующая его трехкомпонентной структуре и образующая неоднородное магнитное поле, которое от малой величины напряженности Н_min экспоненциально возрастает до Н* и далее до Н_max и в пределах Н*<H≤Н_max становится насыщающим с протяженностью L вдоль оси х.

На фиг.17 дано распределение χ(х)/χ_max при выполнении статора по схеме фиг.16, из которого видно, что кривая χ(х) обладает более плавными переходами и максимальной эффективностью по критерию отношения сил втягивания и торможения. Поскольку магнитное поле в рабочей области неоднородно, то положение магнитного центра притяжения смещено вправо по оси х относительно центра длины L (показан пунктирной линией в заштрихованном прямоугольнике).

На фиг.8, 12 и 17 угловая скорость вращения диска ω, его радиус R, длина магнитного зазора L и постоянная времени магнитной вязкости τ связаны соотношением τ=0,40L/ωR, задающим квазимаксимум вращательного момента ферромагнитовязкого двигателя при заданных параметрах χ_max(H*), χ_min(H_max), H_min, Н_max и числе n полюсных пар статора двигателя.

На фиг.18 представлены: семейство относительных значений сил, действующих на элементы объема dV ферромагнитовязкого вещества в зазоре постоянного магнита с насыщающим магнитным полем, и характеристика М_вращ оптимизированного ферромагнитовязкого двигателя с подключенными к нему различными нагрузками от холостого хода до критической. Эти нагрузочные характеристики - суть прямые, проведенные из начала координат под разными углами к оси абсцисс ω. Точка пересечения кривой М_вращ с нагрузочной прямой определяет устойчивое состояние системы при угловой скорости вращения ферромагнитовязкого диска ω_раб>ω₀=L/2,806 Rτ. В частности, при угловой скорости ω_о вращения диска достигается максимум вращательного момента МахМ_вращ.

Рассмотрим сущность заявляемого технического решения.

Из общей теории создания генерирующих систем известно, что условием генерирования является построение четырехполюсника с отрицательным сопротивлением, например, как это имеет место в генераторе на туннельном диоде, вольтамперная характеристика которого в рабочей зоне имеет спад тока при росте приложенного к диоду напряжения. Роль такого «отрицательного сопротивления» в данном техническом решении выполняет ферромагнетик при его магнитном насыщении. Зависимость магнитной индукции В от напряженности магнитного поля Н (фиг.1) характеризуется переменной крутизной dB/dH˜χ(Н) (фиг.2) и в области насыщения кривая χ(Н) имеет спад магнитной восприимчивости ферромагнетика при росте напряженности, то есть dχ(H)/dH<0. Это позволяет создать неуравновешенную по силовому воздействию на ферромагнитное вещество со стороны насыщающего магнитного поля систему на основе соблюдения двух условий: ферромагнитное вещество должно обладать свойством магнитной вязкости и двигаться в насыщающем поле с определенной скоростью, согласованной с постоянной времени магнитной вязкости. Рассмотрим, как эти два условия позволяют обеспечить безостановочное вращение ферромагнитовязкого диска, кромка которого помещена в насыщающее магнитное поле постоянного магнита (фиг.5 и фиг.6). В базовой модели заявляемого устройства (фиг.6) полюсная пара 4 постоянного магнита-статора 3 двигателя, схематически представленная на фиг.7, создает на ее длине L однородное насыщающее магнитное поле. Движение в таком поле ферромагнитовязкого вещества (кромки диска 1) со скоростью V=ωR, где ω - угловая скорость диска, R - его радиус (до средней части кромки диска), приводит к распределению величины магнитной восприимчивости χ(х) в любой произвольный момент времени, как это представлено на фиг.8. Такое распределение по координате х вдоль длины L полюсной пары с совмещением начала координат с центром магнитного тяготения, положение которого при однородном магнитном поле совпадает с центром полюсной пары, то есть на расстоянии L/2 от краев полюсной пары, происходит из-за того, что входящая в магнитный зазор масса ферромагнетика под действием насыщающего магнитного поля Н_max>Н* уменьшает свою намагниченность J(t) по экспоненциальному закону согласно (1), то есть по экспоненциальному закону будет изменяться магнитная восприимчивость χ(t)=J(t)/μ_оН ферромагнетика с учетом постоянной времени τ магнитной вязкости по закону:

где χ(Н_max)_∞ - магнитная восприимчивость в насыщающем магнитном поле с напряженностью Н_max в установившемся режиме (за большой промежуток времени), Δχ=χ_max-χ_min - изменение магнитной восприимчивости за интервал времени Δt=L/V. При этом χ_max соответствует напряженности магнитного поля Н*, a χ_min - полю с напряженностью Н_max, а также имеет место связь из чего следует, что за время Δt=L/V величина магнитной восприимчивости χ_min(Δt)>χ(H_max)_∞.

Центр магнитного притяжения полюсной магнитной пары (фиг.8) ферромагнетика в начале координат х=0 разделяет находящуюся в магнитном поле этой полюсной пары кромку диска из ферромагнитовязкого вещества на две части - втягивающуюся в магнитный зазор в промежутке - L/2≤х≤0 и тормозящую диск часть в промежутке 0≤х≤+L/2. Поскольку соответствующие силы пропорциональны магнитной восприимчивости χ(х), то обеспечение максимума вращательного момента диска требует определения скорости его вращения ω_о в магнитном зазоре из уравнения (без учета функции веса G(x)):

в котором t=х/ω_оR. Решение уравнения (3) имеет вид Δt/τ=2 ln(Δt/τ+1), откуда находим искомое отношение Δt/τ=2,513, где Δt=L/ω_оR. При этом, задаваясь при х=-L/2 значением χ(-L/2)/χ_max=1, получим при х=0 отношение χ(0)/χ_max=0,285, а при х=L/2 оно равно χ(+L/2)/χ_max=0,081. С учетом функции G(x) как множителя в (3) перед членом ехр(-t/τ) оптимальное значение отношения Δt/τ будет определяться как Δt/τ=2,8059 (получено вариационным расчетом на ПК с применением программы Excel без учета краевых эффектов на промежутках δх фиг.12 и 13).

После выхода ферромагнитовязкого вещества из магнитного зазора полюсной пары магнитная восприимчивость χ вновь начинает возрастать экспоненциально, стремясь к величине χ(Н), соответствующей магнитному полю Н(х) при х>L/2, которое существенно меньше H_max.

Расстояние между смежными полюсными парами 11 (12) статора 10 (фиг.6) таково, что на этом пути магнитная восприимчивость полностью восстановится (то есть увеличится) до уровня, соответствующего значению χ(-L/2), так что взаимодействие ферромагнитовязкого диска с насыщающим магнитным полем Н_max в этой следующей по ходу вращения диска 8 магнитной паре вновь повторится по рассмотренному выше алгоритму. При этом эффективность двигателя (его мощность) пропорциональна числу n используемых в нем полюсных пар.

Повышение величины Δχ целесообразно и обеспечивается, если напряженность магнитного поля у входа магнитного зазора при х≤-L/2 (фиг.8) будет равна Н*, при котором максимальна магнитная восприимчивость (χ_max). Это условие выполняется в модифицированном устройстве двухкомпонентного статора двигателя, развертка которого показана на фиг.9. В рабочем зазоре длиной L действует магнитное поле с напряженностью Н_max, а в смежных магнитных зазорах - с напряженностью Н*. Эпюра распределения напряженности показана на фиг.10. На расстояниях от краев рабочего зазора действуют дополнительные магнитные поля (краевые эффекты), что учитывается при расчетах силовых эффектов на ферромагнитовязкий диск, на фиг.10 неоднородность магнитного поля в промежутках δх указана в виде наклонных прямых (хотя распределение в этих промежутках на самом деле нелинейно).

На фиг.11 показано статическое распределение магнитной восприимчивости кромки диска по окружности статора двигателя (фиг.9), когда диск неподвижен. При этом совершенно ясно, что действующие на диск силы взаимно уравновешивают друг друга и никакого самодвижения диска с неподвижного состояния быть не может.

Для анализа действующих на кромку диска тангенциальных сил (втягивающих и тормозящих) при взаимодействии ферромагнитовязкого диска с полюсной парой длиной L (фиг.12) следует иметь в виду, что в центре притяжения полюсной пары (х=0) отсутствует силовое действие на элемент ферромагнетика с мгновенной координатой х=0 и увеличивается к краям зазора, что указано на фиг.13 с учетом краевых эффектов. Поэтому равнодействующая тангенциальная сила ΔF_Σ определяется интегрированием произведений χ(х) G(x), где функция G(x) изменяется в пределах +1≥G(x)≥-1, как указано на фиг.13. Поэтому сила ΔF_Σ пропорциональна выражению:

где s - сечение кромки ферромагнитного диска в магнитном зазоре (при этом dV=s dx).

Из выражения (4) следует, что оптимизация энергетической характеристики ферромагнитовязкого двигателя требует учета краевых эффектов на отрезках δх и достигается при уменьшении напряженности магнитного поля в интервале х≥L/2 до величины Н_min. Последнее обеспечивается в структуре трехкомпонентного статора, развертка которого показана на фиг.14. При выходе ферромагнитовязкого вещества из рабочего зазора оно попадает в магнитное поле с минимальной напряженностью H_min, поэтому магнитная восприимчивость во времени растет медленно, как указано на фиг.15, затем плавно возрастает до величины Н*, оставаясь постоянной вплоть до входа в следующий по ходу вращения диска рабочий зазор.

Одной из возможных модификаций трехкомпонентного статора (фиг.14) может быть выполнение профиля магнитных полюсов последнего по схеме, указанной на фиг.16. Это позволяет сгладить переходы в распределении магнитной восприимчивости, как это видно из фиг.17, и дополнительно увеличить энергетику устройства. Поскольку магнитное поле в таком экспоненциальном зазоре является неоднородным, то центр магнитного тяготения в рабочей зоне насыщающего магнитного поля длиной L находится в линейном приближении распределения напряженности магнитного поля на длине L из формулы где α=Н_max/Н_min*, Н_min* - напряженность магнитного поля в начале зоны насыщения длиной L. Из этой формулы видно, что при однородном магнитном поле, то есть при α=1, получаем для положения центра магнитного притяжения Х_о=0,5 L, где значение Х_о отсчитывается от начала рабочего магнитного зазора длиной L. Расчет силовых характеристик при неоднородном магнитном поле в рабочем зазоре производится аналогично ранее указанному с учетом смещения центра магнитного тяготения от положения L/2 на величину Х_о - L/2 к концу рабочего зазора.

Вращательный момент ферромагнитовязкого диска М_вращ определяется произведением тангенциальной силы ΔF_Σ на активный радиус диска R и число полюсных пар n в двигателе, а мощность двигателя определяется произведением момента М_вращ на угловую скорость ω вращения диска:

На фиг.18 представлена кривая М_вращ с максимумом на частоте ω_о, значение которой с учетом функции веса G(x) равно:

То обстоятельство, что мощность двигателя согласно (5) характеризуется немонотонной функцией, объясняется просто: при малой частоте ω очень быстро происходит установление магнитной восприимчивости в начальной зоне рабочего зазора, а