Способ определения безразмерного параметра развития трещины

Способ определения безразмерного параметра развития трещины

Иллюстрации

Показать все

Реферат

Изобретение относится к неразрушающим методам контроля и может быть использовано для определения длительной прочности хрупких материалов, в которых скорость развития трещины описывается [Эванс А.Г., Ленгдон Т.К. Конструкционная керамика. - М.: Металлургия, 1980. - 256 c., c115] уравнением

где - стартовая скорость трещины при значении коэффициента интенсивности напряжений (КИН) , n - безразмерный параметр, при неубывающем во времени напряжении σ; этот же параметр при циклическом нагружении будем обозначать m. Для одного и того же материала значение n (или m) зависит от типа развивающейся трещины (отрыва - I, продольного или поперечного сдвига II, III). Интегрирование (1) позволяет [Эванс А.Г., Ленгдон Т.К. Конструкционная керамика. - М.: Металлургия, 1980. - 256 с., с.117] определить долговечность τ изделия, например, при заданном напряжении σ, а следовательно, и отношение долговечностей τ₁ и τ₂ при неизменных напряжениях σ₁ и σ₂ и прочих равных условиях:

Знание безразмерного параметра n (или m) позволяет прогнозировать большие долговечности (при низких напряжениях σ) по результатам кратковременных испытаний (τ=100 с) при высоких напряжениях. Этим и обусловлена актуальность определения безразмерного параметра для конкретного материала.

Известны оперативные способы определения n (или m) на образцах с искусственными трещинами [Эванс А.Г., Ленгдон Т.К. Конструкционная керамика. - М.: Металлургия, 1980. - 256 с., с.104-108], заключающиеся в нагружении образцов, регистрации изменения во времени нагрузки или длины трещины и в расчете по результатам эксперимента значения n на основании (1). Недостаток этих методов заключается в том, что неизвестен тип трещины, развивающейся при длительном нагружении в реальном изделии. В частности, существовало мнение, что в хрупких материалах развиваются трещины отрыва, и для прогнозирования долговечности определяли n для трещин отрыва. При сопоставлении [Завада В.П., Никольский С.Г., Стрижало В.А., Тереньтьев В.П. Сопротивляемость разрушению феррита в условиях длительного нагружения // Пробл. прочности. - 1988. - №8. С.42-46] значений n, полученных из (1) и из (2), оказалось, что реально значение n в 2 раза меньше, чем n, полученные для искусственных трещин в условиях отрыва. Недавно показано [Никольский С.Г. Анализ изломов керамических стержней при кратковременном и длительном изгибе // Пробл. прочности. - 2002. - №5. С.133-143], что катастрофическое разрушение хрупких материалов подготавливается в основном развитием трещин сдвига.

Наиболее близок к предлагаемому изобретению способ определения безразмерного параметра развития трещины [Взаимосвязь распределений прочностных показателей керамических элементов при различных режимах нагружения. / В.А.Медведь, С.Г.Никольский, Л.А.Пупшис, В.П.Терентьев // Электрон. техника. Сер.8. Управление качеством и стандартизация. - 1979. - Вып.6. - С.20-30, Завада В.П., Никольский С.Г., Стрижало В.А., Тереньтьев В.П. Сопротивляемость разрушению феррита в условиях длительного нагружения // Пробл. прочности. - 1988. - №8. С.42-46], включающий:

- комплектацию 2...5 представительных выборок, в каждой из которых количество образцов q>150 [Взаимосвязь распределений прочностных показателей керамических элементов при различных режимах нагружения. / В.А.Медведь, С.Г.Никольский, Л.А.Пупшис, В.П.Терентьев // Электрон. техника. Сер.8. Управление качеством и стандартизация. - 1979. - Вып.6. - С.20-30];

- нагружение образцов различными по значению, но постоянными во времени нагрузками L₁...L_i...L₅, воспроизводящими напряженное состояние материала при эксплуатации изделия [Взаимосвязь распределений прочностных показателей керамических элементов при различных режимах нагружения. / В.А.Медведь, С.Г.Никольский, Л.А.Пупшис, В.П.Терентьев // Электрон. техника. Сер.8. Управление качеством и стандартизация. - 1979. - Вып.6. - С.20-30];

- регистрацию при каждом напряжении σ_i, рассчитываемом по L_i, долговечностей τ_i1, τ_i2, ...τ_ij, ...τ_ik; k_m<q, т.к. часть образцов не разрушается, что мешает определить выборочное среднее и оценить по нему соответствующее математическое ожидание [Взаимосвязь распределений прочностных показателей керамических элементов при различных режимах нагружения. / В.А.Медведь, С.Г.Никольский, Л.А.Пупшис, В.П.Терентьев // Электрон. техника. Сер.8. Управление качеством и стандартизация. - 1979. - Вып.6. - С.20-30];

- определение статистической обработкой [Завада В.П., Никольский С.Г., Стрижало В.А., Тереньтьев В.П. Сопротивляемость разрушению феррита в условиях длительного нагружения // Пробл. прочности. - 1988. - №8. С.42-46] полученных результатов отношений τ_1j/τ_ij при σ=σ₁, и σ=σ_i, нахождение определенного значения безразмерного параметра n по уравнению (2).

Недостаток прототипа - трудоемкость и длительность статистического эксперимента.

Предлагаемое изобретение сокращает трудоемкость и длительность эксперимента.

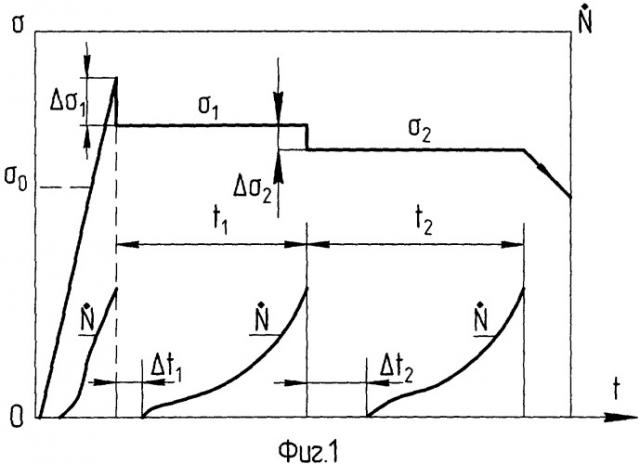
Задачу решают следующим образом. Как и в прототипе, нагружают образцы материала нагрузкой, воспроизводящей напряженное состояние материала при эксплуатации изделия, но в отличие от прототипа предварительно для каждого образца неразрушающим методом (см., например, авт.св. №1620930, МКИ⁵ G01N 29/00, опубл. 15.01.91, Б.И. №2) определяют значение L₀ максимальной неразрушающей нагрузки, а затем, превысив ее, проводят частичные разгрузки (фиг.1), регистрируют активность акустической эмиссии (АЭ), а также интервалы времени до возникновения АЭ после каждой частичной разгрузки (Δt_i) и до восстановления активности АЭ (t_i), а по этим результатам судят о значении безразмерного параметра. Для трещины без сосредоточенной нагрузки на ее поверхности и находящейся в поле номинальных напряжений σ КИН записывают [Механика разрушения и прочность материалов: Справочное пособие в 4 т. / Под общей редакцией В.В.Панасюка. T.1. Основы механики разрушения. - Киев: Наук. думка, 1988. - 488 с.] в виде , где Y - коэффициент, учитывающий соотношение размеров тела и трещины, а также другие ее особенности. Обозначим через ρ размер той зоны перед вершиной трещины (фиг.2), в которой реализуется механизм разрушения микропластическими деформациями, предшествующими образованию новой поверхности; ρ=ρ₀ при θ=0. Если условие микропластичности можно записать через компоненты тензора напряжений и параметр Λ, характеризующий свойства материала, то , где Λ имеет размерность напряжения. При заданном θ , а

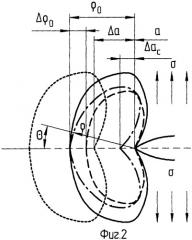
При быстрой разгрузке , а , где Δρ - уменьшение ρ₀ при снижении σ на Δσ. При дальнейшей выдержке при σ=const трещина будет подрастать, увеличивая К, без АЭ - в силу эффекта Кайзера, Когда трещина подрастет таким образом за время Δt на величину Δa_c (фиг.2), граница новой зоны соприкоснется с границей старой. При этом

Дальнейшее подрастание трещины на величину Δа при σ-Δσ будет сопровождаться АЭ и приведет к восстановлению значения ρ₀ (см. короткий пунктир на фиг.2), а следовательно, и К через интервал времени t. В этот момент , и в соответствии с (3)

В период Δt сопротивление материала распространению трещины ниже обычного, так как по крайней мере часть микропластических деформаций перед вершиной трещины произошла до частичной разгрузки, и показатель степени в (1) может отличаться от n - его обозначаем через m. На основании (4) запишем

или в соответствии с (5) -

а с учетом (1) -

Подставив этот результат в (6), после логарифмирования получим

Скорость счета АЭ определяется скоростью роста трещины и размером ρ зоны перед вершиной трещины. Величины и ρ определяются значением КИН. В силу этого восстановление после частичной разгрузки свидетельствует о достижении прежнего значения К при более низкой нагрузке L=const. С учетом этого по аналогии с (7) находим

Фиг.1. Изменение напряжения σ и активности АЭ при определении безразмерного параметра неразрушающим методом: σ - напряжение, - активность АЭ, t - время, Δt_i - интервал времени от момента разгрузки до появления АЭ, t_i - интервал времени до восстановления активности АЭ.

Фиг.2. Границы зоны реализации механизма разрушения у вершины трещины (сплошная линия - перед разгрузкой; длиннопунктирная - после частичной разгрузки; штрихпунктирная - в момент касания исходной границы после подрастания трещины; короткопунктирная - после достижения прежнего значения коэффициента интенсивности напряжения, КИН; (a - длина трещины, Δa - приращение a, Δa_c≈Δρ₀ - возможное перемещение вершины трещины без АЭ при частичной разгрузке; ρ - радиус-вектор точки на границе зоны при произвольном угле θ; ρ₀=ρ при θ=0).

Предложенный способ реализовали изгибом стержней сечением 8×8 мм по четырехточечной схеме (в условиях чистого изгиба) на стандартных устройствах. Выдержку при σ₁ (фиг.1) проводили не менее 100 с. АЭ регистрировали с помощью прибора АФ-15 с уровнем собственных шумов 7 мкВ. Использовали резонансный пьезокерамический преобразователь (в диапазоне частот) 20...200 кГц. Предварительные сравнительные испытания показали, что этот преобразователь фиксирует наибольшее количество импульсов АЭ по сравнению с другими при прочих равных условиях. На образец устанавливали два датчика, каждый с усилием поджатия 2 Н. Для улучшения акустического контакта датчика с поверхностью образца использовали смазку. Параллельно проводили длительные испытания по способу-прототипу. В таблице приведены значения m и n, определенные с учетом тангенса угла наклона кривых длительной прочности в логарифмических координатах. Ввиду разброса экспериментальных точек вокруг аппроксимирующих прямых тангенсы угла наклона, а следовательно, и значения m и n, определены с погрешностью 15...20%. Там же представлены средние m_cp и n_cp значений m и n, полученных по формулам (7) и (8) при обработке результатов испытаний 16-20 стержней каждой керамики, испытанных с регистрацией АЭ (фиг.1).

Результаты кратковременных и длительных испытаний керамических материалов при Т=295±2К
Керамика	m	n	mcp	ncp
Al2O3	8	30	8,0	32
SiC	7	24	6,8	25
Si3N4	16	61	15,0	60
MgF2	9	29	7,9	34
BaTiO3	10	37	11,0	36
Фарфор	10	40	9,9	42
Феррит	10	37	9,5	36
Строительная	10	38	10,0	37

Значения m_cp и n_cp случайно отличались от значений m и n, полученных по результатам длительных испытаний. Коэффициенты вариации значений m и n, рассчитанных по (7) и (8), в среднем составляют 6%, что соответствует погрешности 12% при Р=0,95. При этом доверительный интервал среднего по 20 результатам не превышает 3%. Следовательно, использование АЭ при определении m_cp и n_cp позволяет значительно уменьшить погрешность и трудоемкость по сравнению с оценкой m и n по результатам длительных испытаний. Для выяснения возможного влияния размеров изделий на значения m, n и σ₀ их определяли при комнатной температуре с использованием АЭ в условиях изгиба силой посередине пролета трехметровых панелей из строительной керамики, фарфоровых метровых стержней диаметром 200 мм, а также их фрагментов, вырезанных вдоль оси изделия. На каждом изделии или образце определяли от 9 до 16 значений m, n и σ₀. С этой целью между контрольными нагружениями изделие поворачивали вокруг оси или сдвигали на опорах вдоль оси так, чтобы область приложения силы не перекрывалась с предыдущей по длине образца. Уменьшение объема объекта испытаний приводит к повышению σ₀, но практически не влияет на значения m, n и их разброс.

Предложенный способ позволяет оперативно на изделиях определить значения m и n без изготовления образцов за время в сотни раз меньшее, чем требует для этой задачи прототип.

Способ определения безразмерного параметра развития трещины, включающий нагружение образца различными по значению, но постоянными во времени нагрузками, воспроизводящими напряженные состояния материала образца при эксплуатации изделия, отличающийся тем, что предварительно для образца экспериментально определяют значение максимальной неразрушающей нагрузки, превышают его, а затем проводят частичные разгрузки, регистрируют активность акустической эмиссии, а также интервалы времени до возникновения акустической эмиссии после каждой частичной разгрузки и до восстановления активности акустической эмиссии, и по этим результатам определяют значения безразмерного параметра по выражениям

где n и m - значения безразмерного параметра, σ - напряжение, Δt_i - интервал времени от момента разгрузки до появления АЭ, t_i - интервал времени до восстановления активности АЭ.