Способ формирования хаотической последовательности псевдослучайных сигналов

Способ формирования хаотической последовательности псевдослучайных сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники, в частности к формированию псевдослучайных сигналов, и может быть использовано в радиосистемах со сложньми сигналами.

Известен аналог предложенного способа, заключающийся в том, что псевдослучайная последовательность импульсов формируется путем формирования каждого импульса в момент, когда пилообразный результат интегрирования постоянного напряжения увеличивают до напряжения порога обнуления (А.с. СССР № 733093. Способ формирования псевдослучайной последовательности импульсов и устройство для его осуществления. - МПК₂: Н03К 3/84. - Бюл. № 17, 05.05.80). Недостаток известного аналога состоит в том, что точность регулирования дисперсии интервалов между импульсами зависит от точности формирования пилообразного напряжения.

Также известен аналог предложенного способа, заключающийся в том, что хаотические колебания формируются генератором хаотических колебаний, содержащим резистор, первый и второй выводы которого соединены с первыми выводами соответственно первого и второго конденсаторов (Патент RU № 2246790. Генератор хаотических колебаний. - МПК₇: Н03В 29/00. - Бюл. № 5, 20.02.2005). Недостатком известного аналога является отсутствие воспроизводимости статистических характеристик колебаний, формируемых генератором при переходе от одного образца к другому.

Наиболее близким аналогом является способ формирования хаотической последовательности псевдослучайных сигналов, заключающийся в преобразовании случайной последовательности сигналов посредством численного интегрирования нелинейной системы дифференциальных уравнений с динамическим хаосом в хаотическую последовательность псевдослучайных сигналов с постоянным шагом временного отсчета. (Дмитриев А.C., Панас А.И. Динамический хаос: новые носители информации для систем связи. - М.: Изд-во Физико-математической литературы, 2002. - С.139). Данный аналог принят за прототип.

Недостатком известного способа, принятого за прототип, является относительно большие временные интервалы корреляции формируемых сигналов.

Основной задачей, на решение которой направлено заявляемое изобретение, является сокращение временных интервалов корреляции, влияющих на улучшение корреляционных характеристик формируемых сигналов.

Техническим результатом заявляемого изобретения является улучшение корреляционных характеристик формируемой хаотической последовательности псевдослучайных сигналов.

Указанный технический результат достигается тем, что, в известном способе формирования псевдослучайных сигналов, заключающемся в преобразовании случайной последовательности сигналов посредством численного интегрирования нелинейной системы дифференциальных уравнений с динамическим хаосом в хаотическую последовательность псевдослучайных сигналов, согласно предложенному техническому решению,

хаотическую последовательность псевдослучайных сигналов формируют интегрированием с переменным шагом временного отсчета, прямо пропорциональным глубине модуляции и временной функции управляющего воздействия, определяемым по формуле:

,

где t_i - шаг временного отсчета,

i - порядковый номер шага,

Δt - постоянная шага,

m - глубина модуляции колебаний,

f_i - временная функция управляющего воздействия, например, f_i=sgn(X_i), где X_i - величина сигнала;

глубину модуляции берут в пределах m∈(0,М], где М>1.

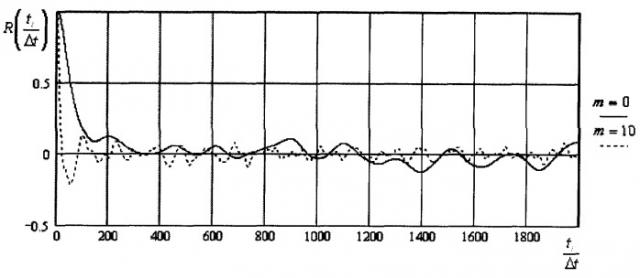
На чертеже показаны графики корреляционных функций сигнала Х_i системы Лоренца.

Сущность предложенного способа формирования псевдослучайных сигналов заключается в следующем.

Изначально сформированную случайную последовательность сигналов преобразуют в хаотическую последовательность псевдослучайных сигналов посредством численного интегрирования нелинейной системы дифференциальных уравнений с динамическим хаосом, например системы Лоренца,

X_i+1=X_i+t_i(-σX_i+σY_i),

Y_i+1=Y_i+t_i(rX_i-Y_i-X_iZ_i),

Z_i+1=Z_i+t_i(-bZ_i+X_iY_i),

с переменным шагом временного отсчета, прямо пропорциональным глубине модуляции и временной функции управляющего воздействия, определяемым по формуле:

t_i=Δt(1+mf_i-1),

где Х_i, Y_i, Z_i - псевдослучайные сигналы;

i - порядковый номер шага;

Δt - постоянная шага;

m - глубина модуляции воздействия, m∈ (0,М], где М>1;

t_i - шаг временного отсчета;

f_i-1 - временная функция управляющего воздействия, где

X*, Y*, Z* - координаты точек равновесия системы;

а - постоянная величина, равная 0.1, 0.5, 0.8;

X*=Y*=, Z*=r-1.

Пример осуществления предложенного способа формирования хаотической последовательности псевдослучайных сигналов.

Изначально сформированную случайную последовательность сигналов Х₀=8.86, Y₀=8.97 и Z₀=27 преобразовывали посредством численного интегрирования системы Лоренца с параметрами уравнений σ=10, r=28 и b=8/3 с переменным шагом временного отсчета t_i, определяемым по формуле

t_i=Δt(1+mf_i-1), где Δt=0.01, m∈(0,10].

Результаты оценки корреляционных функций R(t_i/Δt) хаотических сигналов показаны на приведенной фигуре, где сплошная линия - при m=10, штриховая линия - при m=0.

В результате использования предложенного способа получено значительное сокращение временных интервалов корреляции хаотической последовательности сигналов, приведенных в таблице.

Таблица.Пределы изменений временных интервалов корреляции
А	m
0.1	2	0.82...0.9	0.83...0.9	0.79...0.92	0.82...1.15	0.28...2.02
	5	0.73...0.75	0.72...0.75	0.72...0.74	0.58...0.73	0.2...0.82
	10	0.57...0.61	0.58...0.61	0.55...0.62	0.43...0.57	0.18...0.5
0.5	2	0.64...0.75	0.64...0.72	0.63...0.69	0.56...0.77	0.21...0.87
	5	0.43...0.46	0.43...0.47	0.4...0.45	0.33...0.43	0.12...0.43
	10	0.28...0.33	0.32...0.34	0.3...0.33	0.27...0.31	0.08...0.28
0.8	2	0.53...0.58	0.52...0.57	0.48...0.57	0.41...0.58	0.18...0.6
	5	0.28...0.31	0.28...0.29	0.25...0.3	0.21...0.28	0.08...0.25
	10	0.13...0.15	0.15...0.16	0.14...0.15	0.15...0.17	0.05...0.18

Где , , , , - значения корреляции по уровням 0.8, 0.6, 0.4, 0.2, 0.0 относительно максимального значения корреляционных функций τ₀ без внешнего воздействия.

1. Способ формирования хаотической последовательности псевдослучайных сигналов, заключающийся в преобразовании случайной последовательности сигналов посредством численного интегрирования нелинейной системы дифференциальных уравнений с динамическим хаосом в хаотическую последовательность псевдослучайных сигналов, отличающийся тем, что хаотическую последовательность псевдослучайных сигналов формируют интегрированием с переменным шагом временного отсчета, прямо пропорциональным глубине модуляции и временной функции управляющего воздействия, определяемым по формуле:

t_i=Δt(l+mf_i-1);

где t_i - шаг временного отсчета;

i - порядковый номер шага;

Δt - постоянная шага;

m - глубина модуляции колебаний;

f_i - временная функция управляющего воздействия, например, f_i=sgn(X_i),

где X_i - величина сигнала.

2. Способ по п.1, отличающийся тем, что глубину модуляции берут в пределах m∈(0,М], где М>1.