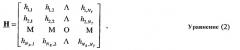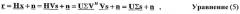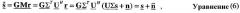Получение собственных векторов для пространственной обработки в системах связи mimo

Получение собственных векторов для пространственной обработки в системах связи mimo

Иллюстрации

Показать все

Реферат

2420-132239RU/091

Область техники, к которой относится изобретение

Настоящее изобретение относится в общем случае к передаче данных, а более конкретно к методикам получения собственных векторов на основе управляющего опорного сигнала, которые используются для пространственной обработки в системе связи множественного ввода/вывода (MIMO).

Уровень техники

Система MIMO использует множество (N_Т) передающих антенн и множество (N_R) приемных антенн для передачи данных. Канал MIMO, сформированный с помощью N_T передающих и N_R приемных антенн, может разбиваться на N_S независимых или пространственных каналов, где N_S≤min{N_T, N_R}. Каждый из N_S независимых каналов соответствует измерению. Система MIMO может обеспечивать улучшенную производительность (например, увеличенную пропускную способность и/или большую надежность), если дополнительные измерения, созданные с помощью множества передающих и приемных антенн эффективно используются.

В системе радиосвязи данные, которые будут передаваться, обычно обрабатываются (например, кодируются и модулируются) и затем преобразуют с повышением частоты к радиочастоте (РЧ) несущего сигнала для генерации модулированного сигнала РЧ, который больше подходит для передачи по беспроводному каналу. Для беспроводной системы MIMO до N_T модулированных сигналов РЧ может генерироваться и передаваться одновременно от N_T передающих антенн. Переданные модулированные сигналы РЧ могут достигать N_R приемных антенн через множество путей распространения в беспроводном канале. Характеристики путей распространения обычно изменяются во времени из-за различных факторов, таких как, например, затухания, многолучевое распространение и внешние помехи. Следовательно, модулированные РЧ сигналы могут находиться в каналах с различными условиями (например, с различным затуханием и с различным влиянием многолучевого распространения) и могут быть связаны с различными сложными коэффициентами усиления и отношениями сигнал-шум (ОСШ, SNR).

Для достижения высокого качества часто необходимо оценивать ответ (характеристику) беспроводного канала связи между передатчиком и приемником. Для системы MIMO ответ канала может характеризоваться с помощью матрицы H ответа канала, которая включает в себя N_TN_R значений сложного коэффициента усиления для N_TN_R различных пар передающая/приемная антенна (т.е. один сложный коэффициент усиления для каждой из N_T передающих антенн и для каждой из N_R приемных антенн). Оценку канала обычно выполняют с помощью передачи пилот-сигнала (т.е. опорного сигнала) с передатчика на приемник. Пилот-сигнал обычно генерируют на основе известных пилотных символов и обрабатывают известным способом (т.е. известным приемнику априорно). Приемник может затем оценивать коэффициенты усиления каналов как отношение принятых пилотных символов к известным пилотным символам.

Оценка ответа канала может быть необходима передатчику для выполнения пространственной обработки для передачи данных. Оценка ответа канала может также быть необходима приемнику для выполнения пространственной обработки (или согласованной фильтрации) принятых сигналов для восстановления переданных данных. Пространственная обработка должна выполняться приемником и обычно также выполняется передатчиком для использования N_S независимых каналов канала MIMO.

Для системы MIMO относительно большое количество системных ресурсов может быть необходимо для передачи пилот-сигнала от N_T передающих антенн, так что достаточно точная оценка ответа канала может быть получена приемником в присутствии шума и помех. Кроме того, большие вычисления обычно необходимы для обработки коэффициентов усиления канала для получения собственных векторов, необходимых для пространственной обработки. В частности, приемник обычно должен обрабатывать коэффициенты усиления каналов для получения первого набора собственных векторов, используемых для пространственной обработки для приема данных в одной линии связи, и может дополнительно получать второй набор собственных векторов, используемых для пространственной обработки для передачи данных в другой линии связи. Получение собственных векторов и пространственная обработка для передачи и приема данных описана ниже. Второй набор собственных векторов обычно необходимо посылать назад передатчику для его использования. Как можно заметить, большое количество ресурсов может быть необходимо для поддержания пространственной обработки в передатчике и приемнике.

Поэтому в уровне техники существует потребность в более эффективной методике получения собственных векторов, используемых для пространственной обработки в системах MIMO.

Сущность изобретения

Представлены методики получения собственных векторов на основе управляющего опорного сигнала, которые используются для пространственной обработки для приема и передачи данных. Управляющий опорный сигнал является пилот-сигналом, передаваемым только в одном пространственном канале или в собственной моде канала MIMO в течение заданного периода символа, что достигается с помощью выполнения пространственной обработки с помощью управляющего вектора для этой собственной моды, как описано ниже. Управляющий опорный сигнал используется приемником для получения оценки и диагональной матрицы Σ сингулярных значений и унитарной матрицы U левых собственных векторов матрицы H ответа канала, без необходимости оценки ответа канала MIMO или выполнения разложения по сингулярным числам матрицы H.

Оценки Σ и U могут использоваться для согласованной фильтрации передачи данных, принятой через первую линию связи (например, восходящую линию связи). Для системы дуплексной связи с временным разделением каналов (ДСВРК, TDD), которая характеризуется ответами канала нисходящей линии связи и восходящей линии связи, которые являются обратной величиной друг друга, оценка U может также использоваться для пространственной обработки передачи данных во второй линии связи (например, в нисходящей линии связи).

В другом аспекте матрицу с ортогональными столбцами получают на основе оценок Σ и U. Ортогонализация столбцов может достигаться с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция, которые все описаны ниже. Ортогональная матрица согласованного фильтра может затем быть получена на основе матрицы и оценки Σ. Матрица может использоваться для согласованной фильтрации для первой линии связи, и матрица может использоваться для пространственной обработки для второй линии связи.

Различные аспекты и варианты осуществления изобретения описаны более подробно ниже.

Краткое описание чертежей

Признаки, характер и преимущества настоящего изобретения станут более очевидными из сформулированного ниже подробного описания, которое рассматривают вместе с чертежами, на которых одинаковые обозначения идентифицируют соответственные элементы по всему документу и на которых:

фиг.1 показывает последовательность операций процесса получения ортогональной матрицы согласованного фильтра на основе управляющего опорного сигнала;

фиг.2 показывает систему радиосвязи;

фиг.3 показывает структуру кадра для системы ДСВРК MIMO-OFDM;

фиг.4 показывает передачу управляющего опорного сигнала и данных в нисходящей линии связи и восходящей линии связи для примерной схемы передачи;

фиг.5 показывает структурную схему точки доступа и пользовательского терминала; и

фиг.6 показывает структурную схему пространственной обработки, выполняемой с помощью точки доступа и пользовательского терминала для передачи данных в нисходящей линии связи и восходящей линии связи.

Подробное описание

Используемое в данной работе слово "примерный" означает "служить примером или иллюстрацией". Любой вариант осуществления или образец, описанный как "примерный", не обязательно должен рассматриваться как предпочтительный или преимущественный по сравнению с другими вариантами осуществления или образцами.

Описанные методики для получения собственных векторов могут использоваться для различных систем связи MIMO. Например, эти методики могут использоваться для систем MIMO с одной несущей, а также для систем MIMO с многими несущими. Для ясности эти методики описаны ниже для системы MIMO с одной несущей.

Модель для системы MIMO с одной несущей может быть выражена как:

Где x - "передаваемый" вектор с N_T элементами для символов, посланных от N_T передающих антенн (т.е. x=[x₁ x₂ ... x_Nт]^T);

R - "принимаемый" вектор с N_R элементами для символов, принятых через N_R приемных антенн (т.е. r=[r₁ r₂ ... r_NR]^T);

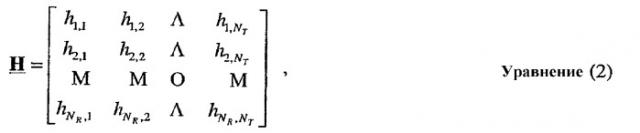
H - матрица ответа канала (N_R × N_T);

n - вектор аддитивного белого Гауссова шума (AWGN); и

"^T" обозначает транспозицию.

Вектор шума n, как предполагают, имеет компоненты с нулевым значением и ковариационной матрицей , где I - единичная матрица, и - шумовая дисперсия.

Матрица H ответа канала может быть выражена как:

где элемент h_i,j, для i ∈ {1... N_R} и j ∈ {1... N_T}, является связью (т.е. сложным коэффициентом усиления) между j-й передающей антенной и i-й приемной антенной. Для простоты ответ канала, как предполагают, является плоским по всей ширине полосы пропускания системы, и ответ канала для каждой пары антенн передачи/приема может быть представлен единственным сложным значением h_i,j. Также для простоты последующее описание предполагает, что N_R ≥ N_T, матрица H ответа канала имеет полный ранг и N_S=N_T ≤ N_R.

Матрица H ответа канала может "диагонализироваться" для получения N_T независимых каналов, которые также упоминаются как пространственные каналы или собственные моды. Эту диагонализацию могут достигать с помощью выполнения или разложения по сингулярным числам матрицы H ответа канала или разложения по собственным значениям корреляционной матрицы H, которая является H^HH, где "^H" обозначает сопряженную транспозицию. Для ясности в последующем описании используется разложение по сингулярным числам.

Разложение по сингулярным числам матрицы H ответа канала может быть выражено как:

где U - унитарная матрица (N_R × N_R), столбцами которой являются собственные векторы H;

Σ - диагональная матрица (N_R × N_T) сингулярных значений H, которая определяется как

и

V - унитарная матрица (N_T × N_T), столбцы которой - правые собственные векторы H.

Унитарная матрица М характеризуется свойством M^HM=I, которое означает, что столбцы унитарной матрицы ортогональны друг другу и строки матрицы также ортогональны друг другу. Столбцы матрицы V также упоминаются как управляющие векторы. Разложение по сингулярным числам описано более подробно Гильбертом Странгом (Gilbert Strang) в книге, озаглавленной "Linear Algebra and Its Applications", второе издание, Academic Press, 1980.

Пространственная обработка может выполняться и передатчиком, и приемником для передачи данных в N_T пространственных каналах канала MIMO. Пространственная обработка в передатчике может быть выражена как:

где s - вектор "данных" с количеством ненулевых элементов до N_T для символов данных, которые будут передаваться в N_T пространственных каналах. Передаваемый вектор x дополнительно обрабатывают и затем передают по каналу MIMO на приемник.

Принятая передача в приемнике может быть выражена как:

где все термины определены выше.

Пространственная обработка в приемнике для восстановления вектора данных s может быть выражена как:

где s - вектор данных;

- оценка вектора данных s;

М - (N_T × N_R) матрица согласованного фильтра, которая определяется как M=Σ^TU^H;

G - (N_T × N_T) масштабируемая матрица, которая определяется как

и

- постобработанный шум, который определяется как =GΣ^TU^Hn.

Пространственная обработка с помощью приемника часто упоминается как согласованная фильтрация. Поскольку M=Σ^TU^H и поскольку столбцы U являются собственными векторами H, столбцы М^T являются сопряженными левыми собственными векторами H, масштабированными с помощью сингулярных значений в Σ.

Как показано в уравнении (6), приемнику нужны хорошие оценки матриц Σ и U для выполнения согласованной фильтрации для восстановления вектора данных s. Матрицы Σ и U могут быть получены с помощью передачи пилот-сигнала с передатчика на приемник. Приемник может затем оценивать матрицу H ответа канала, основываясь на принятом пилот-сигнале, и выполнять разложение этой оценки по сингулярным числам, как показано в уравнении (3), для получения матриц Σ и U. Однако, как отмечено выше, большое количество ресурсов может быть необходимо для передачи этого пилот-сигнала и выполнения разложения по сингулярным числам.

I. Управляющий опорный сигнал

В одном из аспектов, управляющий опорный сигнал передают с помощью передатчика и используют приемником для получения оценки матриц Σ и U, которые необходимы для согласованной фильтрации. Управляющий опорный сигнал - передача пилот-сигнала только в одном пространственном канале или собственной моде в течение заданного периода символа, что достигается с помощью выполнения пространственной обработки с помощью управляющего вектора для этой собственной моды. Приемник может затем оценивать матрицы Σ и U, основываясь на управляющем опорном сигнале, без необходимости оценивать ответ канала MIMO или выполнения разложения по сингулярным числам.

Управляющий опорный сигнал, посланный передатчиком, может быть выражен как:

где x_sr,m является переданным вектором для управляющего опорного сигнала для m-й собственной моды; v_m - правый собственный вектор H для m-й собственной моды; и p - пилотный символ, переданный для управляющего опорного сигнала. Собственный вектор v_m является m-м столбцом матрицы V, где V=[v₁v₂ ... v].

Принятый управляющий опорный сигнал в приемнике может быть выражен как:

где r_sr,m является принимаемым вектором для управляющего опорного сигнала для m-й собственной моды; и σ_m - сингулярное значение для m-й собственной моды.

Как показано в уравнении (8), в приемнике принятый управляющий опорный сигнал в отсутствие шума равен u_mσ_mp, что является известным пилотным символом p, преобразованным с помощью u_mσ_m. Собственный вектор u_m является m-м столбцом матрицы U, и сингулярное значение σ_m является m-м диагональным элементом матрицы Σ. Приемник может, таким образом, получать оценку u_mσ_m, основываясь на управляющем опорном сигнале, посланном передатчиком.

Различные методики могут использоваться для обработки принятого управляющего опорного сигнала для получения оценки u_m и σ_m. В одном из вариантов осуществления для получения оценки u_mσ_m принимаемый вектор r_sr,m для управляющего опорного сигнала, посланного на m-й собственной моде, сначала умножают на комплексное сопряжение пилотного символа p*. Результат может затем интегрироваться по многочисленным символам управляющего опорного сигнала, принятым для каждой собственной моды m для получения оценки u_mσ_m. Вектор строки может определяться так, чтобы он был равен сопряженной транспозиции оценки u_mσ_m (т.е. Каждый из N_R элементов вектора получают, основываясь на соответствующем одном из N_R элементов вектора r_sr,m.

Вектор строки для m-й собственной моды включает в себя оценки и u_m, и σ_m и может таким образом упоминаться как масштабируемый вектор. Так как собственные векторы имеют единичную мощность, сингулярное значение σ_m может оцениваться, основываясь на принятой мощности управляющего опорного сигнала, который может измеряться для каждой собственной моды. В частности, оценка сингулярных значений может быть установлена равной квадратному корню мощности для вектора r_sr,m, разделенному на величину пилотного символа p. Вектор может масштабироваться с помощью для получения собственного вектора

В другом варианте осуществления методика минимальной среднеквадратической ошибки (MMSE) используется для получения оценки u_m, основываясь на принимаемом векторе r_sr,m для управляющего опорного сигнала. Поскольку пилотный символ p известен, приемник может получать оценку u_m так, что среднеквадратическая ошибка между восстановленным пилотным символом (который получают после выполнения согласованной фильтрации принимаемого вектора r_sr,m) и переданным пилотным символом p минимизирована.

Управляющий опорный сигнал передают для одной собственной моды каждый момент времени (т.е. одна собственная мода в течение каждого периода символа передачи управляющего опорного сигнала). Управляющий опорный сигнал для всех N_T собственных мод может передаваться различными способами. В одном из вариантов осуществления управляющий опорный сигнал передают для одной собственной моды в течение каждого кадра, где кадр - интервал передачи данных для системы, и его определяют так, чтобы он имел определенную продолжительность времени (например, 2 мс). Для данного варианта осуществления управляющий опорный сигнал для многочисленных собственных мод может передаваться в множестве кадров. В другом варианте осуществления управляющий опорный сигнал передают для многочисленных собственных мод в пределах одного кадра. Это может достигаться с помощью циклического повторения N_T собственных мод в N_T периодах символа. Для обоих вариантов осуществления n-й символ управляющего опорного сигнала может выражаться как:

где n - индекс или для периода символа, или для номера кадра, и L - количество символов управляющего опорного сигнала, которые будут передаваться. Многочисленные символы управляющего опорного сигнала могут передаваться для каждой собственной моды m для предоставления возможности приемнику получать более точную оценку u_mσ_m.

Приемник может получать вектор строки для каждой из N_T собственных мод, основываясь на принятом управляющем опорном сигнале для этой собственной моды. Вектор строки для всех N_T собственных мод может использоваться для формирования начальной матрицы согласованного фильтра где и Матрица может использоваться для согласованной фильтрации приемником, как показано в уравнении (6), для восстановления переданного вектора данных s.

Управляющий опорный сигнал посылают для одной собственной моды каждый момент времени, и он может использоваться приемником для получения вектора согласованного фильтра для этой собственной моды. Поскольку N_T векторов согласованного фильтра матрицы получают индивидуально и за различные периоды символа и из-за шума и других источников ухудшения параметров беспроводного канала, N_T векторов матрицы вряд ли будут ортогональны друг другу. Если N_T векторов после этого будут использоваться для согласованной фильтрации принятой передачи данных, то любые ошибки в ортогональности между этими векторами приведут к перекрестным помехам (взаимному влиянию) между отдельными потоками символов, посланными на N_T собственных модах. Перекрестные помехи могут ухудшать производительность.

II. Ортогонализация собственных векторов

В другом аспекте для улучшения производительности усовершенствованную матрицу согласованного фильтра получают, основываясь на управляющем опорном сигнале, и она имеет векторы строки, которые должны быть ортогональными один относительно другого. Ортогонализацию векторов строк могут выполнять с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция. Все эти методики ортогонализации описаны подробно ниже. Другие методики ортогонализации могут также использоваться, и они находятся в пределах сущности изобретения.

1. QR-разложение

QR-разложение разлагает транспонированную начальную матрицу согласованного фильтра на ортогональную матрицу Q_F и на верхнюю треугольную матрицу R_F. Матрица Q_F формирует ортогональное основание для столбцов матрицы (т.е. строки и диагональные элементы матрицы R_F задают длину компонентов столбцов в направлениях соответствующих столбцов Q_F. Матрицы Q_F и R_F могут использоваться для получения усовершенствованной матрицы согласованного фильтра

QR-разложение может выполняться различными способами, которые включают в себя процедуру Грама-Шмидта (Gram-Schmidt), преобразование Хаусхолдера (Householder) и т.д. Процедура Грама-Шмидта рекурсивна и может быть в цифровой форме нестабильной. Изобретены различные варианты процедуры Грама-Шмидта, и они известны из предшествующего уровня техники. "Классическая" процедура Грама-Шмидта для ортогонализации матрицы описана ниже.

Для QR-разложения матрица может быть выражена как:

где Q_F - ортогональная матрица (N_R × N_R); и R_F - верхняя треугольная матрица (N_R × N_T) с нулями ниже диагонали и возможными ненулевыми значениями по и выше диагонали.

Процедура Грама-Шмидта генерирует матрицы Q_F и R_F столбец за столбцом. Следующие обозначения используются для приведенного ниже описания:

Q_F=[q₁q₂ ... q_N], где q_j является j-м столбцом Q_F;

q_i,j - элемент в i-й строке и j-м столбце Q_F;

где является j-м столбцом

r_i,j- элемент в i-й строке и j-м столбце R_F;

где является j-м столбцом и

является элементом в i-й строке и j-м столбце

Первый столбец Q_F и R_F может быть получен как:

Первый столбец R_F включает в себя одно ненулевое значение r_1,1 для первой строки и нули в других местах, где r_1,1 - вторая норма Первый столбец Q_F является нормализованной версией первого столбца причем нормализацию выполняют с помощью масштабирования каждого элемента с помощью инвертирования r_1,1.

Каждый из оставшихся столбцов Q_F и R_F может быть получен следующим образом:

для j=2, 3, ... N_T

для i=1, 2, ... j-1

Процедура Грама-Шмидта генерирует один столбец за один раз для матрицы Q_F. Каждый новый столбец Q_F должен быть ортогонален ко всем ранее сгенерированным столбцам слева от нового столбца. Это достигают с помощью уравнений (14) и (16), где j-й столбец Q_F (или q_j) генерируют, основываясь на который в свою очередь генерируют, основываясь на j-м столбце (или и вычитая любые компоненты в направленные в направлении других (j-1) столбцов слева от Диагональные элементы R_F вычисляют как вторые нормы столбцов (где как показано в уравнении (15).

Улучшенная производительность может достигаться с помощью упорядочивания матрицы основываясь на оценках сингулярных значений перед выполнением QR-разложения. Начальные оценки сингулярных значений для m ∈ {1 ... N_T} для диагональной матрицы можно вычислять как вторые нормы столбцов как описано ниже. Начальные оценки сингулярных значений можно затем упорядочить так, что где является наибольшей оценкой сингулярных значений и является наименьшей оценкой сингулярных значений. Когда начальные оценки сингулярных значений для диагональной матрицы упорядочиваются, столбцы матрицы также упорядочиваются соответственно. Первый или крайний левый столбец затем связывают с наибольшей оценкой сингулярных значения и самым высоким принятым ОСШ и последний или крайний справа столбец связывают с наименьшей оценкой сингулярных значений и самым низким принятым ОСШ. Для QR-разложения начальные оценки сингулярных значений могут быть получены как вторые нормы столбцов и использоваться для упорядочивания столбцов Конечные оценки сингулярных значений получают как вторые нормы столбцов как описано выше. Управляющий опорный сигнал может также передаваться по порядку (например, от наибольшей собственной моды до наименьшей собственной моды), так чтобы оценки сингулярных значений эффективно упорядочивались передатчиком.

Если столбцы упорядочиваются на основе уменьшения значений соответствующих им оценок сингулярных значений, то столбцы/собственные векторы Q_F должны быть ортогональны к первому столбцу/собственному вектору с лучшим принятым ОСШ. Это упорядочивание таким образом имеет благоприятное воздействие удаления определенных шумовых компонентов каждого из оставшихся собственных векторов Q_F. В частности, j-й столбец Q_F (или q_j) генерируют на основе j-го столбца (или и шумовые компоненты в которые указывают в направлении j-1 собственных векторов слева от q_j (которые связаны с более высокими принятыми ОСШ), вычитают из для получения q_j. Упорядочивание также имеет благоприятное воздействие улучшения оценок собственных векторов, связанных с меньшими сингулярными значениями. Конечным результатом является улучшенная производительность, особенно если ортогонализированные собственные векторы Q_F используются для пространственной обработки для передачи данных в другой линии связи, как описано ниже.

Усовершенствованная ортогональная матрица согласованного фильтра полученная на основе QR-разложения, может затем быть выражена как:

где включает в себя только диагональные элементы R_F (т.е. элементы выше диагонали установлены в нули). Диагональные элементы и R_F - оценки сингулярных значений H. Поскольку M=Σ^TU^H и могут быть сделаны следующие замены: и Q^F=U^*, где "*" обозначает комплексное сопряжение.

2. Вычисление среднеквадратической ошибки и полярная декомпозиция

Начальная матрица согласованного фильтра может также ортогонализироваться на основе определенного критерия оптимальности. Одним из возможных критериев является минимизация величины квадратической ошибки между матрицей и "оптимальным" согласованным фильтром с требуемыми свойствами ортогональности. Это может быть выражено как:

где - норма Фробениуса (Frobenius) для X, и задается как:

Условие гарантирует, что Q_P является унитарной матрицей, что означает, что столбцы Q_P ортогональны друг к другу и строки Q_P также ортогональны друг к другу. Уравнение (18) приводит к оптимальному согласованному фильтру Σ^TQ_P, который наилучшим образом подходит к измеренным данным, представленным с помощью матрицы

Решение уравнения (18) может быть получено из известного решения ортогональной проблемы Прокруста (Procrustes). Эта проблема задает вопрос: если даны две известные матрицы A и В, может ли быть найдена унитарная матрица Q_P, которая превращает В в A. Проблема может быть выражена как:

Решение проблемы Прокруста может быть получено следующим образом. Сначала матрицу C_P определяют как C_P=B^HA. Разложение по сингулярным числам C_P затем представляют как C_P=U_pΣ_P или C_PV_P=Σ_P. Унитарную матрицу Q_P, которая решает проблему минимизации, показанную в уравнении (20), затем представляют как:

Получение и доказательство уравнения (21) описаны G. H. Golub и C. F. Van Loan в "Matrix Computation", Third Edition, Johns Hopkins University Press, 1996.

Решение уравнения (20), которое показано в уравнении (21), относится к полярной декомпозиции матрицы C. Эта полярная декомпозиция задается следующим образом:

где Z_P - унитарная матрица, которая задается как

- матрица левых собственных векторов C_P, которая охватывает место столбца C_P (т.е. равно U_P или субматрице U_P в зависимости от размерности C_P);

P_P - симметрическая положительная полуопределенная Эрмитова (Hermitian) матрица, которая задается как

и

является квадратной матрицей сингулярных значений C_P с размерностью, равной количеству столбцов C_P.

Полярная декомпозиция может таким образом выполняться на матрице C_P для получения унитарной матрицы Z_P, которая может быть равна или Q_P, или субматрице Q_P в зависимости от размерности C_P. Можно показать, что матрица Z_P является оптимальным результатом для проблемы минимизации, показанной в уравнении (20).

Алгоритмы для прямого вычисления полярной декомпозиции описаны P. Zielinski и K. Zietak в "The Polar Decomposition-Properties, Applications and Algorithms," Annals of the Polish Mathematical Society, 38 (1995), и A. A. Dubrulle в "An Optimum Iteration for the Matrix Polar Decomposition," Electronic Transactions on Numerical Analysis, том 8, 1999, стр. 21-25.

Решение для оптимального согласованного фильтра, которое выражено в уравнении (18), может быть получено на основе решения описанной выше ортогональной проблемы Прокруста. Это может выполняться с помощью приравнивания к A и Σ^T к В. Для вычисления оценка сингулярных значений может быть получена как вторая норма столбцов и использоваться вместо Σ. Диагональные элементы могут б