Способ изменения метастабильного состояния вещества

Способ изменения метастабильного состояния вещества

Иллюстрации

Показать все

Реферат

Изобретение относится к области физики конденсированных сред и может быть использовано для изменения физических свойств вещества в диапазоне максимальных тепловых флуктуаций (термофлуктуаций), возникающих при изменении энтальпии вещества в процессе активации теплового распада внутренних связей между частицами, например, при изменении температуры вещества.

Если вещество, находящееся в газообразном или жидком состоянии достаточно охладить, то оно переходит в твердое состояние с относительным постоянством взаимного расположения частиц. Обратная картина конденсации: твердое тело - жидкость - газ - плазма.

При этом наблюдается постоянство массы вещества при всех фазовых переходах и состояниях. Очевидным становится факт, что изменяется лишь энергия взаимодействия, которую вещество обнаруживает в виде отклика на внешнее воздействие.

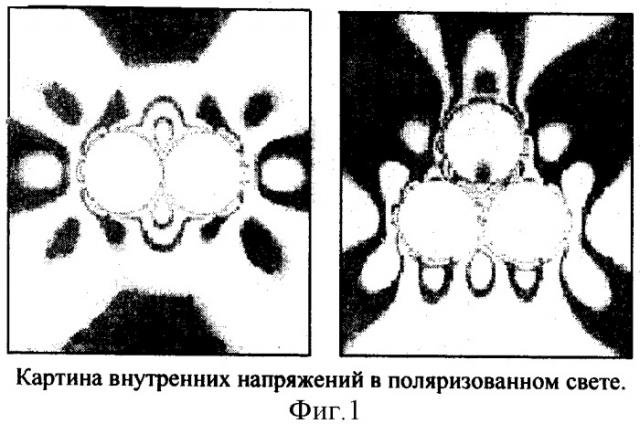
Наглядный пример энергии взаимодействия вещества демонстрирует картина внутренних напряжений в модели из оптически активного материала при поляризационно-оптическом изучении отклика вещества модели на внешнее воздействие (фиг.1).

Вещество в любом фазовом состоянии стремится занять минимальную энергетическую нишу, которую принято называть потенциальной энергией.

Известен фазовый переход первого рода, при котором изменяются структура и свойства вещества, а в точке перехода изменяются скачком плотность и термодинамические функции: энергия, свободная энергия, энтропия, энтальпия и др. К фазовым переходам 1-го рода относятся все агрегатные превращения, переходы одних кристаллических модификаций в другие и т.д. [1].

Известен фазовый переход второго рода, при котором изменяются лишь свойства вещества, без изменения его структуры, при этом плотность и термодинамические функции непрерывны, в силу чего теплота превращения равна нулю. К фазовым переходам 2-го рода относят, например, переход диэлектрик-сегнетоэлектрик с появлением спонтанной поляризации, переходы металлов в сверхпроводящее состояние в отсутствие магнитного поля и др. [2].

Кроме того, физика отмечает фазовый переход, относящийся к упорядочению структуры вещества - так называемая метастабильность свойств. Этот фазовый переход можно наблюдать, например, при получении булата, дамасской стали и др.

Предлагаемым изобретением решается задача определения зоны неравномерного теплового движения частиц, приводящего к тепловым (энергетическим) флуктуациям, и их влияния на долговечность вещества. Она решается при экспериментальном исследовании теплоемкости С_υ вещества: химических элементов, кристалла алмаза и т.д. при температурах от Т=0 К до Т=1300 К с последующими расчетами энтальпии вещества по формуле ΔН=С_υТ. Техническим результатом является определение зоны фазового - метастабильного состояния на кривой энтальпии, расчет времени между максимальными флуктуациями, приводящими к разрыву межатомных связей, скачку внутренней энергии взаимодействия, равной энергии этих флуктуаций.

Технический результат достигается с помощью экспериментального определения значений изменения теплоемкости вещества за счет накачки энергии, повышения/понижения температуры и т.д. с последующим расчетом внутренней энергии вещества - энтальпии, определением окрестности точки разрыва энтальпии - максимальной тепловой флуктуации, расчетом времени между флуктуациями, приводящими к разрыву энтальпии, расчетом энергии максимальной тепловой флуктуации.

Во второй половине ХХ-го столетия исследователи пришли к выводу, что внешняя сила не осуществляет разрыва межатомных связей, а лишь создает условия для их необратимого разрыва тепловыми флуктуациями, т.е. разрушение тел является по своей природе термофлуктуационным процессом [3].

В то же время разрывы связей между частицами вскоре ликвидируются тепловыми флуктуациями за счет реставрации разорванных связей, т.к. флуктуация, необходимая для восстановления связи, не больше флуктуации, вызывающей разрыв связи, а расстояние между частицами находится в пределах энергии флуктуации. Наличие включений или нарушение сплошности вещества: дефектов, трещин, дислокаций и т.д., будут усиливать ход термофлуктуационных разрушений. Следует отметить, что связи между частицами не восстанавливаются, если вещество постоянно испытывает воздействие внешних сил.

Для процесса, протекающего при постоянном давлении, изобарный тепловой эффект (энтальпию) можно найти из суммы функции состояния вещества и работы внешних сил. Следовательно, энтальпия вещества при охлаждении/нагревании в условиях изохорно-изобарного процесса будет равна: ΔН=С_υТ. В свою очередь теплоемкость вещества будет складываться из теплоемкости массы С_m и теплоемкости взаимодействия С_in. Для твердого тела (элемента) С_m=1/2Rlnm, где R - число Авагадро. Теплоемкость взаимодействия можно найти из данных эксперимента, за вычетом постоянной С_m.

Температурные напряжения связаны с долговечностью выражением [4]:

τ=τ_oe^U(σ)/kT,

где τ - среднее время между двумя последовательными флуктуациями;

τ_o˜τ_ч - колебание частицы со средней частотой 10^-13 с:

U(σ)=U_o-γσ=kTln (τ/τ_o) - энергия активации вещества от внутренних температурных напряжений:

k - постоянная Больцмана;

Т - температура;

γ - коэффициент концентрации температурных напряжений;

σ - температурные напряжения.

Итак, функциональная связь величины долговечности с температурой осуществляется в виде «больцмановского» фактора, что позволяет установить конкретную форму, в которой тепловые взаимодействия влияют на долговечность вещества.

В силу хаотичности теплового движения частиц имеют место тепловые энергетические флуктуации. Среднее время τ_фл между двумя одинаковыми флуктуациями с энергией Е_фл описывается равенством U(σ)=Е_фл. Из уравнения

находим

Е_фл=kTln (τ_фл/τ_о),

т.е. получаем энергию активации теплового распада внутренних взаимодействий частиц. Исходя из равенства Е_фл=ΔН=С_inТ, получим среднее время между двумя одинаковыми флуктуациями:

или .

Фазовое состояние вещества при изменении взаимодействия согласно характеру изменения энтальпии (фиг.2-11), т.е. внутренней энергии, необходимо отнести к изменению метастабильного состояния вещества, а зону фазового состояния - к действию термофлуктуаций вещества, приводящих к разрыву кривой энтальпии. Время фазового состояния, т.е. время между двумя флуктуациями τ_фл, вызывающими скачок внутренней энергии вещества, равной энергии флуктуации Е_фл, определяется в окрестности точки разрыва согласно экспериментальной кривой теплоемкости вещества, кривой энтальпии и выше приведенной формулы.

Пример №1.

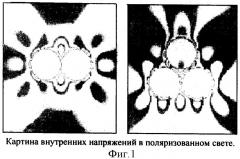
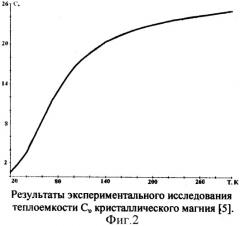
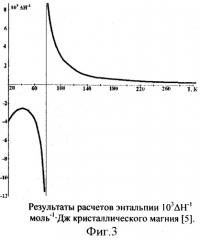
Образцы кристаллического магния, ГПУ(Mg), ₁₂Mg 24,305; С_m=1/2Rln24,305=13,2643 Дж·моль^-1·К^-1 исследовали в диапазоне от 20 К до 300 К. Разделили этот диапазон на экспериментальные точки, измерили значение теплоемкости С_υ, а результаты измерения теплоемкости магния представили на графике (фиг.2). Затем вычислили теплоемкость внутреннего взаимодействия магния С_in=С_υ-С_m и рассчитали значение энтальпии по формуле ΔН=С_inТ. Результаты расчетов энтальпии магния представили на графике (фиг.3), на котором кривые в точке разрыва асимптотически приближаются к прямой.

Пример №2.

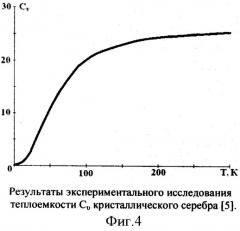
Образцы кристаллического серебра, ГКЦ (Cu), ₄₇Ag 107,8682; С_m=1/2Rln107,8682=19,4595 Дж·моль^-1·К^-1 исследовали в диапазоне от 0 К до 300 К. Разделили этот диапазон на экспериментальные точки, измерили значение теплоемкости С_υ, а результаты измерения теплоемкости серебра представили на графике (фиг.4). Затем вычислили теплоемкость внутреннего взаимодействия серебра С_in=С_υ-C_m и рассчитали значение энтальпии по формуле ΔН=С_inТ. Результаты расчетов энтальпии серебра представили на графике (фиг.5), на котором кривые в точке разрыва асимптотически приближаются к прямой.

Пример №3.

Образцы кристаллического углерода, тетраэдр (алмаз), ₅C 12,011; С_m=1/2Rln12,011=10,3341 Дж·моль^-1·К^-1 исследовали в диапазоне от 0 К до 1300 К. Разделили этот диапазон на экспериментальные точки, измерили значение теплоемкости С_υ, а результаты измерения теплоемкости алмаза представили на графике (фиг.6). Затем вычислили теплоемкость внутреннего взаимодействия алмаза С_in=С_υ-C_m и рассчитали значение энтальпии по формуле ΔН=С_inТ. Результаты расчетов энтальпии алмаза представили на графике (фиг.7), на котором кривые в точке разрыва асимптотически приближаются к прямой.

Пример №4.

Образцы кристаллического соединения XeF₆, m=245,290; С_m=1/2Rln 245,290=22,290 Дж·моль^-1·К^-1 исследовали в диапазоне от 0 К до 100 К. Разделили этот диапазон на экспериментальные точки, измерили значение теплоемкости С_υ, а результаты измерения теплоемкости XeF₆, представили на графике (фиг.8). Затем вычислили теплоемкость внутреннего взаимодействия XeF₆ С_in=С_υ-C_m и рассчитали значение энтальпии по формуле ΔН=С_inТ. Результаты расчетов энтальпии XeF₆ представили на графике (фиг.9), на котором кривые в точке разрыва асимптотически приближаются к прямой.

Пример №5.

Образцы кристаллического NH₄NO₃, m=80,0432; C_m=12Rln80,0432=18,219 Дж·моль^-1·К^-1 исследовали в диапазоне от 0 К до 300 К. Разделили этот диапазон на экспериментальные точки, измерили значение теплоемкости С_υ, а результаты измерения теплоемкости NH₄NO₃ представили на графике (фиг.10). Затем вычислили теплоемкость внутреннего взаимодействия NH₄NO₃ С_in=С_υ-C_m и рассчитали значение энтальпии по формуле ΔН=С_inТ. Результаты расчетов энтальпии NH₄NO₃ представили на графике (фиг.11), на котором кривые в точке разрыва асимптотически приближаются к прямой.

Результаты расчетов энтальпии 10³ ΔН^-1 Дж·моль^-1 по приведенным данным экспериментального исследования теплоемкости химических элементов Mg, Ag, С, соединений XeF₆ и NH₄NO₃, опубликованными в литературе [5-8], показали повторяющуюся закономерность кривых энтальпии с характерным экстремумом левой части графика, зону разрыва от тепловых флуктуаций и понижающуюся кривую правой части графика. Обе кривые асимптотически приближаются к зоне разрыва, определяемой временем между двумя максимальными флуктуациями τ_фл и характеризующейся энергией флуктуации Е_фл, что позволяет судить об изменении метастабильного состояния вещества.

Графики изменения энтальпии химических элементов Mg, Ag, С, соединений XeF₆ и NH₄NO₃ в зависимости от температуры (фиг.2-11) показывают, что внутреннее взаимодействие частиц (компонентов) вещества сопротивляется внешнему воздействию: вначале оно нарастает, достигает максимума, затем снижается, пока не наступает разрыв внутренних связей. Фазовое равновесие без химического взаимодействия между частицами в однокомпонентной системе и компонентов в гетерогенной системе сопровождается процессами перехода частиц (компонентов) из одной фазы в другую. Зона этого фазового равновесия осуществляется действием возникающих и исчезающих тепловых флуктуаций только в этой зоне, что не сопровождается в целом изменением внутренней энергии вещества. Именно эта зона фазового равновесия, в которой тепловые флуктуации разрывают связи взаимодействия частиц (компонентов), а затем восстанавливают их, где происходит резкий скачок энтальпии, является зоной изменения метастабильного состояния вещества.

Использованные источники

1. Физический энциклопедический словарь в 5 т. М.: БСЭ, т.5, 1966, с.575.

2. Химическая энциклопедия в 5 т. М.: БСЭ. т.5, 1988, с.983.

3. С.Н.Журков, Вестник АН СССР, №11, 1957, с 78; №3, 1968, с.46.

4. В.Р.Регель, А.И.Слуцкер, Э.И.Томашевский, УФН, 106, 193, 1972.

5. М.Х.Карапетьянц, Химическая термодинамика. - М.: Химия, 1975, 583 С.

6. Б.H.Бушманов, Ю.А.Хромов, Физика твердого тела. - М.: Высшая школа, 1971, 221 С.

7. Э.А.Мелвин-Хьюз, Физическая химия в 2 кн, пер. с англ. - М.: ИИЛ, 1962, кн. 1, 519 С.

8. Термодинамические свойства индивидуальных веществ. Спр. изд. в 4 т. /Под редакцией В.П.Глушко/ - М.: Наука, 1978, т.1, кн. 2, 327 С.

1. Способ изменения метастабильного состояния вещества за счет активации теплового распада внутренних связей между частицами в диапазоне максимальных термофлуктуаций, возникающих в процессе изменения энтальпии вещества, при этом экспериментально исследуют вещество в диапазоне температур, начиная с Т=0 К, измеряют значения теплоемкости вещества в этом диапазоне и по резкому скачку энтальпии судят о зоне изменения метастабильного состояния вещества.

2. Способ по п.1, отличающийся тем, что при изменении цветности кристаллов, типа алмаза, или аморфных структур, типа стекол, достигают диапазона максимальных тепловых флуктуаций внутри вещества, а затем облучают его необходимой энергией из любой части электромагнитного спектра.

3. Способ по п.1, отличающийся тем, что при изменении проводимости вещества его поддерживают в диапазоне максимальных тепловых флуктуаций на время разности потенциалов.

4. Способ по п.1, отличающийся тем, что при разделении компонентов на границе би- и поликомпонентных соединений их сначала облучают энергией в диапазоне максимальных тепловых флуктуаций, а затем подвергают действию импульсных высокочастотных волн или разряду высокоэнергетичного электромагнитного поля.