Способ сжатия и восстановления речевых сообщений

Способ сжатия и восстановления речевых сообщений

Иллюстрации

Показать все

Реферат

Изобретение относится к области электросвязи, а именно к области систем передачи информации по цифровым каналам связи. В частности, предлагаемый способ может быть использован для передачи речевых сообщений по цифровым каналам связи со скоростью 8-16 кбит/с и может быть отнесен к классу способов кодирования формы речевого сигнала.

Известны способы кодирования речевого сигнала на основе дельта-модуляции, адаптивной дельта-модуляции, импульсно-кодовой модуляции, дифференциальной импульсно-кодовой модуляции, метода блочного кодирования с ортогональным преобразованием, см., например, книгу: М.В.Назаров, Ю.Н.Прохоров. Методы цифровой обработки и передачи цифровых сигналов. - М.: Радио и связь, 1985, с.142-160. Недостатком перечисленных выше способов-аналогов является относительно низкая информационная эффективность, под которой понимается достижение определенного качества восстановления речевой информации при заданной скорости передачи. В рассмотренных способах-аналогах приемлемое качество восстановления речевой информации достигается при скорости передачи более 16 кбит/с.

Известен также способ, описанный в патенте России №2152646 А, МПК G10L 3/02 от 10.07.2000 г., который включает идентично выполняемую до начала сеанса связи на передающей и приемной сторонах предварительную генерацию случайной квадратной матрицы размером m×n элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, выполняемые при ведении сеанса связи дискретизацию аналогового речевого сигнала, квантование дискретных отсчетов, формирование исходной матрицы размером N×N элементов, формирование прямоугольных матриц размерами N×m и m×N единичных и нулевых элементов, передачу прямоугольных матриц по каналу связи, прием их на приемной стороне из канала связи, восстановление исходной матрицы размером N×N элементов и преобразование ее в аналоговый речевой сигнал. При этом для формирования исходной матрицы ее элементам присваиваются значения квантованных дискретных отсчетов речевого сигнала.

Общим недостатком перечисленных выше способов-аналогов является относительно низкая устойчивость к ошибкам в цифровом канале связи. Это проявляется в существенных искажениях в восстановленном речевом сигнале при относительно малых коэффициентах ошибок, возникающих под влиянием нестабильности параметров канала связи и представляющих собой инверсию символов в передаваемых цифровых последовательностях.

Наиболее близким по своей технической сущности к заявленному способу сжатия и восстановления речевых сообщений является способ, описанный в патенте России №2244963, МПК G10L 3/02 от 20.01.2005 г.

Известный способ-прототип включает предварительно идентично выполняемые до начала сеанса связи на передающей и приемной сторонах формирование R≥1 матриц разрешенных кодовых групп размерами m_2r×m_1r единичных и нулевых элементов, где r=1, 2,...,R, и генерацию случайной квадратной матрицы размером m×m элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, выполняемые при ведении сеанса связи на передающей стороне дискретизацию аналогового речевого сигнала, квантование дискретных отсчетов, формирование исходной матрицы размером N×N элементов, формирование из элементов R матриц разрешенных кодовых групп прямоугольной матрицы размером N×m и прямоугольной матрицы размером m×N единичных и нулевых элементов, передачу по каналу связи прямоугольных матриц, и на приемной стороне прием прямоугольных матриц из канала связи, исправление в них ошибок, восстановление исходной матрицы и преобразование ее в аналоговый речевой сигнал.

Формирование прямоугольных матриц размерами N×m и m×N единичных и нулевых элементов из элементов R матриц разрешенных кодовых групп выполняют из условия, что где количество групп элементов, называемых -группами, ν-й строки или ν-го столбца соответствующих матриц, формируемых из элементов строк r-й матрицы разрешенных кодовых групп, Выбор значения для ν-й строки прямоугольной матрицы размером N×m не зависит от выбора значения для ν-го столбца прямоугольной матрицы размером m×N элементов.

Для формирования каждой r-той матрицы разрешенных кодовых групп размером m_2r×m_1r единичных и нулевых элементов сначала каждую i-ю строку, где i=1, 2,...,m_2r/2, r-й матрицы разрешенных кодовых групп, формируют в виде i-й дискретной функции Уолша из упорядоченного множества m_2r/2 дискретных функций Уолша длины m_1r, где m_1r=2^u и u=3, 4,..., затем в каждой сформированной строке всем элементам, равным - 1, присваивают значение 0 и каждую (i+m_2r/2)-ю строку r-той матрицы разрешенных кодовых групп формируют путем инверсии каждого элемента i-той строки этой же матрицы, а на приеме для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N×m и m×N единичных и нулевых элементов последовательно выбирают каждую -группу элементов каждой ν-той строки принятой прямоугольной матрицы размером N×m и каждую -группу элементов каждого ν-того столбца принятой прямоугольной матрицы размером m×N элементов, определяют j-тую строку, где j=1, 2,...,m_2r, r-той матрицы разрешенных кодовых групп, у которой расстояние Хэмминга от выбранной -группы минимально, и если минимальное расстояние Хэмминга меньше величины m_1r/4, то каждому элементу выбранной -группы присваивают значение соответствующего элемента j-той строки r-той матрицы разрешенных кодовых групп, иначе выбранную -группу элементов принятых из канала связи прямоугольных матриц сохраняют неизменной.

Для формирования прямоугольных матриц размерами N×m и m×N элементов, у которых соответственно строки и столбцы сформированы из значений элементов строк R матриц разрешенных кодовых групп, на передающей и приемной сторонах идентично генерируют случайный вектор из m элементов, каждый элемент которого принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, случайную ключевую матрицу размерами N×m и случайную ключевую матрицу размерами m×N единичных и нулевых элементов. Затем каждому элементу каждой -группы каждой ν-й строки прямоугольной матрицы размером N×m элементов и каждой -группы каждого ν-го столбца прямоугольной матрицы размером m×N элементов присваивают значение соответствующего элемента первой строки r-й матрицы разрешенных кодовых групп, после чего формируют суммарные матрицы размерами N×m и m×N элементов путем суммирования по модулю два элементов прямоугольных матриц размерами N×m и m×N элементов с соответствующими элементами случайных ключевых матриц размерами N×m и m×N элементов соответственно. Далее преобразуют полученные суммарные матрицы размерами N×m и m×N элементов путем деления элементов каждой строки суммарной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Затем формируют промежуточную матрицу размером N×N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,...,N, суммарной матрицы размером N×m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N×m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m×m элементов, с полученной после преобразования суммарной матрицей размером m×N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m×N элементов, а остальные элементы равны нулю. После перемножения матриц вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N×N элементов и соответствующими элементами исходной матрицы размером N×N. Затем выполняют итерационный цикл. Для этого последовательно в каждой -группе элементов прямоугольных матриц одновременно всем элементам присваивают значения соответствующих элементов поочередно каждой j-й строки r-й матрицы разрешенных кодовых групп, при этом остальные -группы сохраняют неизменными, и формируют суммарные матрицы размерами N×m и m×N элементов путем суммирования по модулю два элементов полученных после изменения элементов -группы прямоугольных матриц размерами N×m и m×N элементов с соответствующими элементами случайных ключевых матриц размерами N×m и m×N элементов соответственно. Полученные суммарные матрицы размерами N×m и m×N элементов преобразуют путем деления элементов каждой строки суммарной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Далее формируют промежуточную матрицу размером N×N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент сумме произведений элементов n-й строки суммарной матрицы размером N×m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N×m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m×m элементов, с полученной после преобразования суммарной матрицей размером m×N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m×N элементов, а остальные элементы равны нулю. Затем вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N×N элементов и соответствующими элементами исходной матрицы размером N×N элементов и вычитают вычисленное значение показателя ошибки из его ранее вычисленного значения. Если полученная разность больше нуля, то сохраняют новые значения элементов изменяемой -группы и показателя ошибки, иначе сохраняют предыдущие значения элементов изменяемой -группы прямоугольных матриц и показателя ошибки. Затем последнее сохраненное в итерационном цикле значение показателя ошибки вычитают из последнего значения показателя ошибки, полученного до начала этого итерационного цикла, и если полученная разность больше нуля, то итерационный цикл повторяют. Сформированные в результате ряда итераций прямоугольные матрицы размерами N×m и m×N элементов передаются по каналу связи. На приемной стороне для восстановления исходной матрицы размером N×N элементов формируют суммарные матрицы размерами N×m и m×N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N×m и m×N элементов с соответствующими элементами случайных ключевых матриц размерами N×m и m×N элементов соответственно. Затем преобразуют полученные суммарные матрицы размерами N×m и m×N элементов путем деления элементов каждой строки суммарной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Далее перемножают диагональную матрицу, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N×m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N×m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m×m элементов, с полученной после преобразования суммарной матрицей размером m×N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m×N элементов, а остальные элементы равны нулю.

Для формирования исходной матрицы размером N×N элементов предварительно формируют вектор спектральных коэффициентов из Z элементов, где Z≥N², путем дискретного косинусного преобразования кодируемого блока из Z квантованных дискретных отсчетов речевого сигнала и выбирают N² элементов вектора спектральных коэффициентов, из которых формируют исходную матрицу. При этом каждому ее элементу A_Ll, где L=1, 2,...,N и l=1, 2,...,N, присваивают значение z-го элемента вектора спектральных коэффициентов, z-й номер которого определяют в соответствии с выражением: z=L+N·(l-1)+D, где D=0, 1,...,10. Ha приемной стороне для преобразования восстановленной исходной матрицы в аналоговый речевой сигнал сначала преобразуют восстановленную исходную матрицу в вектор из Z спектральных коэффициентов, у которого значения N² элементов равны значениям элементов восстановленной исходной матрицы размером N×N элементов, а остальные Z-N² элементов равны нулю, и затем восстанавливают аналоговый речевой сигнал путем обратного дискретного косинусного преобразования полученного вектора из Z спектральных коэффициентов.

Способ-прототип позволяет при заданной пропускной способности канала связи исправлять ошибки и тем самым обеспечить сравнительно высокое качество восстановления речевых сообщений при передаче цифровых последовательностей по каналу связи с относительно большим коэффициентом ошибок.

Недостатком способа-прототипа является относительно низкое качество восстановления сообщений при передаче цифровых последовательностей по каналу без ошибок или по каналу с малым коэффициентом ошибок. Это объясняется следующим.

Во-первых, для кодирования исходной матрицы с целью исправления ошибок используются только разрешенные кодовые комбинации длины m, число которых по сравнению с числом всех возможных комбинаций той же длины тем меньше, чем больше ошибок может быть исправлено в этих комбинациях на приемной стороне. Ограничение на разрешенность кодовых комбинаций приводит к резкому сокращению числа разрешенных вариантов цифрового представления исходной матрицы и к снижению вероятности разрешенности оптимального из всех возможных вариантов.

Во-вторых, использование одной случайной ключевой матрицы размером N×m и одной случайной ключевой матрицы размером m×N, которые для кодирования каждого очередного блока дискретных отсчетов речевого сигнала идентично генерируются на передаче и приеме, не приводит к существенному повышению качества восстановления, поскольку фактически при кодировании исходной матрицы число разрешенных вариантов ее цифрового представления не увеличивается.

Технической задачей является повышение качества восстановления речевых сообщений при обеспечении исправления ошибок, возникающих в передаваемых цифровых последовательностях под влиянием нестабильности параметров канала связи, позволяющее осуществлять ведение телефонных переговоров по низкоскоростным цифровым каналам связи.

Решение технической задачи достигается тем, что в известном способе сжатия и восстановления речевых сообщений, включающем предварительно идентично выполняемые до начала сеанса связи на передающей и приемной сторонах формирование R≥1 матриц разрешенных кодовых групп размерами m_2r×m_1r единичных и нулевых элементов, где r=1, 2,...,R, и генерацию случайной квадратной матрицы размером m×m элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, выполняемые при ведении сеанса связи на передающей стороне дискретизацию аналогового речевого сигнала, квантование дискретных отсчетов, формирование исходной матрицы размером N×N элементов, формирование из элементов R матриц разрешенных кодовых групп прямоугольных матриц размерами N×m и m×N единичных и нулевых элементов, передачу по каналу связи прямоугольных матриц, и выполняемые при ведении сеанса связи на приемной стороне прием прямоугольных матриц из канала связи, исправление в них ошибок, восстановление исходной матрицы и преобразование ее в аналоговый речевой сигнал, вместо неограниченного сверху числа (R≥1) матриц разрешенных кодовых групп до начала сеанса связи на передающей и приемной сторонах формируют две (R=2) таких матрицы, а при ведении сеанса связи на передающей стороне прямоугольные матрицы размерами N×m и m×N единичных и нулевых элементов формируют из элементов только первой матрицы кодовых групп, а также дополнительно предварительно до начала сеанса связи на передающей и приемной сторонах идентично генерируют еще F-1, где F>1, случайных квадратных матриц размером m×m элементов, каждый элемент которых принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, и формируют G>1 случайных ключевых матриц размером N×m и G>1 случайных ключевых матриц размером m×N единичных и нулевых элементов, далее при ведении сеанса связи на передающей стороне при формировании прямоугольных матриц размерами N×m и m×N формируют вектор размером М единичных и нулевых элементов из элементов второй матрицы разрешенных кодовых групп, затем этот вектор передают по цифровому каналу связи вместе с прямоугольными матрицами, а на приемной стороне при ведении сеанса связи дополнительно принимают вектор из канала связи и перед восстановлением исходной матрицы исправляют в нем ошибки.

Для формирования каждой r-той, где r принимает значение 1 или 2, матрицы разрешенных кодовых групп размером m_2r×m_1r единичных и нулевых элементов значения m₂₂ и m₁₂ для второй матрицы (r=2) назначают большими, чем соответствующие значения m₂₁ и m₁₁ для первой матрицы (r=1) разрешенных кодовых групп.

Для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N×m и m×N единичных и нулевых элементов последовательно выбирают каждую m₁₁·p₁-группу элементов, из которых сформированы эти матрицы, определяют j-тую строку, где j=1, 2,...,m₂₁, первой матрицы разрешенных кодовых групп, у которой расстояние Хэмминга от выбранной m₁₁·p₁-группы минимально, и если минимальное расстояние Хэмминга меньше величины m₁₁/4, то каждому элементу выбранной m₁₁·p₁-группы присваивают значение соответствующего элемента j-той строки первой матрицы разрешенных кодовых групп, иначе выбранную m₁₁·p₁-группу элементов сохраняют неизменной. Для исправления ошибок в принятом из канала связи векторе размером М элементов последовательно выбирают каждую m₁₂·p₂-группу элементов этого вектора, определяют j-тую строку, где j=1, 2,...,m₂₂, второй матрицы разрешенных кодовых групп, у которой расстояние Хэмминга от выбранной m₁₂·p₂-группы минимально и каждому элементу выбранной m₁₂·p₂-группы присваивают значение соответствующего элемента j-той строки второй матрицы разрешенных кодовых групп.

Для формирования прямоугольных матриц размерами N×m и m×N и вектора размером М единичных и нулевых элементов из значений элементов строк соответствующих матриц разрешенных кодовых групп предварительно до начала сеанса связи на передающей и приемной сторонах идентично генерируют случайный вектор из m элементов, каждый элемент которого принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, и из значений элементов строк второй матрицы разрешенных кодовых групп формируют матрицу разрешенных векторов размером H×М при условии, что H=(F·G). Далее на передающей стороне сначала из значений элементов строк первой матрицы разрешенных кодовых групп предварительно формируют матрицу разрешенных кодовых комбинаций размером W×m, после чего формируют матрицу предварительных оценок размером W×W×G×F. Затем при ведении сеанса связи формируют оптимальную матрицу соответствия размерами 2×N. Для этого на передающей стороне назначают значение f=0, значение показателя ошибки назначают равным бесконечно большому числу и F раз выполняют большой цикл, в котором назначают значения f=f+1, g=0, и G раз выполняют малый цикл, в котором назначают значение g=g+1, значение промежуточного показателя ошибки назначают равным бесконечно большому числу, формируют матрицу соответствия размерами 2×N, каждый элемент которой равен единице, и выполняют итерационный цикл. В итерационном цикле сначала назначают значение n₁=0 и N раз выполняют первый внешний цикл, в котором назначают значения n₁=n₁+1, w₁=0, и W раз выполняют первый внутренний цикл, в котором назначают значения w₁=w₁+1, значение n₁-ого элемента первой строки матрицы соответствия назначают равным w₁ и вычисляют промежуточный показатель ошибки в виде суммы квадратов разностей между каждым i₁j₁-ым элементом исходной матрицы размером N×N и i₂j₂gf-тым элементом матрицы предварительных оценок размером W×W×G×F, где i₁=1, 2,...,N, j₁=1, 2,...,N, i₂ принимает значение i₁-ого элемента первой строки матрицы соответствия, а j₂ принимает значение j₁-ого элемента второй строки матрицы соответствия. После этого текущее значение промежуточного показателя ошибки вычитают из минимального из всех значений промежуточного показателя ошибки, ранее полученных в текущем малом цикле, и если полученная разность больше нуля, то значение n₁-ого элемента первой строки матрицы соответствия сохраняют. Иначе значение этого элемента назначают равным его предыдущему значению, а затем назначают значение n₂=0 и N раз выполняют второй внешний цикл, в котором назначают значения n₂=n₂+1, w₂=0, и W раз выполняют второй внутренний цикл, в котором назначают значения w₂=w₂+1, значение n₂-ого элемента второй строки матрицы соответствия назначают равным w₂ и вычисляют промежуточный показатель ошибки в виде суммы квадратов разностей между каждым i₁j₁-ым элементом исходной матрицы размером N×N и i₂j₂gf-тым элементом матрицы предварительных оценок размером W×W×G×F, где i₁=1, 2,...,N, j₁=1, 2,...,N, i₂ принимает значение i₁-ого элемента первой строки матрицы соответствия, а j₂ принимает значение j₁-ого элемента второй строки матрицы соответствия. После этого текущее значение промежуточного показателя ошибки вычитают из минимального из всех значений промежуточного показателя ошибки, ранее полученных в текущем малом цикле, и если полученная разность больше нуля, то значение n₂-ого элемента второй строки матрицы соответствия сохраняют. Иначе значение этого элемента назначают равным его предыдущему значению. Далее в итерационном цикле минимальное из всех значений промежуточного показателя ошибки, ранее полученных в текущем итерационном цикле, вычитают из минимального из всех значений промежуточного показателя ошибки, ранее полученных до начала текущего итерационного цикла в текущем малом цикле, и если полученная разность больше нуля, то итерационный цикл повторяют. Иначе выполнение итерационного цикла прекращают и в малом цикле минимальное из всех значений промежуточного показателя ошибки, ранее полученных в текущем малом цикле, вычитают из значения показателя ошибки. Если полученная разность больше нуля, то назначают значения f₀=f, g₀=g, значения элементов оптимальной матрицы соответствия размерами 2×N назначают равными значениям соответствующих элементов матрицы соответствия размерами 2×N, а значение показателя ошибки назначают равным минимальному из всех значений промежуточного показателя ошибки, ранее полученных в текущем малом цикле. Далее после завершения выполнения всех вышеуказанных циклов определяют значение h=(f₀-1)·G+g₀, затем значения элементов вектора размером М назначают равными значениям соответствующих элементов h-той строки матрицы разрешенных векторов размером H×М. Значения элементов каждой i-й строки прямоугольной матрицы размером N×m, где i=1, 2,...,N, назначают равными значениям соответствующих элементов той строки матрицы разрешенных кодовых комбинаций размером W×m, номер которой равен значению i-го элемента первой строки оптимальной матрицы соответствия, а значения элементов каждого i-го столбца прямоугольной матрицы размером m×N, где i=1, 2,...,N, назначают равными значениям соответствующих элементов той строки матрицы разрешенных кодовых комбинаций размером W×m, номер которой равен значению i-го элемента второй строки оптимальной матрицы соответствия.

Для восстановления исходной матрицы размером N×N элементов на приемной стороне сначала определяют h-тую строку, где h=1, 2,...,H, матрицы разрешенных векторов размером H×M, у которой расстояние Хэмминга от принятого из канала связи и исправленного вектора размером М единичных и нулевых элементов равно нулю, и определяют значения f₀ и g₀, где g₀=1, 2,...,G, f₀=1, 2,...,F, из условия h=(f₀-1)·G+g₀. Затем формируют суммарные матрицы размерами N×m и m×N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N×m и m×N элементов с соответствующими элементами g₀-ых ключевых матриц размерами N×m и m×N элементов соответственно. После этого преобразуют полученные суммарные матрицы размерами N×m и m×N элементов путем деления элементов каждой строки суммарной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m×N элементов на сумму единиц соответствующего столбца, перемножают диагональную матрицу размером N×N, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,...,N, суммарной матрицы размером N×m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N×m элементов, с ранее идентично сформированной на передающей и приемной сторонах f₀-ой случайной квадратной матрицей размером m×m элементов, с полученной после преобразования суммарной матрицей размером m×N элементов и с диагональной матрицей размером N×N, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m×N, а остальные элементы равны нулю.

Для формирования матрицы разрешенных векторов размером H×M единичных и нулевых элементов сначала определяют значение p₂=1, 2,... из условий M=m₁₂·p₂ и H=(m₂₂)^p2 а затем образуют все H возможных сочетаний m₁₂·p₂-групп путем присоединения друг к другу р₂ различных или идентичных m₁₂·p₂-групп, каждая из которых состоит из m₁₂ элементов и идентична одной из строк второй матрицы разрешенных кодовых групп. Значения элементов каждой строки матрицы разрешенных векторов размером H×M назначают равными значениям соответствующих элементов одного из H образованных сочетаний m₁₂·p₂-групп, при этом каждое образованное сочетание m₁₂·p₂-групп используют для формирования только одной строки матрицы разрешенных векторов размером H×M.

Для формирования матрицы разрешенных кодовых комбинаций сначала определяют значение p₁=1, 2,... из условий m=m₁₁·p₁ и W=(m₂₁)^p1. Затем образуют все W возможных сочетаний m₁₁·p₁-групп путем присоединения друг к другу p₁ различных или идентичных m₁₁·p₁-групп, каждая из которых состоит из m₁₁ элементов и идентична одной из строк первой матрицы разрешенных кодовых групп. Значения элементов каждой строки матрицы разрешенных кодовых комбинаций размером W×m единичных и нулевых элементов назначают равными значениям соответствующих элементов одного из W образованных сочетаний m₁₁·p₁-групп. При этом каждое образованное сочетание m₁₁·p₁-групп используют для формирования только одной строки матрицы разрешенных кодовых комбинаций размером W×m.

Для формирования каждой из G случайных ключевых матриц размером N×m единичных и нулевых элементов сначала генерируют первую строку этой матрицы, а затем остальные строки назначают поэлементно равными первой, а для формирования каждой из G случайных ключевых матриц размером m×N сначала генерируют первый столбец этой матрицы, а остальные столбцы назначают поэлементно равными первому.

Для формирования матрицы предварительных оценок размером W×W×G×F вычисляют значения каждого ijgf-того элемента этой матрицы, где i=1, 2,...,W, j=1, 2,...,W, g=1, 2,...,G, f=1, 2,...,F. Для этого сначала формируют вектор-строку размером m элементов, в котором каждый элемент получают путем сложения по модулю два элементов i-той строки матрицы разрешенных кодовых комбинаций размером W×m с соответствующими элементами первой строки g-той случайной ключевой матрицы размером N×m, и вектор-столбец размером m элементов, в котором каждый элемент получают путем суммирования по модулю два элементов первого столбца g-той случайной ключевой матрицы размерами m×N с соответствующими элементами j-той строки матрицы разрешенных кодовых комбинаций. Затем перемножают вектор-строку с f-той случайной квадратной матрицей размером m×m и с вектором-столбцом. Полученное после перемножения значение делят на произведение числа единиц в векторе-строке и числа единиц в векторе-столбце. Полученное после деления значение умножают на сумму произведений элементов случайного вектора с соответствующими элементами вектора-строки и на сумму произведений элементов случайного вектора с соответствующими элементами вектора-столбца.

Благодаря новой совокупности существенных признаков не только обеспечивается возможность исправления большого числа ошибок, возникающих в цифровых последовательностях под влиянием нестабильности параметров канала связи, но при этом за счет использования большего, чем один, числа случайных квадратных и ключевых матриц значительно увеличивается число разрешенных вариантов цифрового представления кодируемой исходной матрицы. Таким образом, предлагаемый способ для заданной пропускной способности канала связи позволяет осуществлять выбор оптимального варианта цифрового представления из большего числа разрешенных вариантов, исправлять возникающие ошибки и тем самым существенно повысить качество восстановления речевых сообщений при передаче цифровых последовательностей как по каналу без ошибок, так и по каналу с ошибками.

Проведенный анализ показал, что аналоги, обладающие совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют. Следовательно, заявленный способ соответствует условию патентоспособности "новизна". Поиск известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа, показал, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленный способ соответствует условию патентоспособности "изобретательский уровень".

Заявленный способ поясняется чертежами:

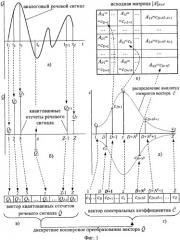
- Фиг.1. Последовательность преобразований аналогового речевого сигнала в исходную матрицу

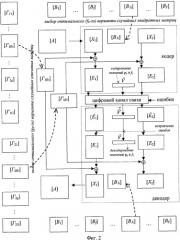
- Фиг.2. Последовательность преобразований исходной матрицы к цифровому виду и обратное преобразование принятого из канала связи цифрового потока в исходную матрицу;

- Фиг.3. Структура матриц разрешенных кодовых групп разрешенных кодовых комбинаций и разрешенных векторов

- Фиг.4. Структура матрицы предварительных оценок

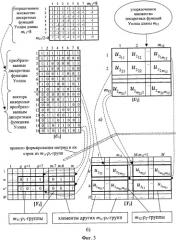
- Фиг.5. Структура оптимальной матрицы соответствия прямоугольных матриц вектора

- Фиг.6. Структура суммарных матриц и преобразованных суммарных матриц

- Фиг.7. Структура диагональных матриц

- Фиг.8. Исправление ошибок в принятых из канала связи прямоугольных матрицах и векторе

- Фиг.9. Последовательность преобразований восстановленной исходной матрицы [A]_N×N в непрерывный речевой сигнал.

Возможность реализации заявленного способа сжатия и восстановления речевых сообщений при сохранении удовлетворительного качества восстановления (разборчивости и узнаваемости речи) при передаче цифровых последовательностей как по каналу без ошибок, так и по каналу с ошибками, объясняется следующим. Существует традиционный подход повышения устойчивости к ошибкам в цифровом канале связи путем использования помехоустойчивых кодов, описанных, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976. Он основан на разделении всех возможных кодовых комбинаций на разрешенные и запрещенные. Такой подход предполагает введение в передаваемую цифровую последовательность дополнительных бит, и чем больше ошибок может исправлять код, тем больше вводится дополнительных бит. Это приводит к существенному снижению степени сжатия передаваемой информации и повышению требований к пропускной способности канала.

Однако ввиду большой избыточности речи, как вида информации, и адаптивного характера кодирования, используемого как в способе-прототипе, так и в предлагаемом способе, при сохранении удовлетворительного качества восстановленной речи возможно ввести существенные ограничения на разрешенность комбинаций элементов цифровых последовательностей с целью исправления ошибок. При этом кардинальным отличием такого подхода от традиционного помехоустойчивого кодирования является то, что дополнительные биты не вводятся и все элементы передаваемой р