Способ идентификации объектов по их описаниям с использованием обобщенной золотой пропорции

Способ идентификации объектов по их описаниям с использованием обобщенной золотой пропорции

Иллюстрации

Показать все

Реферат

Изобретение относится к области информационных технологий и может быть использовано при идентификации и оценке объектов, представленных в виде описаний в заданных предметных областях.

Известны способы идентификации объектов, представленных в информационных базах в виде текстовых описаний или набора информативных слов, которые позволяют на поступивший запрос получить из информационной базы ответ, совпадающий с запросом по набору признаков [1, 2].

Данные способы имеют ограничения по количеству совпадающих параметров текста и запроса, что снижает их эффективность при проведении сопоставительного анализа реальных объектов и их описаний, имеющихся в базах данных.

Известен способ получения модели сознания человека по созданному человеком тексту, включающий формирование лексических и грамматических характеристик текстов, параметров ценности смысловых объектов, лингвистическое преобразование текстов и запросов, обработку запросов и ответов, идентификацию ответов из выбранных информационных баз по совпадению смысловых объектов запросов и предложений в текстовых базах и адресацию полученных ответов в установленные информационные базы [3].

Данный способ направлен на повышение точности идентификации текстовых объектов, но не позволяет извлекать из них новые данные о структуре реальных объектов, которые могли бы повысить эффективность их оценки по текстовым описаниям и использоваться при моделировании информационной деятельности человека.

Известно использование феноменологических и математических свойств обобщенной золотой пропорции при исследовании различных объектов естественного и искусственного происхождения, позволяющих обнаруживать и включать в описания объектов их свойства и характеристики, связанные с устойчивостью, гармонией, изоморфизмом, симметрией и асимметрией, инвариантными и другими отношениями, характеризующими структуру объектов как сложных системных образований [4, с.31-32].

При этом используются следующие понятия, связанные с золотой пропорцией.

1). Классическая пропорция золотого сечения или золотое сечение - иррациональное число α=1,61803398..., которое возникает в результате деления отрезка на две неравные части так, что отношение большей части к меньшей равняется отношению всего отрезка к большей части [5, с.3].

2). Ряды обобщенных чисел Фибоначчи или р-чисел Фибоначчи (р-ряды Фибоначчи), включающих, как частные случаи, двоичный числовой ряд (при р=0), классический ряд Фибоначчи (при р=1), связанный с классической пропорцией золотого сечения, и натуральный ряд чисел (при р=∞), согласно которым существует бесконечно много р-пропорций золотого сечения, названных обобщенной золотой пропорцией α_р (1≤α_р≤2) и представляющих собой новый класс иррациональных чисел [5, с.13-15, 19-21].

Однако получаемые описания не позволяют идентифицировать объекты по значениям обобщенной золотой пропорции α_р и р-чисел Фибоначчи как элементам, характеризующим и раскрывающим взаимосвязи между существенными признаками в описаниях объектов согласно целевым запросам пользователей.

Известно применение в информационных технологиях способов моделирования документальных информационных потоков (ДИП), включающих операции идентификации результатов деятельности с использованием классической золотой пропорции и классического ряда Фибоначчи [6].

Такие способы позволяют получить интегральные, преимущественно статистические, оценки ДИП, но не раскрывают структурные взаимосвязи между документами и описываемыми ими объектами.

Известен способ идентификации формул изобретений с использованием классического золотого сечения, при котором в каждой формуле или их выборке, содержащей ограничительные и отличительные признаки, подсчитывают число словоупотреблений, относящихся к ограничительной и отличительной частям, а также к формуле или выборке в целом, вычисляют доли словесных масс отличительной и ограничительной частей, строят соответствующие статистические распределения, например, в виде графика распределения долей словесных масс отличительной части формулы изобретения, определяют показатели вариации данного распределения: дисперсию, стандартное отклонение и коэффициент вариации, измеряют степень влияния группировочного признака (разброс долей словесных масс отличительной части около золотого сечения) на общую вариацию, измеряют предельную ошибку выборки, определяют доверительный интервал средней доли отличительной части и оценивают степень его близости с теоретическим значением классического золотого сечения, в качестве которого принимают число а=0,618, полученное из решения уравнения а²+а-1=0, причем для дисперсии и стандартного отклонения используют соответственно выражения σ²=а³=0,236 и [7].

Известный способ позволяет по степени концентрации долей словесных масс, например, отличительной части формулы изобретения, около теоретического значения классического золотого сечения, определить степень ее близости с этим значением, но кроме статистических свойств не раскрывает качественные или количественные структурные особенности непосредственно формулы изобретения или выборки формул в их связи с объектами изобретений.

Известен способ идентификации стихотворных произведений по их текстам с использованием обобщенной золотой пропорции как систем, структурными элементами которых являются строки стиха в пределах строфы и строфы в пределах целого произведения. Способ основан на измерении и сопоставительном анализе значений коэффициента вариации ритма. Степень устойчивости ритма оценивают по коэффициенту вариации V_T, который равен отношению стандартного отклонения s к среднему значению ударности структурного элемента (тонической длины строки Т_СТРК, тонического объема строфы Т_СТРФ и тонического объема стиха Т_СТИХ), т.е. V_T=s_T/Т. Значения параметров Т, V_T и s_T рассчитывают отдельно для строк, строф и целых произведений, а средние значения вычисляют на основе индивидуальных данных с учетом количества текстов по каждому варианту их строфической организации. Например, для строф, написанных преимущественно ямбическими стихотворными размерами, проводят сравнение с аналогичными измерениями для «Онегинской строфы» (романа А.С. Пушкина «Евгений Онегин») как эталонной структурой, в которой ритм, рифма и интонация образуют единое целое, а эстетическая значимость такого целого отражается в критерии обобщенной золотой пропорции α_p и р-чисел Фибоначчи [8].

Данный способ ориентирован на оценку степени отклонения реальных параметров стихотворного произведения - сонета от золотой пропорции посредством подсчета специфических его признаков и получения численного значения отклонения. В этом отношении способ дает интерпретационную оценку произведения как результата поэтической деятельности человека.

Наиболее близким к предлагаемому способу по решаемой технической задаче является способ идентификации объектов по их описаниям с использованием обобщенной золотой пропорции, основанный на следующем положении: «...каждый получаемый человеком творческий результат в информационном плане может быть рассмотрен как совокупность существенных признаков, которая в отношении поставленной цели, для достижения которой и был собственно развернут деятельностный процесс, обладает качеством более высоким, нежели все ранее получаемые совокупности аналогичного целевого назначения» [9, с.5]. Это позволяет выделять и идентифицировать каждую такую совокупность существенных признаков среди аналогов.

Способ заключается в том, что в процессе информационной деятельности человека любой объект в заданной предметной области характеризуют понятием - описанием в виде совокупности существенных признаков, разделенной на две группы в отношении целевого запроса пользователя. Например, такими описаниями могут быть формулы изобретений с выделенной отличительной частью. В текстах таких формул одну группу образуют ограничительные, а другую - отличительные признаки, вместе представляющие собой такую совокупность необходимых признаков, которая в отношении цели изобретения или решаемой задачи характеризуется как система с соответствующим этой цели или задаче качеством. Согласно способу аналогичный подход к формированию описаний может быть использован «...в любых видах творческой деятельности, где ссылки на предшествующие публикации образуют своего рода ограничительную (известную) часть получаемого результата» [9, с.6]. Делят в описании число всех существенных признаков на большее из чисел признаков в любой из двух названных групп, а при равенстве числа признаков в группах делят число всех существенных признаков на любое из этих чисел, полученную пропорцию сравнивают с табличными значениями обобщенной золотой пропорции α_р - положительными корнями уравнения Х^p+1-X^p-1=0, вычисленными при заданных значениях р=0, 1, 2, 3,... и определяют ближайшее к нему табличное значение α_р, из выражения ϕ_р(n)=ϕ_р(n-1)+ϕ_р(n-р-1) для обобщенных - р-чисел Фибоначчи, где ϕ_р=1 при n=0, находят табличное число ряда, ближайшее к числу существенных признаков описания и задают по нему диапазон значений параметра р. (Используемый в данном описании символ р принят в литературе по обобщенной золотой пропорции и аналогичен символу S, принятому в [9]).

Согласно способу с использованием полученных значений пропорции и параметра р могут быть исследованы очень большие массивы документов, например десятки миллионов описаний изобретений, т.к. «...на описании каждого изобретения можно проставлять значения α_р, служащие своеобразным «фрактальным индексом» данного изобретения. Особенно интересно иметь такой индекс для тех изобретений по зарубежным патентным формулам, где нет явно выделенной отличительной части (таковы патентные формулы США, Англии, Японии)» [9, с.7]. Для этого значения α_р и р преобразуют в машиночитаемую форму с помощью аппаратурных и программных средств, используемых для работы в электронных системах хранения и обработки информации.

Например, по значениям α_p можно оценивать принадлежность отдельного изобретения и описываемого им объекта, а также их выборок к одной из следующих стадий: проектирование, изготовление, готовый объект. При идентификации объектов - технических решений по формулам изобретений с ограничительной и отличительной частями, включающими существенные признаки как в виде отдельных слов, цифр, так и их сочетаний, показано, что полученные оценки могут использоваться при анализе технического уровня разработок, определении значимости изобретений и возможностей их практической реализации, анализе тенденций и приоритетов в развитии разработок и т.д. [9].

Недостатки известного способа заключаются в следующем.

Идентификация объектов по описаниям, снабженным значениями α_р и р, так же как и по ключевым словам, недостаточно эффективна, т.к. приводит к большому количеству ссылок на запрос в базу данных, что усложняет выбор и оценку объектов.

Если исходить из положения, что зрительное восприятие человека находится на первом месте в ряду ощущений, дающих ему возможность формировать целостный образ объекта, то способ не позволяет получать такое визуальное изображение структуры описания, которое бы наглядно показывало присущие самому объекту геометрические инварианты, связанные с обобщенной золотой пропорцией α_р и р-числами Фибоначчи.

Выявление таких инвариантов путем преобразования описания в наглядный геометрический образ, который может выступать в качестве ассоциативного идентификатора, обеспечивающего возможность быстрого узнавания объекта, позволило бы ускорить процесс идентификации, повысить точность идентификации и эффективность принятия решения об идентификации объекта.

Однако способ не позволяет визуально показать структурные взаимосвязи между существенными признаками в описании объекта, обусловленные наличием в самом объекте свойств и характеристик, связанных с обобщенной золотой пропорцией α_р и р-числами Фибоначчи, что не позволяет осуществлять индексно-графическое кодирование описаний, создавать соответствующие тезаурусы идентификаторов в электронных базах данных и снижает точность идентификации и оценки конкретного объекта по его описанию с помощью обобщенной золотой пропорции α_p и р-чисел Фибоначчи.

Задачей изобретения является разработка способа идентификации объектов по их описаниям с помощью обобщенной золотой пропорции, который не только выявляет некоторые латентные свойства и характеристики исследуемых объектов, но и в сравнении с наиболее близким аналогом позволяет получить технический результат, заключающийся в создании такого геометрического образа каждого описания, который может быть использован в качестве ассоциативного идентификатора со структурой, отображающей в описании связь свойств и характеристик объекта с обобщенной золотой пропорцией α_р и р-числами Фибоначчи, достаточно просто может быть применен для кодирования описаний при их накоплении в электронных базах данных и обеспечивал повышение точности идентификации и оценки каждого объекта по его описанию с помощью обобщенной золотой пропорции α_р и р-чисел Фибоначчи.

Этот технический результат достигается тем, что в известном способе идентификации объектов по их описаниям с использованием обобщенной золотой пропорции, заключающемся в том, что объекты в заданной предметной области характеризуют описаниями в виде совокупности существенных признаков, разделенной в описании каждого объекта на две группы в отношении целевого запроса пользователя, определяют наименьшую по величине пропорцию между общим числом признаков и их числом в любой из групп описания и используют ее при идентификации объекта путем сравнения ее значения со значениями, которые в соответствии с целевым запросом задают на основе табличных значений обобщенной золотой пропорции α_p - одним из положительных корней уравнения Х^р+1-X^p-1=0, вычисленных при р=0, 1, 2, 3,... и в машиночитаемой форме вводят в выбранную базу данных описаний, согласно изобретению в описании дополнительно определяют наибольшую по величине пропорцию между числом признаков в каждой группе и по модулю наименьшего из отклонений названных пропорций от ближайших табличных значений α_p выбирают из них конечное табличное значение α_p с соответствующим ему рядом р-чисел Фибоначчи, определяемым по формуле ϕ_р(n)=ϕ_р(n-1)+ϕ_р(n-р-1), где ϕ_р=1 при n=0, находят член ϕ_р(n)>1, при n=р+1, наименьшее целочисленное значение которого определяют по формуле m=[k-ϕ_р(n)]/ϕ_р(n+1) для n>1, где k - общее число существенных признаков описания, определяют в описании распределение типа «меньшее - большее - всего», соответствующее числу признаков в каждой из двух групп и значению k и отображают его в виде трех последних членов указанного ряда, геометрический образ которого используют в качестве идентификатора, преобразуют его параметры в сигналы, пригодные для машинной обработки, осуществляют кодирование описания и формирование баз данных тезаурусов идентификаторов в системе хранения и обработки информации, при идентификации заданного объекта в запросе к выбранной базе данных указывают желательные параметры идентификатора, характеризующего заданный объект согласно установленным по его описанию значениям параметров, связанных с обобщенной золотой пропорцией α_р и р-числами Фибоначчи, а заключение об идентификации объекта принимают с учетом степени совпадения изображения и параметров идентификатора по запросу с изображениями и параметрами идентификаторов в выбранной базе данных и ассоциативных связей между структурой идентификатора и описанием объекта.

Кроме того, идентификатор может быть изображен в виде дерева.

А также идентификатор может быть изображен в виде диаграммы.

Ниже приведено обоснование существенности отличительных признаков предлагаемого способа для решения поставленной задачи и достижения указанного технического результата.

Табличные значения α_p, являющиеся положительными корнями уравнения Х^p+1-X^p-1=0, при р=0, 1, 2, 3,... находятся в диапазоне 1≤α_р≤2. В этом же диапазоне всегда будут находиться значения пропорции для соотношения в описании признаков типа «всего/большее», т.е. значения наименьшей пропорции. Другая же пропорция между двумя группами признаков типа «большее/меньшее», т.е. наибольшая пропорция, может находиться как в этом же диапазоне, так и может быть значительно больше 2. В последнем случае она не влияет на точность определения табличного значения α_р. Если же она попадает в диапазон между 2 и 1, то возникает необходимость нахождения и выбора одного из двух табличных значений α_р. Такой выбор осуществляют по модулю наименьшего из отклонений каждой из названных пропорций как от первого, так и от второго табличных значений α_р и тем самым определяют соответствующий ему табличный ряд р-чисел Фибоначчи, позволяющий определить диапазон значений параметра n и соответствующий ему диапазон количества существенных признаков описания. Все табличные ряды р-чисел Фибоначчи начинают возрастать с члена ϕ_р(n) при n=р+1 и с увеличением значений р все большее количество начальных членов соответствующих рядов будет равно единице, что выразится во все более одинаковом построении соответствующих геометрических структур. Для того чтобы геометрическая структура наглядно отображала рекурсию соответствующего ряда р-чисел Фибоначчи, для его члена ϕ_р(n) при n=р+1 находят наименьшее целочисленное значение m>1, связанное с числом общих признаков k описания выражением m=[k-ϕ_р(n)]/ϕ_р(n+1) для n>1. Последние три члена такого ряда записывают численно равными распределению существенных признаков типа «меньшее - большее - всего» в описании.

В результате получают начальные условия и конечные ограничения при построении геометрической структуры на основании инвариантов, связанных с обобщенной золотой пропорцией α_p и рядами р-чисел Фибоначчи.

Операции, связанные с выбором табличного значения α_p по двум пропорциям, позволяют более достоверно оценить качество построения описаний объектов, например, с точки зрения возможности изменения содержания и количества существенных признаков, соотношений между объемами совпадающих и отличительных признаков в отношении целевых запросов пользователей и т.д. Такая количественная информация позволяет уточнять содержание описаний и, следовательно, повышать точность их последующей обработки и анализа с помощью обобщенной золотой пропорции α_р и р-чисел Фибоначчи.

Оценка границ структурной устойчивости описаний при таких значениях их внутрисистемных пропорций, которые наиболее близко группируются вокруг определенных, математически устойчивых теоретических значений обобщенной золотой пропорции α_p, играющих роль параметров порядка, позволяет выявлять и такие соответствующие им объекты, которые с большой вероятностью обладают какими-либо более высокими качествами.

Преобразование описания в ряд р-чисел Фибоначчи, а последнего в геометрическую структуру с параметрами, определяемыми выбранными значениями α_p, n, k и отображением в ней распределения существенных признаков типа «меньшее - большее - всего», соответствующего в описании числу признаков в каждой из двух групп и их сумме, позволяет получить геометрический образ описания, содержащий наглядную информацию о структурных особенностях объекта, связанных с обобщенной золотой пропорцией α_p и р-числами Фибоначчи и в явной форме отсутствующих в его описании. Построение геометрической структуры идентификатора в виде дерева или диаграммы основано на принципе ее самотождественного деления как фрактала, структура которого повторяется как на внутриэлементном, так и на системном уровнях. Каждая вершина внутри структуры как «целое» должна делиться на две подвершины, одна из которых тоже как «целое» должна попасть на ближайший нижний уровень, а другая подвершина как «часть» должна попасть на более нижний уровень, номер которого определяется параметром р соответствующего ряда р-чисел Фибоначчи и связанной с ним обобщенной золотой пропорцией α_p. Далее «часть» делится по такой же схеме. Чередование «целое» и «часть» от уровня к уровню приводит к ветвлению структуры и позволяет отображать соотношения между существенными признаками описания [9, с.3, 5, 6].

Идентификаторы с самоподобной рекурсивной структурой, описываемой обобщенной золотой пропорции α_p и р-числами Фибоначчи, позволяют создавать соответствующие тезаурусы и организовывать ассоциативные связи в электронных базах данных описаний в заданных предметных областях. Преобразование изображения идентификатора и соответствующих ему числовых значений параметров в сигналы, пригодные для машинной обработки и индексно-графического кодирования описаний в электронных базах, осуществляют с помощью известных аппаратных и программных средств. Например, в процессе построения изображения дерева или диаграммы с использованием компьютера с операционной средой Windows, снабженного клавиатурой, монитором, манипулятором типа «мышь», носителями файлов обрабатываемых изображений и описаний; в процессе клавиатурного ввода исходных данных в компьютер и построения изображения, например, с помощью программы построения асимметричных АВЛ - деревьев (деревьев Фибоначчи) в среде Turbo Pascal, Visual Basic и др. [10]; в процессе ручного или автоматического ввода исходных данных и построения изображения с помощью систем автоматизированного проектирования; путем введения изображения с бумажного носителя в компьютер с помощью сканера, цифровой фотокамеры и др. технических устройств, обеспечивающих преобразование текстовой и графической информации для их машинного считывания и последующего ввода в базу данных с помощью электронных средств связи. Также описания из вида, воспринимаемого человеком, с помощью известных средств аппаратного и программного обеспечения преобразуют к виду, воспринимаемому ЭВМ, передают сигналы по электронным каналам связи (телефонным, радио, телевизионным и др.) и формируют базы данных описаний, например тематические, предметно-ориентированные и др.

Снабжение каждого описания изображением соответствующего ему идентификатора позволяет задавать при машинном информационном поиске описаний структурно взаимосвязанные друг с другом признаки и повысить тем самым точность идентификации объектов по их описаниям.

В интерактивном режиме, в том числе с использованием существующих баз данных, например, содержащих машиночитаемые описания изобретений, формируется система автоматизированного хранения и обработки информации с базами данных описаний, каждое из которых дополнительно к существующим условным обозначениям снабжается изображением соответствующего идентификатора с параметрами, определяемыми обобщенной золотой пропорцией α_р и р-числами Фибоначчи. На любой стадии поиска и анализа описания с изображениями идентификаторов могут выводиться на экран компьютера. Представление описания с изображением идентификатора дает возможность пользователю визуально воспринимать такое изображение и соотносить его с особенностями структуры объекта, связанными с обобщенной золотой пропорцией. Использование изображения идентификатора как высокоинформативного визуального признака описания в комбинации с числовыми значениями его параметров увеличивает количество совпадающих параметров описания и запроса, что позволяет повысить точность (однозначность) идентификации, проверять адекватность описания как совокупности существенных признаков объекта в отношении целевого запроса пользователя.

По характерному фрагменту идентификатора можно получать выборку описаний объектов, содержащих такой фрагмент и устанавливать ассоциативные связи между структурой идентификатора и семантикой признаков описания. В совокупности с идентификацией по значениям α_p и р-чисел Фибоначчи это позволяет более точно оценивать объекты в заданной предметной области.

Изображение идентификатора в виде дерева или диаграммы позволяет наглядно показывать распределение признаков в описании объекта, а семейства деревьев или диаграмм, сгруппированные по диапазонам заданных значений α_р, могут выступать в качестве баз знаний об объектах самой разной природы, объединенных закономерным единообразием построения их структуры.

Тем самым расширяются возможности проведения сопоставительного анализа разнородных объектов и их оценки по критериям, связанным с обобщенной золотой пропорцией α_р и р-числами Фибоначчи.

Полученные данные могут систематизироваться, дополнять данные других исследований, проводимых в заданных предметных областях, в том числе использоваться в режиме он-лайнового доступа к электронным базам данных через Интернет.

Вышеназванные технические и программные средства, с помощью которых могут реализовываться признаки способа, связанные с машинной обработкой информации, широко используются в информационных технологиях, они не являются предметом притязаний по предлагаемому изобретению и их конкретный вид (тип ЭВМ, операционная система, процессор, объем оперативной и свободной памяти, периферийное обеспечение и др.) выбираются применительно к каждой задаче, на решение которой направлен способ.

В примерах показаны формально-логические операции, касающиеся этих признаков, без детализации технических средств, используемых при их выполнении. Из существующего уровня техники не выявлены объекты, содержащие совокупность заявляемых существенных признаков. Это позволяет считать предлагаемый способ новым. Из существующего уровня техники не известна также совокупность признаков, отличных от признаков способа по ближайшему аналогу. Это позволяет считать предлагаемый способ обладающим изобретательским уровнем.

В таблице 1 приведены значения обобщенной золотой пропорции α_p положительных корней уравнения Х^р+1-X^p-1=0 при р=0, 1, 2, 3,... и соответствующие им числа р-рядов Фибоначчи, полученные по формуле ϕ_р(n)=ϕ_р(n-1)+ϕ_р(n-р-1). Значения α_p приведены с точностью до трех знаков после запятой, достаточной для осуществления предлагаемого способа с приемлемой для идентификации и оценки точностью.

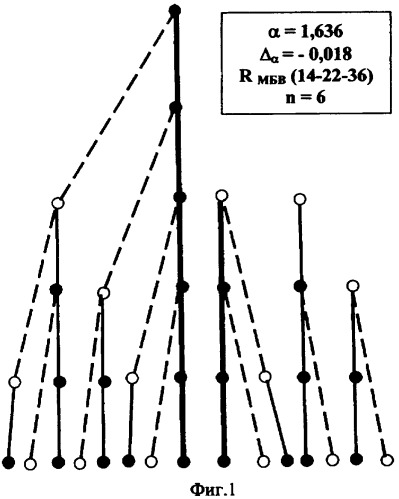
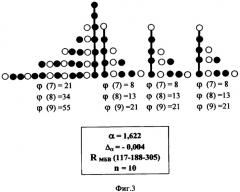
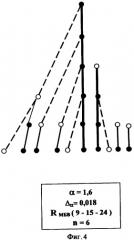
Предлагаемый способ поясняется описанием конкретных примеров его выполнения и прилагаемыми чертежами, где показаны: на фиг.1 - идентификатор в виде дерева с параметрами для описания «Патентная формула»; на фиг.2 - титульный лист к описанию «Патентная формула» с идентификатором в виде дерева; на фиг.3 - идентификатор в виде диаграммы с параметрами для описания «Онегинская строфа»; на фиг.4 - идентификатор в виде дерева с параметрами для описания «Ткань человека»; на фиг.5 - идентификатор в виде диаграммы для описания «Ткань человека».

На фигурах темным цветом обозначены вершины, отвечающие признакам «большее», светлыми окружностями обозначены вершины, отвечающие признакам «меньшее» в изображении идентификатора. Сплошными линями показано деление типа «целое - целое» и «часть - целое», а штриховыми линиями - деление типа «целое - часть» и «часть - часть». Количественные соотношения между вершинами определяются найденными значениями α_p и р-рядов Фибоначчи, приведенными в таблицах к изображениям соответствующих идентификаторов.

Примеры осуществления способа.

Пример 1.

В информационно-поисковую систему ФИПС (Федеральный институт промышленной собственности) Российской Федерации составляют запрос по классу МПК G06F 17/27 «Составы строительных растворов, бетонов, ...содержащие ...портландцементы» и в соответствии с решаемой технической задачей, например, связанной с повышением химической стойкости бетона, из полученного списка выбирают изобретение по патенту RU №2272796 «Бетонная смесь». Формула изобретения представлена следующим текстом: «Бетонная смесь, включающая портландцемент, песок, гравий, комплексную добавку и воду, отличающаяся тем, что содержит в качестве комплексной добавки жидкую фазу полимерно-сульфатного отхода производства тиокола при следующем соотношении компонентов в мас.%: портландцемент 10,4-11,0; песок 28,2-28,4; гравий 54,7-55,4; отход производства тиокола 0,4-0,8; вода - остальное». В этом тексте одну группу составляют признаки ограничительной части: бетонная смесь, портландцемент, песок, гравий, добавка, вода. Количество признаков - 6 шт. («меньшее»). Вторую группу составляют признаки отличительной части: добавка - жидкая фаза, полимер-сульфат, отход производства, тиокол, портландцемент 10,4-11,0, песок 28,2-28,4, гравий 54,7-55,4, отход производства 0,4-0,8, вода - остальное. Количество признаков - 9 шт. («большее»). Общее количество признаков - 15 шт. («всего»), т.е. принимают k=15. Определяют значения следующих параметров описания «Патентная формула»: наименьшую по величине пропорцию, т.е. пропорцию «всего/большее» α_ВБ=15/9=1,667; наибольшую по величине пропорцию, т.е. пропорцию «большее/меньшее» α_БМ=9/6=1,5; распределение R_МБВ «меньшее - большее - всего» в виде последовательности чисел (6-9-15). Находят отклонение найденных пропорций 1,667 и 1,5 от ближайших к ним значений обобщенной золотой пропорции α_p=1=1,618 и α_p=2=1,465, приведенных в таблице 1, следующим образом. Для α_p=1=1,618 находят разности: Δ₁=1,618-1,667=-|0,049| и Δ₂=1,618-1,5=0,118; для α_р=2=1,465 находят разности: Δ₁=1,465-1,667=-|0,202| и Δ₂=1,465-1,5=-|0,035|. Находят максимальные значения: δ_1,618=Δ₂/Δ₁=0,118/0,049=2,408 и δ_1,465=Δ₁/Δ₂=0,202/0,035=5,771. Так как δ_1,618<δ_1,465, то в качестве ближайшего табличного значения обобщенной золотой пропорции выбирают α_p=1=1,618, которому соответствует классический ряд р-чисел Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21,...) при р=1, приведенный в таблице 1. Рекуррентная формула ряда имеет вид ϕ(n)=ϕ(n-1)+ϕ (n-2), где ϕ(0)=ϕ(1)=1. По таблице 1 определяют, что число k=15 общих признаков патентной формулы находится в диапазоне между членами ряда 13 и 21, а параметр n находится в диапазоне от 0 до 7. Для выбора значения n находят производный ряд р-чисел Фибоначчи, в котором член ϕ_р(n)>1, при n=р+1, т.е. ϕ₁(2)=m, где m=[k-ϕ_р(n)]/ϕ_р(n+1) для n>1. Взаимосвязь значений m с членами классического р-ряда Фибоначчи показана в таблице 2. Подставляя в названную формулу последовательно значения: ϕ_p=1 (n=2)=2 и ϕ_p=1 (n=3)=3; ϕ_p=1 (n=3)=3 и ϕ_p=1 (n=4)=5; затем ϕ_p=1 (n=4)=5 и ϕ_p=1 (n=5)=8 из табличного ряда р-чисел Фибоначчи получают для m соответственно значения: 4,333; 2,4 и 1,25. Отклонения среди этих дробных чисел к своему ближайшему целому числу равны: 4,333-4,0=0,333; 2,4-2,0=0,4; 2,0-1,25=0,75 (здесь разность 1,25-1,0 не рассматривают, т.к. при n>1, m не может быть равно 1). По наименьшей величине отклонения 0,333 принимают значение m=4, преобразуют табличный ряд р-чисел Фибоначчи в производный ряд (1, 1, 4, 5, 9, 14), с учетом распределения R_МБВ (6-9-15) корректируют его и получают ряд (1, 1, 4, 6, 9, 15) с членами: ϕ(0)=ϕ(1), ϕ(2)=ϕ(1)+ϕ(0)+2, ϕ(3)=ϕ(2)+ϕ(1)+1, ϕ(4)=ϕ(3)+ϕ(2)-1, ϕ(5)=ϕ(4)+ϕ(3) (см. таблицу 3). Полученные значения с помощью клавиатуры вводят в компьютер и для построения дерева используют, например, следующий программный алгоритм построения ассиметричных АВЛ - деревьев (деревьев Фибоначчи) [10]. Include <iostream.h>; struct Node {int Key; Node* Left; Node* Right;};

class Tree {private: Node* Root;}; public: Tree() {Root=NULL;};

void Print Tree (Node*, int);void FibonTree1 (int., Node**);

void Fibon Tree2 (Node**, int*); Node** GetTree(){return&Root;};

Node* GetTree1() {return Root;}; void Tree:: PrintTree (Node* W, int 1)int i;

if(W!=NULL)Print Tree (W->Right, 1+1); for(i=1; i<=1; i++)cout<<" ";

cout <<W->Key <<endl; PrintTree (W->Left, 1+1);

void Tree:: Fibon Tree1 (int k., Node** T)if(k==0) (*T)=NULL;

else if(k==1 )(*T)=new (Node); (*T)->Left=(*T)->Right=NULL;

else (*T)=new (Node); FibonTree1 (k-1, &((*T)->Left));

Fibon Tree1 (k-2,&((*T)->Right));

void Tree::Fibon Tree2 (Node** T.,int* i) if ((*T)!=NULL)

FibonTree2 (&((*T)->Left), i); (*T)->Key=(*i); (*i)++;

FibonTree2 (&((*T)->Right), i); void main() Tree A; int k;

cout<< "Вводите k..."; cin >> k; int i=1; A.FibonTree1 (k,A. GetTree());

A.FibonTree2 (A.GetTree(),&i); A.PrintTree (A.GetTree1(),0).

Изображение дерева с шестью уровнями, в структуре которого отображены связи между существенными признаками описания «Патентная формула», приведено на фиг.1. Соотношение между вершинами на уровне n=5, отвечает распределению существенных признаков «меньшее - большее - всего» (6-9-15) в объеме формулы изобретения. Этому же распределению отвечает соотношение между вершинами на уровнях n=3, n=4 и n=5. Распределение вершин R_МБВ «меньшее - большее - всего» в объеме дерева имеет вид (14-22-36). Соответствующие пропорции: α_ВБ=36/22=1,636 и α_БМ=22/14=1,571. Область устойчивости дерева находится в окрестности обобщенной золотой пропорции α_p=1=1,618 с минимальным отклонением Δ=α_p=1-α_ВБ=1,618-1,636=-|0,018|. Рассмотрение дерева показывает, что синтез его структуры происходит в соответствии с совпадающими и отличительными признаками формулы изобретения. Машиночитаемое изображение дерева с указанными числовыми обозначениями переносят на титульный лист описания к патенту RU №2272796 «Бетонная смесь» (см. фиг.2) или размещают после текста реферата к патенту и осуществляют его индексно-графическое кодирование в локальной электронной базе данных описаний, которую формируют на основе информационно-поисковой системы ФИПС в соответствии с заданной тематикой.

Задавая в качестве поискового образа параметры дерева с найденными значениями: α_ВБ=1,636, α_БМ=1,571, Δα=-0,018, R_МБВ (14-22-36), n=6 получают возможность использовать изображение дерева в качестве идентификатора, сокращающего количество ссылок на запрос в электронную базу данных, обеспечивающего возможность быстрого выделения описания данной «Бетонной смеси» среди аналогов и рассмотрения особенностей его структуры, связанных с обобщенной золотой пропорцией α_p и р-числами Фибоначчи.

Объект «Бетонная смесь» визуально ассоциируется с древовидной структурой, близкой к эталонной структуре, инвариантной классической золотой пропорции α_р=1=1,618, но несвязность в ней основного и дополнительных поддеревьев на уровне n=0 указывает на нарушение пропорциональности между деревом в целом и его структурно разными частями. Это говорит о том, что среди существенных признаков формулы изобретения отсутствуют признаки, позволяющие на основе единого алгоритма, задаваемого значением α_p=1=1,618, достроить дерево до общей вершины, т.е. получить изображение нового дерева, что должно означать разработку новой бетонной смеси с более взаимосвязанным компонентным составом, направленным в соответствии с целевым запросом пользователя на дальнейшее повышение химической стойкости бетона.

Пример 2.

Исследуют тексты стихотворных произведений строфического типа на основании данных, полученных в [5], где в качестве описаний исследуемых произведений использовались слоговые объемы строф («всего»), включающие определенное количество безударных слогов («большее») и ударных слогов («меньшее»). Таким образом, в пределах строфы выделяют две группы признаков, которые являются не словами, как в примере 1, а они сформированы из ударных и безударных слогов, распределенных в объеме слогов строфы. Четверостишиям 4-стопного ямба соответствует распределение «меньшее - большее - всего» R_МБВ (13-21-34), одической строфе - распределение R_МБВ (33-53-86) и «Онегинской строфе» - распределение R_МБВ (45-73-118). Для этих распределений рекуррентная формула ряда имеет вид ϕ(n)=ϕ(n-1)+ϕ(n-2) при n>1, где ϕ(0)=ϕ(1)=1, ϕ(2)=m. Для 4-стопного ямба по формуле m=[k-ϕ_p(n)]/ϕ_p(n+1) для n>1 находят член ϕ_р=1 (2)=m=2 производного ряда p-чисел Фибоначчи,