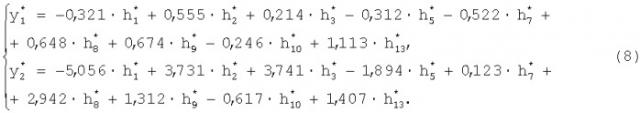Способ диагностирования средств связи телекоммуникационных систем

Способ диагностирования средств связи телекоммуникационных систем

Иллюстрации

Показать все

Реферат

Изобретение относится к технической кибернетике и предназначено для диагностирования средств связи (СС) телекоммуникационных систем (ТКС).

Известен способ диагностирования преддефектного состояния технического объекта (Авторское свидетельство СССР №1596348, кл. G06F 13/46, 1988, Способ диагностирования преддефектного состояния технического объекта), позволяющий определить техническое состояние объекта по анализу сигналов, соответствующих признаку, обладающему максимальной диагностической ценностью среди выбранных признаков состояния объекта.

Недостатком данного способа является возможность определения ложного класса состояний объекта из-за отсутствия учета взаимовлияния между признаками с максимальной диагностической ценностью и другими признаками состояний с возможно близкими значениями диагностических ценностей, таким образом, при значительном сокращении контролируемых параметров достоверность определения класса технического состояния низка.

Наиболее близким по технической сущности является способ диагностирования преддефектного состояния технического объекта (Патент РФ №2050577, кл. G05B 23/02, 1992. Способ диагностирования преддефектного состояния технического объекта), состоящий в том, что для выделенной группы состояний объекта определяют показатель интенсивности связи - эмпирическое корреляционное отношение между значениями сигнала признака с максимальной диагностической ценностью и значениями сигналов остальных признаков состояния. Для каждого класса выбранной группы определяют среднее значение эмпирического корреляционного отношения. Данный способ выбран в качестве прототипа.

Недостатками способа являются необходимость многократного измерения сигналов для всех признаков состояний выбранной группы, что достаточно ресурсоемко, и отсутствие одной из задач диагностики - прогнозирования технического состояния (ГОСТ 20911-89. Техническая диагностика. Термины и определения. М.: Издательство стандартов, 1989. - 14 с.).

Техническим результатом реализации предлагаемого способа является расширение функциональных возможностей в виде выработки прогноза о наступлении предотказового состояния СС ТКС, а также повышение достоверности определения технического состояния многофункциональных средств связи с количеством выходных целевых характеристик более одной, при сокращенном числе подлежащих контролю внутренних параметров средства связи в процессе функционирования.

Этот результат достигается тем, что в способ-прототип, состоящий в том, что среди параметров сложного технического объекта выделяют отдельные параметры, которые являются признаками его технического состояния, сравнивают их с эталонными признаками исходного алфавита классов состояний и по результатам сравнения определяют группу классов возможного технического состояния диагностируемого объекта, в которой определяют признак, имеющий максимальную диагностическую ценность, для всех признаков состояний выбранной группы многократно измеряют сигналы и определяют показатель интенсивности связи - эмпирическое корреляционное отношение значения сигнала с максимальной диагностической ценностью значениям сигналов остальных признаков состояния, проводят вычисление средних значений эмпирического корреляционного отношения для каждого класса и определяют класс в выбранной группе классов состояния с максимально средним значением эмпирического корреляционного отношения, который является фактическим классом состояния, введено то, что всю совокупность как внутренних параметров, так и выходных параметров, определяющих техническое состояние СС ТКС, сокращают за счет выявления сильной корреляционной зависимости отдельно между внутренними параметрами, отдельно между выходными параметрами СС ТКС, из сокращенного множества внутренних и выходных параметров СС ТКС определяют систему регрессионных уравнений, каждое уравнение системы регрессионных уравнений проверяют на адекватность, по заданной достоверности контроля технического состояния с учетом нормированных коэффициентов регрессии в системе регрессионных уравнений осуществляют контроль внутренних параметров СС ТКС с максимальными значениями нормированных коэффициентов регрессии, с учетом динамики изменений выделенных контролируемых параметров осуществляют прогнозирование времени наступления предотказового состояния СС ТКС.

Заявленный способ поясняется чертежами.

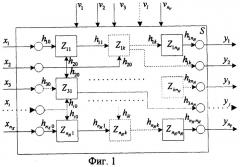
Фиг.1. Структура средства связи телекоммуникационных систем.

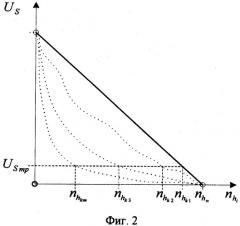
Фиг.2. Зависимость меры неопределенности технического состояния СС ТКС от количества контролируемых параметров.

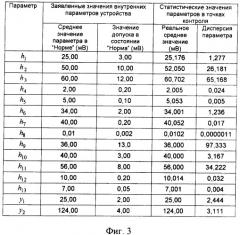
Фиг.3. Заявленные и статистические значения напряжений в точках контроля внутренних и выходных параметров СС ТКС.

Фиг.4. Полуматрица коэффициентов корреляции внутренних параметров.

Фиг.5. Значения соответствия расчетных данных линейного уравнения с выходным параметром у₁ с реальными для десяти контрольных измерений.

Фиг.6. Значения соответствия расчетных данных линейного уравнения с выходным параметром у₂ с реальными для десяти контрольных измерений.

Фиг.7. Значения вкладов в функционирование СС ТКС.

Любое СС ТКС можно структурно формализовать в виде сложной технической системы S (Фиг.1) с множеством величин, описывающих процесс функционирования и образующих в общем случае следующие подмножества:

- совокупность входных параметров системы ;

- совокупность воздействий внешней среды ;

- совокупность внутренних (собственных) параметров системы

;

- совокупность выходных параметров системы .

При этом в перечисленных подмножествах предлагается выделять управляемые и неуправляемые параметры. В общем случае x_i, ν_l, h_k, y_j являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

Процесс функционирования системы S описывается во времени оператором F_S, который преобразует переменные х_i, ν_l, h_k к у_j в соответствии с соотношением вида (Бусленко Н.П. Моделирование сложных систем. Главная редакция физико-математической литературы издательства «Наука», М., 1986. - 356 с.):

Любой элемент сложной технической системы характеризуется следующими множествами: моментов времени T, входных X и выходных Y параметров сигналов, состояний Z. Состояние элемента в момент времени t∈T обозначается как z(t)∈Z, а входные и выходные сигналы - как x(t)∈X и y(t)∈Y соответственно (Советов Б.Я., Яковлев С.А. Моделирование систем: Учебник для вузов / - 4-е изд., стер. - М.: Высшая школа, 2005. - 343 с.).

При задании некоторого правила изменения значений факторов х_i, ν_l существует возможность наблюдать значения выходных параметров у_j. При этом совокупность внутренних параметров системы h_k, изменяясь под воздействием факторов x_i, ν_l, описывает состояние системы в некотором количественном отношении. Так, например, для отдельных блоков, входящих в состав СС ТКС, данная система описания может быть представлена картами напряжений.

Считая, что стохастические воздействия внешней среды оказывают влияние как на внутренние параметры системы h_k, так и на выходные параметры системы у_j, при этом данное влияние для обоих параметров лежит в пределах допустимых значений и позволяет системе функционировать с требуемым качеством от зависимости (1) можно перейти к зависимости вида:

Таким образом, контролируя внутренние параметры системы h_k, можно говорить о качестве функционирования системы в целом и определять ее техническое состояние.

Затраты на проведение полного контроля всех внутренних параметров СС ТКС для определения технического состояния могут быть достаточно большими. В условиях ограниченного ресурса или экономической целесообразности возникает необходимость минимизации множества контролируемых внутренних параметров h_k СС ТКС и определения по их значениям вида технического состояния СС ТКС с требуемой достоверностью.

Способ диагностирования СС ТКС состоит из следующих этапов:

1. Выявление функциональных связей внутренних параметров СС ТКС.

2. Выявление функциональных связей выходных параметров СС ТКС.

3. Определение видов зависимостей несвязанных функционально множественных параметров у_j от m - внутренне независимых параметров h_k.

4. Расчет уравнений регрессии между выходными и внутренними параметрами СС ТКС.

5. Определение k наибольших коэффициентов при внутренних параметрах h_k в системе регрессионных уравнений при достижении требуемой достоверности.

6. Определение новой системы регрессионных уравнений по k наибольшим коэффициентам при внутренних параметрах h_k.

7. Проверка полученных зависимостей на адекватность по выбранным критериям.

8. Набор устойчивого статистического ряда значений выбранных внутренних параметров при k наибольших коэффициентах системы регрессионных уравнений.

9. Построение трендов изменения внутренних параметров h_k по контролируемым данным и прогнозирование значений h_k на n шагов вперед.

10. Определение времени перехода внутреннего параметра по прогнозу значений h_ki в предельное состояние и сигнализация о наступлении предотказового состояния i-того элемента системы через n_i шагов.

Реализацию данного способа осуществляют следующим образом.

На первом этапе из всего множества внутренних параметров сложной технической системы H выявляют внутренние параметры с сильной корреляционной зависимостью , чтобы сократить избыточность в информации о влиянии внутренних параметров на выходные. Для нормального закона распределения наблюдаемых параметров данную зависимость можно определить в соответствии с выражением (Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. - 8-е изд., стер. - М.: Высшая школа., 2002. - 479 с.):

где ;

, - математические ожидания параметров , соответственно;

, - средние квадратические отклонения параметров , ;

K - объем выборки параметров , .

При неизвестном законе распределения наблюдаемых параметров целесообразно использовать характеристики связи, свободные от вида распределения. В частности, одной из данных характеристик является коэффициент ранговой корреляции Спирмена (Статистические методы обработки результатов наблюдений: Учебник для вузов. Под редакцией доктора технических наук профессора Юсупова P.M. - Мин. обороны СССР, 1984. - 687 с.).

По значениям коэффициентов корреляции при заданном уровне достоверности к объемам выборок определяют значимость связи между внутренними параметрами, чем ближе значение коэффициента корреляции к ±1, тем ближе данная связь к линейной функциональной (Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. Примеры и задачи: Учеб. пособие. Под. ред. Кузьмича К.К. - 2-е изд., стер. - Мн.: Новое знание, 2004. - 251 с.).

После расчета парных значений коэффициентов корреляции между выборками внутренних параметров сокращают данные параметры для получения внутренне независимого множества внутренних параметров Н системы по правилу:

1. Пары , разбивают на m-объединений, для которых выполняется условие , где r_mp определяют вероятностью ошибки принимаемого решения;

при отрицательном исходе данной операции считают, что внутренние параметры СС ТКС внутренне независимы;

2. Из m объединений внутренних параметров h_k отбрасывают общий или общие для различных объединений, таким образом сокращают размерность первоначального множества внутренних параметров системы Н до m - внутренне независимых параметров h_k.

Сокращение параметров, находящихся в явной функциональной зависимости, позволяет избежать избыточности статистической информации, заключенной в них.

Второй этап предложенного способа осуществляют аналогично первому этапу.

На третьем этапе осуществляют выбор вида уравнения регрессии (линейного или нелинейного вида), описывающего зависимость несвязанных функционально множественных значений y_j от m - внутренне независимых параметров h_k. Наиболее простым видом зависимости является зависимость линейной регрессии вида (Горковенко В.А., Ткалич О.Б. Методы статистического анализа в задачах планирования и управления НИОКР: Учебное пособие. - Л.: Издание ЛПИ, 1989. - 88 с.):

где b₀, b_i, b_ij - ненормированные коэффициенты регрессии;

h_i, h_j - значения m - внутренне независимых параметров h_k.

Аналогично (4), может быть представлена зависимость несвязанных функционально множественных значений Y от m - внутренне независимых параметров h_k в виде полинома степени m от К факторов (Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. Примеры и задачи: Учеб. пособие. Под. ред. Кузьмича К.К. - 2-е изд., стер. - Минск.: Новое знание, 2004. - 251 с.):

Выполнение четвертого этапа предлагаемого способа сводится к расчету коэффициентов регрессии внутренних параметров h_k на отклик у_i. Для получения коэффициентов в уравнениях регрессии, позволяющих оценить вклад каждой независимой переменной h_k в предсказание зависимой переменной y_i, осуществляют стандартизацию как внутренних параметров, так и выходных параметров СС ТКС. В результате стандартизации параметров получаются параметры , . Одним из видов стандартизации данных величин является преобразование вида (Статистические методы обработки результатов наблюдений: Учебник для вузов. Под редакцией доктора технических наук профессора Юсупова P.M. - Мин. обороны СССР, 1984. - 687 с.):

где - среднеквадратичное отклонение величин h_i;

- математическое ожидание;

h_i - текущее значение величины.

В результате стандартизации параметров получают нулевые средние и единичные стандартные отклонения для выборок наблюдаемых параметров. Процедура стандартизации величин также позволяет избавиться от постоянной составляющей b₀ в уравнении регрессии и перейти от уравнения (5) к виду:

Чем больше абсолютное значение коэффициента регрессии, тем больший вклад в предсказание значения выходного параметра вносит внутренний параметр при коэффициенте β (Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. Примеры и задачи: Учеб. пособие. Под ред. Кузьмича К.К. - 2-е изд., стер. - Мн.: Новое знание, 2004. - 251 с.).

Пятый этап заключается в том, что выделяют из всех коэффициентов регрессии β, входящих в систему регрессионных уравнений, минимальное количество коэффициентов с наибольшими абсолютными значениями k, при сохранении требуемого уровня достоверности в предсказании выходных величин.

На шестом этапе рассчитывают новую систему уравнений регрессии для внутренних параметров при коэффициентах регрессии β, выявленных в результате пятого этапа.

На седьмом этапе осуществляют проверку рассчитанных зависимостей на адекватность по критериям, в качестве которых могут выступать критерии Фишера и Кохрена (Горковенко В.А., Ткалич О.Б. Методы статистического анализа в задачах планирования и управления НИОКР: Учебное пособие. - Л.: Издание ЛПИ, 1989. - 88 с.). При наличии отрицательного исхода данной проверки осуществляют переход к пятому этапу, где осуществляют увеличение k выделенных наиболее влиятельных внутренних параметров на выходные до (k+1) и далее осуществляется повтор шестого этапа. При положительном исходе проверки на адекватность полученной системы уравнений регрессии осуществляют восьмой этап способа диагностирования ССТКС.

На восьмом этапе за определенное время осуществляют измерение k внутренних параметров, входящих в систему регрессионных уравнений. По результатам данных измерений накапливают статистики для каждого из k наблюдаемых внутренних параметров. Контролируемые параметры соответствуют конкретным значениям физических величин, а их измерение осуществляется при помощи технических средств измерения.

На девятом этапе по накопленным статистикам для k наблюдаемых внутренних параметров осуществляют построение трендов изменения данных внутренних параметров h_k, а с учетом динамики изменения трендов определяют прогнозируемые значения h_k на заданное количество временных отсчетов вперед. Порядок построения трендов (действия) по статистике количественных значений физической величины для прогнозирования предлагается выполнять согласно (Рабочая книга по прогнозированию. Под ред. И.В.Бестужев-Лада - М.: Мысль. 1982. С.132 - 178).

На десятом этапе определяют время перехода k_i-го внутреннего параметра по прогнозу значений h_ki в предотказовое состояние k_i-го элемента СС ТКС через n_i временных отсчетов. При этом момент времени, когда контролируемый параметр в стабильной тенденции изменения (тренда) достигает границы, отделяющей значения нормы для этого параметра, соответствует по времени прогнозному времени наступления предотказового состояния СС ТКС.

В результате наблюдений тринадцати внутренних и двух выходных параметров - значений напряжения в точках контроля приемопередающего устройства были получены статистические результаты, представленные на фиг.3.

В соответствии с выражением (3) были получены коэффициенты корреляции между внутренними параметрами сложной технической системы, представленные на фиг.4.

Данные, представленные на фиг.4, показывают, что сильной корреляционной зависимостью обладают внутренние параметры h₁₃ с параметрами h₁₂, h₁₁ и h₄, параметры h₁₀ с параметрами h₁₁, параметры h₁₂ с параметрами h₄ и h₆. Таким образом, общее количество внутренних параметров, с учетом малой взаимной корреляции внутренних параметров h₁₃ и h₁₀, можно выразить через два внутренних параметра h₁₃ и h₁₀, а не через шесть, как это планировалось сначала. Малое значение взаимной корреляции выходных параметров y₁ и у₂, равное -0,0403, позволяют сделать вывод об отсутствии линейной функциональной зависимости между этими параметрами.

Далее, после сокращения внутренних параметров, которые имеют корреляцию на уровне ±0,71 и больше, переходим к нахождению зависимости выходных параметров от оставшихся в анализе внутренних параметров, т.е. находим уравнение регрессии или систему уравнений регрессии для несвязанных линейно-множественных значений Y.

Первичная система уравнений регрессии с нормированными коэффициентами регрессии после выполнения расчетов по (5-7) будет иметь вид

Выполнение этапов с пятого по седьмой предлагаемого подхода позволит преобразовать систему регрессионных уравнений (8) к виду

Таким образом, для наблюдения за техническим состоянием рассмотренного средства связи с двумя выходными параметрами у₁ и у₂ возможно сократить количество контролируемых внутренних и внешних параметров с 15 до 10, то есть на 33,33% процента.

Результаты проверки на адекватность рассчитанной системы линейных уравнений реальным значениям выходных параметров методом подстановки представлены на фигурах 6 и 7.

С учетом полученных результатов можно сделать вывод о пригодности рассчитанной системы регрессионных уравнений для описания зависимости внешних параметров от внутренних параметров СС ТКС.

Таким образом, адекватная информация о состоянии сложного технического средства с более чем одной выходной целевой характеристикой заключена не в одном параметре с максимальной диагностической ценностью как в способе-прототипе, а в совокупности выходных параметров и внутренних параметров по предлагаемому способу, обеспечивающему большую достоверность определения технического состояния средства связи по сравнению со способом-прототипом.

С учетом выражения (9) о пригодности нормированных целевых параметров значениям технической документации можно судить по значениям восьми нормированных внутренних параметров. Другими словами измерение каждого из восьми выделенного по способу параметра, накопление по каждому из них статистики, реализованное в способе по пункту 8, позволит осуществить процедуры построения трендов изменения для каждого из этих параметров по пункту 9 предлагаемого способа. По пункту 8 следует особо отметить, что контролируемые параметры соответствуют конкретным значениям физических величин, а их измерение осуществляется при помощи технических средств измерения. По полученным трендам для каждого из восьми параметров в процессе функционирования средства связи определяется момент времени, когда один или более из восьми контролируемых внутренних параметров окажутся вне зоны нормы, для каждого из них. При сохранении тенденции изменений контролируемых параметров в соответствии с полученными трендами моменты времени, определенные по пункту 10, соответствуют прогнозному времени наступления предотказового состояния СС ТКС.

Эффективность способа диагностирования СС ТКС предлагается оценивать через меру неопределенности технического состояния - U_S (от англ. Uncofigured state - неопределенное состояние) при ограничениях на затраты ресурсов, отводимых на реализацию данного процесса. Количественные значения меры неопределенности технического состояния СС ТКС изменяются в процентном отношении от 100% до 0%. При этом, чем меньше величина меры неопределенности технического состояния СС ТКС, тем с более высокой достоверностью определено техническое состояние СС ТКС.

Принимая во внимание допущение, что каждый элемент вносит в результат функционирования СС ТКС равный вклад, можно определить зависимость меры неопределенности технического состояния U_S от количества контролируемых внутренних параметров . Вид данной зависимости графически представлен на фиг.2 отрезком АВ, где числовые значения меры неопределенности технического состояния U_S варьируются от единицы до нуля, а количество контролируемых элементов от нуля до максимального числа элементов , входящих в состав СС ТКС.

Аналитическая запись данной зависимости имеет вид:

где - количество контролируемых внутренних параметров СС ТКС;

- количество всех внутренних параметров СС ТКС.

Так, например, если техническая система состоит из 100 элементов и контролю подвергается лишь одна треть элементов, вносящих равный вклад в процесс функционирования данной системы, то мера неопределенности ее технического состояния, в соответствии с (10), составит 0,7 или 70%.

В случае, когда отдельные элементы СС ТКС вносят в результат функционирования системы неравномерный вклад, зависимость меры неопределенности технического состояния U_S от количества внутренних параметров примет нелинейный характер. Каждая кривая линия данной зависимости (на фиг.2 они представлены пунктирными изогнутыми линиями) в этом случае будет соединять точки А и В, при этом лежать в пределах треугольника АОВ.

Аналитическая зависимость, в отличие от (10), примет вид:

где - вклад внутреннего элемента с параметром h_i в результат функционирования СС ТКС;

- количество однотипных по вкладу элементов с параметрами h_i в результат функционирования СС ТКС;

K - количество контролируемых внутренних параметров СС ТКС;

N - количество всех внутренних параметров СС ТКС.

В процессе определения технического состояния СС ТКС надсистемой задается требуемое значение меры неопределенности технического состояния системы , для достижения которого необходимо проконтролировать как минимум К внутренних параметров. Другими словами сумма вкладов внутренних элементов с параметрами h_i в результат функционирования СС ТКС должна составлять величину, сравнимую со значением .

С учетом приведенных положений способы, использующие параметр или сигнал с максимальной диагностической ценностью в качестве контрольного, допустимы только для систем, где вклад данного элемента или подсистемы уже составляет значение .

Предлагаемый подход позволяет выявить вклады внутренних элементов с параметрами h_i в результат функционирования СС ТКС расчетом нормированных коэффициентов регрессии β_i. При увеличении контролируемых параметров до К внутренних параметров позволяет применять его для диагностирования современных СС ТКС, являющихся сложными техническими системами.

В качестве показателя, определяющего затраты ресурсов на реализацию способа диагностирования технического состояния сложных технических систем, можно определить требуемое время диагностирования СС ТКС t_тр. Численное значение данного показателя в технологическом аспекте зависит от длительности процессов, лежащих в основе диагностирования СС ТКС.

В общем случае эффективность можно определить как соотношение получаемого эффекта от реализации данного способа и затрат на его реализацию (Петухов Г.Б. Основы теории эффективности целенаправленных процессов. - Мин. обороны СССР, 1989. - 660 с.).

Предполагается эффект выражать через меру неопределенности технического состояния U_S СС ТКС, а затраты - временем определения технического состояния СС ТКС t_mp. Наиболее эффективным будет способ с минимальной мерой неопределенности технического состояния U_S СС ТКС при заданном времени определения технического состояния СС ТКС t_mp.

Так для СС ТКС, состоящего из шести элементов, вносящих неравномерный вклад в его функционирование, представлены на фиг.7.

Подставляя данные значения в выражение (11), получим для способа-прототипа значение меры неопределенности технического состояния, равное:

тогда как предлагаемый подход обеспечит значение равное:

Так как мера неопределенности технического состояния СС ТКС получается при применении предлагаемого способа меньше по сравнению с аналогичными при равных затратах временного ресурса на процесс диагностирования, следовательно, можно считать предлагаемый способ более эффективным.

Проведенный анализ существующих способов позволил установить, что аналоги, тождественные признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна». Введенные отличительные признаки: обеспечения требуемого уровня достоверности определения технического состояния многофункциональных средств связи с количеством выходных целевых характеристик более одной, при сокращенном числе подлежащих контролю внутренних параметров средства связи в процессе функционирования, а также реализация функции прогнозирования наступления предотказового состояния СС ТКС в аналогах не встречаются. Следовательно, заявляемый способ удовлетворяет критерию «изобретательский уровень».

Промышленная применимость способа заключается в возможности его использования для диагностирования средств связи в отрасли телекоммуникаций и реализации этапов способа на существующей в настоящее время элементной базе.

Способ диагностирования средств связи телекоммуникационных систем (СС ТКС), состоящий в том, что среди параметров сложного технического объекта выделяют отдельные параметры, которые являются признаками его технического состояния, сравнивают их с эталонными признаками исходного алфавита классов состояний и по результатам сравнения определяют группу классов возможного технического состояния диагностируемого объекта, отличающийся тем, что всю совокупность как внутренних параметров, так и выходных параметров, определяющих техническое состояние СС ТКС, сокращают за счет выявления сильной корреляционной зависимости отдельно между внутренними параметрами, отдельно между выходными параметрами СС ТКС, из сокращенного множества внутренних и выходных параметров СС ТКС определяют систему регрессионных уравнений, каждое уравнение системы регрессионных уравнений проверяют на адекватность, по заданной достоверности контроля технического состояния с учетом нормированных коэффициентов регрессии в системе регрессионных уравнений осуществляют контроль внутренних параметров СС ТКС с максимальными значениями нормированных коэффициентов регрессии, с учетом динамики изменений выделенных контролируемых параметров осуществляют прогнозирование времени наступления предотказового состояния СС ТКС.