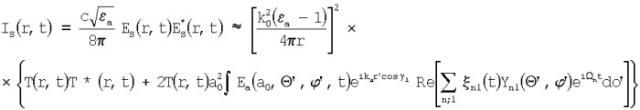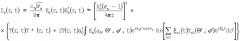Способ определения параметров дисперсных частиц

Способ определения параметров дисперсных частиц

Иллюстрации

Показать все

Реферат

Изобретение относится к контрольно-измерительной технике, в частности к оптическим дистанционным методам контроля, и предназначено для автоматизации процесса измерения размеров и числа частиц в проточных средах, в объемах технологических тепло-, массообменных аппаратов, для оценки качества и эффективности технологических процессов. Предлагаемый способ позволит повысить точность измерений непосредственно в объемах технологических аппаратов, получать информацию о размерах каждой регистрируемой частицы и автоматизировать обработку результатов измерений.

Известен фотоэлектрический способ измерения размеров и концентрации взвешенных частиц [1], заключающийся в том, что в потоке частиц, освещенном неподвижным пучком света, возбуждают акустическое колебание в направлении, перпендикулярном направлению потока и оси пучка, и регистрируют "пачки" импульсов рассеянного частицами света, возникающие при пересечении пучка света колеблющимися частицами, по амплитудам которых судят о размерах частиц, а по средней частоте повторений "пачек" - о концентрации частиц. Недостатком данного способа является применимость его только для контроля взвешенных частиц, отсутствие информации о форме частицы, способ неприменим в случае большой концентрации частиц.

Способ определения параметров дисперсных частиц по [2] заключается в учете эффекта рефракции в исследуемой среде при формировании зоны измерений, причем регистрацию световых импульсов, обусловленных прохождением частиц зоны измерений, проводят в проходящем излучении. К недостаткам данного способа можно отнести сложность аппаратурного оформления способа, трудоемкость его реализации для измерения и контроля параметров реально протекающего технологического процесса.

Известен способ определения параметров дисперсных частиц [3, прототип], заключающийся в том, что объем с дисперсными частицами зондируют пучком маломощного лазерного излучения. Излучение, отраженное частицами назад, оптически смешивают с зондирующим измерением, регистрируют частотный спектр биений, из которого находят распределение частиц по скоростям, затем одновременно с зондирующим лазерным излучением счетный объем подвергают воздействию мощного лазерного импульса на длине волны, отличной от длин волны зондирующего лазера. По изменению частотного спектра биений отраженного зондирующего лазерного излучения определяют распределение частиц по размерам. К недостаткам можно отнести: использование мощной, дорогостоящей лазерной установки, сложность реализации и сложность обработки результатов измерений при большом количестве частиц в среде.

Предлагаемый способ позволит повысить точность измерительной информации о параметрах дисперсных частиц для систем газ-жидкость и жидкость-жидкость в технологических тепло-, массообменных аппаратах, в проточных средах и позволит создавать системы автоматического дистанционного контроля и диагностики дисперсных сред. Данный способ может быть использован при определении поверхности контакта фаз агрессивных сред и в области потенциально опасных технологий.

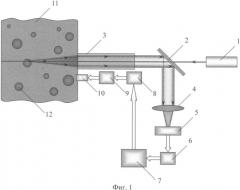
Принцип работы предлагаемого технического решения поясняется с помощью структурной схемы устройства для определения параметров дисперсных частиц, реализующего предлагаемый способ и представленного на фиг.1.

Устройство, реализующее способ, содержит лазер 1 в качестве источника зондирующего излучения; светоделитель (полупрозрачное зеркало) 2; регулярный многоэлементный световод 3; объектив 4; фотоприемник 5; модуль быстродействующего аналого-цифрового преобразователя 6; управляющую электронно-вычислительную машину (ЭВМ) 7; модуль быстродействующего цифроаналогового преобразователя 8; ультразвуковой генератор 9; излучатель ультразвуковых колебаний 10.

Способ осуществляют следующим образом. Исследуемая дисперсная система контактирует с многоволоконным регулярным световодом 3 и излучателем ультразвуковых колебаний 10. Зондирующее излучение с длинной волны λ генерируется лазером 1. Через светоделитель 2 зондирующее излучение посредством многоэлементного световода 3 подводится к дисперсионной среде (сплошной фазе) 11. При прохождении этой волны через исследуемую дисперсную систему происходит рассеяние, отражение и поглощение излучения. Рассеянное и отраженное (под малыми углами относительно направления распространения) от дисперсных частиц 12 излучение проходит через многоэлементный световод 3 и попадает на светоделитель 2, который направляет его на объектив 4. Объектив 4 проецирует излучение непосредственно на фотоприемник 5. Далее аналоговый сигнал с фотоприемника преобразуется к цифровому виду при помощи модуля быстродействующего аналого-цифрового преобразователя 6 и поступает для дальнейшей обработки и регистрации на ЭВМ 7. ЭВМ координирует работу всех узлов системы, а именно: управляет процессом оцифровки сигнала с фотоприемника, посредством цифроаналогового преобразователя 8 управляет работой ультразвукового генератора 9, обрабатывает и регистрирует результаты измерений. На ЭВМ, используя математическую модель [4, 5, 6], согласно оптимальному взаимодействию ультразвуковых колебаний с дисперсными частицами рассчитывают параметры воздействующих импульсов таким образом, чтобы колебания поверхности дисперсной частицы происходили по гармоническому закону с собственной частотой f_n. При этом учитывают физические свойства дисперсной системы и характерное время затухания колебаний дисперсных частиц за счет вязких сил.

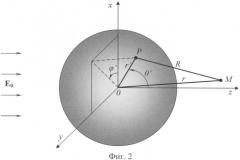
На фиг.2 показана геометрическая схема взаимодействия зондирующего излучения с колеблющимися дисперсными частицами. На колеблющуюся частицу с диэлектрической проницаемостью ε_a в положительном направлении оси Z падает плоская линейно поляризованная электромагнитная волна:. Форма частицы слегка отлична от сферы и изменяется во времени. Частица находится в начале декартовой системы координат (x, y, z). Показаны также сферические координаты точки Р внутри частицы (r', Θ', ϕ'). M - точка наблюдения с координатами (r, Θ, ϕ). Интенсивность рассеянной волны, записанная с точностью до квадратичных членов [5]:

,

где ;

с - скорость света в вакууме;

ε_a - диэлектрическая проницаемость вещества частицы;

E_S(r',t) - рассеянное электромагнитное поле;

Е_a(r',t) - электромагнитное поле в частице при отсутствии возмущений сферической поверхности;

a₀ - радиус невозмущенной капли;

k_а=m_ak₀ - волновое число внутри частицы (m_a - показатель преломления дисперсных частиц);

ξ_n - сферические функции Риккати-Бесселя;

Y_nl(Θ',ϕ') - сферические функции;

do'=sinΘ' dΘ' dϕ'.

Данное выражение показывает, что интенсивность рассеянного электромагнитного поля на комбинационных частотах зависит от квадрата радиуса частицы и амплитуды деформаций ее поверхности. Временная зависимость I_S(t) определяется суперпозицией колебаний на собственных частотах частицы. Колеблющиеся дисперсные частицы можно считать рассеивателями с динамически изменяющейся формой поверхности.

В случае жидкой дисперсной частицы собственные частоты механических колебаний частицы однозначно связаны с ее размером и физическими свойствами дисперсной системы [4]. Таким образом, при измерении частоты собственных колебаний капель по динамической составляющей рассеянного и отраженного ими излучения зондирующего пучка, становится возможным осуществить диагностику функции распределения частиц по размерам. Собственная частота гидродинамических колебаний капли определяется из соотношения [5]:

где n=2,3,... - номер колебательной моды;

β - коэффициент поверхностного натяжения жидкости;

ρ_a - плотность жидкости;

a₀ - радиус невозмущенной капли.

Затухание высокочастотных гармоник с течением времени происходит достаточно быстро, и их влияние на общую картину деформаций жидкой частицы проявляется только на начальном этапе колебаний. Характерное время затухания колебаний за счет вязких сил [5]:

,

где ν - кинематическая вязкость жидкости.

При импульсном воздействии локальные деформации поверхности жидкой частицы, первоначально вызываемые высокочастотными колебательными модами, в дальнейшем развиваются в эллипсоидальные колебания на основной частоте:

Основную частоту f₂ колебаний дисперсной частицы рассчитывают с использованием математической модели взаимодействия зондирующего излучения с колеблющимися дисперсными частицами [7] по временной зависимости уровня принимаемого рассеянного излучения зондирующего пучка, а радиус невозмущенной капли определяют из соотношения:

Интенсивность зондирующего излучения выбирают таким образом, чтобы его воздействие на дисперсные частицы было незначительным.

С ростом размера капли увеличивается время t_ст выхода амплитуды колебаний на стационарный режим (эллипсоидальные колебания на основной частоте) по отношению к периоду основного колебания Т₂. Установление собственных колебаний [5] для малых частиц (радиус которых не превышают 1 мкм) происходит фактически за один период колебаний на основной частоте (t_ст≈Т₂), а для частиц с радиусом больше 15 мкм требуется уже 4-5 периодов. С увеличением размера дисперсной частицы изменяется и характер колебаний. Их форма становится достаточно сложной, и гармонические составляющие колебаний на резонансной частоте прослеживаются неявно. При увеличении размера частицы уменьшается частотный интервал между соседними модами, и, следовательно, большее количество собственных мод принимает участие в формировании возмущения поверхности частицы. Колебания крупных частиц представляют собой суперпозицию колебаний на разных собственных резонансных частотах.

Предлагаемый способ может применяться для анализа и объективного контроля дисперсных систем газ-жидкость и жидкость-жидкость. Применение для обработки сигнала ЭВМ позволяет получать информацию о геометрических параметрах каждой регистрируемой частицы.

Данный способ успешно реализован и применяется в лабораторной практике в Бийском технологическом институте Алтайского государственного технического университета им. И.И.Ползунова для автоматического дистанционного контроля и диагностики дисперсных сред.

Источники информации

1. Патент SU № 1520399, G01N 15/02.

2. Патент SU № 1408304, G01N 15/02.

3. Патент SU № 1508742, G01N 15/02 (прототип).

4. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988, 735 с.

5. Ю.Э.Гейнц, А.А.Землянов, В.Е.Зуев, А.М.Кабанов, В.А.Погодаев. Нелинейная оптика атмосферного аэрозоля. - Новосибирск: Изд-во СО РАН, 1999. - 260 с.

6. Гершгал Д.А., Фридман В.М. Ультразвуковая аппаратура промышленного назначения, изд. 2-е, переработанное и дополненное. М.: Энергия, 1967.

7. Землянов А.А., Гейнц Ю.Э. Вынужденное рассеяние света сферическими частицами //Оптика атмосферы и океана. 1997. Т.10. №4-5. С.500-515.

Способ определения геометрических параметров дисперсных частиц, включающий зондирование исследуемой дисперсной среды пучком маломощного лазерного излучения, регистрацию рассеянного и отраженного дисперсными частицами излучения, отличающийся тем, что исследуемый объем дополнительно подвергают воздействию импульсов ультразвуковых колебаний, по динамической составляющей рассеянного и отраженного под малыми углами относительно направления распространения дисперсными частицами излучения, определяют их собственные частоты механических колебаний и находят размер частиц.