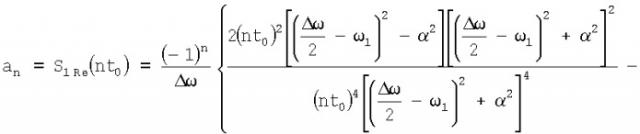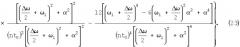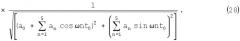Способ передачи и приема сигналов

Способ передачи и приема сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к технике формирования (передачи), приема и обработки электрических сигналов и может быть использовано в системах передачи информации и в других радиотехнических системах, в которых требуется минимизировать структурную (частотно-временную) избыточность информационных сигналов.

Актуальность данной проблемы обусловлена непрерывно возрастающим количеством радиоэлектронных средств (РЭС) различного функционального назначения, требующих соответствующего частотно-временного ресурса (ЧВР), и обеспечения их эффективной электромагнитной совместимости (ЭМС) (Соловьев В.В., Яньшин С.Н. Оценка резерва ресурса при частотном планировании. // Радиотехника, 2003, № 12). Решение этой проблемы, в принципе, возможно, поскольку скорости передачи информации при заданном качестве ее приема в реальных радиотехнических системах (РТС) значительно меньше пропускной способности соответствующих каналов связи, определяемой известным пределом Шеннона.

Основным направлением повышения эффективности использования пропускной способности каналов связи является отыскание соответствующих преобразований источников сообщений, устраняющих их информационную избыточность и поиск сигналов, отображающих эти сообщения, обладающих минимальной структурой (частотно-временной) избыточностью (Финк Л.М. Теория передачи дискретных сообщений. - М.: Сов. радио, 1970. - С.70-77).

В фундаментальном плане для различных источников сообщений и различных каналов связи эта задача не решена.

Наиболее близким к предлагаемому является классический способ передачи и приема сигналов, включающий формирование некоторого сигнала S(t) конечной длительности с соответствующим спектром S(jω), отображающего фрагмент передаваемого сообщения. Поскольку данный сигнал, как и все реальные сигналы, имеет конечную длительность, то, следовательно, он имеет, по крайней мере, теоретически бесконечно протяженный спектр, который при передаче и приеме ограничивается эффективной полосой частот выделенного канала связи. Затем полученный сигнал передается по соответствующему каналу связи на приемную сторону, где он фильтруется от помех в той же полосе частот и обрабатывается соответствующим образом с целью извлечения содержащейся в нем информации (Д.Миддлтон. Введение в статистическую теорию связи. Том 1. - М.: Сов. радио, 1961. - С.107).

Известно, что любой физически реализуемый сигнал имеет комплексный спектр, содержащий вещественную Re(ω) и мнимую Jm(ω) компоненты, которые однозначно связаны преобразованием Гильберта, так как удовлетворяют всем требованиям этого преобразования (Вакман Д.Е., Седлецкий P.M. Вопросы синтеза радиолокационных сигналов. - М.: Сов. радио, 1973. - С.298-300). При этом сигналы - как функции времени, соответствующие вещественной и мнимой частям спектра, являются ортогональными функциями на всей временной оси, сумма которых однозначно определяет исходный физический сигнал. В этом случае сигналы, соответствующие вещественной и мнимой частям спектра, для положительного времени (t≥0) будут иметь коэффициент взаимной корреляции, равный 1, а эти же сигналы для отрицательного времени (t<0) будут иметь коэффициент взаимной корреляции, равный - 1. Поэтому результирующий коэффициент взаимной корреляции между этими сигналами на всей временной оси (|t|≤∞) будет равен нулю, что соответствует их ортогональности. Но поскольку исходный сигнал по определению является ограниченным во времени, то преобразование Гильберта, связывающее вещественную и мнимую части спектра, в данном случае будет справедливо только для бесконечной полосы частот. В реальных условиях полоса частот любого канала связи является ограниченной, в результате ограниченные по полосе одной и той же частотной функцией вещественная и мнимая части спектра исходного сигнала не будут точно и однозначно связаны преобразованием Гильберта. Действительно, в этом случае согласно преобразованию Гильберта для ограниченных по протяженности функций мнимая часть спектра при известной вещественной части Re(ω), которая является четной функцией частоты, определяется следующим выражением (Коржик В.И., Финк Л.М., Щелкунов К.Н. Расчет помехоустойчивости систем передачи дискретных сообщений (справочник). - М.: Радио и связь, 1981. - С.64):

где Δω и υ - соответственно эффективная полоса частот спектра сигнала и переменная интегрирования.

При этом ограниченная полосой частот Δω мнимая часть спектра исходного сигнала J_m(ω) не будет равна мнимой части спектра, определяемой выражением (1) .

Следовательно, и сигналы, соответствующие мнимой части ограниченного спектра исходного сигнала и мнимой части спектра, определяемого выражением (1), также будут различными по форме при одинаковых сигналах, соответствующих вещественным частям этих спектров. В этом случае коэффициент взаимной корреляции между сигналами, соответствующими вещественной и мнимой частям ограниченного по полосе спектра исходного сигнала, для физического (положительного) времени (t≥0) будет меньше единицы.

То, что в известном способе при передаче и приеме сигналов не учитывается это обстоятельство, является основным его недостатком, заключающимся в том, что в канал связи передается избыточный по структуре (частотно-временному ресурсу) сигнал.

Технический результат изобретения заключается в сокращении структурной (частотно-временной) избыточности передаваемого сигнала, что позволит повысить скрытность и сократить время передачи определенного количества информации в неизменной полосе частот.

Данный технический результат достигается за счет того, что по каналу связи передается сигнал, соответствующий только вещественной части ограниченного по полосе спектра исходного сигнала для физического (положительного) времени (t≥0). А сигнал, соответствующий мнимой части этого спектра, косвенно восстанавливается на приемной стороне по специальному корректирующему сигналу, передаваемому совместно с информационным сигналом на соответствующей временной позиции. Такая процедура исключает передачу в явном виде составляющую сигнала, соответствующую мнимой части ограниченного по полосе спектра, которая коррелированна с сигналом вещественной части и, следовательно, обладает частотно-временной избыточностью. А поскольку в соответствии с законом сохранения информации корректирующий сигнал должен переносить такое же количество информации, что и сигнал, соответствующий мнимой части спектра, и он некоррелирован с информационным сигналом, то, следовательно, он обладает меньшей частотно-временной избыточностью по сравнению с сигналом мнимой части спектра.

Сохранение передаваемой информации необходимо для того, чтобы по принятому информационному сигналу совместно с сигналом корректирующим можно было бы восстановить исходный сигнал, отображающий первоначальное сообщение.

При этом общий частотно-временной ресурс (ЧВР) (длительность сигнала и занимаемая им полоса частот) передаваемого информационного сигнала, соответствующего вещественной части спектра, и корректирующего сигнала для времени t≥0 будет меньше (по крайней мере, не будет превышать) частотно-временного ресурса исходного сигнала, ограниченного по полосе частот. Это проявляется в уменьшении эффективной длительности сигнала, соответствующего вещественной части спектра практически в неизменной полосе частот. При этом в той же полосе частот суммарная длительность сигнала вещественной части спектра и корректирующего сигнала будет меньше длительности исходного сигнала.

Для чего, как и в известном способе, после формирования исходного сигнала S₁(t), отображающего передаваемое сообщение, с соответствующим спектром S₁(jω)=S₁(ω)exp[-jϕ₁(ω)], ограниченным эффективной полосой частот Δω, где S₁(ω) и ϕ₁(ω) - амплитудный и фазовый спектры сигнала, формируют сигнал S_Re(t), соответствующий вещественной части спектра S_1Re(ω)=S₁(ω)cosϕ₁(ω) в той же полосе частот Δω. По каналу связи передают сигнал S₂(t)=S_Re(t) с точностью до постоянного множителя (коэффициента усиления), соответствующий положительному времени (t≥0) с ограниченной эффективной длительностью и обладающий спектром S₂(jω)=S₂(ω)exp[-jϕ₂(ω)], где S₂(ω) и ϕ₂(ω) - амплитудный и фазовый спектры передаваемого сигнала. Вместе с информационным сигналом на соответствующей временной позиции передают корректирующий сигнал S_кор(t), соответствующий весовой частотной функции P(ω)=S₁(ω)·S₂(0)/S₂(ω)·S₁(0). На приемной стороне по сигналу S₂(t) определяют его амплитудный спектр S₂(ω) и спектр, соответствующий его вещественной части S_2Re(ω)=S₂(ω)cosϕ₂(ω), а по корректирующему сигналу S_кор(t) определяют весовую частотную функцию Р(ω). Затем получают оценку амплитудного спектра и фазового спектра исходного сигнала на основе чего, пользуясь обратным преобразованием Фурье, получают оценку исходного сигнала

отображающего передаваемое сообщение.

Приведем пояснения отдельным понятиям и утверждениям. В частности, то, что для передачи используется сигнал, соответствующий вещественной части спектра, обусловлено тем, что этот спектр S_1Re(ω)=S₁(ω)cosϕ₁(ω) в большей степени сосредоточен в низкочастотной области, чем спектр мнимой части S_1Jm(ω)=S₁(ω)·sinϕ₁(ω), который является более высокочастотным и, следовательно, характеризует осциллирующую часть сигнала. Поэтому эффективная длительность сигнала вещественной части будет меньше (по крайней мере, не будет превышать) длительности сигнала мнимой части при одной и той же эффективной ширине этих спектров. В результате время на передачу сигнала, соответствующего вещественной части спектра, будет меньше времени на передачу сигнала, соответствующего мнимой части спектра. При этом под эффективной шириной спектра и эффективной длительностью сигнала понимается, соответственно, интервал частот и временной интервал, в которых сосредоточена основная доля энергии сигнала (Вакман Д.Е. Сложные сигналы и принцип неопределенности в радиолокации. - М.: Сов. Радио, 1965. - С.84).

Под исходным понимается видеочастотный сигнал, отображающий некоторое сообщение, который либо непосредственно может быть передан по физическому (проводному) каналу связи, либо с помощью известных методов модуляции и манипуляции может быть передан по радиоканалу связи.

Дополнительный множитель S₂(0)/S₁(0) для весовой частотной функции Р(ω) обусловлен тем, что на нулевой частоте (ω=0) значения спектров исходного сигнала, его вещественной части и передаваемого сигнала совпадают и, следовательно, для любых сигналов должно выполняться условие Р(0)=1. Это также означает, что наличие данного множителя исключает зависимость весовой частотной функции Р(ω) от коэффициента усиления передаваемого сигнала.

Особенностью предлагаемого способа является то, что вещественные части спектров исходного сигнала S₁(t) и передаваемого S₂(t) одинаковы:

Из условия (3) находится оценка фазового спектра исходного сигнала на приемной стороне:

При этом мнимые части спектров сигналов S₁(t) и S₂(t) в полосе частот Δω будут разными, что и обусловливает различие форм передаваемого и исходного сигналов в ограниченной полосе частот. Если бы полоса частот была неограниченной (равной бесконечности), тогда форма передаваемого сигнала точно бы повторяла форму исходного сигнала и никакого выигрыша в сокращении эффективной длительности передаваемого сигнала не было бы.

Но все реальные, физически реализуемые сигналы, как отмечалось ранее, имеют конечную протяженность по времени, следовательно, они обладают бесконечно протяженным по частоте спектром, который при передаче всегда ограничивается эффективной полосой частот, что и обусловливает сформулированный выше технический результат. При этом отмеченная в нем скрытность передачи информации обусловлена тем, что сигнал, передаваемый по каналу связи, отличается по форме от исходного сигнала, отображающего сообщение, для восстановления которого на приемной стороне необходимо выполнить ряд операций, которые неизвестны стороннему наблюдателю.

Приведем в общем виде доказательство того, что эффективная длительность сигнала, соответствующего вещественной части спектра, S_1Re(t) для t≥0, который подлежит передаче в ограниченной полосе частот, будет меньше (по крайней мере, не превышает) длительности исходного сигнала S₁(t).

Для чего запишем два неравенства Шварца-Буняковского одно для сигнала, определяемого вещественной частью спектра, а второе для исходного сигнала в полосе частот Δω, опустив при этом для обоих неравенств несущественный множитель 1/2π:

Первые интегралы в правых частях этих неравенств представляют собой энергию исходного сигнала в полосе частот Δω, которая является постоянной величиной и не зависит от текущего времени t и, следовательно, не влияет на конечный результат. Значение второго интеграла в правой части неравенства (5) будет меньше (не будет превышать) значения соответствующего интеграла в неравенстве (6), поскольку его подынтегральное выражение представляет собой произведение двух косинусов, каждый из которых по модулю не превышает единицы. Поэтому для каждого текущего момента времени t в некотором интервале (0, Т) правая часть неравенства (5) будет меньше правой части неравенства (6), следовательно, и значение интеграла в левой части неравенства (5) будет меньше соответствующего интеграла в неравенстве (6), откуда следует, что |S_1Re(t)|≤|S₁(t)|. А поскольку в начальный промежуток времени (для малых t≈0) из (5) и (6) следует, что |S_1Re(t)|≈|S₁(t)| и что энергия сигнала, соответствующего вещественной части спектра, меньше энергии исходного сигнала и полоса частот его ограничена, на основании этого можно заключить, что сигнал вещественной части спектра во времени убывает быстрее исходного сигнала. Отсюда следует, что эффективная длительность сигнала вещественной части спектра меньше длительности исходного сигнала, что и требовалось доказать.

В отличие от этого сигнал мнимой части спектра в начальный момент времени (t≈0) равен нулю, затем он будет возрастать и далее, в связи с его конечной энергией, будет убывать. Отсюда следует, что протяженность сигнала мнимой части спектра будет больше, чем сигнала вещественной части спектра. Именно поэтому для передачи по каналу связи принят сигнал, соответствующий вещественной части спектра.

Из выражений (5) и (6) также следует, что технический результат, заключающийся в сокращении структурной избыточности передаваемого сигнала, кроме амплитудного спектра S₁(ω), существенно зависит от фазового спектра ϕ₁(ω), характеризующего особенности структуры исходного сигнала. При этом из выражений (5) и (6) видно, что, главным образом фазовый спектр определяет частотно-временную избыточность сигнала. В частности, если сигнал простой, в том смысле, что его база B=ΔF_cT_c≈l, где ΔF_с и Т_c - соответственно полоса частот и длительность сигнала, то такой сигнал не обладает структурной избыточностью и, следовательно, для него предлагаемый способ передачи не обеспечивает выигрыша, указанного в техническом результате. В этом случае эффективная длительность сигнала вещественной части спектра будет практически равна длительности исходного сигнала.

Таким образом, указанный выигрыш проявляется только для сигналов, имеющих частотно-временную избыточность, у которых база В>1. Но практически все реальные сигналы, отображающие фрагменты передаваемых сообщений, обладают структурной избыточностью и, следовательно, при их передаче и приеме предлагаемым способом будет иметь место указанный технический результат. Причем возможны такие ситуации, когда исходные сигналы, имеющие одинаковые значения частотно-временной избыточности, обладают при данном способе передачи и приема разной эффективностью.

Таким образом, окончательный результат выигрыша, заключающийся в сокращении времени на передачу определенного количества информации в той же полосе частот, кроме частотно-временной избыточности, зависит от «тонких» структурных свойств сигналов, определяемых их амплитудными и фазовыми спектрами.

На примере конкретного исходного сигнала представим доказательство наличия указанного технического результата в предлагаемом способе.

Пусть исходный сигнал, подлежащий передаче, имеет вид убывающей по амплитуде синусоиды с частотой ω₁ и скоростью убывания, определяемой параметром α:

Такой сигнал выбран потому, что он обладает структурной (частотно-временной) избыточностью и удобен в последующих математических преобразованиях.

Вещественная часть спектра этого сигнала определяется известным выражением:

После подстановки (7) в (8) и представления синуса и косинуса соответствующими функциями комплексного аргумента, в результате решения интеграла (8), получим выражение вещественной части спектра, который имеет бесконечную протяженность по частоте:

Далее необходимо найти сигнал, соответствующий вещественной части спектра (9), но ограниченный по частоте. Для получения аналитического результата решение будем осуществлять в дискретном времени. Для чего ограничим ширину этого спектра интервалом Δω и разложим его в ряд Фурье на данном интервале как на периоде. При этом постоянная составляющая этого разложения, которая соответствует значению данного сигнала в момент t=0, в наших обозначениях определяется известным выражением (Харкевич А.А. Спектры и анализ. - М.: Физматгиз, 1962. - С.14):

Опуская промежуточные преобразования, решение интеграла (10) с учетом (9) будет иметь вид:

где ln(·) - знак натурального логарифма.

Поскольку для любого действительного сигнала вещественная часть его спектра является четной функцией частоты, то остальные составляющие (гармоники) разложения этого спектра в ряд Фурье будут определяться следующей формулой:

Составляющие a_n определяют также значения сигнала S_1Re(nt₀), соответствующие вещественной части спектра в моменты времени nt₀, где n=±1,±2,±3,..., а интервал дискретизации t₀ определяется в соответствии с теоремой Котельникова:

Для вычисления интеграла (12) необходимо воспользоваться следующим табличным интегралом (Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. - М.: Наука, 1971. - С.201):

где ci(u) и si(u) - соответственно интегральный косинус и интегральный синус, значения которых табулированы.

При подстановке (9) в (12) с учетом (14) и того, что подынтегральное выражение (12) является четной функцией частоты, решение данного интеграла получает следующий вид:

Для преобразования выражения (15) с целью получения коэффициентов разложения a_n в действительной форме, необходимо воспользоваться следующими свойствами интегрального синуса и косинуса:

где черта над z во второй строке означает комплексно-сопряженную величину.

С помощью свойств (16) и соответствующего разложения тригонометрических функций синуса и косинуса от комплексного аргумента совокупность 3, 4, 7, 8, 11, 12, 15, 16 слагаемых выражения (15) преобразуется к следующему виду:

При этом совокупность 1, 2, 5, 6, 9, 10, 13, 14 слагаемых выражения (15) с учетом известных разложений (Справочник по специальным функциям. Пер. с англ. / Под ред. М.Абрамовица, И.Стигана. - М.: Наука, 1979. - С.214) преобразуется к виду:

где функция g(z) представляется следующим асимптотическим разложением:

Аргументы этой функции в наших обозначениях имеют следующие значения:

Результирующее выражение для коэффициентов разложения будет равно

Ограничимся асимптотическим разложением (19) функции g(z) с точностью до четвертой степени, тогда с учетом (20) выражение (21) примет вид:

После соответствующих преобразований выражения (22), получим окончательную формулу для вычисления коэффициентов разложения вещественной части ограниченного спектра сигнала в ряд Фурье, которые соответствуют действительным значениям сигнала этого спектра в дискретные моменты времени:

Как и следовало ожидать функция а_n=S_1Re(nt₀) относительно n является четной, но для передачи реального сигнала S₂(nt₀), соответствующего положительному времени, необходимо использовать отсчеты только для n≥0, при этом a_n=S_1Re(nt₀)=S₂(nt₀).

Исходный сигнал (7) в дискретном времени запишется следующим образом:

По формулам (23) и (24) рассчитаны и сведены в таблицы 1 и 2 соответственно значения передаваемого сигнала S₂(nt₀) и исходного сигнала S₁(nt₀), умноженные на величину Δω, в дискретные моменты времени для n≥0 при следующих исходных данных: ω₁=2π (рад/мс); α=0,5 (1/мс); Δω=4ω₁=8π (рад/мс); t₀=2π/Δω=0,25 (мс).

Таблица 1Значения передаваемого сигнала, соответствующего вещественной части спектра, в дискретные моменты времени
n	0	1	2	3	4	5
an=S2(nt0)	1,096	1,077	0,065	-0,056	0,037	-0,025
Таблица 2Значения исходного сигнала в дискретные моменты времени
n	1	3	5	7	9	11	13	15	17	19	21	23	25	27
S1(nt0)	0,882	-0,687	0,535	-0,417	0,325	-0,253	0,197	-0,153	0,119	-0,093	0,072	-0,056	0,044	-0,034

Данные таблицы построены для таких значений n, при которых амплитуды последующих отсчетов сигналов не превышают 3% от амплитуды первого отсчета. Поэтому дальнейшее увеличение n и для первого (передаваемого) и второго (исходного) сигналов в данном примере нецелесообразно, поскольку связанное с этим увеличение длительности сигналов не окупается сколь-либо заметным улучшением точности их последующего восстановления.

В таблице 2 приведены значения исходного сигнала только для нечетных n, так как при указанных исходных данных для четных n эти значения равны нулю.

Из сравнительного анализа таблиц 1 и 2 следует, что сигнал S₂(nt₀) убывает значительно быстрее, чем сигнал S₁(nt₀), что свидетельствует о меньшей эффективной длительности передаваемого сигнала, соответствующего вещественной части спектра, по сравнению с исходным сигналом в одинаковой полосе частот Δω, что соответствует требованиям технического результата.

Для получения окончательного выигрыша в сокращении суммарной длительности передаваемого сигнала необходимо определить дополнительные временные затраты на передачу сигнала, отображающего корректирующую информацию. Для этого необходимо найти весовую частотную функцию Р(ω), подлежащую передаче. Первая составляющая этой функции - амплитудный спектр исходного сигнала, который определяется как модуль интеграла Фурье выражения (7), будет равен

Вторая составляющая весовой частотной функции - амплитудный спектр передаваемого сигнала, который при произвольном количестве временных отсчетов m будет равен

где а₀, а_n и t₀ определяются соответственно выражениями (11), (23) и (13).

Здесь мнимая часть спектра, которая определяется синусной составляющей подкоренного выражения (26), связана преобразованием Гильберта с вещественной частью спектра и отличается от мнимой части спектра исходного сигнала, а вещественные части спектров исходного и передаваемого сигналов одинаковы. Именно поэтому в данном способе форма передаваемого сигнала отличается от формы исходного сигнала.

При этом фазовый спектр передаваемого сигнала определяется выражением

В результате весовая частотная функция для m=5, больше которого спектр практически не меняется, с учетом (25) и (26) будет равна

Как и следовало ожидать на нулевой частоте Р(0)=1, так как на этой частоте спектры исходного и передаваемого сигналов совпадают.

Анализ выражения (28) свидетельствует, что Р(ω) является четной, медленно-меняющейся и возрастающей к границам полосы частот функцией, которую с высокой степенью точности можно аппроксимировать следующим выражением:

где γ и β - определяющие параметры функции.

Для всех физически реализуемых сигналов функция (29) имеет единственную точку ветвления ω=0, в которой она принимает значение Р(0)=1, а в зависимости от структуры сигнала будут соответствующим образом меняться ее определяющие параметры.

Для повышения точности аппроксимации Р(ω) можно выбрать более сложную структуру аппроксимирующей функции с большим количеством определяющих параметров, но только в том случае, если точность последующего восстановления исходного сигнала окупается соответствующим увеличением времени на передачу дополнительных определяющих параметров этой функции.

Важным здесь является то, что при изменении исходного сигнала S₁(t) сохраняется структурная устойчивость (вид) аппроксимирующей функции, а меняются только ее определяющие параметры. Это обусловлено тем, что амплитудные спектры S₁(ω) и S₂(ω), которые определяют функцию Р(ω), порождаются одним и тем же исходным сигналом S₁(t). Если меняется исходный сигнал, то S₁(ω) и S₂(ω) также меняются, но так, что вид весовой частотной функции Р(ω) остается неизменным, а меняются только ее определяющие параметры. Это подтверждается тем, что спектры S₁(ω) и S₂(ω) имеют одинаковые вещественные части, а мнимые части этих спектров разные, но обладающие одинаковой функциональной зависимостью от частоты, имеющей вид F(ω)=S(ω)sinϕ(ω), но с разными параметрами.

Действительно мнимые части этих спектров являются функциями нечетными, на частоте ω=0 они имеют нулевые значения, затем возрастают, достигая соответствующих максимумов, после чего убывают по причине конечной энергии, заключенной в этих частях спектров.

Таким образом, поскольку вещественные части спектров S₁(ω) и S₂(ω) одинаковы, а мнимые части этих спектров имеют функциональную структурную устойчивость, то следовательно, структурную устойчивость будет иметь и функция Р(ω) при изменении формы исходного сигнала S₁(t).

Для рассматриваемого примера исходного сигнала (7) и выбранных его параметрах α и ω₁ с учетом данных таблицы 1 определяющие параметры весовой частотной функции (29) имеют следующие значения: γ=0,82; β=0,13, которые должны быть переданы по каналу связи на соответствующих временных позициях. В результате для передачи всей информации в предлагаемом способе и в данном примере потребуется 7 отсчетов, из которых 5 на передачу основной информации и 2 на передачу корректирующей информации. При этом потребное время передачи составит 8t₀, так как на передачу последнего отсчета также потребуется время t₀.

В прототипе на передачу этой же информации (исходного сигнала) классическим способом потребуется 27 отсчетов (таблица 2), а время передачи составит 28 t₀. При этом максимальный выигрыш в сокращении времени передачи данного сигнала составляет η₁=28, t₀/8t₀=3,5 раза. Но при цифровой передаче исходного сигнала значения его четных отсчетов равны нулю (таблица 2), которые не передаются, поэтому время на передачу нечетных отсчетов в этом случае увеличивается в два раза. Следовательно, при одном и том же используемом коде длительность кодовых символов увеличатся в два раза, что соответствует сокращению занимаемой полосы частот в два раза. А это в свою очередь эквивалентно сокращению общего времени на передачу сигнала в два раза в той полосе частот, которая требуется в предлагаемом способе, так как в нем должны передаваться все отсчеты сигнала через время t₀. В итоге в данном примере окончательный выигрыш в сокращении суммарного времени передачи сигнала составит η₂=η₁/2=3,5/2=1,75 раза, что является также значительным результатом.

Анализ выражений (23) и (24) свидетельствует о том, что с увеличением параметра исходного сигнала α с одновременной коррекцией эффективной полосы частот Δω указанный выигрыш уменьшается и при значительных α>10 он практически становится равным нулю. Это объясняется тем, что с увеличением α исходный сигнал стремится к короткоимпульсной форме с базой В˜1, следовательно, его структурная избыточность и указанный выигрыш исчезают. Аналогичная ситуация имеет место в другом крайнем случае, когда α→0. В этом случае исходный сигнал приобретает вид монохроматического колебания, который, как известно, не имеет структурной избыточности и, соответственно, не обладает выигрышем в сокращении времени его передачи в неизменной полосе частот.

Таким образом, рассмотренный пример подтверждает сформулированное ранее положение о том, что данный выигрыш реализуется только для сигналов, обладающих структурной (частотно-временной) избыточностью. А все реальные сигналы или их отдельные фрагменты, отображающие передаваемые сообщения, как правило, обладают структурной избыточностью.

Следовательно, предлагаемый способ передачи и приема сигналов является практически применимым, реализует сформулированный технический результат и обладает, в связи с этим, повышенной эффективностью использования пропускной способности каналов связи.

Приведем сравнительный анализ качества восстановления исходного сигнала на приемной стороне в известном и предлагаемом способах обработки сигнала. При этом в качестве критерия будем использовать интеграл от квадрата модуля разности исходного и восстановленного сигналов (Вакман Д.Е., Седлецкий P.M. Вопросы синтеза радиолокационных сигналов. - М.: Сов. Радио, 1973. - С.31):

где S₁(t) и - соответственно исходный и восстановленный сигналы; E≈1/4α и T=28t₀ - соответственно энергия и длительность исходного сигнала; индекс к принимает значения 1 или 2 в зависимости от того каким способом (известным или предлагаемым) получен восстановленный сигнал.

Исходный сигнал, восстановленный классическим способом, в соответствии с известной теоремой Котельникова будет иметь вид

где L, t₀, S₁(nt₀) - соответственно количество отсчетов, интервал времени между отсчетами и значения отсчетов исходного сигнала.

В нашем случае L=14 (так как берутся только нечетные отсчеты), t₀=0,25 мс, а S₁(nt₀) для соответствующих n определяются по таблице 2.

С учетом этих данных и после подстановки выражений (7) и (31) в (30) и вычисления интеграла результат усредненного квадрата отклонения восстановленного сигнала от исходного составил величину .

Для восстановления исходного сигнала предлагаемым методом необходимо знать оценки его амплитудного и фазового спектров. Оценка амплитудного спектра исходного сигнала с учетом (26) и (29) определяется следующим образом:

Оценка фазового спектра исходного сигнала с учетом (4), (27) и (29) будет равна

В результате оценка исходного сигнала в соответствии с выражением (2) будет равна

Здесь Δω=4ω₁=8π рад/мс; t₀=0,25 мс; γ=0,82; β=0,13, которые определены ранее, а а₀ и a_n при m=5 и соответствующих n определяются из таблицы 1.

С учетом этих данных и после подстановки выражения (34) в (30) и численного решения соответствующего интеграла усредненный квадрат отклонения восстановленного сигнала от исходного составил , которое незначительно превышает . Это свидетельствует о том, что качество восстановления исходного сигнала в данном примере известным и предлагаемым способом практически одинаковое.

Таким образом, полученный выигрыш в сокращении времени на передачу сигнала в неизменной полосе частот, что соответствует сокращению его структурной избыточности при практически одинаковом качестве восстановления исходного сигнала на приемной стороне, свидетельствует о наличии причинно-следственной связи между совокупностью существенных признаков и достигаемым техническим результатом.

На фиг.1 представлена структурная функциональная схема системы, реализующая предлагаемый способ передачи и приема сигналов, а на фиг.2 - амплитудные спектры сигналов, поясняющие сущность предлагаемого способа.

Система (фиг.1) содержит в передающей части устройство 1 формирования амплитудного спектра S₁(ω) исходного сигнала в полосе частот Δω, устройство 2 формирования вещественной части спектра этого сигнала в той же полосе частот Δω, формирователь 3 сигнала S₂(t) для t≥0, подлежащего передаче по каналу связи,