Способ определения навигационных параметров бесплатформенной инерциальной навигационной системой

Способ определения навигационных параметров бесплатформенной инерциальной навигационной системой

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к области обработки данных в бесплатформенных инерциальных навигационных системах (БИНС).

Уровень техники

Одним из близких аналогов предлагаемого изобретения является описанный в патенте РФ №2272995 (2006) «Способ выработки навигационных параметров и вертикали места». Данный аналог не был выбран прототипом по причине практически полного применения указанного способа только к платформенным, а не к бесплатформенным системам. Единственным замечанием, касающимся бесплатформенных систем, в предлагаемом аналоге является фраза о том, что данная идея может быть реализована и в бесплатформенной технике, однако ничего конкретного и реального по этому применению приведено не было. Подтверждением этого также является материал автора этого изобретения в другой его отозванной заявке №2004129484 на изобретение «Способ выработки навигационных параметров и вертикали места бесплатформенной инерциальной системой», где под видом работы БИНС на самом деле описана работа двух конструктивно идентичных стабилизированных гироплатформ.

На самом деле реальные приложения способа выработки навигационных параметров в платформенном и бесплатформенном вариантах обладают существенной разницей. Самым важным недостатком указанного способа является то, что демпфирование гироплатформы осуществляют при условии отсутствия баллистических девиаций. Другими словами в динамическом движении (например, в различных маневрах летательного аппарата) предложенная коррекция не используется, в противном случае возникнет возмущаемость платформы, обусловленная ускорениями объекта. Отсюда, например, для грубых чувствительных элементов (дрейф гироскопа порядка 0,1 град/сек) в бесплатформенных системах этот способ вообще неприменим, поскольку за время выполнения маневра вычислительная платформа БИНС разойдется на большие углы по отношению к истинной навигационной.

Наиболее близким аналогом предлагаемого изобретения может считаться способ по патенту США №5422817 (1995), заключающийся в том, что сигналы акселерометров и гироскопов используются для вычисления углов ориентации путем расчета матрицы направляющих косинусов между связанной и навигационной системами координат. При этом происходит компенсация погрешностей сигналов ускорений акселерометров (американский термин «sculling»), обусловленная тем, что связанная система координат имеет угловую скорость по отношению к инерциальной системе. После чего происходит пересчет ускорений из связанной системы координат в навигационную систему и их интегрирование с целью определения текущих скоростей и приращений координат.

У указанного способа имеется традиционный недостаток любых инерциальных систем навигации, заключающийся в том, что ошибки в определении ориентации однозначно определяются точностью датчиков угловых скоростей (ДУС) и акселерометров, тогда как ошибки в определении координат растут с течением времени пропорционально скорости дрейфа ДУС. Этот недостаток особенно для относительно грубых чувствительных элементов (ДУС и акселерометров соответственно на уровне 0,1 град/сек и 10^-3 g) приводит к тому, что через некоторое время (это зависит от точности чувствительных элементов) автономной работы вычисленная на борту носителя навигационная система будет отличаться от истинной навигационной системы на большие углы, что фактически ведет к неработоспособности способа навигации. Ограниченность традиционного метода заключается в том, что ошибки инерциальной системы неотделимы от полезного сигнала (то есть истинных навигационных параметров). Этот вывод основан на том факте, что ошибки инерциальной системы имеют низкочастотный характер (так называемые шулеровские колебания), которые неотделимы от реальных движений носителя, на котором установлена система.

Надо заметить, что традиционный метод счисления навигационных параметров не зависит от параметров движения объекта, то есть точность системы (в первом приближении) не зависит от того, с какими параметрами двигается носитель, то есть совершает ли маневр или двигается с постоянной скоростью (крейсерский режим). Ошибки традиционного метода зависят исключительно от точности чувствительных элементов и никаким образом не корректируются внутренними связями. Раскрытие изобретения

Техническая задача заключается в существенном повышении точности счисления выходных навигационных параметров БИНС (углов ориентации, линейных скоростей и координат местоположения).

Технический результат достигается тем, что способ определения навигационных параметров БИНС основан на использовании сигналов блока акселерометров и гироскопических ДУС путем расчета матрицы направляющих косинусов между связанной и навигационной системами координат, компенсации погрешностей акселерометров за счет учета вращения связанной системы, пересчета показаний акселерометров из связанной в навигационную систему координат и их интегрирования для расчета текущих скоростей и приращений координат, и отличается тем, что производят параллельное вычисление совокупности матриц направляющих косинусов между связанной и навигационной системами координат по одним и тем же показаниям акселерометров и ДУС. Для каждой вычисленной матрицы направляющих косинусов определяют собственные навигационные параметры, имеющие различный частотный характер ошибок. При этом каждая из вычисленных матриц имеет индивидуальный закон управления (коррекции, демпфирования), и ошибки их вычисления также имеют различный частотный спектр в зависимости от режимов движения носителя, на котором установлена БИНС. Навигационные параметры для каждой вычисленной матрицы направляющих косинусов подают на входы блока мастер-фильтра, формирующего оптимальную комбинацию навигационных решений в зависимости от частотного диапазона их ошибок, а также от параметров движения носителя.

В отличие от известного способа счисления навигационных параметров одновременно рассчитывается не одна матрица направляющих косинусов между связанной и навигационной системой координат, а несколько. При этом расчет указанных матриц ведется параллельно по одним и тем же показаниям акселерометров и ДУС и каждая из вычисленных матриц имеет свой закон коррекции (демпфирования) ошибок, так что их ошибки имеют различный частотный спектр, зависящий как от параметров законов коррекции, так от параметров движения носителя, на котором установлена БИНС. По каждой из рассчитанных матриц производится определение собственных навигационных параметров. Навигационные параметры поступают далее на так называемый мастер-фильтр, который формирует оптимальную комбинацию навигационных решений за счет различного частотного спектра ошибок каждой из платформ и законов изменения углов ориентации и ускорений. Другими словами, в одном бортовом вычислителе реализуют не одну систему вычисления навигационных параметров, а совокупность систем, но при этом источник информации для них единый, т.е. основан на измерении только одного блока чувствительных элементов (акселерометров и ДУС). Мастер-фильтр имеет дело с совокупностью решений каждой из систем и формирует единое решение, являющееся оптимальным (наилучшим в среднеквадратическом смысле) для данного режима полета и всего частотного диапазона ошибок. Каждая из вычислительных платформ является возмущаемой в той или иной мере, но применение мастер-фильтра позволяет выбрать из частных решений общее, имеющее невозмущаемые части решений в своем составе.

Действительно, использование различного типа радиальных коррекций приводит к возмущаемости вычислительной платформы в маневрах и невозмущаемой части в крейсерском полете. Поскольку «быстрые маневры» имеют существенно малое время по сравнению с маломаневренным движением, то низкие частоты (когда объект не совершает маневра) являются невозмущаемыми, тогда как высокие частоты параметров ориентации возмущаемы за счет наличия существенных ускорений носителя. При использовании интегральной коррекции по показаниям выхода адаптивного фильтра Калмана система в маневрах является невозмущаемой, тогда как для слабоманевренного движения имеет существенные низкочастотные погрешности. Мастер-фильтр осуществляет разделение возмущаемой и невозмущаемой части решений каждой из вычислительных платформ и формирует общее решение, являющееся оптимальным (в среднеквадратическом смысле) для всего частотного диапазона изменения навигационных параметров.

В отличие от вышеупомянутого способа по патенту РФ №2272995 используют не разности одноименной информации, а их индивидуальные решения для каждой из всех вычислительных платформ, а их комбинации в мастер-фильтре объединяют как на основе частотных характеристик ошибок, так и на основе параметров движения носителя БИНС. Перечень чертежей

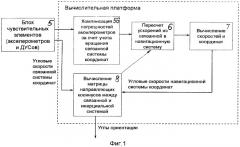
Фиг.1. Блок-схема традиционного способа вычисления навигационных параметров БИНС в обобщенном виде.

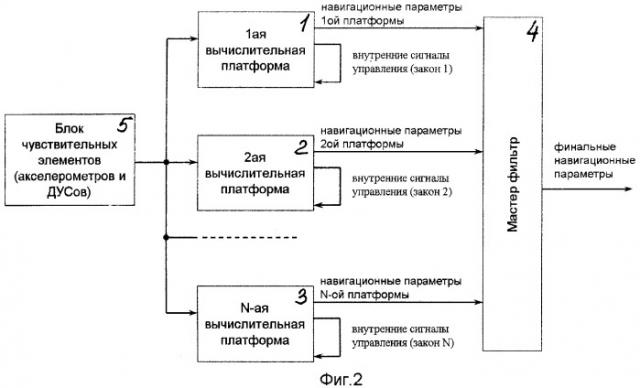
Фиг.2. Блок-схема предлагаемого способа вычисления навигационных параметров БИНС в обобщенном виде.

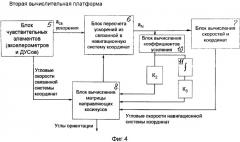
Фиг.3, 4, 5. Примеры блок-схем реализации трех вычислительных платформ в обобщенном виде.

Фиг.6. Пример блок-схемы реализации мастер-фильтра в обобщенном виде.

Фиг.7, 8, 9, 10. Сравнение частотных спектров угла тангажа по трем вычислительным платформам и с выхода мастер-фильтра, реализованным в малогабаритной БИНС «КомпаНав-2» на микромеханических гироскопах и акселерометрах, и эталонного спектра, полученного от высокоточной лазерной БИНС «И-42».

Фиг.11, 12. Сравнение показаний параметров тангажа и крена, полученных предлагаемым и традиционным способами, с аналогичными параметрами эталонной системы лазерной БИНС «И-42».

Осуществление изобретения

На Фиг.1...6 цифрами обозначены блоки в общем виде: блоки 1, 2, 3 вычислительных платформ, мастер-фильтр 4, блок 5 чувствительных элементов (акселерометров и ДУСов); блок 56 компенсации погрешностей акселерометров за счет учета вращения связанной системы координат («sculling»); блок 6 пересчета ускорений из связанной в навигационную систему координат; блок 7 вычисления скоростей и координат; блок 8 вычисления матрицы направляющих косинусов (между связанной и инерциальной системой); блок 9 вычисления коэффициента усиления K₁ первой вычислительной платформы; блок 10 вычисления коэффициентов усиления К₂, К₃ второй вычислительной платформы; блок интегрирования 11 интегральной ветви второй вычислительной платформы 2; адаптивный фильтр Калмана 12 третьей вычислительной платформы; фильтры Калмана ФК1 (13, 14) и ФК2 (15, 16) в схеме реализации мастер-фильтра 4 трех вычислительных платформ.

Традиционный и предлагаемый способы вычисления навигационных параметров БИНС представлены в обобщенном виде на Фиг.1 и 2.

В схеме вычислительной платформы традиционного способа сигналы акселерометров из блока 5 через блок 56 подают на блок 6, с которого сигналы поступают на блок 7. На блок 8 поступают сигналы угловых скоростей систем координат: связанной из блока 5 и навигационной из блока 7. Выходами блока 8 являются углы ориентации.

В традиционном способе после компенсации ошибок (блок 56) акселерометров (из блока 5), вызванных вращением связанной системы координат, происходит пересчет ускорений из связанной в навигационную систему (блок 6). При этом матрицу направляющих косинусов между связанной и навигационной системами координат (блок 8) рассчитывают (обычно через кватернионные преобразования) по угловым скоростям связанной и навигационной систем координат. При этом угловые скорости связанной системы непосредственно поступают из блока 5 чувствительных элементов датчиков, тогда как угловые скорости навигационной системы рассчитывают путем интегрирования ускорений навигационной системы (блок 7). Второе интегрирование указанных ускорений обеспечивает определение приращений координат (также блок 7).

Такой способ обладает традиционным недостатком, обусловленным зависимостью точности системы от погрешностей чувствительных элементов. При этом ошибки системы находятся на границе устойчивости, что недопустимо, особенно при использовании «грубых» чувствительных элементов. В предлагаемом способе параллельно реализуют несколько вычислительных схем (блоки платформ 1, 2, 3) определения навигационных параметров (по сигналам акселерометров и ДУСов блока 5). При этом каждая из вычислительных схем (или «вычислительных платформ») имеет свой закон управления, который с одной стороны обеспечивает устойчивость решения (без применения блока 56), но при этом является возмущаемым в зависимости от режима движения носителя. Чтобы снизить эффект возмущаемости необходимо выбирать параметры закона управления в зависимости от режима движения носителя (скорости изменения его курса, углов крена и ускорений). При этом каждый из законов управления обеспечивает свой частотный диапазон изменения ошибок навигационных параметров. Мастер-фильтр (блок 4) обеспечивает комбинацию навигационных решений, полученных с каждой из вычислительных платформ (1, 2, 3), на основе принципа частотного разделения индивидуальных решений, так что общее решение обеспечивает наилучшие показания системы во всем частотном диапазоне.

В зависимости от наборов конкретных блоков реализации предлагаемого способа возможно существенное повышение точности всех навигационных параметров (углов ориентации, скоростей, координат).

Пример осуществления способа

В примере рассматривается реализация способа, позволяющая повысить точность определения углов ориентации (тангажа, крена, курса).

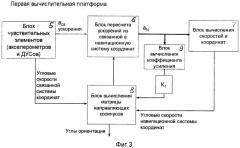
В качестве системы, реализующей предлагаемый способ, может быть использована инерциальная система, каждая из трех вычислительных платформ (1, 2, 3) которой имеет законы управления, показанные в обобщенном виде на Фиг.3, 4, 5. Нет блока 56 между блоками 5 и 6, но зато есть блоки реализации законов управления (коррекции) сигналов от блока 6 на блок 8.

На Фиг.3 представлена традиционная радиальная коррекция первой вычислительной платформы по сигналам акселерометров: К₁·а_x, K₁·a_y с переменным (через блок 9) коэффициентом К₁ (зависящим от параметров движения носителя), которые подают на вычислительную модель (так называемый «имидж») датчика момента гироплатформы (блок 8 вычисления матрицы направляющих косинусов). При этом при выборе жесткой обратной связи по ускорениям (большой коэффициент K₁) первая платформа будет иметь точные показания при крейсерском полете и иметь большие погрешности в маневрах (возмущаемость платформы по ускорениям). В частотном диапазоне эта платформа должна использоваться исключительно для низких частот изменения углов ориентации.

При выборе радиально-интегральной коррекции по ускорениям (вторая платформа, Фиг.4, блоки 10, 11) типа:

U₁=K₃·δV_y;

U₂=K₃·δV_x,

где

;

,

где U₁, U₂ - сигналы управления вычислительной платформы;

а_x, а_у - сигналы ускорений объекта в горизонтальной плоскости;

и при относительно малых величинах коэффициентов К₂ радиальной и K₃ интегральной (блок 11) ветвей вторая платформа будет обеспечивать наилучшие показания для средней частоты при малом маневрировании носителя.

В третьей платформе (Фиг.5) при использовании коррекции акселерометров через адаптивный фильтр Калмана (блок 12) с коэффициентом усиления К используют «слабое» управление (К порядка 1·10^-6) для демпфирования ошибок по выходным показаниям фильтра Калмана. При этом третья платформа обеспечивает высокие частоты при сильных маневрах летательного аппарата. В качестве измерений для адаптивного фильтра Калмана используют показания акселерометров в навигационной системе координат:

z_x=-gФ_x+a_x;

z_y=gФ_y+a_y,

где Ф_x, Ф_у - погрешности ориентации вычислительной платформы,

а_x, a_y - ускорения навигационной системы координат.

Адаптивный фильтр Калмана реализуют следующим образом:

;

;

P_K/K-1=ФР_K-1Ф^Т+GQG^T;

если >порога, R_K=S·R_ном.

K_K=P_K/K-1H^T[HP_K/K-1H^T+R_K]^-1;

P_K=(I-K_KH)·P_K/K-1,

где Ф - матрица перехода модели,

G - матрица входа,

- оценка вектора состояния (в данном случае - оценка ошибок ориентации Ф_x, Ф_у),

Р - ковариационная матрица ошибок оценивания,

Н - матрица измерений,

К_K - матрица усиления фильтра,

Q - ковариационная матрица входных шумов,

R_K - ковариационная матрица измерительных шумов,

S - коэффициент усиления матрицы шумов.

Отличие данного адаптивного фильтра Калмана от традиционного заключается в адаптивной подстройке матрицы измерительных шумов R_K в зависимости от квадрата величины обновляемого процесса, зависящего от реальных ошибок оценивания. Таким образом, задача фильтра Калмана - отфильтровать ускорения и оценить ошибки ориентации вычислительной платформы, что обеспечивает низкую степень возмущаемости БИНС в сильных маневрах.

Необходимо заметить, что коэффициенты К₁, К₂, К₃ не являются постоянными величинами, а зависят от параметров движения носителя, т.е. от режимов: сильный маневр; слабое маневрирование; крейсерское движение без маневрирования. Другими словами, реализуют математические функции коэффициентов K_i=f(γ, Н_ψ, а), где γ - крен, H_ψ - производная курса, а - ускорение носителя в плоскости горизонта. При этом уравнение ошибок ориентации имеет вид:

- для первой платформы;

- для второй платформы;

- для третьей платформы.

Здесь Ф_N,E - ошибки ориентации БИНС;

- дрейфы гироскопов;

а - ускорения носителя в плоскости горизонта;

- ошибки оценивания, допускаемые адаптивным фильтром Калмана.

Из приведенных уравнений следует, что при выборе различных значений коэффициентов К влияние дрейфа гироскопа будет различным (чем больше коэффициенты усиления в обратной связи, тем меньше влияние дрейфа гироскопов на ошибки ориентации).

Мастер-фильтр 4 осуществляет частотное разделение показаний всех трех платформ 1, 2, 3 и формирует выходные показания, являющиеся оптимальным решением для всего частотного диапазона и при различных движениях летательного аппарата. Частотное разделение сигналов базируется на оптимальной фильтрации (фильтр Калмана) показаний всех платформ, что более конкретно рассмотрено ниже.

Пример блок-схемы реализации мастер-фильтра 4 в обобщенном виде представлен на Фиг.6.

Схематично исходные сигналы трех платформ подают соответственно: 1-й - на блок 13 ФК1, 2-й - на блок 14 ФК1, 3-й - на блок 15 ФК2, а также указанные исходные сигналы 2-й и 3-й платформ также подают на два отдельные вычитающие устройства для соответствующего вычитания из них выходных сигналов блока 14 ФК1 и блока 15 ФК2. Выход первого указанного вычитателя далее суммируют с выходным сигналом блока 13 ФК1 и подают на блок 16 ФК2, выход которого суммируют с выходом второго указанного вычитателя.

Навигационные параметры, например углы ориентации, ϑ₁, ϑ₂ с первой и второй платформ поступают на фильтр Калмана (ФК1, блоки 13, 14). Данный фильтр Калмана в качестве модели полезного сигнала выбирает его низкочастотную составляющую. При этом все параметры фильтра Калмана (модель объекта и матрицы шумов) являются одинаковыми для первой и второй платформ. В результате на выходе этого фильтра имеются оценки , низкочастотной составляющей углов ориентации. При этом первая платформа обеспечивает точную оценку , тогда как низкочастотная составляющая второй платформы имеет уходы (за счет нежесткой обратной связи). После чего в показаниях второй платформы компенсируют неточную низкочастотную составляющую изаменяют в сигнале ϑ₂ точной составляющей . Таким образом, сигнал содержит низкочастотную составляющую с первой платформы, а средние и высокие частоты определяются второй платформой.

Аналогичные преобразования формируют для комбинации сигнала с измерениями от третьей платформы. При этом параметры фильтра Калмана (ФК2, блоки 15, 16) выбирают таким образом, чтобы его оценки содержали средние и низкие частоты сигнала.

После комбинации с оценками ФК2 с третьей платформы формируют сигнал ϑ^ф, который имеет оптимальные параметры для всего частотного диапазона (низкие, средние и высокие частоты).

Предлагаемый способ и система его реализующая применены в российской промышленно выпускаемой малогабаритной БИНС «КомпаНав-2» (ООО «ТеКнол») на микромеханических акселерометрах и гироскопах.

Производилось сравнение показаний одновременно работавших БИНС «КомпаНав-2» и эталонной лазерной БИНС «И-42» на носителе - самолете Як-18. Сравнение показывает, что предложенное решение по сравнению с традиционным обеспечивает критическое повышение точности. Данные испытаний системы официально подтверждены Актом Испытаний ЛИИ им. М.М.Громова (г.Жуковский, МО).

Для наглядного подтверждения на Фиг.7, 8, 9, 10 представлены частотные спектры измерений различных вычислительных платформ и с выхода мастер-фильтра в сравнении со спектром эталонного сигнала, полученных в реальных испытаниях «КомпаНав-2» на самолете Як-18. Из сравнения приведенных спектров очевидно, что первая платформа обеспечивает точные низкие частоты, вторая - средние, тогда как третья обеспечивает наиболее адекватные высокие частоты углов ориентации. Общий частотный спектр угла тангажа с выхода мастер-фильтра и частотный спектр выходного эталонного сигнала практически совпадают (см. Фиг.10).

Сравнение показаний временных реализации в реальных испытаниях параметров углов ориентации тангажа и крена такой системы по сравнению с традиционным исполнением и сигналами эталонной системы приведены на Фиг.11, 12. Предложенный способ улучшает точность счисления углов ориентации до 5-6 раз (в среднеквадратическом смысле) по сравнению с традиционным, что определяется разностью сигналов «КомпаНав-2» и эталона и традиционного способа и эталона.

Что касается повышения точности счисления параметров скоростей и координат, то возможно использовать аналогичные вычислительные платформы с аналогичными законами управления (коррекции, демпфирования) и аналогичным мастер-фильтром для дальнейшего повышения точности БИНС в части счисления скоростей и координат. Также коррекция ошибок ориентации в матрице направляющих косинусов автоматически приводит к повышению точности их счисления, то есть использование откорректированной по показаниям мастер-фильтра матрицы направляющих косинусов снижает погрешности в определении ускорений навигационной системы, а значит и скоростей и координат.

Способ определения навигационных параметров бесплатформенной инерциальной навигационной системой, основанный на использовании сигналов блока акселерометров и гироскопических датчиков угловых скоростей путем расчета матрицы направляющих косинусов между связанной и навигационной системами координат, компенсации погрешностей акселерометров за счет учета вращения связанной системы, пересчета показаний акселерометров из связанной в навигационную систему координат и их интегрирования для расчета текущих скоростей и приращений координат, отличающийся тем, что осуществляют разные режимы движения носителя, на котором установлена бесплатформенная инерциальная навигационная система, этими режимами являются сильный маневр, слабое маневрирование и крейсерское движение без маневрирования, при этом измеряют параметры движения носителя, этими параметрами являются крен, производная курса и ускорение носителя в плоскости горизонта, далее эти параметры используют для вычисления коэффициентов усиления систем, реализующих индивидуальные законы управления параллельно вычисляемых матриц направляющих косинусов между связанной и навигационной системами координат по одним и тем же показаниям акселерометров и датчиков угловых скоростей, для каждой вычисленной матрицы направляющих косинусов определяют собственные навигационные параметры, имеющие различный частотный характер ошибок, и ошибки вычисления каждой из матриц также имеют различный частотный спектр в зависимости от режимов движения носителя, навигационные параметры для каждой вычисленной матрицы направляющих косинусов подают на входы мастер-фильтра, формирующего оптимальную комбинацию навигационных решений в зависимости от частотного диапазона их ошибок, а также от параметров движения носителя.