Способ размещения элементов в фазированной антенной решетке (фар)

Способ размещения элементов в фазированной антенной решетке (фар)

Иллюстрации

Показать все

Реферат

Область техники

Изобретение относится к области антенной техники, а именно к способам размещения отдельных элементов по апертуре фазированной антенной решетки (ФАР).

Уровень техники

Традиционным способом размещения элементов в ФАР является регулярный, использующий свойство периодичности в декартовой (Д.М. Сазонов, Антенны и устройства СВЧ. - М.: Высш. шк., 1988, с.330) или цилиндрической системе координат (Антенные решетки. Методы расчета и проектирования. / Обзор зарубежных работ под ред. Л.С.Бененсона. - М.: Сов. Радио, 1966, с.238). Аналогом настоящего изобретения является кольцевое расположение элементов.

Ближайшим аналогом настоящего изобретения является способ размещения элементов по спиралям, составленным из дуг окружностей (Многоканальные антенные устройства с повышенной помехозащищенностью. / В.А. Балагуровский, А.С.Кондратьев, В.Н. Мосалов. // Радиотехника, 1993 г., №5-6, стр.53-58).

Сущность изобретения

В ближайшем аналоге элементы располагаются на спиралях, составленных из полуокружностей увеличивающего радиуса. Такой способ неудобен тем, что при последовательной запитке элементов, например через прямоугольный волновод, последний имеет ограничения на свою электрическую длину и, как следствие, на общее количество возбуждаемых элементов (в зависимости от частотного диапазона это число может меняться от 50 до 150).

Поскольку, как правило, в разрабатываемых ФАР общее количество элементов составляет несколько тысяч штук, необходимо иметь многозаходную квазикольцевую упаковку, универсальность которой обеспечивается тем, что количество заходов спирали определяется выбором числа элементов вдоль последовательного делителя и заданием общего количества элементов в ФАР.

Предлагаемый способ расположения элементов основан на построении спиралей из дуг окружностей, начиная с точек равномерного деления сторон правильного М-угольника на Р частей. На каждой спирали равномерно располагаются N отдельных элементов, например, в виде открытых концов круглого волновода. Сам М-угольник максимально плотно заполняется элементами, в частности при М=6, по гексагональной сетке. Координаты центров элементов на одной спирали на одной из сторон М-угольника, названной базовой, рассчитываются по следующему алгоритму:

x_ip=r_k·cos(ϕ_i+α)+r·cosϕ_k,

y_ip=r_k·sin(ϕ_i+α)+r·sinϕ_k,

где

i=1, 2 ..., N - номер элемента на спирали,

r_k=H·k-D·(p-1) - радиус дуги окружности с центром в k-й вершине М-угольника,

k=1, 2 ..., К - номер дуги окружности (одна и та же вершина может использоваться несколько раз, но с другим номером, поэтому К может быть больше М),

р=1, ..., Р - номер спирали на базовой стороне М-угольника,

r=H/[2·sin(π/M)],

Н - длина базовой стороны М-угольника,

D - расстояние между элементами вдоль спирали,

α=(2-М)·π/(2М),

ϕ_k=2πk/М,

ϕ_i=ϕ_i-1+δ_k для ϕ_i<ϕ_k,

при ϕ_i>ϕ_k осуществляется переход к следующей дуге, полагая k=k+1 и

ϕ_i=(ϕ_i-1-ϕ_k)[H·(k-1)-D·(p-1)]/[H·k-D·(p-1)]+ϕ_k+δ_k,

δ_k=2·arcsin(D/2r_k),

число дуг К определяется в соответствии с описанной процедурой из условия, что общее число элементов на каждой спирали равняется N, причем координаты остальных элементов определяются путем поворота координат элементов спиралей, начинающихся на базовой стороне, с учетом свойств симметрии

x_ipj=x_ip·cosβ-y_ip·sinβ,

y_ipj=x_ip·sinβ+y_ip·cosβ,

где

i - номер элемента в спирали,

р - номер спирали на базовой стороне М-угольника

j - номер стороны М-угольника,

β=2π(j-1)/M - угол поворота координат базовой стороны.

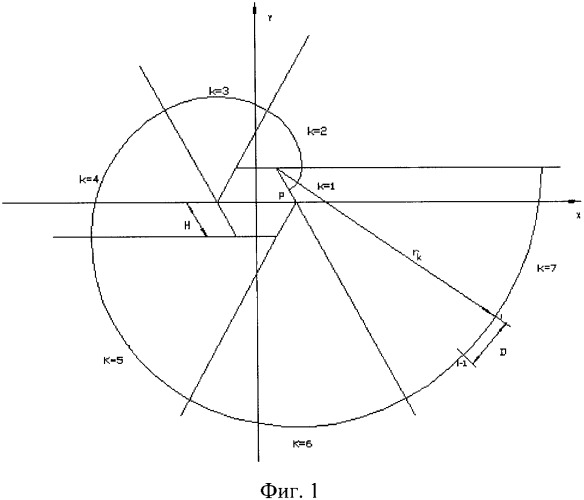
Схема построения геометрии отдельной спирали представлена на фиг.1.

Перечень чертежей

Фиг.1 - схема построения спирали из дуг окружностей, начинающихся на сторонах правильного шестиугольника.

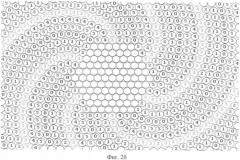
Фиг.2а - схема размещения элементов для М=6, Р=6 и N=50.

Фиг.2б - центральная часть схемы на фиг.2а.

Сведения, подтверждающие возможность осуществления изобретения

Приводится описание предпочтительной реализации, но при этом необходимо иметь в виду, что возможно внесение незначительных изменений без отклонения от рамок и духа настоящего изобретения.

Рассматриваемая реализация построена на основе шестиугольника (М=6), стороны которого разделены на 6 частей (Р=6), а из точек деления по рассмотренному алгоритму построены спирали, на каждой из них равномерно размещено 50 элементов с круглой апертурой (N=50). В общем случае параметры М, Р и N могут быть произвольными.

Схема плоской фазированной антенной решетки содержит

- Плоскую шестиугольную антенную решетку с гексагональной решеткой размещения элементов.

- Периферийную (основную) неэквидистантную спиральную решетку, составленную из спиралей, начинающихся на сторонах шестиугольника.

Полная схема плоской антенной решетки представлена на фиг.2, где на фиг.2а показана вся решетка, на фиг.2б - ее центральная часть.

По сравнению с прототипом предлагаемая структура антенной решетки обеспечивает более равномерное размещение элементов в центре и требует меньшей кривизны волноводов, подводящих питание к элементам.

Способ размещения элементов в фазированной антенной решетке (ФАР), содержащей элементы, размещенные по спиралям, составленным из дуг окружностей, отличающийся тем, что спирали начинаются из точек, равномерно расположенных на сторонах правильного М-угольника, а координаты центров элементов на одной спирали на одной из сторон М-угольника, названной базовой, рассчитываются по следующему алгоритму:

x_ip=r_k·cos(ϕ_i+α)+r·cosϕ_k,

y_ip=r_k·sin(ϕ_i+α)+r·sinϕ_k,

где i=1, 2 ..., N - номер элемента на спирали;

r_k=H·k-D·(p-1) - радиус дуги окружности с центром в k-ой вершине многоугольника;

k=1, 2 ..., К - номер дуги окружности (одна и та же вершина может использоваться несколько раз, но с другим номером, поэтому К может быть больше М);

р=1, ..., Р - номер спирали на базовой стороне М-угольника;

r=H/[2·sin(π/M)];

Н - длина стороны исходного М-угольника;

D - расстояние между элементами вдоль спирали;

α=(2-М)·π/(2М);

ϕ_k=2πk/М;

ϕ_i=ϕ_i-1+δ_k для ϕ_i<ϕ_k,

при ϕ_i>ϕ_k осуществляется переход к следующей дуге, полагая k=k+1

и

ϕ_i=(ϕ_i-1-ϕ_k)[Н·(k-1)-D·(р-1)]/[Н·k-D·(р-1)]+ϕ_k+δ_k,

δ_k=2·arcsin(D/2r_k),

число дуг К определяется в соответствии с описанной процедурой из условия, что общее число элементов на каждой спирали равняется N, причем координаты остальных элементов определяются путем поворота координат элементов спиралей, начинающихся на базовой стороне, с учетом свойств симметрии

x_ipj=x_ip·cosβ-y_ip·sinβ,

y_ipj=x_ip·sinβ+y_ip·cosβ,

где i - номер элемента в спирали;

р - номер спирали на базовой стороне М-угольника;

j - номер стороны М-угольника;

P=2π(j-1)/M - угол поворота координат базовой стороны.