Способ приема многокомпонентного сигнала в системе радиосвязи с n каналами передачи и м каналами приема (варианты) и устройство для его осуществления (варианты)

Способ приема многокомпонентного сигнала в системе радиосвязи с n каналами передачи и м каналами приема (варианты) и устройство для его осуществления (варианты)

Иллюстрации

Показать все

Реферат

Группа изобретений относится к области радиотехники, в частности к способу (варианты) и устройству (варианты) приема многокомпонентного сигнала в системе радиосвязи с N каналами передачи и М каналами приема, и может быть использована в системе связи с многомерными сигналами, например в системе связи MIMO.

Задача приема многокомпонентных сигналов возникает в большом числе областей телекоммуникаций, в том числе таких, как многопользовательское детектирование, прием с помощью адаптивных антенных решеток, технология Multiple-Input-Multiple-Output (MIMO), далее по тексту MIMO. Заявляемое изобретение будет описано на примере системы связи MIMO.

Технология MIMO привлекает большое внимание разработчиков и исследователей систем беспроводной связи, благодаря возможности значительного повышения пропускной способности.

В системах MIMO на передающей и приемной сторонах используется более одной антенны, вследствие чего пространственный канал связи между передатчиком и приемником имеет множество входов (multiple inputs) - каналов передачи сигнала, - и множество выходов (multiple outputs) - каналов приема сигнала. Всю совокупность каналов распространения сигнала между передающими и приемными антеннами принято называть каналом MIMO. Увеличение пропускной способности достигается за счет одновременной передачи различных информационных сигналов по различным пространственным подканалам канала MIMO.

Мгновенную реализацию канала MIMO оценивают на приемной стороне и используют при приеме сигнала. Использование данной оценки при передаче сигнала дает большое преимущество системе MIMO в плане возможности минимизировать уровень взаимных помех в точке приема. Метод MIMO, использующий оценку канала при передаче сигнала, называют MIMO с обратной связью (closed loop MIMO). Однако более практичным подходом является MIMO без обратной связи (open loop MIMO), когда оценка канала не доступна передающей стороне.

В системах MIMO без обратной связи из-за отсутствия информации о канале MIMO на передающей стороне нет возможности взаимно оптимизировать передачу информации по параллельным пространственным каналам, вследствие чего передаваемые через различные антенны сигналы создают взаимные помехи на приемной стороне. Наиболее распространенным способом передачи в системах MIMO без обратной связи является пространственное мультиплексирование (spatial multiplexing), впервые предложенное в рамках способа V-BLAST (см. G.J.Foshini, G.D.Golden, R.A.Valenzuela, "Simplified processing for high spectral efficiency wireless communication employing multi-element arrays," IEEE Selected Areas Communication, vol.17, pp.1841-1852, November,1999 [1], G.J. Foschini, G.D. Golden, "Wireless communications system having a space-time architecture employing multi-element antennas at both the transmitter and receiver (Patent style)," US patent: US 6317466 B1. Nov. 13, 2001 [2], G.J.Foschini, "Wireless communications system having a layered space-time architecture employing multi-element antennas," US Patent US#6097771, August 1, 2000 [3]).

Согласно способу пространственного мультиплексирования V-BLAST в передатчике выполняют кодирование, перемежение и модуляцию потока двоичных символов исходного информационного сообщения, формируя таким образом поток символов модуляции, каждый из которых представляет L последовательных бит исходного потока и принадлежит множеству m=2^L всевозможных значений.

Символы модуляции s обычно представляют комплексными числами, модуль и аргумент каждого из которых представляет собой амплитуду и, соответственно, фазу соответствующего символа модуляции. Действительная и мнимая часть данного комплексного числа являются квадратурными компонентами символа модуляции.

Сформированный поток символов модуляции разбивают на пакеты, каждый из которых состоит из N символов, где N - число передающих антенн. Из символов каждого пакета формируют радиосигналы, образуя соответствующий пакет информационных сигналов, который передают одновременно - по одному сигналу через каждую антенну.

Прием осуществляют с помощью M≥N приемных антенн. Сигнал каждой приемной антенны может быть представлен комплексным числом х, модуль которого соответствует амплитуде, а аргумент - фазе данного сигнала. Совокупность сигналов М приемных антенн обычно представляют М-мерным вектором комплексных чисел, который может быть выражен следующим образом

где х=[х₁,...х_M]^T - вектор принятых сигналов, s=[s₁,...s_N]^T - вектор символов модуляции, соответствующих передаваемому пакету информационных сигналов, Н - канальная матрица, каждый элемент h_i,j, которой представляет собой нормированный коэффициент передачи сигнала от j-й передающей к i-й приемной антенне, n=[n₁,...n_M]^T - вектор помех приемных антенн, которые обычно аппроксимируются, как независимые реализации аддитивного Гауссовского шума, [.]^T - знак транспонирования.

При приеме такого многомерного сигнала сначала выполняют оценку канальной матрицы Н, а затем с использованием этой оценки выполняют демодуляцию символов вектора s.

Наиболее эффективным алгоритмом приема многомерных сигналов является алгоритм максимального правдоподобия (maximum likelihood algorithm - MLA), представленный, например, в J.Jalden, Bjorn Ottersten, "On the Complexity of Sphere Decoding in Digital Communication," IEEE TRANSACTION ON SIGNAL PROCESSING, Vol.53, No. 4, pp.1474-1484, April; 2005 [4]. Оценкой максимального правдоподобия вектора передаваемых информационных символов s является значение, обеспечивающее минимум функционала отношения правдоподобия. Оценка переданного информационного пакета выражается как

где S - множество всевозможных значений вектора s. Следовательно, метод максимального правдоподобия предполагает поиск минимума решающей функции по множеству всевозможных значений вектора s. Сложность реализации данного метода зависит от объема множества поиска, который экспоненциально растет с увеличением количества передающих антенн и количества бит информации, передаваемых через каждую антенну. Поэтому даже при небольшом количестве передающих антенн алгоритм может оказаться весьма сложным при реализации в аппаратуре приемника.

С практической точки зрения весьма привлекательными являются линейные методы приема, при которых оценка вектора s символов модуляции формируется линейным преобразованием (см. D. Gesbert, "Robust linear MIMO receivers: A minimum error-rate approach," IEEE Trans. Signal Processing, Special issue on MIMO, May 2, 2003 [5]):

где (.)^t - символ транспонирования и комплексного сопряжения, W - матрица коэффициентов линейного преобразования, которую формируют таким образом, чтобы оптимизировать оценку в смысле некоторого критерия.

Наиболее эффективным из линейных методов является метод минимума среднеквадратичной ошибки оценки (minimum mean squared error - MMSE). При этом матрицу W формируют, как

где σ² - дисперсия шума в каждой из приемных антенн, I - диагональная единичная матрица размерности М×М, (.)^-1 - символ инверсии матрицы.

Известен также алгоритм, обеспечивающий нулевое значение ошибки в отсутствие шума. В зарубежных публикациях данный линейный алгоритм называют методом обращения в нуль - zero forcing. При этом матрица W формируется, как

Метод обращения в нуль обладает более низкой помехоустойчивостью, чем MMSE, но он проще в реализации, так как не требует оценки дисперсии шума.

По характеристикам помехоустойчивости метод минимума среднеквадратичной ошибки оценки проигрывает методу максимального правдоподобия. В канале MIMO с низкой обусловленностью матрицы Н этот проигрыш незначителен. Однако использование данным методом операции инверсии матрицы приводит к тому, что в канале MIMO с высокообусловленной канальной матрицей этот проигрыш увеличивается и становится весьма значительным.

Существенный прогресс в решении проблемы «плохой» обусловленности матрицы канала MIMO наметился при использовании подхода редукции базиса решетки (lattice basis reduction approach) (см. Dirk Wubben, Ronald Böhnke, Volker Kühn, and Karl-Dirk Kammeyer, "Near-Maximum-Likelihood Detection of MIMO Systems using MMSE-Based Lattice Reduction," IEEE Proc. International Conference on Communications (ICC), Paris, France, June 2004 [6], Christoph Windpassinger, Robert F.H. Fischer, "Low-Complexity Near-Maximum-Likelihood Detection and Precoding for MIMO Systems using Lattice Reduction," ITW2003, Paris, France, March 31-April 4, 2003 [7], Christoph Windpassinger, Robert F.H. Fischer, "From Lattice-Reduction-Aided Detection Towards Maximum-Likelihood Detection in MIMO Systems," IEEE Proc. Global Communications Con ference (GLOBECOM), Taipei, Taiwan, November 17-21 2002 [8], Huan Yao and Gregory W. Womell, "Lattice-Reduction-Aided Detectors for MIMO Communication Systems," in Proc. IEEE Globecom, Taipei, Taiwan, Nov., 2002 [9].

Идея данного подхода заключается в том, что канальную матрицу представляют в виде произведения хорошо обусловленной матрицы G и унимодулярной матрицы, то есть матрицы с целочисленными элементами и детерминантом ±1. Задачу демодуляции решают относительно модифицированного вектора переданных символов модуляции, который представляет собой произведение унимодулярной матрицы на исходный вектор s символов модуляции.

Демодуляцию выполняют в два этапа. На первом этапе выполняют субоптимальную демодуляцию модифицированного вектора символов с использованием хорошо обусловленной канальной матрицы G. Методы, основанные на инверсии матрицы, дают на этом этапе высокую помехоустойчивость, поскольку обращается хорошо обусловленная матрица. Полученную оценку модифицированного сигнала квантуют, за счет чего происходит фильтрация шума. На втором этапе выполняют преобразование оценки модифицированного сигнала в оценку исходного информационного сигнала с использованием унимодулярной матрицы.

Процедура разложения канальной матрицы на хорошо обусловленную и унимодулярную матрицы выполняется с помощью редукции базиса решетки (см. [6]-[9]). Соответственно, такой подход к демодуляции многомерного сигнала называют методом редукции базиса решетки или редукции решетки (lattice reduction). Именно данный подход лежит в основе заявляемого изобретения.

Реализация потенциально высокой пропускной способности систем MIMO возможна лишь с использованием эффективного помехоустойчивого кодирования. Поэтому еще одним важным аспектом при проектировании алгоритмов приема сигнала MIMO является то, что они должны хорошо сочетаться с алгоритмом помехоустойчивого кодирования.

Обычно в процессе приема сформированные оценки символов преобразуют в двоичную форму, и подают на декодер для восстановления двоичных символов исходного информационного сообщения. Наиболее эффективным декодированием является мягкое декодирование. При этом на вход декодера поступают мягкие оценки (решения) бит - в виде {В -В}, где знак соответствует жесткой оценке переданного двоичного символа (или бита) 1 или -1, а абсолютная величина В является метрикой, отражающей вероятностную меру принятия битом данного жесткого значения.

Метрикой мягкого декодирования (или мягким решением) некоторого бита b_k служит логарифм отношения правдоподобия (log-likelihood ratio - LLR). В отсутствие априорной информации о значениях переданных бит и при взаимной независимости передаваемых бит, логарифм отношения правдоподобия для k-го бита, переданного с помощью вектора s символов модуляции, может быть выражен, как показано в статье Dominik Seethaler, Gerald Matz, and Franz Hlawatsch, "Low-Complexity Soft Demodulation of MIMO-BICM Using the Line-Search Detector," Institute of Communications and Radio-Frequency Engineering, Vienna University of Technology. /0-7803-8939-5/05/ (С) 2005 IEEE [10]

где и - множества значений вектора s, для которых k-й бит принимает значение 1 и -1 соответственно, - норма вектора.

Формирование метрик (6) требует вычисления функции для всех элементов множеств и . Это значительно усложняет алгоритм приема, так как суммарное количество элементов данных множеств соответствует 2^LN и растет экспоненциально с увеличением числа передающих антенн N и L - количества бит, представляемых одним символом модуляции.

Линейные методы приема формируют мягкую (не квантованную) оценку каждого символа вектора s и допускают упрощенное формирование мягких решений, которое выполняют раздельно для каждого символа по полученной оценке данного символа и карте модуляции (см. Michael Мао Wang, Weimin Xiao, and Tyier Brown, "Soft Decision Metric Generation for QAM With Channel Estimation Error," IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 50, NO. 7, Pp.1058-1061, JULY 2002 [11]).

С использованием аппроксимации (см. [10]) можно записать следующее выражение для логарифма отношения правдоподобия k-го бита, передаваемого с помощью m-го модуляционного символа.

где - линейная оценка передаваемого символа модуляции s_m, and - множества значений символа модуляции s_m, для которого k-й бит принимает значение +1 и -1 соответственно, β_m - коэффициент преобразования символа s_m за счет канала связи и линейного преобразования, формирующего оценку (3).

Такой метод формирования мягких решений значительно проще, чем метод, основанный на выражении (6), однако он имеет и существенно более низкую помехоустойчивость.

Следовательно, другой серьезной проблемой приема сигнала MIMO, которая решается в способе заявляемого изобретения, является необходимость разработки эффективного алгоритма формирования мягких решений - метрик для мягкого декодирования.

Наиболее близким к заявляемому изобретению является техническое решение, описанное в [6].

Способ-прототип заключается в следующем.

Известный способ приема многокомпонентного сигнала в системе радиосвязи с N каналами передачи и М каналами приема (прототип), в котором

каждая из М компонент многокомпонентного сигнала, принимаемая по соответствующему ей каналу приема, представляет собой аддитивную смесь N информационных сигналов, каждый из которых передан по соответствующему ему каналу передачи, и помехи,

при этом каждый из N информационных сигналов соответствует L двоичным символам передаваемого информационного сообщения, принимает одно из m=2^L значений, соответствующих m символам модуляции, и

входит в каждую из М компонент многокомпонентного сигнала с весовым коэффициентом, отражающим коэффициент передачи пространственного канала, образованного каналом передачи этого информационного сигнала и каналом приема данной компоненты многокомпонентного сигнала, причем считают, что коэффициенты передачи пространственных каналов и значения дисперсии помех М каналов приема известны или предварительно оценены, заключается в том, что

формируют вектор принимаемого сигнала, таким образом, что

принимают каждую из М компонент сигнала, определяя для каждой из них комплексное число х, модуль которого отражает амплитуду, а аргумент - фазу данной компоненты многокомпонентного сигнала, формируя из данных комплексных чисел М-мерный комплексный вектор х принятого сигнала, и преобразуют данный вектор к вектору принятого сигнала по формуле

формируют канальную матрицу используя коэффициенты передачи пространственных каналов, таким образом, что между вектором принимаемого многокомпонентного сигнала и сформированной канальной матрицей выполняется соотношение

где - вектор символов модуляции, соответствующих N информационным сигналам, - вектор помех М каналов приема,

с этой целью из коэффициентов h_i,j, передачи пространственных каналов, каждый из которых представляет собой комплексное число, с модулем и аргументом, отражающими изменение соответственно амплитуды и фазы j-го информационного сигнала, принимаемого в i-м канале приема, при его распространении по соответствующему пространственному каналу, формируют комплексную канальную матрицу Н, которую преобразуют в матрицу Н_r по формуле

где ReH и ImH - матрицы соответственно действительных и мнимых частей элементов матрицы Н, матрицу Н_r расширяют, дополняя снизу матрицей σI, где σ² - дисперсия помехи каждого из М каналов приема, I - единичная диагональная матрица размерности 2N×2N

формируя, таким образом, канальную матрицу

преобразуют канальную матрицу в матрицу G, характеризующуюся заведомо низким числом обусловленности, для чего

путем редукции базиса решетки матрицы формируют целочисленную матрицу Т с определителем, равным ±1, и формируют модифицированную канальную матрицу G, как произведение

определяют вектор z модифицированных символов модуляции как вектор символов модуляции умноженный слева на инверсию матрицы Т, то есть и оценивают его, используя канальную матрицу G и вектор принимаемого сигнала, формируя таким образом вектор оценок модифицированных символов модуляции по формуле

где (.)', (.)^-1 символы транспонирования и инверсии матрицы, соответственно, - вектор принимаемого сигнала, расширенный снизу 2М-мерным вектором нулей 0;

квантуют вектор оценок модифицированных символов 5 модуляции, определяя для каждого элемента данного вектора квантованное значение, как модифицированный символ модуляции, обеспечивающий наименьшую ошибку квантования, и формируют таким образом вектор u, элементы которого являются квантованными оценками модифицированных символов модуляции;

преобразуют вектор u, умножая слева на матрицу Т

формируя таким образом вектор r, элементы которого являются действительными оценками символов модуляции, соответствующих N передаваемым информационным сигналам;

используя вектор r, формируют вектор оценок символов модуляции, соответствующих N передаваемым информационным сигналам, по формуле

где r1, r2 - N-мерные векторы, составленные из первой и второй половины элементов вектора r соответственно, - мнимая единица, и,

используя вектор принимают решение о передаваемом информационном сообщении.

Реализация способа-прототипа представлена в статье [6] на примере системы связи MIMO, структурная схема которой выполнена на фиг.1.

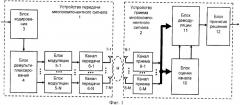
Система связи (MIMO) в соответствии с фиг.1 содержит устройство 1 передачи многокомпонентного сигнала (передатчик) и устройство 2 приема многокомпонентного сигнала (приемник). При этом устройство 1 передачи многокомпонентного сигнала содержит блок 3 кодирования, блок 4 демультиплексирования, N блоков 5-1 - 5-N модуляции, N каналов 6-1 - 6-N передачи многокомпонентного сигнала и соответственно N передающих антенн 7-1 - 7-N. Устройство 2 приема многокомпонентного сигнала содержит М антенн 8-1 - 8-М для приема многокомпонентного сигнала, соответственно М каналов 9-1 - 9-М приема, блок оценки канала, блок 11 демодуляции и блок 12 принятия решения.

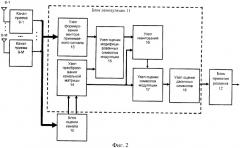
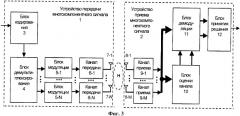
Прототипом для заявляемого устройства является устройство приема многокомпонентного сигнала в системе радиосвязи (MIMO), структурная схема которого выполнена на фиг.2, на нем реализуют способ-прототип.

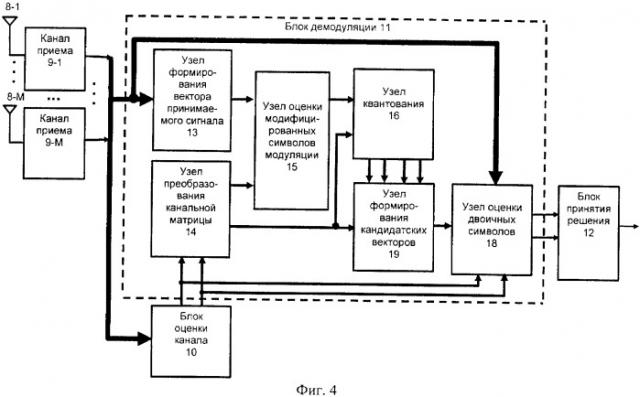
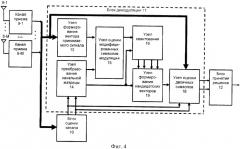
Устройство-прототип (фиг.2) содержит М антенн 8 - 1-8-М для приема многокомпонентного сигнала, соответственно, М каналов 9-1-9-М приема, блок 10 оценки канала, блок 11 демодуляции и блок 12 принятия решения, при этом выходы М антенн 8-1 - 8-М для приема многокомпонентного сигнала соединены соответственно с входами М каналов 9-1 - 9-М приема, выходы которых соединены через шину данных с входом блока 10 оценки канала и первым входом блока 11 демодуляции, вход блока оценки канала и первый вход блока демодуляции являются сигнальными входами, второй и третий входы блока демодуляции соединены соответственно с первым и вторым выходами блока 10 оценки канала, формирующего на первом выходе оценки комплексных коэффициентов передачи сигнала при распространении от каждой из передающих к каждой из приемных антенн, а на втором выходе - оценки значений дисперсии шума каналов приема, выход 11 блока демодуляции соединен со входом блока 12 принятия решения, выход которого является выходом устройства, блок 11 демодуляции содержит узел 13 формирования вектора принимаемого сигнала, узел 14 преобразования канальной матрицы, узел 15 оценки модифицированных символов модуляции, узел 16 квантования, узел 17 оценки символов модуляции и узел 18 оценки двоичных символов, при этом вход узла 13 формирования вектора принимаемого сигнала является первым входом блока 11 демодуляции, первый и второй входы узла 14 преобразования канальной матрицы являются соответственно вторым и третьим входами блока 11 демодуляции, выход узла 13 формирования вектора принимаемого сигнала соединен с первым входом узла 15 оценки модифицированных символов модуляции, второй вход которого соединен с первым выходом узла 14 преобразования канальной матрицы, выход узла 15 оценки модифицированных символов модуляции соединен с первым входом узла 16 квантования, второй вход которого объединен с первым входом узла 17 оценки символов модуляции и соединен со вторым выходом узла 14 преобразования канальной матрицы, второй вход узла 17 оценки символов модуляции соединен с выходом узла 16 квантования, выход узла 17 оценки символов модуляции соединен с входом узла 18 оценки двоичных символов, выход которого является выходом блока 11 демодуляции.

Осуществляют способ-прототип на устройстве (фиг.2) следующим образом.

В устройстве приема многокомпонентного сигнала принимают входной сигнал посредством М антенн 8-1 - 8-М, выход каждой из которых соединен с входом соответствующего канала 9-1 - 9-М приема.

В каждом из М каналов 9-1 - 9-М приема выполняют функции обработки сигнала на радиочастоте, синхронизации, а также перенос в область видеочастоты и преобразование в цифровую форму.

На выходе каждого из М каналов 9-1 - 9-М приема формируется принимаемый сигнал, как комплексное число, модуль которого отражает амплитуду, а аргумент - фазу данного сигнала.

В процессе дальнейшей обработки сигнала совокупность принимаемых сигналов М каналов 9-1 - 9-М приема рассматривается, как М-мерный комплексный вектор принимаемого сигнала x=[x₁,...x_N]^T.

Сформированный таким образом вектор х принимаемого сигнала поступает (по шине) на сигнальные входы - первый вход блока 11 демодуляции и вход блока 10 оценки канала.

В блоке 10 оценки канала выполняют оценку канальной матрицы Н и оценку дисперсии шума каналов приема σ². На первом выходе блок 10 оценки канала формирует оценки комплексных коэффициентов передачи сигнала при распространении от каждой из передающих к каждой из приемных антенн, а на втором выходе - оценки значений дисперсии шума каналов приема.

Выходные сигналы с первого и второго выходов блока 10 оценки канала поступают соответственно на второй и третий входы блока 11 демодуляции.

С первого входа блока 11 демодуляции сигнал поступает на входы узла 13 формирования вектора принимаемого сигнала. Со второго входа блока демодуляции сигнал поступает на первый вход узла 14 преобразования канальной матрицы. С третьего входа блока 11 демодуляции сигнал поступает на второй вход узла 14 преобразования канальной матрицы.

В узле 13 формирования вектора принимаемого сигнала М-мерный вектор x преобразуется к 2М-мерному действительному вектору в соответствии с формулой (8).

В узле 14 преобразования канальной матрицы комплексно-значную канальную матрицу Н преобразуют к реально-значной матрице Н_r по формуле

где ReH и ImH - матрицы, соответственно, действительных и мнимых частей элементов матрицы Н, матрицу Н_r расширяют, дополняя снизу матрицей σI,

где σ² - дисперсия помехи каждого из М каналов приема, I - единичная диагональная матрица размерности 2N×2N, формируя таким образом канальную матрицу .

По матрице формируют матрицу Т редукции базиса решетки. При этом используют, например, известный алгоритм Lenstra-Lenstra-Lovasz (LLL) (см. [6] и А.К. Lenstra, H.W. Lenstra, and L. Lovasz, "Factoring polynomials with rational coefficients," Mathematische Annalen, vol.261, pp.515-534, 1982 [12]). С использованием матриц и Т формируют модифицированную канальную матрицу .

В узле 15 оценки модифицированных символов модуляции, на первый вход которого с выхода узла 13 формирования вектора принимаемого сигнала поступает вектор принимаемого сигнала, а на второй его вход с первого выхода узла 14 преобразования канальной 5 матрицы поступает модифицированная канальная матрица G, формируют вектор оценок модифицированных символов модуляции. При этом используют, например, формулу (12).

Сформированный вектор оценок модифицированных символов модуляции с выхода узла 15 оценки модифицированных символов модуляции поступает на первый вход узла 16 квантования, в котором выполняют квантование вектора оценок модифицированных символов модуляции. При этом по матрице Т редукции базиса решетки и символам выбранного вида модуляции определяют модифицированные символы модуляции. Для каждого элемента вектора определяют квантованное значение как модифицированный символ модуляции, обеспечивающий наименьшую ошибку квантования, и формируют, таким образом, вектор u, элементами которого являются квантованные оценки модифицированных символов модуляции. Ошибку квантования определяют, например, как абсолютную величину разности между квантованным и не квантованным значением оценки.

Сформированный вектор u с выхода узла 16 квантования поступает на второй вход узла 17 оценки символов модуляции, в котором формируют вектор оценок символов модуляции, для чего вектор u преобразуют в вектор r действительных оценок модифицированных символов модуляции по формуле r=Tu. А затем, используя вектор r, формируют вектор оценок символов модуляции, соответствующих N передаваемым информационным сигналам, по формуле где r1, r2 - N-мерные векторы, составленные из первой и второй половины элементов вектора r соответственно, - мнимая единица.

Вектор оценок символов модуляции с выхода узла 17 оценки символов модуляции поступает на вход узла 18 оценки двоичных символов. В узле 18 оценки двоичных символов формируется последовательность двоичных символов, соответствующих вектору . Полученная последовательность двоичных символов поступает на выход 11 блока демодуляции, а с выхода блока 11 демодуляции на вход блока 12 принятия решения. В блоке 12 принимают решение, например, путем декодирования последовательности двоичных символов. Выходной сигнал с блока 12 принятия решения поступает на выход устройства.

Описанный способ-прототип и устройство для его осуществления используют линейный метод детектирования сигнала в совокупности с редукцией базиса решетки канальной матрицы. Методика редукции базиса решетки позволяет снизить обусловленность канальной матрицы и, вследствие этого, получить улучшение характеристик помехоустойчивости относительно исходного субоптимального линейного метода. Однако данное улучшение наблюдается в диапазоне относительно высоких значений отношения сигнал-шум (ОСШ). Вместе с тем, способ-прототип и устройство для его осуществления все-таки существенно уступают по помехоустойчивости методу максимального правдоподобия, а в области низких значений ОСШ они проигрывает также и исходному линейному методу.

Данный факт объясняется тем, что важной операцией данного подхода является квантование, цель которого отфильтровать шум оценки перед выполнением преобразования, обратного редукции базиса решетки. Однако квантование, являясь нелинейной операцией, эффективно лишь тогда, когда шумовые отклонения невелики. В области же высокого относительного уровня шума квантование приводит к ошибкам детектирования и характеристики приема ухудшаются.

Другим существенным недостатком способа-прототипа и устройства для его осуществления является низкая эффективность при использовании мягкого декодирования. Мягкое декодирование предполагает получение информации, как о значениях двоичных символов информационного сообщения, так и о надежности оценки данных значений. Квантование приводит к формированию жестких - квантованных оценок, из которых достаточно трудно извлечь информацию о надежности оценки. Вследствие этого при мягком декодировании проигрыш способа- и устройства-прототипа относительно оптимального метода увеличивается.

Задача изобретения - повышение помехоустойчивости приема многокомпонентного сигнала, как в системе радиосвязи без кодирования, так и в системе радиосвязи с кодированием при мягком и жестком декодировании.

Задача решается заявляемыми способом приема многокомпонентного сигнала в системе радиосвязи с N каналами передачи и М каналами приема (варианты) и устройством для его осуществления (варианты), алгоритм которых разработан с приемлемой для практики сложностью реализации и высокой помехоустойчивостью приема, как в системах связи без кодирования, так и в системах связи с кодированием при мягком и жестком декодировании.

Задача решается разработкой заявляемого способа приема многокомпонентного сигнала в системе радиосвязи с N каналами передачи и М каналами приема по первому варианту реализации, в котором

каждая из М компонент многокомпонентного сигнала, принимаемая по соответствующему ей каналу приема, представляет собой аддитивную смесь N информационных сигналов, каждый из которых передан по соответствующему ему каналу передачи, и помехи,

при этом каждый из N информационных сигналов соответствует L двоичным символам переданного информационного сообщения, принимает одно из m=2^L значений, соответствующих m символам выбранного вида модуляции, и входит в каждую из М компонент многокомпонентного сигнала с весовым коэффициентом, отражающим коэффициент передачи пространственного канала, образованного каналом передачи этого информационного сигнала и каналом приема данной компоненты многокомпонентного сигнала, причем считают, что коэффициенты передачи пространственных каналов и значения дисперсии помех М каналов приема известны или предварительно оценены, заключающийся в том, что

формируют вектор принимаемого многокомпонентного сигнала;

формируют канальную матрицу используя коэффициенты передачи пространственных каналов, таким образом, что между вектором принимаемого многокомпонентного сигнала и канальной матрицей выполняется соотношение

где - вектор символов модуляции, соответствующих N информационным сигналам,

- вектор помех М каналов приема;

преобразуют канальную матрицу в матрицу G, характеризующуюся заведомо низким числом обусловленности, для чего

путем редукции базиса решетки матрицы формируют целочисленную матрицу Т с определителем, равным ±1, и формируют модифицированную канальную матрицу G, как произведение

определяют вектор z модифицированных символов модуляции как и оценивают его, используя канальную матрицу G и вектор принимаемого сигнала, формируя таким образом вектор оценок модифицированных символов модуляции,

используя вектор оценок модифицированных символов модуляции и матрицу Т, формируют К кандидатских векторов, каждый из которых представляет собой совокупность оценок N символов модуляции, соответствующих N переданным информационным сигналам, где К≤m^N,

для чего

выполняют квантование вектора оценок модифицированных символов модуляции, определяя для каждого элемента этого вектора квантованные значения, как модифицированные символы модуляции, формируя из этих квантованных значений векторы u, каждый из которых представляет собой совокупность квантованных оценок модифицированных символов модуляции, и определяют К векторов u с наименьшими значениями погрешности квантования,

каждый из К векторов u умножают слева на матрицу Т, формируя вектор r

r=Tu,

элементы полученных векторов r, которые не принадлежат множеству всевозможных значений квадратурных компонент символов выбранного вида модуляции, заменяют наиболее близким по величине значением из данного множества,

формируя, таким образом, К действительных кандидатских векторов r;

каждый из сформированных К действительных кандидатских векторов преобразуют в кандидатский вектор по формуле

v=r1+j·r2,

где r1, r2 - N-мерные векторы, составленные из первой и второй половины элементов кандидатского вектора r соответственно, - мнимая единица.

используя К сформированных кандидатских векторов, оценивают последовательность двоичных символов, и по результатам оценки принимают решение о переданном информационном сообщении.

Задача также решается заявляемым способом приема многокомпонентного сигнала в системе радиосвязи с N каналами передачи и М каналами приема по второму варианту реализации, в котором

каждая из М компонент многокомпонентного сигнала, принимаемая по соответствующему ей каналу приема, представляет собой аддитивную смесь N информационных сигналов, каждый из которых передан по соответствующему ему каналу передачи, и помехи,

при этом каждый из N информационных сигналов соответствует L двоичным символам переданного информационного сообщения, принимает одно из m=2^L